Developing EPQ models for non-instantaneous deteriorating items

Abstract

In this paper, the classical economic production quantity (EPQ) model is developed for non-instantaneous deteriorating items by considering a relationship between the holding cost and the ordering cycle length. Two models are developed. First, the proposed model is considered when backorders are not permitted and this condition is waived for the second case. The cost functions associated with these models are proved to be convex and an algorithm is designed to find the optimum solutions of the proposed model. Results show that the relationship between holding cost and ordering cycle length has a significant impact on the optimal lot size and total cost in the EPQ model. Numerical examples are presented to demonstrate the utility of the models.

Introduction

In recent years, inventory problems for deteriorating items have been widely studied. In general, deterioration is defined as the damage, spoilage, dryness, vaporization, etc., which decrease of usefulness of the commodity. One of the important problems in inventory management is how to control and maintain the inventories of deteriorating items such as food items, pharmaceuticals, chemicals, and blood. Analysis of inventory system is usually carried out without considering the effects of deterioration; however, there are items such as highly volatile substances, radioactive materials, etc., in which the rate of deterioration should not be ignored (Valliathal and Uthayakumar 2011). Some researchers assume that the deterioration of the items in inventory starts from the instant of their arrival; however, many goods maintain freshness or original condition for a period of time. During this period deterioration would not take place. This phenomenon is defined as non-instantaneous deterioration.

Furthermore, in classical EPQ models the parameters like setup cost, holding cost and also the rate of demand are fixed. This is why the results of classical models have some differences compared with real-world conditions. Therefore, some practitioners and researchers have questioned practical applications of classical EPQ models due to several unrealistic assumptions (Jaber et al. 2004). This deficiency has motivated many researchers to modify the EPQ model to match real-life situations and this paper represents some real-life situations in which the holding cost can be taken into account for increasing the function of ordering cycle length. This is particularly true in the storage of non-instantaneous deteriorating and perishable items such as food products. The longer these food products are kept in storage, the more sophisticated the storage facilities and services needed and, therefore, the higher the holding cost. Deterioration is defined as decay, spoilage, loss of utility of the product and this process is observed in volatile liquids, beverages, medicines, blood components, food stuffs, dairy items, etc. Therefore, it is reasonable and realistic to consider holding cost as time dependent for deteriorating and non-instantaneous deteriorating items.

In this paper, EPQ models for non-instantaneous deteriorating items in which holding cost is an increasing function of the ordering run length are developed. The classical EPQ model is extended by considering a relationship between holding cost and the ordering cycle length. In practical real-life situations, most of the goods would have a period of maintaining quality or preserving original condition, during which (e.g., electronic goods, blood banks, fresh fruits, and so on) no deterioration occurs. Since deterioration does not occur, it is assumed that holding cost is constant. However, when deterioration starts, extra effort and more capital investment in storehouse equipment is needed to overcome it, therefore, here, it is considered that holding cost is increasing as function of the ordering cycle length. The economic ordering cycle length and the economic ordering quantity are obtained. Two models are developed that consider the cases of with and without shortages in which shortage occurs and in the other one it does not happen. Optimal solutions are derived and convexity of the cost functions is established. Besides, numerical examples are given to test and verify the theoretical results.

The rest of the paper is organized as follows: In Sect. “Literature review”, a brief literature review has been presented. In Sect. “Assumptions and notation”, the assumptions and notations which are used throughout the paper are presented. In Sect. “Models development”, mathematical models are formulated, an algorithm to find the optimal solution is carried out and numerical examples are provided to illustrate the theory. Finally, conclusions and future research topics are presented in Sect. “Conclusions and suggestions”.

Literature review

Since the economic production quantity (EPQ) model was introduced, some researchers have investigated and questioned the practical usages of this model due to the unrealistic assumptions regarding model input parameters, which are the setup cost, holding cost and demand rate (Jaber et al. 2004). The classical EPQ model has been investigated in many ways, for example Huang (2004) investigated the optimal replenishment policy under conditions of permissible delay in payments within an EPQ framework. Salameh and Jaber (2000) extended the traditional EPQ/EOQ model by accounting for imperfect quality items when using the EPQ/EOQ formulae. They also considered the issue that poor-quality items are sold as a single batch by the end of the 100 % screening process. Jaber et al. (2004) applied first and second laws of thermodynamics on inventory management problem. They showed that their approach yields higher profit than that of the classical EPQ model. Khouja (2005) extended the classical economic production lot size (EPL) model to cases where production rate is a decision variable. Unit production cost became a function of production rate. He solved the proposed model for special unit production cost functions and illustrated the results with a numerical example (Khouja 2005). Hou (2007) considered an EPQ model with imperfect production processes, in which the setup cost and process quality are functions of capital expenditure. Hariga (1996) developed optimal inventory lot-sizing models for deteriorating items with general continuous time-varying demand over a finite planning horizon and under three replenishment policies. Darwish (2008) extended the classical EPQ model by considering a relationship between setup cost and the production run length. The results show that the relationship between the cost function and the production time can have a signification effect on the economical production quantity and the average amount of the total cost in EPQ classic model. Vishkaei et al. (2014) extended Hsu and Hsu (2012) aiming to determine the optimal order quantity of product batches that contain defective items with percentage nonconforming following a known probability density function. The orders are subject to 100 % screening process at a rate higher than the demand rate. Shortage is backordered, and defective items in each ordering cycle are stored in a warehouse to be returned to the supplier when a new order is received. Seyedhoseini et al. (2015) have considered an inventory system with two substitute products with ignorable lead time and stochastic demand and by means of queuing theory a mathematical model has been proposed.

The holding cost is explicitly assumed to be varying over time in only few inventory models. Giri et al. (1996) considered a generalized EOQ model for deteriorating items here in which the demand rate, deterioration rate, holding cost and ordering cost are all assumed to be continuous functions of time. Ferguson et al. (2007) considered a variation of the economic order quantity (EOQ) model where cumulative holding cost is a nonlinear function of time. They showed how it is an approximation of the optimal order quantity for perishable goods, such as milk, and produce, sold in small to medium size grocery stores where there are delivery surcharges due to infrequent ordering, and managers frequently utilize markdowns to stabilize demand as the product’s expiration date nears (Ferguson et al. 2007). Also, they showed how the holding cost curve parameters can be estimated via a regression approach from the product’s usual holding cost (storage plus capital costs), lifetime, and markdown policy (Ferguson et al. 2007). Alfares (2007) considered the inventory policy for an item with a stock level-dependent demand rate and a storage time-dependent holding cost. The holding cost per unit of the item per unit time is assumed to be an increasing function of the time spent in storage. Two time-dependent holding cost step functions are considered: retroactive holding cost increase, and incremental holding cost increase. Procedures are developed for determining the optimal order quantity and the optimal cycle time for both cost structures. Ray and Chaudhuri (1997) took the time value of money into account in analyzing an inventory system with stock-dependent demand rate and shortages. Two types of inflation rates are considered: internal (company) inflation, and external (general economy) inflation. Shao et al. (2000) determined the optimum quality target for a manufacturing process where several grades of customer specifications may be sold. Since rejected goods could be stored and sold later to another customer, variable holding costs are considered in the model. Beltran and krass (2002) analyzed a version of the dynamic lot size (DLS) model where demands can be positive and negative and disposals of excess inventory are allowed. Assuming deterministic time-varying demands and concave holding costs, an efficient dynamic programming algorithm is developed for this finite time horizon problem. Goh (1992) apparently provides the only existing inventory model in which the demand is stock dependent and the holding cost is time dependent. Actually, he considered two types of holding cost variation: (1) a nonlinear function of storage time and (2) a nonlinear function of storage level (Goh 1992).

The first attempts to determine the optimal ordering policies for deteriorating items were made in (Ghare and Schrader 1963). They presented an EOQ model for an exponentially decaying inventory. Philip (1974) developed an inventory model with a three parameter Weibull distribution rate without considering shortages. Deb and Chaudhuri (1986) derived inventory model with time-dependent deterioration rate. Mishra et al. (2013) developed a deterministic inventory model with time-dependent demand and time-varying holding cost where deterioration is time proportional. A detailed review of deteriorating inventory literatures is given in Goyal and Giri (2001). Wu et al. (2006) developed an inventory model for non-instantaneous deteriorating items with partial backlogging where demand is assumed to be stock dependent. In Geetha and Uthayakumar (2010) EOQ-based model for non-instantaneous deteriorating items with permissible delay in payments is proposed. This model aids in minimizing the total inventory cost by finding an optimal replenishment policy. Valliathal and Uthayakumar (2011) discussed the optimal pricing and replenishment policies of an EOQ model for non-instantaneous deteriorating items with partial backlogging over an infinite time horizon. The model was studied under the replenishment policy starting with no shortages.

Chang et al. (2014) considered an inventory system with non-instantaneously deteriorating items under order size-dependent delay in payments. Soni and Patel (2013) developed an inventory model for non-instantaneous deteriorating items with imprecise deterioration free time and credibility constraint. That model assumes price-sensitive demand when the product has no deterioration and price and time-dependent demand when the product has deterioration. Shah et al. (2013) considered an inventory system with non-instantaneous deteriorating item in which demand rate was a function of advertisement of an item and selling price. Maihami and Karimi (2014) developed one model for determining the optimal pricing and replenishment policy for non-instantaneous deterioration items with promotional efforts. The demand was stochastic and dependent on price. Maihami and Kamalabadi (2012) developed a joint pricing and inventory control for non-instantaneous deteriorating items. They adopted a price- and time-dependent demand function. Tat et al. (2013) developed an EOQ model for non-instantaneous deteriorating items with and without shortages to investigate the performance of the vendor-managed inventory (VMI) system.

To the author’s knowledge, none of the above models considered the holding cost as a function of the ordering run length, but holding cost may not always be constant. This is particularly true in the storage of deteriorating and perishable items such as food products. Therefore, based on above discussion, this paper considers an inventory system with non-instantaneous deteriorating item in which holding cost is a function of the ordering run length.

Assumptions and notation

Consider a process with the following assumptions: the rate of demand is fixed, there is no discount, the delivery of the product is wholesale, all parameters are fixed and deterministic. The following notation will be used in developing the proposed models:

$D$ :

Demand rate

$Q$ :

Order quantity (decision variable)

$P$ :

Production rate $(P > D)$

$T$ :

Inventory cycle length

$T_{P}$ :

Production run length

K :

The cost of ordering or setup in the period of main orders

$h_{0}$ :

Holding cost per unit per time unit

$B$ :

The quantity of backorder (decision variable)

$\pi$ :

Shortage cost per item per unit time

TC:

Annual total cost

TOC:

Annual setup cost

THC:

Annual holding cost

TSC:

Annual backorder cost

Models development

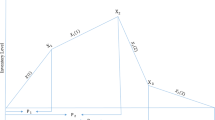
In this section, EPQ models for non-instantaneous deteriorating items are developed by considering a relationship between the holding cost and the ordering cycle length in two cases. First, the proposed model is considered when backorders are not permitted and for the second case this condition is waived. The behavior of inventory level for non-instantaneous deteriorating items is shown in Fig. 1. It is assumed that the holding cost will be fixed till a definite time $(T^{'} )$ and then will be increased as a function of ordering cycle length. This is because there is no deterioration in the inventory item until that point of time; after the time point $T^{'}$, deterioration commences and more effort and sophisticated storage facilities and services are needed, consequently increasing the holding cost. To determine this relation, the following equation is modified from that of Darwish (2008) and Jaber and Bonney (2003).

Fig. 1

Behavior of inventory level

$$ h(T) = \left\{ {\begin{array}{*{20}c} {h_{0} T^{\varepsilon } } & {T > T^{'} } \\ {h_{\hbox{min} } } & {T \le T^{'} } \\ \end{array} } \right.\quad 0\le \varepsilon \le 1 $$

(1)

where $T^{'}$ is a time moment before which the holding cost is constant. Therefore, before $T^{'}$ the holding activity requires a cost equal to $h_{min }$. However, after the time duration $T^{'}$, the holding process requires extra effort and holding cost escalates with the inventory cycle length. The factor $\varepsilon$ is the shape factor of holding cost. The parameter $h_{0}$ is a positive constant that can be interpreted as holding cost associated with the classical EPQ model ($\varepsilon = 0$). $h_{0}$ is actually equal to $h_{ \hbox{min} }$. It is clear that in Eq. (1) if $\varepsilon = 0$, the presented model will reflect the results of classical models. The parameter $h_{{{ \hbox{min} } }}$ serves as a lower limit on the holding cost. The behavior of $h(T)$ for different values of $\varepsilon \ge 0$ is shown in Fig. 2. In this study, it is required that $\varepsilon \ge 0$; however, one cannot ignore the possibility of having $\varepsilon < 0$, when the holding cost decreases gradually. This situation may be valid when the learning effect overcomes the effects of deterioration.

Fig. 2

Holding cost against ordering cycle length for different values of ε

Model 1: proposed EPQ model without backorders

In this model, it is assumed that the total amount of the ordered products is delivered gradually with rate of P and backorders are not allowed, as is shown in Fig. 3. Here, it is assumed that extra effort in period $T > T^{'}$ overcomes deterioration and causes to decrease of inventory level due to demand only. To find the optimal solution, we divide ${\text{TC}}$ into two components, one for $T \le T^{'}$ and the other for $T > T^{'}$. In the earlier case, the model becomes the classical EPQ model with a holding cost of $h_{\text{min }}$. But, for $T > T^{'}$ the optimal solution can be set out as follows.

Fig. 3

EPQ model without backorders

The annual total cost is summation of setup and holding costs and is calculated based on the following procedures.

$$ {\text{TC}} = {\text{TOC}} + {\text{THC}} $$

(2)

$$ {\text{TC}} = \frac{DK}{Q} + \frac{hQ}{2}\left( {1 - \frac{D}{P}} \right) $$

(3)

Replacing Eq. (1) in Eq. (3) yields

$$ {\text{TC}} = \left\{ {\begin{array}{*{20}c} {\frac{DK}{Q} + \frac{{h_{0} T^{\varepsilon } Q}}{2}\left( {1 - \frac{D}{P}} \right)} & {T > T^{'} } \\ {\frac{DK}{Q} + \frac{{h_{\hbox{min} } Q}}{2}\left( {1 - \frac{D}{P}} \right)} & {T \le T^{'} } \\ \end{array} } \right. $$

(4)

The total cost function in terms of $T$ can be set out as

$$ {\text{TC}} = \left\{ {\begin{array}{*{20}c} {\frac{K}{T} + \frac{{h_{0} DT^{\varepsilon + 1} }}{2}\left( {1 - \frac{D}{P}} \right)} & {T > T^{'} } \\ {\frac{K}{T} + \frac{{h_{\hbox{min} } DT}}{2}\left( {1 - \frac{D}{P}} \right)} & {T \le T^{'} } \\ \end{array} } \right. $$

(5)

Theorem 1

If $\varepsilon \ge 0$ and $T > T^{'}$ then

• 1. $TC$ is strictly convex.

• 2. The optimal value of $T$ is given by

$$ T^{*} = \sqrt[{\varepsilon + 2}]{{\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}}} $$

(6)

• 3. The resulting optimal order quantity, $Q^{*}$, production run length, $T_{P}^{*}$, and annual total cost, ${\text{TC}}^{*}$, are as follows:

$$ Q^{*} = D\sqrt[{\varepsilon + 2}]{{\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}}} $$

(7)

$$ T_{P}^{*} = \frac{D}{P}\sqrt[{\varepsilon + 2}]{{\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}}} $$

(8)

$$ {\text{TC}}^{*} = K\sqrt[{\varepsilon + 2}]{{\frac{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}{2KP}}} + \frac{{h_{0} D}}{2}\left( {\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}} \right)^{{\frac{\varepsilon + 1}{\varepsilon + 2}}} \left( {1 - \frac{D}{P}} \right) $$

(9)

Proof

Taking the first derivative of total cost function TC given by Eq. (5) with respect to $T$ yields

$$ \frac{{d{\text{TC}}}}{dT} = \frac{ - K}{{T^{2} }} + \left( {\varepsilon + 1} \right)\frac{{h_{0} D}}{2}\left( {1 - \frac{D}{P}} \right)T^{\varepsilon } $$

(10)

To minimize ${\text{TC}}(T),$ we set $\frac{{d{\text{TC}}}}{dT} = 0$ and obtain the optimal value of $T$ as Eq. (6).

The second derivative of total cost function ${\text{TC}}(T)$ is:

$$ \frac{{d^{2} {\text{TC}}}}{{dT^{2} }} = \frac{2K}{{T^{3} }} + \varepsilon \left( {\varepsilon + 1} \right)T^{\varepsilon - 1} \frac{{h_{0} D}}{2}\left( {1 - \frac{D}{P}} \right) $$

(11)

Since $0 \le \varepsilon \le 1,$ the Eq. (11) is always positive and consequently the function ${\text{TC}}(T)$ is convex, therefore, $T^{*}$ is global minimum.

The part (3) will be resulted from replacing $T^{*}$ in appropriate formula, namely $Q^{*} = DT^{*}$, $T_{P}^{*} = \frac{{Q^{*} }}{P} = \frac{{DT^{*} }}{P}$ and Eq. (5).

Therefore, the optimal solution can be set out as follows:

$$ T^{*} = \left\{ {\begin{array}{ll} {\sqrt[{\varepsilon + 2}]{{\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}}}} & {T > T^{'} } \\ {\frac{2K}{{h_{\hbox{min} } D}}} & {T \le T^{'} } \\ \end{array} } \right. $$

(12)

$$ {\text{TC}}^{*} = \left\{ {\begin{array}{ll} {K\sqrt[{\varepsilon + 2}]{{\frac{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}{2KP}}} + \frac{{h_{0} D}}{2}\left( {\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}} \right)^{{\frac{\varepsilon + 1}{\varepsilon + 2}}} \left( {1 - \frac{D}{P}} \right)} & {T > T^{'} } \\ {\sqrt {2DKh_{\hbox{min} } } } & {T \le T^{'} } \\ \end{array} } \right. $$

(13)

However, Eq. (6) may give rise to a case where the run length is not feasible $(T \le T^{'} )$. In this case we compare ${\text{TC}}(T^{'} )$ with $\sqrt {2DKh_{\hbox{min} } }$, where the optimal solution corresponds to the least cost. The following algorithm is devised to find the optimal solution:

Step 1 Compute $T$ by Eq. (6).

Step 2 If $T > T^{'}$, then $T^{*} = T$ and set

${\text{TC}}^{*} = K\sqrt[{\varepsilon + 2}]{{\frac{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}{2KP}}} + \frac{{h_{0} D}}{2}\left( {\frac{2KP}{{\left( {\varepsilon + 1} \right)\left( {P - D} \right)h_{0} D}}} \right)^{{\frac{\varepsilon + 1}{\varepsilon + 2}}} \left( {1 - \frac{D}{P}} \right)$, go to step 6.

Step 3 If $T \le T^{'}$ determine

$$ {\text{TC}}_{1} = \frac{K}{{T^{\prime}}} + \frac{{h_{0} DT^{'\varepsilon + 1} }}{2}\left( {1 - \frac{D}{P}} \right) $$

$$ {\text{TC}}_{2} = \sqrt {2DKh_{\hbox{min} } } $$

Step 4 If ${\text{TC}}_{1} < {\text{TC}}_{2}$ then $T^{*} = T^{'}$ and ${\text{TC}}^{*} = {\text{TC}}_{1}$ and go to step 6.

Step 5 If ${\text{TC}}_{1} \ge {\text{TC}}_{2}$ then we use the classical EPQ models formulas, in that case we have $h_{\hbox{min} } = h_{0}$, so $T^{*} = \sqrt {\frac{2K}{{h_{\hbox{min} } D}}}$ and ${\text{TC}}^{*} = {\text{TC}}_{2}$ and go to step 6.

Step 6 Stop.

Numerical example 1

This section demonstrates the utility of the model and studies the effect of the shape parameter of holding cost on the optimal solution. To assess the difference from using the classical EPQ model, its performance is compared with that of the proposed model. Let ${\text{TC}}_{\text{EPQ}}^{*}$ denote the optimal total expected cost using the classical EPQ model ($\varepsilon = 0$). Now define the percent loss due to using the classical EPQ model instead of the proposed model as $\% {\text{loss}} = \frac{{{\text{TC}}^{*} - {\text{TC}}_{\text{EPQ}}^{*} }}{{{\text{TC}}_{\text{EPQ}}^{*} }} \times 100$. Then, we use following data for numerical example. The parameters of the numerical examples are borrowed from Darwish (2008). However, some of the parameters were altered to reflect $h_{0}$, $h_{\hbox{min} }$, $\varepsilon$. The following data are used:

The annual demand of a material is 20,000, its setup cost is 100, its holding cost is 10 annually and the rate of production is 25,000. Table 1 gives the optimal solutions for selected values of $\varepsilon$ ranging from 0 to 1 with an increment of 0.1. It is worth noting that the value of $\varepsilon$, which depends on the production process, defines the type of the production system under consideration. For values of $\varepsilon$ closer to zero, the proposed model gives results closer to the EPQ model with relatively lower lot size, shorter production run and shorter ordering cycle length. The results show that the production run length and ordering cycle length increase as $\varepsilon$ increases. Furthermore, total cost decreases as $\varepsilon$ increases. The results also indicate that the lot size is inflating as $\varepsilon$ increases, which leads to a lower expected total cost. Important observation is that the difference brought about using the classical EPQ model increases with $\varepsilon$. This is because for high values of $\varepsilon ,$ the holding cost in the classical EPQ deviates from the actual situation. Figure 4 shows total cost versus cycle length for $\varepsilon = 0.1$; here minimum value of total cost is 2490.4 for T = 0.0767.

Table 1 Optimal solution for different values of ε when backorders are not allowed

Fig. 4

Total cost vs. cycle length for $\varepsilon = 0.1$ (Sect. “Numerical example 1”)

Model 2: proposed EPQ model with backorders

In this model, we assume that the total amount of the ordered materials will be delivered gradually and backorders are allowed. Figure 5 shows this model.

Fig. 5

EPQ model with backorders

To find the optimal solution, we use the approach in Sect. 3.1 by considering two cases of $(T \le T^{'} )$ and $(T \ge T^{'} )$. The first case represents the classical EPQ model with backorders. However, the optimal solution for $(T \ge T^{'} )$ is established in the following theorem.

Theorem 2

If $0 \le \varepsilon \le 1$ and $T > T^{'}$ then

• 1. The optimal value of $T$ is gained by solving Eq. (14).

• 2. The optimal value of $B$ is given by Eq. (15).

$$ \begin{aligned} &- 2KP\left( {h_{0} PT^{\varepsilon } + \pi P} \right)^{2} + \left( {\varepsilon + 1} \right)h_{0} D\left( {P -D} \right)T^{\varepsilon + 2} \left( {h_{0} PT^{\varepsilon } + \pi P} \right)^{2}\\ &- 2\varepsilon h_{0}^{2} PD\left( {P - D} \right)T^{2\varepsilon +2} \left( {h_{0} PT^{\varepsilon } + \pi P} \right) \hfill \\ &+ \left( {\varepsilon - 1} \right)h_{0}^{3} P^{2} D\left( {P - D} \right)T^{3\varepsilon + 2} - \pi h_{0}^{2} P^{2} D\left( {P - D} \right)T^{2\varepsilon + 2} = 0 \hfill \\ \end{aligned} $$

(14)

$$ B^{*} = \frac{{h_{0} \left( {P - D} \right)T^{{*^{\varepsilon + 1} }} }}{{h_{0} PT^{{*^{\varepsilon } }} + \pi P}} $$

(15)

• 3. The resulting optimal order quantity, $Q^{*}$, production run length, $T_{p}^{*}$, annual total cost time, ${\text{TC}}^{*}$, are as follows:

$$ T_{P}^{*} = \frac{{Q^{*} }}{P},Q^{*} = DT^{*} $$

$$ {\text{TC}}^{*} = \frac{K}{{T^{*} }} + \frac{{h_{0} D}}{2P}\left( {P - D} \right)T^{{*^{\varepsilon + 1} }} - h_{0} B^{*} T^{{*^{\varepsilon } }} + \frac{{h_{0} PB^{{*^{2} }} T^{{*^{\varepsilon - 1} }} }}{{2D\left( {P - D} \right)}} + \frac{{\pi PB^{{*^{2} }} }}{{2D\left( {P - D} \right)T^{*} }} $$

(16)

Proof

See Appendix.

The proof of the convexity of TC is provided in Appendix. The overall convexity of total cost is not guaranteed; however, in special cases, convexity can be approved. These cases are considered in Appendix, too. Furthermore, the convexity of the cost function is shown graphically in the Numerical example 2. An algorithm similar to that of Sect. “Model 1: proposed EPQ model without backorders” is utilized to determine the optimal solution.

Numerical example 2

The data presented in Sect. “Numerical example 1” are used to investigate the effect of $\varepsilon$ on the optimal solution. It should be noted that, here, shortage cost per item per unit time is 15. When the shape parameter, $\varepsilon$, decreases, the holding cost in the proposed model is close to that in the classical EPQ model. As a result, the optimal values of $T^{*} ,B^{*}$, $Q^{*}$, $T_{P}^{*}$ and ${\text{TC}}^{*}$ are closer to the classical EPQ model when $\varepsilon$ is low; this observation is shown in Table 2. The results indicate that when $\varepsilon$ increases, the optimal backorder level $B^{*}$ decreases because the production system is set up more frequently for high values of $\varepsilon$. Moreover, for high values of $\varepsilon$, the optimal production quantity decreases.

Table 2 Optimal solution for different values of ε when backorders are allowed

Table 2 also shows that significant losses happen when the classical EPQ model is used instead of the proposed model; for example, a change of 31.28 % of the total cost is observed if the classical EPQ model is employed when $\varepsilon = 0.5$. The results also show that the optimal production run length, cycle time, lot size and expected total cost per unit time are very sensitive to $\varepsilon$. For example, Fig. 6 shows total cost versus cycle length and backorder for $\varepsilon = 0.5$; here minimum value of total cost is 1505.6 for T = 0.1136, B = 83.4.

Fig. 6

Total cost versus cycle length and backorder for $\varepsilon = 0.5$

Conclusions and suggestions

In this paper, the classical EPQ models have been developed for non-instantaneous deteriorating items by considering holding cost as an increasing continuous function of ordering cycle length. It was assumed that the holding cost would stay fixed till a definite time and then would increase as a function of ordering cycle length. Two models were developed. The first for the case when backorders were not allowed and other one permitted backorders. The optimization algorithm has been developed, and numerical examples have been solved. Economic ordering quantity, EPQ, the optimum cycle length and the optimum total cost all were determined. From the numerical results, we could clearly see variation due to use of the classical EPQ model. Based on the formulas developed, it can be concluded that both the optimal order quantity and the cycle time increase when the holding cost increases. As the shape parameter $\varepsilon$ increases, the total cost decreases while the optimal order quantity and the cycle time increase. Moreover, the optimal order quantity and the EPQ are equal when $\varepsilon = 0$. The model presented in this study provides a basis for several possible extensions. For future research, this model can be extended to accommodate variable ordering costs. The case of the increasing holding cost that was considered in this paper, applies to company-owned storage facilities, and particularly to perishable items that require extra care if stored for longer periods. Another extension possibility would be to consider holding cost as a kind of decreasing function of the ordering cycle length. Since a decreasing holding cost is applicable to rented storage facilities, lower rent rates are obtained for longer term leases.

Appendix

The annual total cost is sum of setup, holding and shortage costs and it is calculated based on the following procedures.

$$ {\text{TC}}(T,B) = {\text{TOC}} + {\text{THC}} + {\text{TSC}} $$

(17)

$$ {\text{TC}}(T,B) = \frac{DK}{Q} + \frac{{h\left( {Q\left( {1 - \frac{D}{P}} \right) - B} \right)^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} + \frac{{\pi B^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} $$

(18)

Replacing $h$ from Eq. (1) in Eq. (18) yields:

$$ {\text{TC}}(T,B) = \left\{ \begin{aligned} \frac{DK}{Q} + \frac{{h_{0} T^{\varepsilon } \left( {Q\left( {1 - \frac{D}{P}} \right) - B} \right)^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} + \frac{{\pi B^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} \, T > T^{'} \hfill \\ \frac{DK}{Q} + \frac{{h_{\hbox{min} } \left( {Q\left( {1 - \frac{D}{P}} \right) - B} \right)^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} + \frac{{\pi B^{2} }}{{2Q\left( {1 - \frac{D}{P}} \right)}} \, T \le T^{'} \hfill \\ \end{aligned} \right. $$

(19)

For $T > T^{'}$ we have

$$ {\text{TC}}(T,B) = \frac{K}{T} + \frac{{h_{0} T^{\varepsilon } \left( {DT\left( {1 - \frac{D}{P}} \right) - B} \right)^{2} }}{{2DT\left( {1 - \frac{D}{P}} \right)}} + \frac{{\pi B^{2} }}{{2DT\left( {1 - \frac{D}{P}} \right)}} $$

(20)

$$ {\text{TC}}(T,B) = \frac{K}{T} + \frac{{h_{0} PT^{\varepsilon - 1} \left( {\frac{D}{P}\left( {P - D} \right)T - B} \right)^{2} }}{{2D\left( {P - D} \right)}} + \frac{{\pi PB^{2} }}{{2DT\left( {P - D} \right)}} $$

(21)

$$ {\text{TC}}(T,B) = \frac{K}{T} + \frac{{h_{0} D}}{2P}\left( {P - D} \right)T^{\varepsilon + 1} - h_{0} BT^{\varepsilon } + \frac{{h_{0} PB^{2} T^{\varepsilon - 1} }}{{2D\left( {P - D} \right)}} + \frac{{\pi PB^{2} }}{{2DT\left( {P - D} \right)}} $$

(22)

The gradient of ${\text{TC}}(T,B)$ function will be as follows

$$ \nabla {\text{TC}}(T,B) = \left( {\frac{{\partial {\text{TC}}\left( {T,B} \right)}}{\partial T},\frac{{\partial {\text{TC}}\left( {T,B} \right)}}{\partial B}} \right) $$

(23)

$$ \frac{{\partial {\text{TC}}(T,B)}}{\partial T} = - \frac{K}{{T^{2} }} + \frac{{\left( {\varepsilon + 1} \right)h_{0} D(P - D)T^{\varepsilon } }}{2P} - \varepsilon h_{0} BT^{\varepsilon - 1} + \frac{{\left( {\varepsilon - 1} \right)h_{0} PB^{2} T^{\varepsilon - 2} }}{2D(P - D)} - \frac{{\pi PB^{2} }}{{2D\left( {P - D} \right)T^{2} }} $$

(24)

$$ \frac{{\partial {\text{TC}}(T,B)}}{\partial B} = - h_{0} T^{\varepsilon } + \frac{{h_{0} PBT^{\varepsilon - 1} }}{D(P - D)} - \frac{\pi PB}{{DT\left( {P - D} \right)}} $$

(25)

The Hessian matrix of ${\text{TC}}(T,B)$ function is given by

$$ H = \left[ \begin{aligned} \frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial T^{2} }} \,\quad \frac{{\partial^{2} {\text{TC}}(T,B)}}{\partial B\partial T} \hfill \\ \frac{{\partial^{2} {\text{TC}}(T,B)}}{\partial T\partial B} \,\quad \frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial B^{2} }} \, \hfill \\ \end{aligned} \right] $$

where

$$ \frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial T^{2} }} = \frac{2K}{{T^{3} }} + \frac{{\varepsilon \left( {\varepsilon + 1} \right)h_{0} D(P - D)T^{\varepsilon - 1} }}{2P} - \varepsilon (\varepsilon - 1)h_{0} BT^{\varepsilon - 2} + \frac{{\left( {\varepsilon - 1} \right)\left( {\varepsilon - 2} \right)h_{0} PB^{2} T^{\varepsilon - 3} }}{2D(P - D)} + \frac{{\pi PB^{2} }}{{D\left( {P - D} \right)T^{\varepsilon } }} $$

(26)

$$ \frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial B^{2} }} = \frac{{h_{0} PT^{\varepsilon - 1} }}{D(P - D)} + \frac{\pi P}{DT(P - D)} $$

(27)

$$ \frac{{\partial^{2} {\text{TC}}(T,B)}}{\partial T\partial B} = - \varepsilon h_{0} T^{\varepsilon - 1} + \frac{{\left( {\varepsilon - 1} \right)h_{0} PBT^{\varepsilon - 2} }}{D(P - D)} - \frac{\pi PB}{{D\left( {P - D} \right)T^{2} }} $$

(28)

$$ \frac{{\partial^{2} {\text{TC}}(T,B)}}{\partial B\partial T} = - \varepsilon h_{0} T^{\varepsilon - 1} + \frac{{\left( {\varepsilon - 1} \right)h_{0} PBT^{\varepsilon - 2} }}{D(P - D)} - \frac{\pi PB}{{D\left( {P - D} \right)T^{2} }} $$

(29)

Since $0 \le \varepsilon \le 1$, then $\frac{{\delta^{2} {\text{TC}}(T, B)}}{{\delta T^{2} }}$ is always positive and the determinant of the $H$ provided from Eq. (30).

$$ \begin{aligned} \left| H \right| &= \left({\frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial T^{2} }}}\right)\left( {\frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial B^{2} }}} \right) - \left( {\frac{{\partial^{2}{\text{TC}}(T,B)}}{\partial T\partial B}} \right)^{2} \hfill \\ &= \frac{{2Kh_{0} PT^{\varepsilon - 4} }}{D(P - D)} + \frac{{\varepsilon (\varepsilon + 1)h_{0}^{2} T^{2\varepsilon - 2}}}{2} - \frac{{\varepsilon (\varepsilon - 1)h_{0}^{2} PBT^{2\varepsilon - 3} }}{D(P - D)} + \frac{{(\varepsilon -1)(\varepsilon - 2)h_{0}^{2} P^{2} B^{2} T^{2\varepsilon - 4}}}{{2D^{2} (P - D)^{2} }} + \frac{{h_{0} \pi P^{2} B^{2}T^{\varepsilon - 4} }}{{D^{2} (P - D)^{2} }} \hfill \\ &\quad+\frac{{2K\pi PT^{ - 4} }}{D(P - D)} + \frac{{\varepsilon(\varepsilon + 1)h_{0} \pi T^{\varepsilon - 2} }}{2} -\frac{{\varepsilon (\varepsilon - 1)h_{0} \pi PBT^{\varepsilon - 3}}}{D(P - D)} + \frac{{(\varepsilon - 1)(\varepsilon - 2)h_{0} \pi P^{2} B^{2} T^{\varepsilon - 4} }}{{2D^{2} (P - D)^{2} }} +\frac{{\pi^{2} P^{2} B^{2} T^{ - 4} }}{{D^{2} (P - D)^{2} }} \hfill\\ &\quad- \varepsilon^{2} h_{0}^{2} T^{2\varepsilon - 2} +\frac{{\varepsilon (\varepsilon - 1)h_{0}^{2} PBT^{2\varepsilon - 3}}}{D(P - D)} - \frac{{\varepsilon h_{0} \pi PBT^{\varepsilon - 3}}}{D(P - D)} + \frac{{\varepsilon (\varepsilon - 1)h_{0}^{2}PBT^{2\varepsilon - 3} }}{D(P - D)} - \frac{{(\varepsilon -1)h_{0}^{2} P^{2} B^{2} T^{2\varepsilon - 4} }}{{D^{2} (P - D)^{2}}} \hfill \\ &\quad+ \frac{{(\varepsilon - 1)h_{0} \pi P^{2} B^{2}T^{\varepsilon - 4} }}{{D^{2} (P - D)^{2} }} - \frac{{\varepsilon h_{0} \pi PBT^{\varepsilon - 3} }}{D(P - D)} + \frac{{(\varepsilon -1)h_{0} \pi P^{2} B^{2} T^{\varepsilon - 4} }}{{D^{2} (P - D)^{2} }}- \frac{{\pi^{2} P^{2} B^{2} T^{ - 4} }}{{D^{2} (P - D)^{2} }}\hfill \\ &= \frac{{2Kh_{0} PT^{\varepsilon - 4} }}{D(P - D)} +\frac{{\varepsilon (\varepsilon + 1)h_{0}^{2} T^{2\varepsilon - 2}}}{2} + \frac{{(\varepsilon - 1)(\varepsilon - 2)h_{0}^{2} P^{2}B^{2} T^{2\varepsilon - 4} }}{{2D^{2} (P - D)^{2} }} + \frac{{h_{0}\pi P^{2} B^{2} T^{\varepsilon - 4} }}{{D^{2} (P - D)^{2} }} +\frac{{2K\pi PT^{ - 4} }}{D(P - D)} \hfill \\ &\quad+ \frac{{\varepsilon (\varepsilon + 1)h_{0} \pi T^{\varepsilon - 2}}}{2} - \frac{{\varepsilon (\varepsilon - 1)h_{0} \pi PBT^{\varepsilon - 3} }}{D(P - D)} + \frac{{(\varepsilon -1)(\varepsilon - 2)h_{0} \pi P^{2} B^{2} T^{\varepsilon - 4}}}{{2D^{2} (P - D)^{2} }} - \varepsilon^{2} h_{0}^{2}T^{2\varepsilon - 2} - \frac{{2\varepsilon h_{0} \pi PBT^{\varepsilon - 3} }}{D(P - D)} \hfill \\ &\quad+\frac{{\varepsilon (\varepsilon - 1)h_{0}^{2} PBT^{2\varepsilon - 3}}}{D(P - D)} - \frac{{(\varepsilon - 1)h_{0}^{2} P^{2} B^{2}T^{2\varepsilon - 4} }}{{D^{2} (P - D)^{2} }} + \frac{{2(\varepsilon- 1)h_{0} \pi P^{2}B^{2} T^{\varepsilon - 4} }}{{D^{2} (P - D)^{2} }} \hfill \\ \end{aligned}$$

(30)

Verification of the sign of Eq. (30) seems to be impossible, as while $\varepsilon = 1$ we have

$$ \begin{aligned} \left| H \right| &= \frac{{2Kh_{0} PT^{ - 3}}}{D(P - D)} + h_{0}^{2} + \frac{{h_{0} \pi P^{2} B^{2} T^{ - 3}}}{{D^{2} (P - D)^{2} }} + \frac{{2K\pi PT^{ - 4} }}{D(P - D)} +h_{0} \pi T^{ - 1} - h_{0}^{2} - \frac{{2h_{0} \pi PBT^{ - 2} }}{D(P- D)} \hfill \\ &= \frac{{2K\pi PT^{ - 4} }}{D(P - D)} +\frac{{h_{0} \pi P^{2} B^{2} T^{ - 3} }}{{D^{2} (P - D)^{2} }} +\frac{{2Kh_{0} PT^{ - 3} }}{D(P - D)} - \frac{{2h_{0} \pi PBT^{ - 2}}}{D(P - D)} + h_{0} \pi T^{ - 1} \hfill \\ &= \frac{{2K\pi PD(P -D) + h_{0} \pi P^{2} B^{2} T + 2Kh_{0} PTD(P - D) - 2h_{0} \pi PBT^{2} D(P - D) + h_{0} \pi T^{3} D^{2} (P - D)^{2} }}{{D^{2} (P -D)^{2} T^{4} }} \hfill \\ \end{aligned} $$

(31)

While $\varepsilon = 1$, if one of the following conditions [Eqs. (32)–(36)] is realized, the determinant of $H$ would not be negative and ${\text{TC}}(T,B)$ will be convex. It should be mentioned that this condition is not the most essential condition but is an adequate one.

$$ 2K\pi PD(P - D) + h_{0} \pi P^{2} B^{2} T + 2Kh_{0} PTD(P - D) - 2h_{0} \pi PBT^{2} D(P - D) + h_{0} \pi T^{3} D^{2} (P - D)^{2} > 0 $$

(32)

$$ 2K\pi PD(P - D) > 2h_{0} \pi PBT^{2} D(P - D) \Rightarrow k > BT^{2} $$

(33)

$$ h_{0} \pi P^{2} B^{2} T > 2h_{0} \pi PBT^{2} D(P - D) \Rightarrow PB > 2D(P - D)T $$

(34)

$$ 2Kh_{0} PTD(P - D) > 2h_{0} \pi PBT^{2} D(P - D) \Rightarrow K > \pi BT $$

(35)

$$ h_{0} \pi T^{3} D^{2} (P - D)^{2} > 2h_{0} \pi PBT^{2} D(P - D) \Rightarrow D(P - D)T > 2P $$

(36)

To find the minimum points of TC, we survey its condition as below.

The function TC is always positive and continuous for $T > 0$ and $B > 0$. Also, there is a section for which function TC is convex (when $T \to 0^{ + }$, $TC \to + \infty$).

When $T$ is positive the gradient vector is always available.

$\left( {\frac{{\partial^{2} {\text{TC}}(T,B)}}{{\partial T^{2} }}} \right)$ is always positive, therefore, the TC is not concave and so the extremum points would be in types of minimum points.

Consider the following:

The function TC does not have a local maximum point or a total maximum point. When $T \to 0^{ + }$, then ${\text{TC}} \to + \infty$; when $B \to 0^{ + }$, then ${\text{TC}} \to + \infty$; when $T \to + \infty$, then ${\text{TC}} \to + \infty$. Therefore, these cases provide just the following two conditions for function ${\text{TC}}(T,B).$

• 1. Function ${\text{TC}}(T,B)$ has just a local minimum point that will be considered as an optimal point which is obtained from solving Eq. (37). In this case, the Eq. (37) has only one real root.

• 2. Function TC(T, B) has some local minimum points and some saddle points that the maximum number of these points is $3\varepsilon + 2$. One of these points will be the optimal minimum point and the other points will be the local minimum point or saddle points. In this case, the Eq. (37) will have more than one real root. For these points, if the determinant of Hessian matrix is positive, then the point will be minimum, and if the determinant of Hessian matrix is negative, then the point will be saddle. Based on the aforementioned conditions, the ${\text{TC}}(T,B)$ function will certainly have an optimal minimum point. The optimal solution is one of the minimum points which has the lowest value of ${\text{TC}}$.

To find the optimal solution we have

$$ \nabla {\text{TC}}(T,B) = \left( {\frac{{\partial {\text{TC}}\left( {T,B} \right)}}{\partial T},\frac{{\partial {\text{TC}}\left( {T,B} \right)}}{\partial B}} \right) = 0 $$

(37)

$$ \frac{{\partial {\text{TC}}\left( {T,B} \right)}}{\partial T} = 0 \Rightarrow - \frac{K}{{T^{2} }} + \frac{{\left( {\varepsilon + 1} \right)h_{0} D(P - D)T^{\varepsilon } }}{2P} - \varepsilon h_{0} BT^{\varepsilon - 1} + \frac{{\left( {\varepsilon - 1} \right)h_{0} PB^{2} T^{\varepsilon - 2} }}{2D(P - D)} - \frac{{\pi PB^{2} }}{{2D\left( {P - D} \right)T^{2} }} = 0 $$

(38)

$$ \frac{{\partial {\text{TC}}(T,B)}}{\partial B} = 0 \Rightarrow - h_{0} T^{\varepsilon } + \frac{{h_{0} PBT^{\varepsilon - 1} }}{D(P - D)} - \frac{\pi PB}{{DT\left( {P - D} \right)}} = 0 $$

(39)

From Eq. (39) we get Eq. (15) and then the Eq. (40) is provided by replacing of $B$ from Eq. (15) in Eq. (38); finally we obtain optimal solution for $T$ by solving the Eq. (40) respect to T.

$$ \begin{aligned} &- 2KP\left( {h_{0} PT^{\varepsilon } + \pi P} \right)^{2} + \left( {\varepsilon + 1} \right)h_{0} D\left( {P - D}\right)T^{\varepsilon + 2} \times \left( {h_{0} PT^{\varepsilon } + \pi P}\right)^{2} - 2\varepsilon h_{0}^{2} PD\left( {P - D}\right)T^{2\varepsilon + 2} \left( {h_{0} PT^{\varepsilon } + \pi P}\right) \hfill \\ &\quad+ \left( {\varepsilon - 1} \right)h_{0}^{3}P^{2} D\left( {P - D} \right)T^{3\varepsilon + 2} - \pi h_{0}^{2}P^{2}D\left( {P - D} \right)T^{2\varepsilon + 2} = 0 \hfill \\ \end{aligned} $$

(40)