Optimal lot sizing in screening processes with returnable defective items

Abstract

This paper is an extension of Hsu and Hsu (Int J Ind Eng Comput 3(5):939–948, 2012) aiming to determine the optimal order quantity of product batches that contain defective items with percentage nonconforming following a known probability density function. The orders are subject to 100 % screening process at a rate higher than the demand rate. Shortage is backordered, and defective items in each ordering cycle are stored in a warehouse to be returned to the supplier when a new order is received. Although the retailer does not sell defective items at a lower price and only trades perfect items (to avoid loss), a higher holding cost incurs to store defective items. Using the renewal-reward theorem, the optimal order and shortage quantities are determined. Some numerical examples are solved at the end to clarify the applicability of the proposed model and to compare the new policy to an existing one. The results show that the new policy provides better expected profit per time.

Background

The economic order quantity (EOQ) is one of the most applicable models in inventory control environments that have been under significant studies for the past few decades. Researchers have extended this model considering various assumptions. One of the extension types of this model deals with imperfect quality products. Although most of suppliers do not implement 100 % screenings on their products, a complete screening process is indispensable for a retailer who desires to improve his market share.

Rosenblat and Lee (1986) were the first who focused on defective items. They considered the possibility of reworking defective items at a cost and proved this would cause smaller lot sizes to be ordered. Porteus (1986) studied a model in which there is a relationship between quality and lot size and assumed that the process would go out of control with a certain probability. Lee and Rosenblatt (1987) proposed an EOQ model considering random proportion of units as defective items. Salameh and Jaber (2000) developed an EOQ model with defective items in which the products are sold in a single batch at the end of 100 % screening process. They proved the more the average percentage of defective items is, the more economic lot size should be ordered. Hayek and Salameh (2001) studied an EPQ model by considering the imperfect quality products and rework items. They assumed all of the shortages are backordered and the percentage of defective products is a random variable. Goyal and Cárdenas-Barrón (2002) proposed an EPQ model under a simple approach to determine economic production quantity for production systems that produce imperfect quality items. Chan et al. (2003) categorized products into good quality, good quality after reworking, imperfect quality, or scrap. Their model’s other assumptions were similar to Salameh and Jaber’s (2000) model. Moreover, Chang (2004) proposed the fuzzy form of Salameh and Jaber’s (2000) model.

Huang (2004) extended the EPQ model in which imperfect products are allowed. Chiu et al. (2004) considered the effects of random defective rate and imperfect rework process on EPQ model. Chang (2004) investigated the effects of imperfect products on the total inventory cost associated with an EPQ model. Goyal and Cardenas-Barron (Goyal and Cárdenas-Barrón 2005) extended the EPQ model by considering imperfect production system that produces defective products. They assumed all of the defective items are reworked. Chiu et al. (2007) investigated an EPQ model that considers scrap, rework, and stochastic machine breakdowns to determine the optimal run time and production quantity. Wen-Kai and Hong-Fwu (2009) extended Salameh and Jaber’s (2000) model considering a one-time-only discount. They calculated the optimal order size for a special period in which discount is offered. Wee et al. (2007) added a shortage backordering assumption to Salameh and Jaber’s (2000) model. In their model, shortage is satisfied at the beginning of each period before the screening process. Therefore, defective items might have been shipped to customers.

Taleizadeh et al. (2010a) introduced an EPQ model with scrapped items and limited production capacity. They (Taleizadeh et al. 2010b) also introduced a multi-product single-machine production system with stochastic-scrapped production rate, partial backordering, and service level constraint. Furthermore, Taleizadeh et al. (2010c) studied a production quantity model with random defective items, service level constraints, and repair failure in multi-product single-machine situation.

Jaber et al. (2008) introduced an EPQ model for items with imperfect quality subject to learning effects. They assumed that imperfect quality items are withdrawn from inventory and sold at a discounted price. In another research, Jaber et al. (2013) modeled imperfect quality items under the push-and-pull effect of purchase and repair option in which the defectives were repaired at some cost or replaced by good items at some higher cost. They introduced optimal policies for each case. Khan et al. (2011) considered order quantity and lead time as decision variables in a production system with defective items. They defined the strategy of credit period for their model and used an algorithm to minimize the total cost of the system. Hauck and Vörös (2014) considered the percentage of defective items as a random variable and defined the speed of the quality checking as a variable. They developed two models: in one of them, no change would happen in the system state; and in the other, the state of the system might change after each order cycle. Mukhopadhyay and Goswami (2014) studied the effect of one-way substitutions of imperfect quality items to cope up with lost sales and shortages.

Yoo et al. (2009) proposed a profit-maximizing EPQ model that incorporates both imperfect production quality and two-way imperfect inspection. Hsu and Hsu (2012) corrected this model and showed that a significant difference would occur between the corrected model and the Wee et al.’s (2007) model. Besides, Chang and Ho (2010) revisited Wee et al.’s (2007) model and obtained a new expected net profit per unit time via the renewal-reward theorem. Moreover, Tai (2013) extended Hsu and Hsu’s (2012) model considering two warehouses and multi-screening processes. Other related researches are Cárdenas-Barrón (2000, 2007, 2009), Chandrasekaran et al. (2007), Liu et al. (2008), Mohan et al. (2008), and Parveen and Rao (2009).

This paper proposes another extension to Hsu and Hsu’s (2012) model by changing one of the assumptions. Instead of selling defective items at the end of a period at a lower price, a contractual money back agreement between the retailer and the supplier exists based on which the defective products are returned to the supplier via the vehicle that brings a new order in that period.

The remainder of this paper is organized as follows. A brief introduction is given for Hsu and Hsu’s (2012) model in the next section. The new formulation along with its optimal solution is proposed in “The new model”. The section titled “Numerical examples” contains illustrations to demonstrate the applicability of the proposed methodology and to compare its results with the ones obtained using Hsu and Hsu’s (2012) model. We conclude the paper in “Conclusion”.

Hsu and Hsu’s model

The parameters, the decision variables, and the assumptions involved in Hsu and Hsu’s (2012) model are described as follows.

Parameters

The parameters are:

D :

Demand rate

x :

Screening rate, x > D

c :

Purchasing cost per unit

K :

Ordering cost per order

p :

Random percentage defective

f (p):

Density function of p

s :

Selling price per unit

ν :

Salvage value per defective item, ν < c

d :

Screening cost per unit

b :

Backordering cost per unit per unit of time

h :

Holding cost per unit per unit of time

T :

Cycle time

t ₁ :

Part of the cycle time in which there is an inventory

t ₂ :

Part of the cycle time in which there is no item for shipping

t ₃ :

Part of the cycle time for screening

Decision variables

The decision variables are:

y :

Order size

B :

Maximum backordering quantity

Assumptions

The assumptions involved in the Hsu and Hsu’s (Hsu and Hsu 2012) model are:

• 1. The demand rate and the lead time are known and constant.

• 2. The replenishment is instantaneous.

• 3. Shortage is completely backordered.

• 4. To avoid shortage within screening time t, p ≤ 1−D/x.

• 5. The defective items are sold after finishing the screening process.

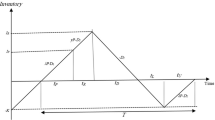
A graphical representation of the inventory problem at hand is shown in Fig. 1. The inventory begins with the order quantity y. Then, at the end of the screening process, t ₃ , B units are sold at a rate of x(1−p)−D. In this case, the optimal values of y and B can be obtained based on Eqs. 1 and 2.

Fig. 1

Inventory behavior over time in Hsu and Hsu’s (2012) model

$$y^{\ast }=\sqrt{\frac{2\text{KD}}{h\left\{E\left[{\left(1-p\right)}^2\right]-R^2{A}_1+2E\left[p\right]\frac{D}{x}\right\}-b{R}^2\left(1+A_3\frac{D}{x}\right)}}$$

(1)

$$B^{\ast }=y^{\ast }\times R$$

(2)

where

$$R=\frac{h\left(1-E\left[p\right]-\frac{A_{1}D}{x}-A_2\right)}{2\left(h{A}_1+b+\frac{b{A}_{3}D}{x}\right)}$$

(3)

and $A_1=E\left[\frac{\left(1-p\right)}{\left(1-p-\frac{D}{x}\right)}\right],A_2=E\left[\frac{{\left(1-p\right)}^2}{\left(1-p-\frac{D}{x}\right)}\right],A_3=E\left[\frac{1}{\left(1-p-\frac{D}{x}\right)}\right].$

The new model

In Hsu and Hsu’s (2012) model, defective items are sold at a price $\mathcal{V}$ each after finishing the screening process. However, in some industries such as apparel, crystal, electronic, and IT, it is not reasonable to sell the imperfect items at lower price since the difference between salvage and actual price is significant and suppliers use different policies to compensate the faults in their products. One of these policies is taking back the imperfect items. Therefore, in this paper, defective items received in a period are returned to the supplier at the beginning of the next period. In this case, the inventory behavior is changed to the one shown in Fig. 2. In this figure, at time t₁, all the perfect items are sold, and py defective items are remained unsold; kept in the warehouse until the beginning of the next delivery. Moreover, the payment occurs at the end of the screening process, t₃, and the retailer only pays the purchasing cost of perfect items that is (1−p)yc. Therefore, the holding cost of a period increases and that there is no revenue from selling defective items at a lower price. Instead, he returns them to the supplier at the end of the period when the supplier’s vehicle delivers the new order. As a result, the rate of satisfying backorders in each cycle is x(1−p)−D. After time t₃, the inventory reduces to $B+t_{3}D=x\left(1-p\right)t_3=\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}$ and so $t_3=\frac{B}{x\left(1-p\right)-D}$. Moreover, based on Fig. 2, $t_1=\frac{y\left(1-p\right)-B}{D},t_2=\frac{B}{D}$ and $T=\frac{\left(1-p\right)y}{D}$.

Fig. 2

Inventory behavior when defective items are returned

The ordering cost per cycle is K and the purchasing cost per cycle, TS, is

Note that the payment occurs only for (1−p)y items after the screening process, and the retailer does not pay for the py defective items.

The cost of the screening process per cycle, TD, is obtained by

$$TD=\text{d}y$$

(4)

The backordering cost per cycle, TB, is determined by

$$\begin{array}{c}TB=\frac{1}{2}bB\left(t_2+t_3\right)=\frac{1}{2}NbB\left(\frac{B}{D}+\frac{B}{x\left(1-p\right)-D}\right)\\ =\frac{1}{2}bB\left(\frac{B}{D}+\frac{B}{x\left(1-p-D/x\right)}\right)=\frac{1}{2}b{B}^2\left(\frac{1}{D}+\frac{1}{x\left(1-p-D/x\right)}\right)\\ \end{array}$$

(5)

The holding cost per cycle, TH, can be formulated as

$$\begin{array}{c}TH=h\left\{\frac{1}{2}\left(2y-\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}\right)t_3+\frac{1}{2}\left(y-\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}+py\right)\left(t_1-t_3\right)+py{t}_2\right\}\\ =\frac{1}{2}h\left\{y{t}_3-py{t}_3+\left(y-\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}+py\right)t_1+2py{t}_2\right\}\\ =\frac{1}{2}h\left\{\left(1-p\right)y{t}_3+\left(y-\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}+py\right)t_1+2py{t}_2\right\}\\ =\frac{1}{2}h\left\{\left(1-p\right)y\left(\frac{B}{x\left(1-p\right)-D}\right)+\left(\left(1+p\right)1-y-\frac{Bx\left(1-p\right)}{x\left(1-p\right)-D}\right)\left(\frac{y\left(1-p\right)-B}{D}\right)+2py\frac{B}{D}\right\}\\ =\frac{1}{2}h\left\{\frac{By}{x}\left(\frac{1-p}{1-p-\frac{D}{x}}\right)+\frac{y^2\left(1-p^2\right)}{D}-\frac{yB\left(1+p\right)}{D}-\frac{By{\left(1-p\right)}^2}{D\left(1-p-\frac{D}{x}\right)}+\frac{B^2\left(1-p\right)}{D\left(1-p-\frac{D}{x}\right)}+\frac{2pyB}{D}\right\}\\ \end{array}$$

(6)

In addition, the revenue per cycle received by selling perfect items, TR, is

$$TR=y\left(1-p\right)s$$

(7)

Finally, the net profit per cycle, TP(B, y), can be calculated by

$$\begin{array}{c}TP\left(B,y\right)=TR-\left(TK+TS+TD+TB+TH\right)=\left(1-p\right)ys-K-\left(1-p\right)yc-dy\\ -\frac{1}{2}h\left(\frac{By}{x}\left(\frac{1-p}{1-p-\frac{D}{x}}\right)+\frac{y^2\left(1-p^2\right)}{D}-\frac{yB\left(1+p\right)}{D}-\frac{By{\left(1-p\right)}^2}{D\left(1-p-\frac{D}{x}\right)}+\frac{B^2\left(1-p\right)}{D\left(1-p-\frac{D}{x}\right)}+\frac{2pyB}{D}\right)\\ -\frac{1}{2}b{B}^2\left(\frac{1}{D}+\frac{1}{x\left(1-p-\frac{D}{x}\right)}\right)\\ \end{array}$$

(8)

Based on Eq. 8, the expected profit per cycle is

$$\begin{array}{c}E\left[TP\left(B,y\right)\right]=\left(1-E\left[p\right]\right)ys-K-\left(1-E\left[p\right]\right)yc-dy\\ -\frac{1}{2}h\left(\frac{By}{x}E\left[\frac{1-p}{1-p-\frac{D}{x}}\right]+\frac{y^{2}E\left[1-p^2\right]}{D}-\frac{yB\left(1+E\left[p\right]\right)}{D}-\frac{By}{D}E\left[\frac{\left(1-p\right){11)}^2}{1-p-\frac{D}{x}}\right]+\frac{B^2}{D}\text{E}\left[\frac{1-p}{1-p-\frac{D}{x}}\right]+\frac{2E\left[p\right]yB}{D}\right)\\ -\left(\frac{b{B}^2}{2D}+\frac{b{B}^2}{2x}\text{E}\left[\frac{1}{1-p-\frac{D}{x}}\right]\right)\\ \end{array}$$

(9)

Since the process of generating the profit is renewal with renewal points at order placement, and the reward received at the end of each cycle is dependent on the duration of each cycle, the renewal-reward theorem could be used to calculate expected profit per unit time. The basic tools that are used are the computation of the reward per unit of time and the rate of the expected value of the reward.

Now, according to the renewal theorem, $\frac{E\left[TP\left(B,y\right)\right]}{E\left(T\right)}$ is the expected profit per unit time. As the expected cycle time E[T] is $\frac{\left(1-E\left[p\right]\right)y}{D}$, the expected profit per time, $E\left[TPU\left(B,y\right)\right]$, is

$$\begin{array}{c}E\left[TPU\left(B,y\right)\right]=Ds-\\ \left\{\frac{DK}{\left(1-E\left[p\right]\right)y}+Dc+\frac{dD}{\left(1-E\left[p\right]\right)}+\frac{h}{2}\left\{\frac{BD}{x\left(1-E\left[p\right]\right)}\text{E}\left[\frac{1-p}{1-p-\frac{D}{x}}\right]+\frac{yE\left(1-p^2\right)}{\left(1-E\left[p\right]\right)}-\frac{B\left(1+E\left[p\right]\right)}{\left(1-E\left[p\right]\right)}\right.\right.\\ \left.-\frac{B}{\left(1-E\left[p\right]\right)}E\left[\frac{\left(1-p\right){11)}^2}{1-p-\frac{D}{x}}\right]+\frac{B^2}{\left(1-E\left[p\right]\right)y}\text{E}\left[\frac{1-p}{1-p-\frac{D}{x}}\right]+\frac{2BE\left[p\right]}{\left(1-E\left[p\right]\right)}\right\}\\ \left.+\left(\frac{b{B}^2}{2\left(1-E\left[p\right]\right)y}+\frac{Db{B}^2}{2x\left(1-E\left[p\right]\right)y}\text{E}\left[\frac{1}{1-p-\frac{D}{x}}\right]\right)\right\}\\ \end{array}$$

(10)

Assuming $A_1=E\left[\frac{\left(1-p\right)}{\left(1-p-\frac{D}{x}\right)}\right],A_2=E\left[\frac{{\left(1-p\right)}^2}{\left(1-p-\frac{D}{x}\right)}\right],and{A}_3=E\left[\frac{1}{\left(1-p-\frac{D}{x}\right)}\right]$, Eq. 10 is reduced to

$$\begin{array}{c}E\left[TPU\left(B,y\right)\right]=Ds-\left\{\frac{DK}{\left(1-E\left[p\right]\right)y}+Dc+\frac{dD}{\left(1-E\left[p\right]\right)}\right.+\frac{h}{2}\left\{\frac{BD{A}_1}{x\left(1-E\left[p\right]\right)}+\frac{yE\left(1-p^2\right)}{\left(1-E\left[p\right]\right)}-\frac{B\left(1+E\left[p\right]\right)}{\left(1-E\left[p\right]\right)}\right.\\ \left.-\frac{B{A}_2}{\left(1-E\left[p\right]\right)}+\frac{B^2{A}_1}{\left(1-E\left[p\right]\right)y}+\frac{2BE\left[p\right]}{\left(1-E\left[p\right]\right)}\right\}\left.+\left(\frac{b{B}^2}{2\left(1-E\left[p\right]\right)y}+\frac{Db{B}^2{A}_3}{2x\left(1-E\left[p\right]\right)y}\right)\right\}\\ \end{array}$$

(11)

Equations 12 and 13 are the first and the second derivatives of E[TPU (B, y)] with respect to B, respectively

$$\begin{array}{c}\frac{\mathit{\partial }E\left[TPU\left(B,y\right)\right]}{\mathit{\partial }B}=-\frac{bB}{\left(1-E\left[p\right]\right)y}-\frac{BbD{A}_3}{x\left(1-E\left[p\right]\right)y}+\frac{h\left(1+E\left[p\right]\right)}{2\left(1-E\left[p\right]\right)}+\frac{h{A}_2}{2\left(1-E\left[p\right]\right)}-\frac{Bh{A}_1}{y\left(1-E\left[p\right]\right)}\\ -\frac{hE\left[p\right]}{\left(1-E\left[p\right]\right)}-\frac{Dh{A}_1}{2x\left(1-E\left[p\right]\right)}\\ \end{array}$$

(12)

$$\frac{{\mathit{\partial }}^{2}E\left[TPU\left(B,y\right)\right]}{{\mathit{\partial }}^{2}B}=-\frac{b}{\left(1-E\left[p\right]\right)y}-\frac{bD{A}_3}{x\left(1-E\left[p\right]\right)y}-\frac{h{A}_1}{y\left(1-E\left[p\right]\right)}$$

(13)

In addition, the first and the second derivatives of E[TPU (B, y)] with respect to y are obtained, respectively, in Eqs. 14, 15.

$$\frac{\mathit{\partial }E[TPU(B,y)]}{\mathit{\partial }y}=\frac{KD}{(1-E[p])y^2}+\frac{b{B}^2}{2(1-E[p])y^2}+\frac{b{B}^2{A}_{3}D}{2x(1-E[p])y^2}-\frac{1}{2}h\frac{E{(1-p)}^2}{(1-E[p])}+\frac{h{B}^2{A}_1}{2y^2(1-E[p])}$$

(14)

$$\frac{{\mathit{\partial }}^{2}E\left[TPU\left(B,y\right)\right]}{{\mathit{\partial }}^{2}y}=-\frac{2DK}{\left(1-E\left[p\right]\right)y^3}-\frac{b{B}^2}{\left(1-E\left[p\right]\right)y^3}-\frac{b{B}^2{A}_{3}D}{x\left(1-E\left[p\right]\right)y^3}-\frac{h{B}^2{A}_1}{y^3\left(1-E\left[p\right]\right)}$$

(15)

Equation 16 is used to show that there exist unique solutions of B and y.

$$\begin{array}{c}\left(\frac{{\mathit{\partial }}^{2}E\left[TPU\left(B,y\right)\right]}{{\mathit{\partial }}^{2}B}\times \frac{{\mathit{\partial }}^{2}E\left[TPU\left(B,y\right)\right]}{{\mathit{\partial }}^{2}y}\right)-{\left(\frac{{\mathit{\partial }}^{2}E\left[TPU\left(B,y\right)\right]}{\mathit{\partial }B\mathit{\partial }y}\right)}^2\\ =\frac{2KDb{x}^2+2b{D}^{2}Kx{A}_3+2DK{x}^{2}h{A}_1}{x^2{\left(1-E\left[p\right]\right)}^2{y}^4}\\ \end{array}$$

(16)

As $p<1-\frac{D}{x}$, both Eqs. 13 and 15 are negative and hence Eq. 16 becomes positive. This indicates that there exist unique solutions of B and y that maximize the annual profit.

Equating Eq. 12 to zero, the optimal B is obtained by

$$B^{\ast }=R{y}^{\ast }$$

(17)

where

$$R=\frac{hx\left(1-E\left[p\right]\right)+hx{A}_2-hD{A}_1}{2xb+2bD{A}_3+2hx{A}_1}$$

(18)

by substituting Eq. 17 into Eq. 14 and equating it to zero, the optimal y is determined by

$$y^{\ast }=\sqrt{\frac{2xKD}{hxE\left(1-p^2\right)-b{R}^{2}x-b{R}^2{A}_{3}D-hx{R}^2{A}_1}}$$

(19)

In the next section, numerical examples are solved to demonstrate the applicability of the proposed modeling.

Numerical examples

In order to compare the proposed model with the one in Hsu and Hsu’s (2012), numerical examples based on a uniform distribution for the percentage defective shown in Eq. 20 are provided in this section.

$$f\left(p\right)=\left\{\begin{array}{c}\frac{1}{\mathit{\beta }},0<p<\mathit{\beta }\hfill \\ 0,\text{otherwise}\hfill \end{array}\right.$$

(20)

The resulting equation follows:

$$A_1=E\left[\frac{(1-p)}{\left(1-p-\frac{D}{x}\right)}\right]=\underset{0}{\overset{\mathit{\beta }}{\int }}\frac{1-p}{1-p-\frac{D}{x}}f(p)dp=\underset{0}{\overset{\mathit{\beta }}{\int }}\frac{1}{\mathit{\beta }}\left[1+\frac{\frac{D}{x}}{1-p-\frac{D}{x}}\right]dp=1+\frac{D}{\mathit{\beta }x}ln\left(\frac{1-\frac{D}{x}}{1-\frac{D}{x}-\mathit{\beta }}\right)$$

(21)

$$A_2=E\left[\frac{{\left(1-p\right)}^2}{\left(1-p-\frac{D}{X}\right)}\right]=\underset{1-D/X-\mathit{\beta }}{\overset{1-D/X}{\int }}\frac{{\left(z+D/X\right)}^2}{z}f\left(z\right)dz=\underset{1-D/X-\mathit{\beta }}{\overset{1-D/X}{\int }}\frac{1}{\mathit{\beta }}\left(z+2D/x+\frac{{\left(D/x\right)}^2}{z}\right)dz=1-\frac{D}{x}-\frac{\mathit{\beta }}{2}+2\frac{D}{x}+\frac{1}{\mathit{\beta }}{\left(\frac{D}{x}\right)}^{2}ln\left(\frac{1-D/x}{1-D/x-\mathit{\beta }}\right)=1+\frac{D}{x}-\frac{\mathit{\beta }}{2}+\frac{1}{\mathit{\beta }}{\left(\frac{D}{x}\right)}^{2}ln\left(\frac{1-D/x}{1-D/x-\mathit{\beta }}\right)$$

$$A_3=E\left[\frac{1}{\left(1-p-\frac{D}{X}\right)}\right]=\frac{1}{\mathit{\beta }}ln\left(\frac{1-D/x}{1-D/x-\mathit{\beta }}\right)$$

(22)

$$E\left[p\right]=\underset{0}{\overset{\mathit{\beta }}{\int }}pf\left(p\right)dp=\underset{0}{\overset{\mathit{\beta }}{\int }}\frac{p}{\mathit{\beta }}dp=\frac{\mathit{\beta }}{2}$$

(23)

$$E\left(1-p^2\right)=\underset{0}{\overset{\mathit{\beta }}{\int }}\left(1-p^2\right)\frac{1}{\mathit{\beta }}dp={\left.\frac{1}{\mathit{\beta }}\left(p-\frac{p^3}{3}\right)\right]}_0^{\mathit{\beta }}=1-\frac{{\mathit{\beta }}^2}{3}$$

(24)

Tables 12, 3, and 4 show the optimal values of B and y of the proposed model that is compared to the ones of the Hsu and Hsu (2012) model in various scenarios. The scenarios are chosen based on different screening rates, percentage defective distributions, holding costs and backordering cost. More specifically, in Table 1, β = 0.04; D = 50,000; k = 100; h = 5; b = 10; d = 0.5; c = 25; s = 50 and x varies from 75,000 to 175,200. In Table 2, p is uniformly distributed between 0 and β that varies between 0.04 and 0.5, D = 50,000, x = 175,200, K = 100, h = 5, b = 10, d = 0.5, c = 25, s = 50. In Table 3, β = 0.04, D = 50,000, x = 175,200, K = 100, b = 10, d = 0.5, c = 25, s = 50 and h varies between 1 and 10. In Table 4, D = 50,000, x = 175200, K = 100, h = 5, β = 0.04, d = 0.5, c = 25, s = 50 and b is between 5 and 20.

Table 1 Comparison results based on different screening rates

Table 2 Comparison results based on different parameters of the percentage defective distribution

Table 3 Comparison results based on different holding costs

Table 4 Comparison results based on different backordering costs

The results in all tables show that the policy that is presented in this paper has resulted in better solutions. In other words, keeping the defective items in the warehouse and returning them back to the supplier results in more expected profit than the one obtained based on selling the defective items at a lower price.

Conclusion

This paper extended the model originally presented by Wee et al. (2007) and corrected by Hsu and Hsu (2012). In Wee et al. (2007) model, the defective items are sold at a lower price right after the screening process. In this paper, however, the defective items are stored in the warehouse until the next delivery is received and then are returned back to the supplier via the supplier’s vehicle. After deriving optimal order and backordering quantities using the renewal-reward theorem, the results of some numerical examples indicated that the new policy are more lucrative for the retailer in the specific examples compared with Hsu and Hsu’s (2012) model. Although the new policy caused holding cost to increase, the retailer only purchased and sold perfect items where there was no loss due to receiving damaged items.

Author contribution

BMV, STAN, MF, and MEMR used the renewal-reward theorem to derive closed-form equations for the optimal order and shortage quantities of batches that contain defective items with percentage nonconforming following a certain probability density function. In this newly defined inventory problem, the orders delivered to a retailer are subject to 100 % screening process at a rate higher than the demand rate. Shortage is backordered and defective items in each ordering cycle are stored in a warehouse to be returned to the supplier when a new order is received. Although the retailer does not sell defective items at a lower price and only trades perfect items (to avoid loss), a higher holding cost incurs to store defective items. The novelty comes from the fact that there has not been any closed-form equation proposed in the literature to determine the optimal order and shortage quantities of returnable imperfect items in a single supplier-single retailer supply chain. This research has a broad application in many inventory control problems in which, the ordered imperfect items can be returned to the supplier.