A novel hybrid genetic algorithm to solve the make-to-order sequence-dependent flow-shop scheduling problem

Abstract

Flow-shop scheduling problem (FSP) deals with the scheduling of a set of n jobs that visit a set of m machines in the same order. As the FSP is NP-hard, there is no efficient algorithm to reach the optimal solution of the problem. To minimize the holding, delay and setup costs of large permutation flow-shop scheduling problems with sequence-dependent setup times on each machine, this paper develops a novel hybrid genetic algorithm (HGA) with three genetic operators. Proposed HGA applies a modified approach to generate a pool of initial solutions, and also uses an improved heuristic called the iterated swap procedure to improve the initial solutions. We consider the make-to-order production approach that some sequences between jobs are assumed as tabu based on maximum allowable setup cost. In addition, the results are compared to some recently developed heuristics and computational experimental results show that the proposed HGA performs very competitively with respect to accuracy and efficiency of solution.

Introduction

It is almost seven decades that flow-shop scheduling problems (FSP) have been studied as a major field of study in manufacturing researches. In an m machine flow shop, there are m stages in series with one or more machines at each. Also, there are n jobs that each one has to be processed in each of the m stages in the same order. In the classical flow-shop problem, there is one machine at each stage and this field attracts the most attendances. Two major sub-problems of FSP are sequence-independent setup time (SIST) and sequence-dependent setup time (SDST). The SDST flow-shop problem is more compatible with the real-world problem, but has attracted much less attention, especially before 2000 (Allahverdi et al. 2008).

The objective in flow-shop scheduling problems is to find a sequence for processing the jobs on the machines so that a given criterion is optimized. This yields a total of n! possible orderings of the operations on each machine, and a total of (n!) × m possible processing sequences. Flow-shop scheduling researches usually only attend permutation sequences where the processing order of operations is the same for all machines. Here, we also adopt this restriction.

Minimizing the maximum completion time across all jobs (also called make-span and denoted by C_max) is the most well-known and applicable criterion in the literature. Regarding the computational complexity, the SDST flow-shop with the C_max objective has been shown to be NP-hard by Gupta and Darrow (1986), even when m = 1 and also when m = 2 and setups are presented only on the first or second machine. Therefore, solving the problem by an exact algorithm is time consuming and computationally intractable.

Pioneering work was due to Johnson (1954) who proposed a simple rule to obtain optimal sequences for the permutation flow-shop problem (PFSP) with two machines. This work was the starting point of several attempts for solving the PFSP with more than two machines. Because of NP completeness of the PFSP (Garey et al. 1976; Campbell et al. 1970), researchers have mainly attempted to the development of effective heuristics and meta-heuristics. Some of the first heuristic methods in this field are the well-known NEH heuristic by Nawaz et al. (1983) and the genetic algorithm of Reeves (1995).

After 2000, there are wide range of heuristics, meta-heuristics and hybrid meta-heuristics developed for flow-shop and permutation flow-shop by researchers. Ruiz et al. (2005) proposed two heuristics for the same problem, and showed that their heuristics outperform previous ones. Ruiz and Stutzle (2008) presented two simple local search-based iterated greedy algorithms, and showed that their algorithms perform better than those of Ruiz et al. (2005). Tseng et al. (2005) developed a penalty-based heuristic algorithm for the same problem and compared their heuristic with an existing index heuristic algorithm. Among all approaches, one of the most successful meta-heuristics to solve PFSP from last until now is genetic algorithm. Like one worked by Reeves (1995) and Sun and Hwang (2001). Sun and Hwang (2001) addressed a related problem of F₂/ST_sd/C_max where the setup times are present only on the second machine, and the setup time of a job depends on k (k > 1) immediately preceding jobs. They proposed a dynamic programming formulation and a genetic algorithm for the problem. Chaari et al. (2011) considered a scheduling problem under uncertainty. They developed a genetic algorithm for the case of hybrid flow-shop scheduling problem that the processing time of each job for each machine at each stage is the source of uncertainty. They defined a robust bi-objective evaluation function to obtain a robust, effective solution that is only slightly sensitive to data uncertainty. Tseng and Lin (2010) proposed a hybrid genetic algorithm to solve the no-wait flow-shop scheduling problem with the make-span objective. The proposed algorithm hybridized the genetic algorithm and a novel local search scheme. The proposed local search scheme combines two local search methods: the insertion search and a novel local search method called the insertion search with cut-and-repair. Jarboui et al. (2011) proposed a hybrid genetic algorithm to minimize the make-span and the total flow time in the no-wait flow-shop scheduling problem. In their research, the variable neighborhood search was used as an improvement procedure in the last step of the genetic algorithm. Huang and Huang (2010) considered a flow-shop scheduling problem with synchronous material movement in an automated machine center consisting of a loading/unloading (L/U) station, m processing machines, and a rotary table. Furthermore, other useful and strong approaches can be fined to solve PFSP. Li et al. (2004) presented partial enumeration method (PEM) to minimize the make-span performance of large flow-shop scheduling problems. The PEM run in short time and could easily combine with other algorithms or rules to improve performance. In their research, two priority rules, variance method and variance–mean method were developed. Laha and Chakraborty (2007) developed an efficient stochastic hybrid heuristic (H3) for flow-shop scheduling problem and showed the superiority of their work against other researches. Noori-Darvish and Tavakkoli-Moghaddam (2012) proposed a novel bi-objective mathematical programming for an open-shop scheduling problem with setup and processing times separately such that not only the setup times are dependent on the machines, but also they are dependent on the sequence of jobs that should be processed on a machine. They minimized the total tardiness and the make-span. Maleki-Darounkolaei et al. (2012) considered a three-stage assembly flow-shop scheduling problem with sequence-dependent setup times at the first stage and blocking times between each stage in such a way that the weighted mean completion time and make-span are minimized. Finally, Sheibani (2010) described a polynomial-time heuristic (PH) for the permutation flow-shop scheduling problem with the make-span criterion. His method consists of two phases: arranging the jobs in priority order and then constructing a sequence. He employed a fuzzy greedy evaluation function to prioritize the jobs for incorporating into the construction phase of the heuristic.

Successful applications of GA to solve NP-hard problems such as FSP stimulated us to develop one hybrid GA (HGA) to deal with the problem efficiently and effectively.

As mentioned before in the classical flow-shop problem, the make-span minimization criterion has always attracted the attention of researchers. With a fast glance to the real-world situations, we can see that due date and setup costs are the most important criteria in production planning, especially in the make-to-order situation. Various customers offered their orders (jobs) and each order has its own due date, holding cost and delay cost, and just focus on the make-span is not an effective attempt. Almost all real-world problems are multi-criteria and considering just one criterion is too far from real situations (Mirabi 2010). Allahverdi et al. (2008) implied that almost no multi-criteria researches are available according to real situations. He also suggested the due date-related criteria for more consideration.

As mentioned before, SDST is more adaptable with real situations. Furthermore, in wide cases there are some infeasible sequences (Tabu sequences) based on setup cost. For example, in the dyeing process of all kinds of fibers, each basket filled by wet fiber (job) must be dyed by several dyeing machines (stages). Dyeing completely the bright color (cream, white) after completely the dark color (black, blue and red) caused high setup costs (after dark color, each machine must be cleaned carefully for almost 2 days and also at least one batch of bright color waste for the reason of remain dyes from dark color) and they are considered as infeasible sequences. These are the same conditions used in the cable industry for producing colored wires.

In this research, we attend the permutation flow shop that must process n jobs, each one received from specific customer. Each job has specific due date and delay cost. Setup time and setup cost are sequence dependent and also objective function constructs by three criteria as delay, holding and setup costs. Also, some sequences known as Tabu based on yielded setup costs. This situation is compatible with the large category of the real-world problems, and is completely missed in the literature. We develop one HGA to solve the problem.

The paper is organized as follows: Section 2 discusses the principles of the algorithms used to solve the permutation FSP. Section 3 compares the performance of the algorithms. Finally, Sect. 4 concludes the paper.

Hybrid genetic algorithm

In this research, genetic algorithm (GA) is applied to solve permutation flow-shop scheduling problem. John Holland proposed GA in the 1960s for the first time. GA categorizes as a class of evolutionary algorithms (EA), which generate solutions to optimization and heuristic problems by techniques inspired by natural evolution, such as mutation, selection, and crossover. The main concept of GA is to evolve a population of candidate solutions (called individuals, creatures, or phenotypes) to an optimization problem toward better solutions. Today, GA has wide and successful applications to solve hard optimization problems. The success is mainly due to its easy to understand and operation and great flexibility. These reasons stimulate us to use this strong approach to solve the presented problem.

Initially, many individual solutions (called chromosomes) are (usually) randomly generated to generate an initial population. The population size depends on the nature of the problem, but generally contains several hundreds or thousands of possible solutions. The chromosomes evolve through successive iterations, called generations. During each generation, the chromosomes are evaluated through a fitness-based process where fitter solutions (as measured by a fitness function) are typically more likely to be selected. The next step is to generate a second-generation population of solutions from those selected through genetic operators: crossover and mutation.

For each new solution to be produced, a pair of “parent” solutions is selected for breeding from the pool selected previously. By producing a “child” solution using the above methods of crossover and mutation, a new solution is created which typically shares many of the characteristics of its “parents”. New parents are selected for each new child, and the process continues until a new population of solutions of appropriate size is generated.

After a fixed number of generations, the algorithm converges to the best chromosome, which probably is the optimal solution or may be a near-optimal solution of the problem.

Flow-shop scheduling problem can be regarded as a hard optimization problem and to enrich the capability of the proposed GA in this paper it is hybridized with some other approaches. The GA developed in this paper is hybridized with several heuristics to improve the solution further.

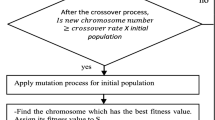
Figure 1 shows the flowchart of HGA for the FSP. HGA hybridized with an improved heuristic called the iterated swap procedure (ISP). Besides the ISP, it also hybridized the heuristic method to construct a pool of initial solutions. Also, the author uses three genetic operators to make a good new offspring.

Fig. 1

The flowchart of the HGA

The procedure of the HGA is described as follows: After the GA parameters, such as the iteration number, the population size ($P_{\text{size}}$), the crossover rate, and the mutation rate, have been set, the HGA generates the initial chromosomes of the problem. After the predetermined number of initial chromosomes is generated, the ISP is adopted to improve all chromosomes. Each chromosome is then measured by an evaluation function. The roulette wheel selection operation is adopted to select some chromosomes for the genetic operations, including the order crossover, the heuristic mutation, and the inversion mutation. After a new chromosome or offspring is produced, its links are improved by the ISP. The fitness of the offspring is measured and the offspring may become a member of the population if it possesses a relatively good quality. These steps form iteration, and then the roulette wheel selection is performed again to start the next iteration. The HGA will not stop unless the predetermined number of iterations is conducted.

Initialization

The initial solution for HGA is ideally generated by a high performance construction heuristic. In the initialization phase, we need one pool of initial solutions and based on our experience, construction heuristic works better that random approach. Before all, we construct a list of Tabu sequences based on earned information about setup costs. After that, we classify all orders (jobs) in four levels based on their importance. Importance of each job is determined by its customer importance and ranking (based on ISO standard list), job delay cost, job holding cost and other factors based on the management viewpoint. Levels names are low, medium, high and very high. Jobs in very high level have the most importance and jobs in low level have the least.

Each job has its own due date and by delivering before and after due date, holding and delay cost per unit of period must be paid, respectively. For example, assumed delivery time of job numbered 1 is period 4, and the process time is two periods. Also assumed holding cost and delay cost per period is 4 and 8, and planning horizon has 10 time periods. For job 1, we can construct a string like Fig. 2.

Fig. 2

String related to job 1

It means produce job 1 in period 1 costs 8 and so on. For n jobs we have n strings like this. For initialization the following algorithm is used:

• 1) Input T (number of time period) n (number of Job) and $P_{\text{size}}$ (population size)

• 2) Numbered jobs from 1 to n and time periods from 1 to T

• 3) For t = 1 to T

• 4) t = 1

• 5) Select a job with the least cost in period t and put it as soon as possible in the list of sequence. If two jobs have the same cost, select a job with more importance and with the same conditions select one in random

• 6) Eliminate the string related to selected job

• 7) If there is free capacity in period t go to 4

• 8) If not t = t + 1

• 9) End for

• 10) Extract final sequence (initial solution 1)

• 11) For k = 1 to $P_{\text{size}}$

• 12) Interchange the position of two jobs in the same level (by random)

• 13) If there is no Tabu sequence, finalize the result as one initial solution

• 14) End for

• 15) Extract all $P_{\text{size}}$ initial solutions

Of course in the initialization phase, we do not consider the setup cost and just care about Tabu sequences.

Improvement

The 2-opt local search heuristic is generally used to improve the solutions of the hard optimization problems. However, it increases the computational time because every two swaps are examined. If a new solution generated is better than the original one, or parent, in terms of quality, it will replace and become the parent. All two swaps are examined again until there is no further improvement in the parent. To increase efficiency, the ISP (Ho and Ji 2003, 2004) shown in Fig. 3, is used to improve the links of each initial solution and each offspring generated by the three genetic operators. The principle of the ISP is similar to that of the 2-opt local search heuristic, except that some instead of all two swaps are examined. The procedure of the ISP is as follows:

Fig. 3

The iterated swap procedure

• Step 1: Select two genes randomly from a link of a parent.

• Step 2: Exchange the positions of the two genes to form an offspring.

• Step 3: Swap the neighbors of the two genes to form four more offspring.

• Step 4: Evaluate all offspring and find the best one.

• Step 5: If the best offspring is better than the parent, replace the parent with the best offspring and go back to Step 1; otherwise, stop.

Evaluation

As mentioned before, the fitness function is minimizing the tardiness, holding, and setup costs (Mirabi 2010). For example, consider one solution from pool of solutions (called solution h). Fitness function of this selected solution is:

$$\begin{array}{c}Z\left(h\right)=\sum _{j=0}^n\sum _{i=1}^{n}S{C}_{ij}\left(\sum _{j=0}^n{X}_{jit}\right)+\sum _{i=1}^n\sum _{t={\text{DD}}_i+1}^n\left(\sum _{j=0}^n{X}_{jit}\times (t-{\text{DD}}_i)\times {\text{DC}}_i\right)+\\ \sum _{j=1}^n\sum _{t=\text{min}\{{\text{RT}}_i,{\text{DD}}_i\}}^{{\text{DD}}_i}\left(\sum _{j=0}^n{X}_{jit}\times ({\text{DD}}_i-t)\times {\text{HC}}_i\right)\\ \end{array}$$

where indices i and j = 1,…,n index set of all jobs, t = 1,…,T index set of all periods. All periods are assumed to be of equal length; parameters: PT _i is processing time of job i, DD _i due date of job i, ST_0i initial setup time of job i (when job i is the first job in sequence), ST _ji is setup time of job i when it is processed after job j, SC_0i is initial setup cost of job i (when job i is the first job in sequence), SC _ji is setup cost of job i when it process after job j, HC _i is holding cost of job i per each time period, DC _i is delay cost of job i per each time period, RT _i is release time of job i; variables: X _jit 1, if sequence ji (job i is processed after job j) appears in period t; 0, otherwise; X_0i1 1, if job i is the first job in sequence (obviously it produce in period 1); 0, otherwise.

The first term of the fitness function calculates the sum of all setup costs for each ji (ij) sequence in the production line. Second term shows that if each job i is produced after due date (), for each delay period, the penalty in accordance to DC_i should be paid. Finally, the last term mention producing after due date impose the delay cost.

In this research, we just work with the fitness function, but there are some constraints for the problem that we refer readers to Mirabi (2010).

Selection

The commonly used genetic operator is the roulette wheel selection operation (Goldberg 1989). It is the proportionate reproduction operator where a string is selected for the mating pool with a probability proportional to its fitness. Thus, the ith string in the population is selected with a probability proportional. The fitter is the chromosome, the higher is the probability of being selected. Although one chromosome has the highest fitness, there is no guarantee it will be selected. Since the population size is usually kept fixed in a simple GA, the sum of the probability of each string being selected for the mating pools must be 1. Suppose the population size is P_size, then the selection procedure is as follows:

• Step 1: Calculate the total fitness of the population:

• $$F=\sum _{h=1}^{P_{\text{size}}}Z(h)$$

• Step 2: Calculate the selection probability $P_h$ for each chromosome X _h :

• $$P_h=\frac{F-Z(h)}{F\ast \left(P_{\text{size}}-1\right)}h=1,2,\dots ,P_{\text{size}}$$

• Step 3: Calculate the cumulative probability Q _h for each chromosome $X_h$:

• $$Q_h=\sum _{j=1}^h{P}_{j}h=1,2,\dots ,P_{size}$$

• Step 4: Generate a random number r in the range (0, 1].

• Step 5: If $Q_{h-1}<r\le Q_h$, then chromosome $X_h$ is selected.

Genetic operation

The genetic search progress is obtained by two essential genetic operations, including exploitation and exploration. Generally, the crossover operator exploits a better solution while the mutation operator explores a wider search space. The genetic operators used in the algorithms for the flow-shop problem are one crossover and two mutations, which are called the heuristic mutation and the inversion mutation, respectively.

The order crossover

The crossover operator adopted in the HGA is the classical order crossover (Gen and Cheng 1997), and two offsprings will be generated at each time. The procedure of the order crossover operation is:

• Step 1: Select a substring from the first parent randomly.

• Step 2: Produce an offspring by copying the substring into the corresponding positions in the offspring.

• Step 3: Delete those genes in the substring from the second parent. The resulting genes form a sequence.

• Step 4: Place the genes into the unfilled positions of the offspring from left to right according to the resulting sequence of genes in Step 3 to produce an offspring, shown in Fig. 4.

  Fig. 4

  

  The order crossover operator

• Step 5: Repeat Steps 1–4 to produce another offspring by exchanging the two parents.

The heuristic mutation

A heuristic mutation (Gen and Cheng 1997) is designed with the neighborhood technique to produce a better offspring. A set of chromosomes transformed from a parent by exchanging some genes is regarded as the neighborhood. Only the best one in the neighborhood is used as the offspring produced by the mutation. However, the purpose of the mutation operation is to promote diversity of the population. Therefore, it is necessary to change the original heuristic mutation for the FSP. The modification is that all neighbors generated are used as the offspring. The procedure of the heuristic mutation operation, shown in Fig. 5, is taken as follows:

Fig. 5

The heuristic mutation operator

• Step 1: Pick up three genes in a parent at random.

• Step 2: Generate neighbors for all possible permutations of the selected genes, and all neighbors generated are regarded as the offspring.

The inversion mutation

The inversion operator (Gen and Cheng 1997), shown in Fig. 6, selects a substring from a parent and flips it to form an offspring. However, the inversion operator works with one chromosome only. It is similar to the heuristic mutation and thus lacks the interchange of characteristics between chromosomes. Therefore, the inversion operator is a mutation operation, which is used to increase the diversity of the population rather than to enhance the quality of the population.

Fig. 6

The inversion mutation operator

Result analysis

In this section, a computational study is carried out to compare the HGA with three best recently developed heuristics. We mean PEM presented by Li et al. (2004); H3 developed by Laha and Chakraborty (2007) and PH described by Sheibani (2010). Four methods are compared using different problem sizes (n = 10, 20, 30, 40, 50, 100 and m = 5, 10, 15, 20). For each class of the problem defined by given (n, m), ten instances of problem are randomly generated. Thus, we obtain a total of 280 problem instances. Processing time and setup time are given from uniform random U(1, 99) and U(1, 9) discrete distributions, respectively. The numerical results are averaged through each ten instances.

The parameters of the HGA for the problems are population size 20, crossover rate 0.5 and mutation rate 0.2.

Therefore, five pairs of chromosome are selected to perform the order crossover operation, whereas four chromosomes perform the heuristic mutation operation and the inversion mutation operation. The total number of offspring produced per iteration will be 34 (10 from the order crossover operation, 20 from the heuristic mutation operation, and 4 from the inversion mutation operation). The platform of the experiments is a personal computer with a Pentium-III 1.2 Hz CPU and 512 MB RAM. The programs are coded in MATLAB. Also to have equal condition between four methods all algorithms are run by the same iteration.

For evaluating the different algorithms, we used the performance measure (PM) for each class of problem stated as:

$${\text{PM}}_i=\frac{{\text{Solution}}_i-{\text{Best}}_{\text{sol}}}{{\text{Best}}_{\text{sol}}}$$

(1)

where Solution _i is the fitness value obtained by algorithm i, and Best_sol is the best fitness value between all algorithms.

The average, minimum, and maximum PM values for all algorithms are shown in Table 1. The columns labeled “Min” show, in subscript, the number of instances (between ten instances) for which the algorithm solution was equal to the corresponding Best_sol. In the “average” column, we showed two subcolumns including the average of ten PM values related to ten instances and also the average of ten solution times to reach all ten results. With respect to the solutions gained, Table 1 demonstrates that the algorithms have the rank of 1 for HGA, 2 for PH, 3 for H3, and 4 for PEM.

Table 1 PM values for comparison studies between algorithms (times are in second)

Now, for more detailed comparison, two algorithms of HGA and PH are considered. In this step, it is desired to stop both algorithms at the same CPU time. The value of this CPU time has taken the minimum CPU time between the two algorithms in Table 1. For example, the common CPU time for the first class of problem (n = 10, m = 5) is min (1.05, 1.83) = 1.05.

The author now tests the hypothesis that the population corresponding to the differences has mean μ zero; specifically, test the (null) hypothesis μ against the alternative μ > 0. It is assumed that the make-span difference is a normal variable, and choose the significance level α = 0.05. If the hypothesis is true, the random variable $T=({\overline{X}}_1-{\overline{X}}_2)/\sqrt{(S_1^2/n_1)+(S_2^2/n_2)}$ has a t distribution with: $\mathit{\upsilon }={(S_1^2/n_1+S_2^2/n_2)}^2/(\frac{{(S_1^2/n_1)}^2}{n_1-1}+\frac{{(S_2^2/n_2)}^2}{n_2-1})$ degrees of freedom (Mirabi 2010). The critical value of c is obtained from the relation $\text{Prob}(T>c)=\mathit{\alpha }=0.05$. For example, the first entry in Table 1 corresponds to the $\text{sample size}=n_1=n_2=10$, μ₀ = 0, sample means for HGA and H3 are ${\overline{X}}_1=759.38$ and ${\overline{X}}_2=766.46$, respectively. Sample standard deviations for HGA and H3 are $S_1=2.88$ and $S_2=2.55$, respectively. Since $t=1.73<T=5.81$, we conclude that the difference is statistically significant. Table 2 displays that HGA outperforms H3 in all class of problems except six (76 % superiority). More than 77 % of these superiorities are statistically significant.

Table 2 Detailed comparison between HGA and PH

Conclusions

In this paper, we studied the permutation flow-shop scheduling problem in sequence-dependent condition to challenge a large number of real-world problems in make-to-order production strategy. FSP is a hard optimization problem, and we develop one meta-heuristic approach based on genetic algorithm called HGA to solve it. Genetic algorithm hybridized with an improved heuristic called the iterated swap procedure (ISP). Besides the ISP, it hybridized the heuristic approach to construct a pool of initial solutions. Also, we use three genetic operators to make a good new offspring. Computational results demonstrate the performance of presented method compared to some of the strong methods recently developed. It is noticeable when we see the most differences between HGA and the best method among considered approaches are also significant in the level of α = 0.05.