Simulation of Prestressed Steel Fiber Concrete Beams Subjected to Shear

Abstract

This paper developed an analytical software, called Simulation of Concrete Structures (SCS), which is used for numerical analysis of shear-critical prestressed steel fiber concrete structures. Based on the previous research at the University of Houston (UH), SCS has been derived from an object-oriented software framework called Open System for Earthquake Engineering Simulation (OpenSees). OpenSees was originally developed at the University of California, Berkeley. New module has been created for steel fiber concrete under prestress based on the constitutive relationships of this material developed at UH. This new material module has been integrated with the existing material modules in OpenSees. SCS thus developed has been used for predicting the behavior of the prestressed steel fiber concrete I-beams and Box-beams tested earlier in this research. The analysis could well predict the entire behavior of the beams including the elastic stiffness, yield point, post-yield stiffness, and maximum load for both web shear and flexure shear failure modes.

1 Introduction

OpenSees is an object-oriented computer program in seismic engineering (Fenves 2015). The features of OpenSees are described on the OpenSees website (www.opensees.berkeley.edu) and presented briefly here.

The architecture of OpenSees consists of four objects: ModelBuilder, Domain, Analysis, and Recorder under the OpenSees framework, as shown in Fig. 1.

Fig. 1

Principal objects in OpenSees (Fenves 2015).

The ModelBuilder object constructs the nodes and masses on the nodes, creates the elements and materials of the elements, defines the loads exerting on the nodes and the elements, and defines the constraints exerting on the nodes. The ModelBuilder is responsible for building the objects in the model such as Node, Mass, Material, Element, LoadPattern, Constraint, etc. and adding them to the Domain object.

After the objects are created by the ModelBuilder object, they are stored in the Domain object. The Domain object also provides access of Analysis and Recorder objects to the objects in the Domain and holds the state of the model during the analysis procedure.

The Analysis object is responsible for performing static or dynamic analysis on the model (Fenves 2015). The OpenSees is not able to perform nonlinear analysis on membrane structures such as reinforced concrete panels and shear walls because there is no membrane model in it. Also, the uniaxial material models of steel and concrete in OpenSees are too simple, and more sophisticated models need to be created. For example, the concrete model Concrete01 in OpenSees does not consider the stress of concrete in tension and the softening effect in compression due to the biaxial stress status. The steel model Steel01 does not consider the Bauschinger effect in the reloading and unloading paths. Therefore, the new finite element models of reinforced concrete material could be installed into OpenSees for performing analysis on reinforced concrete membrane structures.

2 Softened Membrane Model for Prestressed Steel Fiber Concrete (SMM-PSFC)

SMM-PSFC (Hoffman 2010) was developed to simulate the entire behavior of PSFC elements under monotonic loading. SMM-PSFC consisted of the stress equilibrium and strain compatibility equations along with the constitutive models of materials. However, SMM-PSFC contains the uniaxial constitutive models of materials under monotonic loading only.

2.1 Stress Equilibrium and Strain Compatibility Equations

Figure 2 shows an in-plane element model. The element considered is reinforced with two orthogonal grids of prestressing tendons and mild steel bars. The first Cartesian $\ell - \, t$ coordinate system is along the steel bar directions. The second Cartesian 1–2 coordinates is along the principal stress. For the analytical purposes, it is assumed that the membrane element thickness is uniform with the steel bars are uniformly distributed in two orthogonal directions. The four applied stresses exerting on the element edges are assumed to be uniformly distributed.

Fig. 2

A typical reinforced concrete plane stress element.

In a membrane element, the external applied stresses ($\sigma_{\ell }$,$\sigma_{t}$ and $\tau_{\ell t}$) can be indicated by the prestressing steel stresses ($f_{\ell p}$ and $f_{tp}$), the mild steel stresses ($f_{\ell }$ and $f_{t}$), and the internal stresses of concrete ($\sigma_{2}^{c}$,$\sigma_{1}^{c}$ and $\tau_{21}^{c}$), the three stress equilibrium equations are given in Eqs. (1) to (3).

$$ \sigma_{\ell } = \sigma_{2}^{c} \cos^{2} \alpha_{2} + \sigma_{1}^{c} \sin^{2} \alpha_{2} + \tau_{21}^{c} 2\sin \alpha_{2} \cos \alpha_{2} + \rho_{\ell } f_{\ell } + \rho_{\ell p} f_{\ell p} $$

(1)

$$ \sigma_{t} = \sigma_{2}^{c} \sin^{2} \alpha_{2} + \sigma_{1}^{c} \cos^{2} \alpha_{2} - \tau_{21}^{c} 2\sin \alpha_{2} \cos \alpha_{2} + \rho_{t} f_{t} + \rho_{tp} f_{tp} , $$

(2)

$$ \tau_{\ell t} = ( - \sigma_{2}^{c} + \sigma_{1}^{c} )\sin \alpha_{2} \cos \alpha_{2} + \tau_{21}^{c} (\cos^{2} \alpha_{2} - \sin^{2} \alpha_{2} ) $$

(3)

The strains ($\varepsilon_{1}$, $\varepsilon_{2}$ and $\gamma_{21}$) in 1–2 coordinates can be converted to the strains ($\varepsilon_{\ell }$, $\varepsilon_{t}$ and $\gamma_{\ell t}$), as shown in Eqs. (4) to (6) (Pang and Hsu 1996).

$$ \varepsilon_{\ell } = \varepsilon_{2} \cos^{2} \alpha_{2} + \varepsilon_{1} \sin^{2} \alpha_{2} + \frac{{\gamma_{21} }}{2}2\sin \alpha_{2} \cos \alpha_{2} $$

(4)

$$ \varepsilon_{t} = \varepsilon_{2} \sin^{2} \alpha_{2} + \varepsilon_{1} \cos^{2} \alpha_{2} - \frac{{\gamma_{21} }}{2}2\sin \alpha_{2} \cos \alpha_{2} $$

(5)

$$ \frac{{\gamma_{\ell t} }}{2} = ( - \varepsilon_{2} + \varepsilon_{1} )\sin \alpha_{2} \cos \alpha_{2} + \frac{{\gamma_{21} }}{2}(\cos^{2} \alpha_{2} - \sin^{2} \alpha_{2} ) $$

(6)

2.2 Biaxial Strains Convert to Uniaxial Strains

Since general lab experiments and reference literatures can give only the uniaxial constitutive laws of steel and concrete, only the uniaxial constitutive laws can be utilized by a general analytical software, the biaxial strains in above equations should be transformed to uniaxial strains. Thus, using the Hsu/Zhu ratios ($\nu_{12}$,$\nu_{21}$), four equations has been derived (Zhu and Hsu 2002) to represent the relationship between the uniaxial strains ($\overline{{\varepsilon_{1} }} ,\overline{{\varepsilon_{2} }} ,\overline{{\varepsilon_{l} }}$ and $\overline{{\varepsilon_{t} }}$) and the biaxial strains ($\varepsilon_{1}$,$\varepsilon_{2}$,$\varepsilon_{\ell }$ and $\varepsilon_{t}$), as shown in Eqs. (7) to (10).

$$ \bar{\varepsilon }_{1} = \frac{1}{{1 - \nu_{12} \nu_{21} }}\varepsilon_{1} + \frac{{\nu_{12} }}{{1 - \nu_{12} \nu_{21} }}\varepsilon_{2} $$

(7)

$$ \bar{\varepsilon }_{2} = \frac{{\nu_{21} }}{{1 - \nu_{12} \nu_{21} }}\varepsilon_{1} + \frac{1}{{1 - \nu_{12} \nu_{21} }}\varepsilon_{2} $$

(8)

$$ \bar{\varepsilon }_{\ell } = \bar{\varepsilon }_{2} \cos^{2} \alpha_{2} + \bar{\varepsilon }_{1} \sin^{2} \alpha_{2} + \frac{{\gamma_{12} }}{2}2\sin \alpha_{2} \cos \alpha_{2} $$

(9)

$$ \bar{\varepsilon }_{t} = \bar{\varepsilon }_{2} \sin^{2} \alpha_{2} + \bar{\varepsilon }_{1} \cos^{2} \alpha_{2} - \frac{{\gamma_{12} }}{2}2\sin \alpha_{2} \cos \alpha_{2} $$

(10)

The uniaxial strains $\overline{{\varepsilon_{1} }} ,\overline{{\varepsilon_{2} }} ,\overline{{\varepsilon_{l} }}$ and $\overline{\varepsilon }_{t}$ can be calculated by Eqs. (7) to (10), then the stresses $\sigma_{1}^{c}$, $\sigma_{2}^{c}$, $\tau_{12}^{c}$, $f_{\ell }$ and $f_{t}$ in Eqs. (1) to (3) can be obtained using the uniaxial constitutive laws.

Under monotonic shear stresses, two Hsu/Zhu ratios of panels can be given in Eqs. (11) and (12) (Zhu and Hsu 2002).

$$ \nu _{{12}} = \left\{ {\begin{array}{*{20}c} {0.2 + 850\varepsilon _{{sf}} ,} & {\varepsilon _{{sf}} \le \varepsilon _{y} } \\ {1.9,} & {\varepsilon _{{sf}} > \varepsilon _{y} } \\ \end{array} } \right. $$

(11)

$$ \nu_{21} = 0 $$

(12)

Where, $\varepsilon_{sf}$ is the average (smeared) tensile strain of steel rebar in the $\ell -$ or the $t -$ direction, whichever yields first, taken to calculate the Hsu/Zhu ratio $\nu_{12}$.

2.3 Constitutive Laws of Materials

2.3.1 Uniaxial Constitutive Laws of Prestressed Steel Fiber Concrete

The constitutive model for PSFC along with the factors that will affect PSFC are summarized in this section. The results are plotted in Fig. 3. Note that the tensile stress is applied in 1-direction and the compressive stress in 2-direction. Development of these constitutive relationships has been reported by Hoffman (2010). These proposed constitutive laws of PSFC takes consideration on the effect of presence of the steel fibers in the concrete.

Fig. 3

Average stress–strain relationships of prestressed steel fiber concrete.

2.3.2 SFC in Tension

The relationships of $\sigma_{1}^{c}$ and the uniaxial strain $\overline{\varepsilon }_{1}$ of prestressed SFC are given as follows:

Stage UC:

$$ \sigma_{1}^{c} = E^{\prime}_{c} \bar{\varepsilon }_{1} + \sigma_{ci} ,\bar{\varepsilon }_{1} \le \left( {\bar{\varepsilon }_{cx} - \bar{\varepsilon }_{ci} } \right) $$

(13a)

Stage T1:

$$ \sigma_{1}^{c} = E^{\prime\prime}_{c} (\bar{\varepsilon }_{1} + \bar{\varepsilon }_{ci} ),\left( {\bar{\varepsilon }_{cx} - \bar{\varepsilon }_{ci} } \right) < \bar{\varepsilon }_{1} \le \left( {\varepsilon_{cy} - \bar{\varepsilon }_{ci} } \right) $$

(13b)

Stage T2:

$$ \sigma_{1}^{c} = E^{\prime\prime\prime}_{c} (\bar{\varepsilon }_{1} + \bar{\varepsilon }_{ci} ),\left( {\bar{\varepsilon }_{cy} - \bar{\varepsilon }_{ci} } \right) < \bar{\varepsilon }_{1} \le \left( {\varepsilon_{cult} - \bar{\varepsilon }_{ci} } \right) $$

(13c)

Stage T3:

$$ \sigma_{1}^{c} = E_{c}^{IV} (\bar{\varepsilon }_{1} + \bar{\varepsilon }_{ci} ),\bar{\varepsilon }_{1} > \left( {\varepsilon_{cult} - \bar{\varepsilon }_{ci} } \right) $$

(13d)

Where,

$E^{\prime}_{c}$ = decompression modulus of concrete given as $\frac{{2f^{\prime}_{c} }}{{\varepsilon_{0} }}$

$\sigma_{ci}$ = initial stress in SFC

$\bar{\varepsilon }_{ci}$ = initial strain in concrete due to prestress

$\bar{\varepsilon }_{cx}$ = extra concrete strain after decompression, taken as $\bar{\varepsilon }_{ci} - \frac{{\sigma_{ci} }}{{E^{\prime}_{c} }}$

$\varepsilon_{c\hbox{max} }$ = SFC maximum strain calculated by 0.04-$\varepsilon_{pi}$, where, $\varepsilon_{pi}$ = initial uniaxial strain of prestressing tendons

$\varepsilon_{cult}$ = SFC strain under ultimate stress, calculated by 0.01—$\varepsilon_{pi}$

$f_{cult}$ = SFC ultimate stress, taken as $(0.2FF + 12\rho_{l} )\sqrt {f^{\prime}_{c} }$, where, FF = fiber factor, $\rho_{l}$ = longitudinal steel ratio

$\varepsilon_{cy}$ = SFC yield strain taken as 0.0005

$f_{cy}$ = SFC effective yield stress, taken as $0.4 * FF * CF\sqrt {f^{\prime}_{c} }$, ($f^{\prime}_{c}$ and $\sqrt {f^{\prime}_{c} }$ are in MPa), CF = 1 for SFC tensile volume confined (sandwiched) by two or more tendons, or CF = ½ for SFC tensile volume unconfined by tendons

$E^{\prime\prime}_{c}$ = modulus of SFC, taken as $\frac{{f_{cy} }}{{\varepsilon_{cy} - \bar{\varepsilon }_{cx} }}$

$E^{\prime\prime\prime}_{c}$ = modulus of SFC, taken as $\frac{{f_{cult} - f_{cy} }}{{\varepsilon_{cult} - \varepsilon_{cy} }}$

$E_{c}^{IV}$ = modulus of SFC, taken as $\frac{{ - f_{cult} }}{{\varepsilon_{\hbox{max} } - \varepsilon_{cult} }}$

2.3.3 SFC in Compression

The average (smeared) constitutive laws of SFC compression stress $\sigma_{2}^{c}$ and the uniaxial compression strain $\bar{\varepsilon }_{2}$ are taken as follows:

$$ \sigma_{2}^{c} = \zeta f^{\prime}_{c} \left[ {2\left( {\frac{{\bar{\varepsilon }_{2} }}{{\zeta \varepsilon_{0} }}} \right) - \left( {\frac{{\bar{\varepsilon }_{2} }}{{\zeta \varepsilon_{0} }}} \right)^{2} } \right],\frac{{\bar{\varepsilon }_{2} }}{{\zeta \varepsilon_{0} }} \le 1, $$

(14a)

or

$$ \sigma_{2}^{c} = \zeta f^{\prime}_{c} \left[ {1 - \left( {\frac{{{{\bar{\varepsilon }_{2} } \mathord{\left/ {\vphantom {{\bar{\varepsilon }_{2} } {\zeta \varepsilon_{0} }}} \right. \kern-0pt} {\zeta \varepsilon_{0} }} - 1}}{{{4 \mathord{\left/ {\vphantom {4 \zeta }} \right. \kern-0pt} \zeta } - 1}}} \right)^{2} } \right],\frac{{\bar{\varepsilon }_{2} }}{{\zeta \varepsilon_{0} }} > 1 $$

(14b)

Where, $\zeta$ is the softening coefficient, which can be calculated as follows:

$$ \zeta = f\left( {f^{\prime}_{c} } \right)f\left( {\bar{\varepsilon }_{1} } \right)f\left( \beta \right)W_{p} Wf \le 0.9 , $$

(15)

Where,

$$ f\left( {f^{\prime}_{c} } \right) = \frac{5.8}{{\sqrt {f^{\prime}_{c} } }} \le 0.9 ( f^{\prime}_{c} \, in \, MPa), $$

(16)

$$ f\left( {\bar{\varepsilon }_{1} } \right) = \frac{1}{{\sqrt {1 + 400\bar{\varepsilon }_{1} } }} , $$

(17)

$$ f\left( \beta \right) = 1 - \frac{\left| \beta \right|}{{24^{ \circ } }},\beta = \frac{1}{2}\tan^{ - 1} \left[ {\frac{{\gamma_{21} }}{{\left( {\varepsilon_{2} - \varepsilon_{1} } \right)}}} \right], $$

(18)

$$ W_{p} = 1.15 + \frac{{\left| \beta \right|\left( {0.09\left| \beta \right| - 1} \right)}}{6} , $$

(19)

and

$$ Wf = 1 + 0.2FF $$

(20)

2.3.4 SFC in Shear

In the 1–2 coordinates, the relationship between the concrete stress ($\tau_{12}^{c}$) and the strain ($\gamma_{12}$) is reported by Zhu et al. (2001) and shown in Eq. (21).

$$ \tau_{12}^{c} = \frac{{\sigma_{1}^{c} - \sigma_{2}^{c} }}{{2(\varepsilon_{1} - \varepsilon_{2} )}}\gamma_{12} $$

(21)

where $\sigma_{1}^{c}$ and $\sigma_{2}^{c}$ are the average (smeared) concrete stresses; $\varepsilon_{1}$ and $\varepsilon_{2}$ are the biaxial smeared strains in the 1- and 2- directions of the principal applied stresses, respectively.

2.3.5 Prestressing Tendons Embedded in SFC

The prestressing tendons are embedded in SFC. The average (smeared) stress–strain relationship of PSFC is given as follows:

$$ f_{ps} = E_{ps} \bar{\varepsilon }^{\prime}_{s} \varepsilon_{s} < \frac{{0.7f_{pu} }}{{E_{ps} }}, $$

(22a)

or

$$ f_{ps} = \frac{{E^{\prime\prime}_{ps} \bar{\varepsilon }^{\prime}_{s} }}{{\left[ {1 + \left( {\frac{{E^{\prime\prime}_{ps} \bar{\varepsilon }^{\prime}_{s} }}{{f^{\prime}_{pu} }}} \right)^{5} } \right]^{{\frac{1}{5}}} }},\bar{\varepsilon }^{\prime}_{s} \ge \frac{{0.7f_{pu} }}{{E_{ps} }}, $$

(22b)

Where,

$E_{ps}$ = elastic modulus of prestressing strands, 200GPa

$\bar{\varepsilon }^{\prime}_{s}$ = $\bar{\varepsilon }_{s}$ + $\varepsilon_{dec}$, uniaxial steel bar strain

$f_{pu}$ = ultimate strength of prestressing strands, 1862 MPa

$E^{\prime\prime}_{ps}$ = modulus of prestressing strands in plastic area (Eq. (22)), 209 GPa

$f^{\prime}_{pu}$ = modified strength of prestressing strands, 1793 MPa

In the above equations, ps can be exchanged by $\ell p$ and $t{\text{p}}$ for the longitudinal tendons and the transverse tendons respectively (Fig. 4).

Fig. 4

Constitutive relationship of prestressing tendons.

2.3.6 Mild Steel Embedded in SFC

The mild steel bars are installed in concrete as those in SMM. The average (smeared) stress–strain relationships can be expressed as follows:

Stage 1:

$$ f_{s} = E_{s} \bar{\varepsilon }_{s} ,\bar{\varepsilon }_{s} \le \bar{\varepsilon }_{n} $$

(23)

Stage 2:

$$ f_{s} = f_{y} \times \left[ {(1 - 0.096FF)(0.91 - 2B) + (0.2FF + 1) \times (0.02 + 0.25B)\frac{{\bar{\varepsilon }_{s}^{\prime } }}{{\varepsilon _{y} }}} \right],\bar{\varepsilon }_{s} {\text{ > }}\bar{\varepsilon }_{n} $$

(24)

Stage 3 (unloading):

$$ f_{s} = f_{p} - E_{s} (\bar{\varepsilon }_{p} - \bar{\varepsilon }_{s} ),\bar{\varepsilon }_{s} < \bar{\varepsilon }_{p} $$

(25)

Where,

$$ \bar{\varepsilon }_{n} = \varepsilon_{y} (0.93 - 2B) $$

(26a)

$$ B = \frac{1}{\rho }\left( {\frac{{f_{cr} }}{{f_{y} }}} \right)^{1.5} $$

(26b)

$\varepsilon_{cr}$ = 0.00008, concrete cracking strain

$f_{cr}$ = $0.31\sqrt {f^{\prime}_{c} }$ ($f^{\prime}_{c}$ and $\sqrt {f^{\prime}_{c} }$ are in MPa), concrete cracking stress (Fig. 5)

Fig. 5

Stress-strain relationship of reinforcing steel using two-straight line expression.

2.4 Experimental Verification

The SMM-PSFC was used to realize the experimental shear behavior of PSFC membrane elements with different steel grid orientations and steel percentages (Laskar et al. 2014). Figure 6 shows the validity of SMM-PSFC in predicting the behavior of PSFC panels under pure shear. The figure shows the comparison between the analytical and the measured shear stress–strain curves of a PSFC panel by Hoffman (2010) with results predicted by SMM-PSFC. It can be seen that the predictions from SMM-PSFC are in good agreement.

Fig. 6

Predicted versus experimental shear stress–strain curves of a typical PSFC panel (Hoffman 2010).

3 Simulation of PSFC Beams

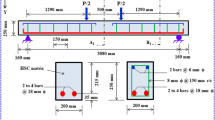
The PSFC beams shown in Fig. 7 have been analysed using SCS. Details and shear behavioral characteristics of the beams are given in Tadepalli et al. (2014, 2015). Some tests of PSFC beams were carried out to validate the SCS program, which was developed using the constitutive laws of PSFC in SMM-PSFC (Hoffman 2010). Since the PSFC beams were tested under monotonic loads, this validation and applicability of SCS program is only suitable in predicting the behaviour of PSFC structures under monotonic loading.

Fig. 7

Cross sections of I-beam and box-beam.

3.1 Analytical Model

Two types of elements were chosen to analyze the PSFC beams. The prestressing loads exerting on the beam were treated as external forces. These loads are the total prestressing forces after losses. The top and bottom flanges of the PSFC beams were represented by NonlinearBeamColumn elements and the web of the beams were modeled as PCPlaneStress quadrilateral elements.

All the concentrated loads applied on the beam in the model acted at nodes. The effect of bearing plates, which were actually used in the load-test to apply vertical loads on the beam, was ignored for simplicity. The loads were distributed among three nodes adjacent to the location of the applied load. The analysis yielded similar results in the cases when (a) larger load was applied at the node corresponding to the actual loading point and lower loads were applied at the two adjacent nodes and (b) loads were distributed equally among the three nodes. Hence, the concentrated vertical loads on the beams were modeled at a node corresponding to the actual loading point and two adjacent nodes. The results of beam analysis i.e. vertical forces and nodal deflections, were computed at every loading step that had numerically converged. Additionally, the stresses and strains in the beam elements were also calculated by the program (Laskar 2009).

3.2 SCS FEM Models of PSFC Beams

3.2.1 I-Beams

The PSFC I-beams was meshed using the SCS program, as represented in Figs. 8 and 9. Sixteen and fifteen NonlinearBeamColumn elements were used to simulate the bottom and top flanges in the case of web-shear and flexure-shear failure modes, respectively. The method of the cross section discretization of the two flanges is that forty equivalent rectangular NonlinearBeamColumn elements are meshed to model each flange, as shown in Fig. 10. Two of the twelve tendons in the specimens were provided in the NonlinearBeamColumn elements representing the bottom flange of the specimens. The remaining tendons were provided in the quadrilateral elements used to represent the webs of these specimens.The tendons have initial strains, it was taken into account by using the TendonL01 material module. The steel and concrete fibers were defined by using Steel02 and Concrete01 constitutive modules, respectively.

Fig. 8

FEM model of PSFC I-beams tested under web-shear.

Fig. 9

FEM model of PSFC I-beams tested under flexural-shear.

Fig. 10

Cross-section discretization for PSFC I-beams governed by web-shear.

The Concrete01 module used herein was a uniaxial material module of concrete previously created in OpenSees following the modified Kent and Park model (Park et al. 1982). The steel02 module used in the SCS was a uniaxial Menegotto-Pinto object (Dhakal and Maekawa 2002). This material object also allowed user to enter the initial strain in the steel, which is useful in modeling the prestressing strands.

The web of the beams have been divided into sixteen and fifteen PCPlaneStress quadrilateral elements in case of web shear and flexural shear, respectively. The steel ratio in the vertical direction was taken as a very small number to avoid numerical problems during the analysis.

3.2.2 Box-Beams

The PSFC Box-beams was meshed using the SCS program, as shown in Figs. 11, 12 and 13. The two flanges in the beams were defined as 18 NonlinearBeamColumn elements each. The method of the cross section discretization of the two flanges is that forty equivalent rectangular NonlinearBeamColumn elements are meshed to model each flange, as shown in Fig. 14. The web of the beam has been divided into eighteen PCPlaneStress quadrilateral elements. The steel ratio in the vertical direction was taken as a very small number to avoid numerical problems in analysis. The tendons and concrete were defined by using TendonL01 and ConcreteR01 constitutive modules in the PCPlaneStress elements, respectively.

Fig. 11

FEM model of PSFC box-beams tested under web-shear (a/d = 1.8).

Fig. 12

FEM model of box-beams tested under web-shear (a/d = 2.5).

Fig. 13

FEM model of box-beams tested under flexure-shear (a/d = 4.1).

Fig. 14

Cross-section discretization for PSFC box-beams governed by web-shear.

3.3 Comparison of Experimental and Analytical Results

3.3.1 Web-Shear Failure

The analytical and tested load–displacement curves for all PSFC I-beams in web-shear failure mode are shown in Figs. 15 to 18. These figures show that the results obtained from the numerical analysis correspond well with results obtained from the test. The general trend observed in the beam (R1 to R4) tests, i.e. increase in load carrying capacity of beams with increase in fiber-factor (FF), was accurately predicted by the analysis program.

Fig. 15

Comparison of analytical and experimental results of beam R1.

Fig. 16

Comparison of analytical and experimental results of beam R2.

Fig. 17

Comparison of analytical and experimental results of beam R3.

Fig. 18

Comparison of analytical and experimental results of beam R4.

Unlike Beams R1, R2 and R3 the prediction of the post-cracking stiffness of Beam R4 did not match well with the experimental results. This is due to the fact that while testing Beam R4, the data acquisition system (DAS) got some problem in the electronic part and recorded invalid values and stopped after some time. After resolving the problem with DAS, the test has been restarted. This invalid data is the reason for the lower cracking value and post cracking stiffness observed during the testing of the beam than those obtained from the analysis.

All the box-beams encountered a local flexural failure at top flange and end block-out of the beams, which prevented the accomplishment of expected ultimate shear failure and anticipated ductility levels (Tadepalli et al. 2014). This can be clearly observed from all the curves shown in Figs. 19 to 22. The analysis was able to satisfactorily predict the ultimate load capacity and ductility of the box-beams tested.

Fig. 19

Comparison of analytical and experimental results of beam RB1.

Fig. 20

Comparison of analytical and experimental results of beam RB2.

Fig. 21

Comparison of analytical and experimental results of beam RB4.

Fig. 22

Comparison of analytical and experimental results of beam RB6.

3.3.2 Flexure-Shear Failure

The measured and calculated load-deformation curves for all beams with flexure-shear failure are shown in Figs. 23 to 26. Figures 23 and 24 indicate the results from I-beams, while Figs. 25 and 26 show those for box-beams. These figures show that the results obtained from the numerical analysis correspond well with results obtained from the test. The analysis could well predict the lower load carrying capacity of beams tested under flexural shear in comparison to the beams tested under web shear failure having same amount of steel fibers. The higher ductility observed in the behavior of beams under flexural-shear failure, than all the web shear specimens was also well predicted in the analysis.

Fig. 23

Comparison of analytical and experimental results of beam R5.

Fig. 24

Comparison of analytical and experimental results of beam R6.

Fig. 25

Comparison of analytical and experimental results of beam RB3.

Fig. 26

Comparison of analytical and experimental results of beam RB5.

All the box-beams had a local failure, which prevented them to reach up to their ultimate shear capacity and also the ductility. This can be clearly observed from all the curves shown in Figs. 25 and 26. The analysis was able to predict the true ultimate load capacity and ductility.

4 Conclusion

Using the constitutive laws of PSFC established previously, an analytical model was developed and implemented in a FEM program framework (OpenSees) to simulate the shear behavior of the PSFC beams. Using this computer program, the load–deflection curves of all the I- and box-beams are simulated with acceptable accuracy.