Abstract
This paper presents a revised procedure for computation of double-K fracture parameters of concrete split-tension cube specimen using weight function of the centrally cracked plate of finite strip with a finite width. This is an improvement over the previous work of the authors in which the determination of double-K fracture parameters of concrete for split-tension cube test using weight function of the centrally cracked plate of infinite strip with a finite width was presented. In a recent research, it was pointed out that there are great differences between a finite strip and an infinite strip regarding their weight function and the solution of infinite strip can be utilized in the split-tension specimens when the notch size is very small. In the present work, improved version of LEFM formulas for stress intensity factor, crack mouth opening displacement and crack opening displacement profile presented in the recent research work are incorporated. The results of the double-K fracture parameters obtained using revised procedure and the previous work of the authors is compared. The double-K fracture parameters of split-tension cube specimen are also compared with those obtained for standard three point bend test specimen. The input data required for determining double-K fracture parameters for both the specimen geometries for laboratory size specimens are obtained using well known version of the Fictitious Crack Model.
Similar content being viewed by others
1 Introduction
It is well known that fracture parameters of quasibrittle material like concrete cannot be determined by directly applying the concepts of linear elastic fracture mechanics (LEFM) because of the existence of large and variable size of fracture process zone (FPZ) ahead of a crack-tip. In order to account for and characterize FPZ in the analysis, several non-linear fracture mechanics models have been developed which primarily involve cohesive crack model (CCM) or fictitious crack model (FCM) (Hillerborg et al. 1976; Modeer 1979; Petersson 1981; Carpinteri 1989; Planas and Elices 1991; Zi and Bažant 2003; Roesler et al. 2007; Park et al. 2008; Zhao et al. 2008; Kwon et al. 2008, Cusatis and Schauffert 2009, Elices et al. 2009; Kumar and Barai 2008b, 2009b) and crack band model (CBM) (Bažant and Oh 1983), two parameter fracture model (TPFM) (Jenq and Shah 1985), size effect model (SEM) (Bažant et al. 1986), effective crack model (ECM) (Nallathambi and Karihaloo 1986), KR-curve method based on cohesive force distribution (Xu and Reinhardt 1998, 1999a), double-K fracture model (DKFM) (Xu and Reinhardt 1999a, b, c) and double-G fracture model (DGFM) (Xu and Zhang 2008).
In recent time, much of research and studies (Xu and Reinhardt 1999a, b, c, 2000; Zhao and Xu 2002; Zhang et al. 2007; Xu and Zhu 2009; Kumar and Barai 2008a, 2009a, 2010; Kumar 2010; Zhang and Xu 2011; Kumar and Pandey 2012; Hu and Lu 2012; Murthy et al. 2012; Hu et al. 2012; Ince 2012; Kumar et al. 2013; Choubey et al. 2014; Kumar et al. 2014) have been carried out to determine and characterize the fracture parameters of concrete using double-K fracture model for which the reasons are obvious (Kumar et al. 2013). The double-K fracture model is characterized by two material parameters: initial cracking toughness K ini IC and unstable fracture toughness K un IC . The initiation toughness is defined as the inherent toughness of the materials, which holds for loading at crack initiation when material behaves elastically and micro cracking is concentrated to a small-scale in the absence of main crack growth. It is directly calculated by knowing the initial cracking load and initial notch length using LEFM formula. The total toughness at the critical condition is known as unstable toughness K un IC which is regarded as one of the material fracture parameters at the onset of the unstable crack propagation and it can be obtained by knowing peak load and corresponding effective crack length using the same LEFM formula. Recently, Kumar and Pandey (2012) presented the formulation and determination of double-K fracture parameters using split-tension cube test specimen using weight function method in which the LEFM formulas for stress intensity factor (SIF), crack mouth opening displacement (CMOD) and crack opening displacement (COD) profile derived by Ince (2010) and the universal weight function of Wu et al. (2003) were adopted. The authors (Kumar and Pandey 2012) mentioned that there are several advantages of using split-tension cube (STC) test specimen over the testing of other specimens like three point bend test (TPBT), compact tension (CT) and wedge splitting test (WST) specimens. However, there should be a limitation that the notch can be only produced at the time of casting of concrete cubes (pre-cast notch) in the split tension cube specimen. The authors also presented the results of the initial cracking toughness, cohesive toughness and unstable fracture toughness obtained using split tension cube test specimen and they were compared with those obtained using standard compact tension specimen. From the study it was concluded that the double-K fracture parameters as obtained using split-tension cube test are in good agreement and consistent with those as calculated using standard compact tension specimen. However, the results of fracture parameters are influenced by the distributed-load width during the loading of split-tension cube specimen and it was observed that the values of unstable fracture toughness and cohesive toughness increase with increase in the distributed-load width whereas the initial cracking toughness is not significantly affected by the distributed-load width. In the formulation, the authors (Kumar and Pandey 2012) used the weight function of the centrally cracked infinite strip with a finite width specimen (Tada et al. 2000) and the equivalent four terms of universal weight function (Wu et al. 2003) for computing the value of cohesive toughness and consequently determining the initial cracking toughness. Later, Ince (2012) put forward a method for determination of double-K fracture parameters using weight function for split—tension specimens such as splitting tests on cubical, cylindrical and diagonal cubic concrete samples. The author pointed out that there are great differences between a finite strip and an infinite strip regarding their weight function and the solution of infinite strip can be utilized in the split-tension specimens when the notch size is very small. It was concluded that the central cracked plate can be considered as an infinite strip when the length/width (l/D) ratio of a plate is equal or greater than 3 (Isida 1971, Tada et al. 2000). In case of a cube-split tension test specimen the value of the length/characteristic dimension (l/D) ratio is taken to be 1 for which Ince (2012) derived the four term universal weight function using boundary element method and finite element method. The author also presented the improved version of LEFM formulas for stress intensity factor, CMOD and COD profile over the previously derived LEFM equations by the same author (Ince 2010) for split tension cube test specimen. In view of the above development, it was felt necessary to carry out a comparative study on the double-K fracture parameters computed using the procedure outlined by Kumar and Pandey (2012) and using the weight function of the centrally cracked plate of finite strip with a finite width incorporating the improved version of LEFM formulas for stress intensity factor, CMOD and COD profile derived by Ince (2012).
The paper presents the revised procedure for determination of double-K fracture model using weight function method for the split-tension cube specimen of concrete considering improved LEFM formulas for stress intensity factor, CMOD and COD profile and the weight function of the centrally cracked plate of finite strip with a finite width derived by Ince (2012). The results of the fracture parameters obtained using revised procedure and the previous work of Kumar and Pandey (2012) are compared. Further, the double-K fracture parameters of split-tension cube specimen are also compared with those obtained for standard three point bend test specimen. The input data required for determining for split-tension cube test and three point bend test for laboratory size specimens are obtained using well known version of the fictitious crack model.
2 Dimensions of Test Specimens
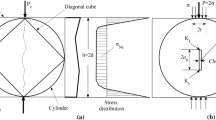
For present investigation, the standard test geometries, dimensions and loading conditions for STC and TPBT specimens are considered as shown in Fig. 1. The symbols in Fig. 1(a): a o , D, h and t are half of the initial notch-length, characteristic dimension as specimen size (D = h/2), height or total depth and half of the width of distributed load respectively for STC geometry. RILEM Technical Committee 50-FMC (1985) has recommended the guidelines for determination of fracture energy of cementitous materials using standard three-point bend test on notched beam. This method has been widely used for determination of fracture energy of concrete with certain modification in the experimental setup (Lee and Lopez 2014). In present study, standard three—point bend test (RILEM Technical Committee 50-FMC 1985) is considered for which the symbols: B, D and S in Fig. 1b are the width, depth and span respectively with S/D = 4.
3 Determination of Double-K Fracture Parameters for STC Specimen
3.1 Assumptions
Linear asymptotic superposition assumption is considered to introduce LEFM for calculating the double-K fracture parameters. The hypotheses of the assumption are given below:
-
1.
the nonlinear characteristic of the load-crack mouth opening displacement (P-CMOD) curve is caused by fictitious crack extension in front of a stress-free crack; and
-
2.
an effective crack consists of an equivalent-elastic stress-free crack and equivalent-elastic fictitious crack extension.
A detailed explanation of the hypotheses may be seen elsewhere (Xu and Reinhardt 1999b).
3.2 Effective Crack Extension
For the applied load (Fig. 1) on the STC specimen, the critical value of CMOD (CMODc) is measured across the crack faces at the centre of specimen. The P-CMOD curve up to peak load for this test geometry should be known a priori for determining the value of effective crack extension during the crack propagation. Using linear asymptotic superposition assumption, the equivalent-elastic crack length a c corresponding to maximum load P u is solved using the revised LEFM formulae (Ince 2012). Hence, the CMOD is expressed as:
In which α = a/D, β is the relative load-distributed width and expressed as β = 2t/h = t/D, V(α,β) is dimensionless geometric function, coefficients B i (i = 0 to 5) are the function of β as given in Table 1. Equation (2) is valid for 0.1 ≤ α ≤ 0.9 within 0.3 % accuracy for 0 ≤ β ≤ 0.2. The modulus of elasticity of concrete (E) obtained using cylinder test is taken as a constant value for a particular concrete mix. Ince (2012) used boundary element numerical method to improve the LEFM formulas over the previous LEFM formulas (Ince 2010) for the split tension cube specimens which was based on centrally cracked infinite strip with a finite width specimen. Equation (2) and Table 1 used in the present study are extracted by Ince (2012) from the numerical results based on centrally cracked finite strip with a finite width specimen. Since the values of coefficients B i (Table 1) are given (Ince 2012) at discrete intervals, these coefficients can be determined by linear interpolation at any value of β for the given range 0 ≤ β ≤ 0.2.
Also, the nominal stress for STC test specimen in Eq. (1) can be written using the following formula (Timoshenko and Goodier 1970).
At critical condition that is at maximum load P u the half of crack length a becomes equal to a c and σ N to σ Nu in which σ Nu is the maximum nominal stress. Karihaloo and Nallathambi (1991) concluded that almost the same value of E might be obtained from P-CMOD curve, load–deflection curve and compressive cylinder test. Hence, in case that is not known the value of E determined using compressive cylinder tests may be used to obtain the critical crack length of the specimen.
3.3 Calculation of Double-K Fracture Parameters
A linearly varying cohesive stress distribution is assumed in the fictitious crack zone, which gives rise to cohesion toughness as a part of total toughness of the cracked body. Superposition method is used in order to calculate the stress intensity factor (SIF) at the tip of effective crack length K I . According to this method, total stress intensity factor K I is taken as the summation of stress intensity factor caused due to external load K P I and stress intensity factor contributed by cohesive stress K C− I as shown in Fig. 2. The value of K I is expressed in the following expression:
After determining the critical effective crack extension at unstable condition of loading, the unstable fracture toughness K un IC is determined using the revised LEFM formulae (Ince 2012) for which the stress intensity factor is expressed as:
where k(α, β) is a geometric factor and coefficients A i (i = 0–5) are the function of β as summarized in Table 1. Equation (6) yields results within 0.7 % accuracy for 0.1 ≤ α ≤ 0.9 and 0 ≤ β ≤ 0.2. Within the range of 0 ≤ β ≤ 0.2, any value of coefficients A i can be determined by linear interpolation. The unstable fracture toughness K un IC is calculated using Eq. (5) at maximum load P u when a becomes equal to a c and σ N to σ Nu .
If the crack initiation load P ini is known from experiment, the initiation toughness K ini IC is calculated using Eq. (5) in which P is equal to P ini and a is equal to a o . Alternatively, it can be determined analytically by applying the following relation.
Equation (7) is known as inverse method for determining the initiation toughness.
4 Determination of SIF Due to Cohesive Stress
4.1 Cohesive Stress Distribution
The cohesive stress acting in the fracture process zone on STC test specimen is idealized as series of pair normal forces subjected symmetrically to central cracked specimen of finite strip and a finite width as shown in Fig. 3. The linearly varying distribution of cohesive stress is also shown in Fig. 4.
A centrally cracked specimen with finite strip of a finite width plate subjected to pair of normal forces as shown in Fig. 3 takes into consideration for a split tension test cube specimen where the value of the length/characteristic dimension (l/D) ratio becomes 1. The SIF due to cohesive stress distribution as shown in Fig. 4 becomes to cohesive toughness K C IC of the material at the critical loading condition with negative value because of closing stress in fictitious fracture zone. However, the absolute value of K C IC is taken as a contribution of the total fracture toughness (Xu and Reinhardt 1999b) at the critical condition.
At this loading condition, the crack-tip opening displacement (CTOD) is termed as critical crack-tip opening displacement (CTODc). In Fig. 4, the σ s (CTODc) is cohesive stress at the tip of initial notch where CTOD is equal to CTODc and then σ(x) can be expressed as:
The value of σ s (CTODc) is calculated using softening functions of concrete. In the present work, the nonlinear softening function (Reinhardt et al. 1986) is used for the computation which can be expressed as:
The value of total fracture energy of concrete G F is expressed as:
In which, σ(w) is the cohesive stress at crack opening displacement w at the crack-tip and c 1 and c 2 are the material constants. Also, w = w c for f t = 0, i.e., w c is the maximum crack opening displacement at the crack-tip at which the cohesive stress becomes to be zero. The value of w c is computed using Eq. (10) for a given set of values c1, c2 and G F . For normal concrete the value of c1 and c2 is taken as 3 and 7, respectively.
4.2 Determination of CTODc
For a given value of critical crack mouth opening displacement CMODc, the crack opening displacement within the crack length COD(x) is computed using the revised expression (Ince 2012) as given below.
The accuracy of Eq. (11) is greater than 4 % for 0.1 ≤ α ≤ 0.9 and any value of β and is greater than 2.5 % for 0.1 ≤ α ≤ 0.6 and any value of β. The value of x is taken as a o and a as a c for evaluation of CTODc using Eq. (11).
4.3 Calculation of Cohesive Toughness Using Weight Function Approach
According to weight function approach (Bueckner 1970, Rice 1972), the SIF for mode –I loading is given by following expression.
where σ(x) is the distribution of stress along the crack line x in the uncracked body, the term m(x,a) is known as weight function, a is the crack length and dx is the infinitesimal length along the crack surface. The four term universal form of weight function (Glinka and Shen 1991, Kumar and Barai 2008a, 2009a, 2010) is written as:
For centrally through cracked specimen of infinite strip and a finite width subjected to pairs of normal forces symmetrically (Fig. 3), the weight function as given by Tada et al. (2000) is expressed as:
Equation (14) as equivalently expressed in terms of universal weight function m(x,a) of Eq. (13) by Wu et al. (2003) was used by Kumar and Pandey (2012) in the previous formulation. In the present investigation the weight function parameters M 1, M 2 and M 3 derived by Ince (2012) for the split tension cube specimen are used. According to Ince (2012) the parameters of four term weight function for a centrally through cracked specimen of finite strip and a finite width subjected to pairs of normal forces (Fig. 3) can be obtained as:
where α = a/D and m ij (i = 1–3 and j = 0–7) are the coefficients of the polynomial Eq. (15) as presented in Table 2. The sixth degree polynomial (m i7 = 0) is used for M 2. Equation (15) is valid for 0 ≤ a/D ≤ 0.9 and 0 ≤ x/a 1 (exactly 0.993). The accuracy of Eqs. (13) and (15) is greater than 3 % for all the split—tension cube specimens.
Once the weight function parameters are determined, Eq. (12) is used to calculate the SIF at critical condition (cohesive toughness) due to trapezoidal cohesive stress distribution as shown in Fig. 4. The value of σ(x) in Eq. (12) is replaced by Eq. (8), hence the closed form expression of K C IC can be obtained in the following form.
where, \( A_{1} = \sigma_{s} (CTOD_{c} ),A_{2} = \frac{{f_{t} - \sigma_{s} (CTOD_{c} )}}{{a - a_{o} }} \) and \( s = (1 - a_{o} /a) \), also a = a c at P = P u . After computing the value of K C IC using Eq. (16), initiation toughness can be evaluated using Eq. (7).
5 Fictitious Crack Model and Material Properties for Double-K Fracture Model
The cohesive crack model (Modeer 1979; Petersson 1981; Carpinteri 1989; Planas and Elices 1991; Zi and Bažant 2003; Roesler et al. 2007, Park et al. 2008, Zhao et al. 2008, Kwon et al. 2008; Cusatis and Schauffert 2009; Elices et al. 2009; Kumar and Barai 2008b, b) is developed for STC and TPBT specimens to determine the input data such as P u and CMODc for these specimens. Three material properties such as modulus of elasticity E, uniaxial tensile strength f t , and fracture energy G F are required to model FCM. In this method, the governing equation of COD along the potential fracture line is written. The influence coefficients of the COD equation are determined using linear elastic finite element method. Four noded isoparametric plane elements are used in finite element calculation. The COD vector is partitioned according to the enhanced algorithm introduced by Planas and Elices (1991). Finally, the system of nonlinear simultaneous equation is developed and solved using Newton–Raphson method. For standard STC and TPBT specimens with B = 100 mm having size range D = 200-500 mm, the finite element analysis is carried out for which the one-quarter of STC and half of TPBT specimens are discretized due to symmetry as shown in Fig. 5 considering 80 numbers of equal isoparametric plane elements along the characteristic dimension D. In the discretization, both the specimens are divided into three bands perpendicular to characteristic dimension D such as D/4, D/4 and D/2 in case of STC specimen and 0.25D, 0.75D and D in case of TPBT specimen as shown in Fig. 5. This arrangement facilitates to obtain finer mesh size near the potential fracture line. For STC specimen, the number of divisions is taken as 20, 5 and 5 in the bands D/4, D/4 and D/2 respectively whereas it is 20, 10 and 5 in the bands 0.25D, 0.75D and D respectively for TPBT specimen. Ten nodes from top along the potential fracture line are restrained against horizontal movement and all the nodes at the bottom perpendicular to fracture line are restrained against vertical movement in case of STC specimen. For the TPBT specimen, three nodes from top along the potential fracture line are restrained in horizontal direction. The concrete mix with material properties: ν = 0.18, f t = 3.21 MPa, E = 30 GPa, and G F = 103 N/m along with nonlinear stress-displacement softening relation with c1 = 3 and c 2 = 7 are used as the input parameters of FCM.
From simulation of FCM, the results of peak load P u versus CMODc for TPBT specimen at a constant a o /D ratio of 0.3 are presented in Table 3. Similar results of peak load P u and the corresponding CMODc at different load distributed widths (β = 0.0, 0.05, 0.1 and 0.15) for STC specimens of varying sizes (200–500 mm) at a constant a o /D ratio of 0.3 are also presented in Table 3.
6 Results and Discussion
The input parameters such as P u , CMODc, E and softening function of concrete are required from the tests for determining double-K fracture parameters of concrete using weight function analytical method. In the present study, the values of E, f t , nonlinear softening function (Eq. (9)) as mentioned in Sect. 5 and the values of Pu-CMODc for STC and TPBT specimens obtained from FCM are used to determine double-K fracture parameters. The weight function method with four terms is applied to calculate double-K fracture parameters in which the value of critical crack extension a c is obtained using improved Eq. (1) for STC specimen. For given values of a c and CMODc, the values of CTODc are determined using revised Eq. (11). The values of a c and CTODc are also determined using corresponding equations presented in the previous work of Kumar and Pandey (2012) which were based on LEFM equations given by Ince (2010). The values of a c and CTODc for TPBT specimen are determined as mentioned elsewhere (Kumar and Barai 2008a, 2010). All the values of a c and CTODc determined as above are plotted in Figs. 6 and 7, respectively. For determining the value of K C IC using weight function method, first of all the four parameters M 1, M 2 and M 3 of four terms weight function are computed using Eq. (15) and Table 2, then closed form expression (Eq. (16)) is used to obtain the value of K C IC and finally the K ini IC is determined using inverse procedure (Eq. (7)). For TPBT specimen, double-K fracture parameters are determined in a similar manner using four terms weight function method as mentioned elsewhere (Kumar and Barai 2008a, 2010). Thus the values of K un IC , K C IC and K ini IC as obtained for STC for different distributed-load widths (0 ≤ β ≤ 0.15) and TPBT specimens for specimen size 200 ≤ D ≤ 500 mm at a o /D ratio of 0.3 are plotted in Figs. 8, 9 and 10 respectively. The legends in Figs. 6, 7, 8, 9 and 10 marked with star (*) indicate the fracture parameters of the specimens determined using revised equations presented in this work whereas those legends with no mark with star (*) show the respective parameters of the specimens determined using the equations presented by Kumar and Pandey (2012).
Comparison in the values of ac/D for STC obtained using the previous method (Kumar and Pandey 2012) and the present revised method.
Comparison in the values of CTODc for STC obtained using the previous method (Kumar and Pandey 2012) and the present revised method.
Comparison of unstable fracture toughness for STC obtained using the previous method (Kumar and Pandey 2012) and the present revised method.
Comparison of cohesive toughness for STC obtained using the previous method (Kumar and Pandey 2012) and the present revised method.
Comparison of initial cracking toughness for STC obtained using (Kumar and Pandey 2012) and the present revised method.
From Figs. 6 and 7 it can be seen that the revised formulae and the previous LEFM equations (Kumar and Pandey 2012) yield the same results of critical values of effective crack length and crack tip opening displacement. These values for split tension cube specimen and three point bend test specimen also depend upon the size of the specimens and show similar pattern. The value a c /D decreases with the increase in specimen size whereas CTODc increases with the increase in specimen size. From Fig. 6 it can be seen that for STC specimen these parameters also depend on distributed-load width and the a c /D ratio shows maximum deviation for STC specimen with β = 0.15 from those obtained for TPBT for a given specimen size. This deviation is more for the lower specimen size and seems to be converging at higher specimen size. The a c /D values for STC specimen are on higher side as compared with those of TPBT specimen for all values of distributed-load width (0 ≤ β ≤ 0.15) considered in the study. On an average, these values for STC for all values of β (0 ≤ β ≤ 0.15) are more than those for TPBT specimen by approximately 4.6 % and 0.43 % for D = 200 mm and D = 500 mm, respectively.
From Fig. 7 it can be observed that for STC specimen the value of CTODc depends on distributed-load width and the value of CTODc shows maximum deviation for STC specimen having β = 0 from those obtained for TPBT for a given specimen size. The CTODc values for STC specimen are in lower side as compared with those of TPBT specimen for all values of distributed-load width (0 ≤ β ≤ 0.15). On an average, these values for STC for all values of β (0 ≤ β ≤ 0.15) are less than those for TPBT specimen by approximately 19.9 and 18.3 % for D = 200 mm and D = 500 mm respectively.
It can be observed from Fig. 8 that the values of K un IC determined using LEFM equations presented elsewhere (Kumar and Pandey 2012) and the revised LEFM equations in this work are the almost same for specimen sizes (D = 200–500 mm) for all values of β (0 ≤ β ≤ 0.15). It is also seen from the figure that the unstable fracture toughness obtained from STC specimen is compatible with that of TPBT specimen. The value of K un IC for STC is the lowest for distributed-load width β = 0 and is the highest for β = 0.15 which is in close agreement with that obtained from TPBT specimen for all sizes of specimens. The values of K un IC are 36.70 and 39.91 MPa mm1/2 for STC with β = 0.15 and 38.16 and 42.10 MPa mm1/2 for TPBT specimens for specimen size 200 mm and 500 mm respectively. It seems from Fig. 8 that there is relatively more difference in results of unstable fracture toughness between STC with β = 0 and TPBT. Therefore, in case STC specimen is adopted to replace TPBT to test unstable fracture toughness of concrete, the STC with β = 0.15 can be considered to be reasonable. That means the unstable fracture toughness of concrete can be determined using STC specimen.
The value of cohesive toughness obtained using equations presented elsewhere (Kumar and Pandey 2012) and the revised procedure in this work, varies with the value of β for STC specimen. The values of cohesive toughness for STC and TPBT specimens shown in Fig. 9 also show that these values either obtained using STC specimen or TPBT specimen are in consistent with each other.
The effect of finite strip in the present revised work over the infinite strip (previous work of Kumar and Pandey (2012)) of finite width cracked specimen on the cohesive toughness values for the 0 ≤ β ≤ 0.15 is clearly observed from Fig. 9. It can be seen that for all values of distributed load width, the values of K C IC obtained considering the finite strip plate are slightly on higher side than those obtained considering the infinite strip plate.
For STC specimen with infinite strip and β = 0, the values of K C IC are found to be 29.36 MPa mm1/2 and 23.87 MPa mm1/2 for D = 500 mm and 200 mm respectively whereas those values are obtained as 29.96 MPa mm1/2 and 24.55 MPa mm1/2 for finite strip for D = 500 mm and 200 mm respectively. Similarly, for STC specimen with infinite strip and β = 0.15, the value of K C IC are found to be 30.64 MPa mm1/2 and 26.93 MPa mm1/2 for D = 500 mm and 200 mm respectively whereas those values are obtained as 31.34 MPa mm1/2 and 27.98 MPa mm1/2 for finite strip for D = 500 mm and 200 mm respectively. On an average for all values of β, the K C IC as obtained using finite strip is 2.14 and 3.29 % more than those obtained using infinite strip of plate for D = 500 mm and 200 mm respectively. Also, the values of K C IC as determined using finite strip of STC is 4.82 and 1.86 % less than those obtained using three point bend test specimen for D = 500 mm and 200 mm respectively. It is also observed from Fig. 9 that the size effect on the K C IC values for STC specimen is less significant than that presented for three point bend test.
It can be observed from Fig. 10 that for STC specimen with infinite strip and β = 0, the values of K ini IC are found to be 9.46 MPa mm1/2 and 8.32 MPa mm1/2 for D = 500 mm and 200 mm respectively whereas those values are obtained as 8.83 MPa mm1/2 and 8.68 MPa mm1/2 for finite strip for D = 500 mm and 200 mm respectively. Similarly, for STC specimen with infinite strip and β = 0.15, the values of K ini IC are found to be 9.26 MPa mm1/2 and 9.78 MPa mm1/2 for D = 500 mm and 200 mm respectively whereas those values are obtained as 8.71 MPa mm1/2 and 8.74 MPa mm1/2 for finite strip for D = 500 mm and 200 mm respectively. On an average for all values of β, the K ini IC obtained using finite strip is 6.21 and 5.96 % lower than those obtained using infinite strip of plate for D = 500 mm and 200 mm respectively. Also, the values of K ini IC as determined using finite strip of STC is 11.70 and 26.10 % less than those obtained using three point bend test specimen for D = 500 mm and 200 mm, respectively. According to the present trend, it seems that the difference in the value of K ini IC obtained between the STC and TPBT specimens may further increase for smaller size specimens such as 150 mm or 100 mm. As per the common convention, this difference should not be more than ±25 % in the fracture test which is a matter of further investigation. It is also seen from Fig. 10 that the size effect on the K ini IC values for STC specimen is less significant than that presented for three point bend test.
7 Conclusions
A revised formulation for determination of double-K fracture parameters using weight function method for split-tension cube test is presented in the paper. In the revised procedure, the weight function of the centrally cracked plate of finite strip with a finite width is used which is an improvement over the previous work of the authors. From the present study considering the specimen sizes (D = 200–500 mm) and distributed-load width (0 ≤ β ≤ 0.15) of split-tension cube test the following conclusions can be drawn.
-
Use of weight function for split-tension cube test considering a centrally cracked plate of finite width with the finite strip or the infinite strip yields the same results of critical values of effective crack length, critical value of crack tip opening displacement and unstable fracture toughness of concrete.
-
For all values of distributed load width (0 ≤ β ≤ 0.15), the values of cohesive toughness obtained considering the finite strip plate is slightly higher than those obtained considering the infinite strip plate. On an average cohesive toughness obtained using finite strip is 2.14 % and 3.29 % more than those obtained using infinite strip of plate for D = 500 mm and 200 mm, respectively
-
Consequently, on an average for all values distributed load width (0 ≤ β ≤ 0.15), the initial cracking toughness determined using finite strip is 6.21 and 5.96 % lower than those obtained using infinite strip of finite width plate for D = 500 mm and 200 mm respectively.
-
The value of unstable fracture toughness determined using finite strip of split-tension cube specimen is the lowest for distributed-load width β = 0 and is the highest for β = 0.15 which is in close agreement with that obtained from three point bed test for all sizes of specimens. Also, on an average for all values of the distributed-load width, the values of cohesive toughness determined using finite strip of split-tension cube specimen is 4.82 and 1.86 % less than those obtained using three point bend test specimen for D = 500 mm and 200 mm respectively. Further, on an average for all values of distributed-load width, the values of initial cracking toughness determined using finite strip of split-tension cube specimen is 11.70 and 26.10 % less than those obtained using three point bend test specimen for D = 500 mm and 200 mm, respectively.
Abbreviations
- CBM:
-
Crack band model
- CCM:
-
Cohesive crack model
- CT:
-
Compact tension
- DGFM:
-
Double-G fracture model
- DKFM:
-
Double-K fracture model
- ECM:
-
Effective crack model
- FCM:
-
Fictitious crack model
- FPZ:
-
Fracture process zone
- LEFM:
-
Linear elastic fracture mechanics
- SEM:
-
Size effect model
- SIF:
-
Stress intensity factor
- STC:
-
Split tension cube
- TPBT:
-
Three point bend test
- TPFM:
-
Two parameter fracture model
- WST:
-
Wedge splitting test
- a o :
-
Initial crack length
- A i :
-
Regression coefficients
- a c :
-
Effective crack length at peak (critical) load
- B :
-
Width of beam
- B i :
-
Regression coefficients
- c 1, c 2 :
-
Material constants for nonlinear softening function
- CMOD:
-
Crack mouth opening displacement
- CMOD c :
-
Crack mouth opening displacement at critical load
- CTOD:
-
Crack tip opening displacement
- CTODc :
-
Crack tip opening displacement at critical load
- D :
-
Depth or characteristic dimension of specimen
- E :
-
Modulus of elasticity of concrete
- f t :
-
Uniaxial tensile strength of concrete
- G F :
-
Fracture energy of concrete
- G(x,a):
-
Weight function
- H :
-
Height or total depth (2D) for split tension cube specimen
- k(α, β):
-
Non-dimensional function for KI or geometry factor
- K I :
-
Stress intensity factor
- K ini IC :
-
Initial cracking toughness
- K un IC :
-
Unstable fracture toughness
- K CIC :
-
Cohesive toughness
- m(x,a):
-
Universal weight function
- M 1 , M 2 , M 3 :
-
Parameters of weight function
- P u :
-
Maximum applied load or critical load
- S :
-
Span of beam
- t :
-
Half of the width of distributed load for split tension cube specimen
- V(α,β):
-
Dimensionless function for CMOD
- w c :
-
Maximum crack opening displacement at the crack-tip for which the cohesive stress becomes equals to zero
- α :
-
Ratio of crack length to depth of specimen (a/D)
- β :
-
Ratio of load-distributed to height of specimen (2t/h = t/D) for split tension cube specimen
- σ :
-
Cohesive stress
- υ :
-
The Poisson’s ratio
- σ s (CTODc):
-
Cohesive stress at the tip of initial notch corresponding to CTODc
References
Bažant, Z. P., Kim, J.-K., & Pfeiffer, P. A. (1986). Determination of fracture properties from size effect tests. Journal of Structural Engineering ASCE, 112(2), 289–307.
Bažant, Z. P., & Oh, B. H. (1983). Crack band theory for fracture of concrete. Materials and Structures, 16(93), 155–177.
Bueckner, H. F. (1970). A novel principle for the computation of stress intensity factors. Zeitschrift für Angewandte Mathematik und Mechanik, 50, 529–546.
Carpinteri, A. (1989). Cusp catastrophe interpretation of fracture instability. Journal of the Mechanics and Physics of Solids, 37(5), 567–582.
Choubey, R. K., Kumar, S., & Rao, M. C. (2014). Effect of shear-span/depth ratio on cohesive crack and double-K fracture parameters. International Journal of Construction, 2(3), 229–247.
Cusatis, G., & Schauffert, E. A. (2009). Cohesive crack analysis of size effect. Engineering Fracture Mechanics, 76, 2163–2173.
Elices, M., Rocco, C., & Roselló, C. (2009). Cohesive crack modeling of a simple concrete: Experimental and numerical results. Engineering Fracture Mechanics, 76, 1398–1410.
Glinka, G., & Shen, G. (1991). Universal features of weight functions for cracks in Mode I. Engineering Fracture Mechanics, 40, 1135–1146.
Hillerborg, A., Modeer, M., & Petersson, P. E. (1976). Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research, 6, 773–782.
Hu, S., & Lu, J. (2012). Experimental research and analysis on double-K fracture parameters of concrete. Advanced Science Letters, 12(1), 192–195.
Hu, S., Mi, Z., & Lu, J. (2012). Effect of crack-depth ratio on double-K fracture parameters of reinforced concrete. Applied Mechanics and Materials, 226–228, 937–941.
Ince, R. (2010). Determination of concrete fracture parameters based on two-parameter and size effect models using split-tension cubes. Engineering Fracture Mechanics, 77, 2233–2250.
Ince, R. (2012). Determination of the fracture parameters of the Double-K model using weight functions of split-tension specimens. Engineering Fracture Mechanics, 96, 416–432.
Isida, M. (1971). Effect of width and length on stress intensity factor of internally cracked plates under various boundary conditions. International Journal of Fracture, 7, 301–316.
Jenq, Y. S., & Shah, S. P. (1985). Two parameter fracture model for concrete. Journal of Engineering Mechanics, 111(10), 1227–1241.
Karihaloo, B. L., & Nallathambi, P. (1991). Notched beam test: Mode I fracture toughness. In S. P. Shah & A. Carpinteri (Eds.), Fracture mechanics test methods for concrete, report of RILEM Technical Committee 89-FMT (pp. 1–86). London, UK: Chamman & Hall.
Kumar, S. (2010). Behavoiur of fracture parameters for crack propagation in concrete. Ph.D. Thesis submitted to Indian Institute of Technology, Kharagpur, India.
Kumar, S., & Barai, S. V. (2008a). Influence of specimen geometry on determination of double-K fracture parameters of concrete: A comparative study. International Journal of Fracture, 149, 47–66.
Kumar, S., & Barai, S. V. (2008b). Cohesive crack model for the study of nonlinear fracture behaviour of concrete. Journal of the Institution of Engineers (India), 89, 7–15.
Kumar, S., & Barai, S. V. (2009a). Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function. Engineering Fracture Mechanics, 76, 935–948.
Kumar, S., & Barai, S. V. (2009b). Effect of softening function on the cohesive crack fracture parameters of concrete CT specimen. Sadhana-Academy Proceedings in Engineering Sciences, 36(6), 987–1015.
Kumar, S., & Barai, S. V. (2010). Determining the double-K fracture parameters for three-point bending notched concrete beams using weight function. Fatigue & Fracture of Engineering Materials & Structures, 33(10), 645–660.
Kumar, S., & Pandey, S. R. (2012). Determination of double-K fracture parameters of concrete using split-tension cube test. Computers and Concrete, 9(1), 1–19.
Kumar, S., Pandey, S. R., & Srivastava, A. K. L. (2013). Analytical methods for determination of double-K fracture parameters of concrete. Advances in Concrete Construction, 1(4), 319–340.
Kumar, S., Pandey, S. R., & Srivastava, A. K. L. (2014). Determination of double-K fracture parameters of concrete using peak load method. Engineering Fracture Mechanics, 131, 471–484.
Kwon, S. H., Zhao, Z., & Shah, S. P. (2008). Effect of specimen size on fracture energy and softening curve of concrete: Part II. Inverse analysis and softening curve. Cement Concrete Res, 38, 1061–1069.
Lee, J., & Lopez, M. M. (2014). An experimental study on fracture energy of plain concrete. International Journal of Concrete Structures and Materials, 8(2), 129–139.
Modeer, M. (1979). A fracture mechanics approach to failure analyses of concrete materials. Report TVBM-1001, Division of Building Materials. University of Lund, Sweden.
Murthy, A. R., Iyer, N. R., & Prasad, B. K. R. (2012). Evaluation of fracture parameters by Double-G, Double-K models and crack extension resistance for high strength and ultra high strength concrete beams. Computers Materials & Continua, 31(3), 229–252.
Nallathambi, P., & Karihaloo, B. L. (1986). Determination of specimen-size independent fracture toughness of plain concrete. Magazine of Concrete Research, 135, 67–76.
Park, K., Paulino, G. H., & Roesler, J. R. (2008). Determination of the kink point in the bilinear softening model for concrete. Engineering Fracture Mechanics, 7, 3806–3818.
Petersson, P. E. (1981). Crack growth and development of fracture zone in plain concrete and similar materials. Report No. TVBM-100, Lund Institute of Technology, Sweden.
Planas, J., & Elices, M. (1991). Nonlinear fracture of cohesive material. International Journal of Fracture, 51, 139–157.
Reinhardt, H. W., Cornelissen, H. A. W., & Hordijk, D. A. (1986). Tensile tests and failure analysis of concrete. Journal of Structural Engineering, 112(11), 2462–2477.
Rice, J. R. (1972). Some remarks on elastic crack-tip stress fields. International Journal of Solids and Structures, 8, 751–758.
RILEM Draft Recommendation (TC50-FMC). (1985). Determination of fracture energy of mortar and concrete by means of three-point bend test on notched beams. Materials and Structures, 18(4), 287–290.
Roesler, J., Paulino, G. H., Park, K., & Gaedicke, C. (2007). Concrete fracture prediction using bilinear softening. Cement Concrete Composites, 29, 300–312.
Tada, H., Paris, P. C., & Irwin, G. R. (2000). Stress analysis of cracks handbook (3rd ed.). New York, NY: ASME Press.
Timoshenko, S. P., & Goodier, J. N. (1970). Theory of elasticity (3rd ed.). New York, NY: McGraw Hill.
Wu, Z., Jakubczak, H., Glinka, G., Molski, K., & Nilsson, L. (2003). Determination of stress intensity factors for cracks in complex stress fields. Archive of Mechanical Engineering, 50(1), s41–s67.
Xu, S., & Reinhardt, H. W. (1998). Crack extension resistance and fracture properties of quasi-brittle materials like concrete based on the complete process of fracture. International Journal of Fracture, 92, 71–99.
Xu, S., & Reinhardt, H. W. (1999a). Determination of double-K criterion for crack propagation in quasi-brittle materials, Part I: Experimental investigation of crack propagation. International Journal of Fracture, 98, 111–149.
Xu, S., & Reinhardt, H. W. (1999b). Determination of double-K criterion for crack propagation in quasi-brittle materials, Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams. International Journal of Fracture, 98, 151–177.
Xu, S., & Reinhardt, H. W. (1999c). Determination of double-K criterion for crack propagation in quasi-brittle materials, Part III: Compact tension specimens and wedge splitting specimens. International Journal of Fracture, 98, 179–193.
Xu, S., & Reinhardt, H. W. (2000). A simplified method for determining double-K fracture meter parameters for three-point bending tests. International Journal of Fracture, 104, 181–209.
Xu, S., & Zhang, X. (2008). Determination of fracture parameters for crack propagation in concrete using an energy approach. Engineering Fracture Mechanics, 75, 4292–4308.
Xu, S., & Zhu, Y. (2009). Experimental determination of fracture parameters for crack propagation in hardening cement paste and mortar. International Journal of Fracture, 157, 33–43.
Zhang, X., & Xu, S. (2011). A comparative study on five approaches to evaluate double-K fracture toughness parameters of concrete and size effect analysis. Engineering Fracture Mechanics, 78, 2115–2138.
Zhang, X., Xu, S., & Zheng, S. (2007). Experimental measurement of double-K fracture parameters of concrete with small-size aggregates. Frontiers of Architecture and Civil Engineering in China, 1(4), 448–457.
Zhao, Z., Kwon, S. H., & Shah, S. P. (2008). Effect of specimen size on fracture energy and softening curve of concrete: Part I. Experiments and fracture energy. Cement Concrete Res, 38, 1049–1060.
Zhao, Y., & Xu, S. (2002). The influence of span/depth ratio on the double-K fracture parameters of concrete. Journal of China Three Gorges University (Natural Sciences), 24(1), 35–41.
Zi, G., & Bažant, Z. P. (2003). Eignvalue method for computing size effect of cohesive cracks with residual stress, with application to kink-bands in composites. International Journal of Engineering Science, 41, 1519–1534.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pandey, S.R., Kumar, S. & Srivastava, A.K.L. Determination of Double-K Fracture Parameters of Concrete Using Split-Tension Cube: A Revised Procedure. Int J Concr Struct Mater 10, 163–175 (2016). https://doi.org/10.1007/s40069-016-0139-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40069-016-0139-6