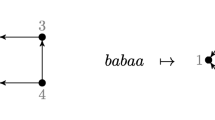On a cohomology of digraphs and Hochschild cohomology

Abstract

We use a differential form cohomology theory on transitive digraphs to give a new proof of a theorem of Gerstenhaber and Schack about isomorphism between simplicial cohomology and Hochschild cohomology of a certain algebra associated with the simplicial complex.

1 Introduction

At present time there exist different notions of homology (cohomology) of digraphs and undirected graphs, see [2, 5, 6, 8, 10, 11]. In this paper we use cohomology theory of digraphs of [2, 6], that is reminiscent of the classical de Rham cohomology theory of differential forms, in order to give a new proof of a theorem of Gerstenhaber and Schack [4]. In the course of the proof we obtain close relations between the cohomologies of digraphs, those of simplicial complexes, and the Hochschild cohomologies of algebras [9].

Let $\mathbb {K}$ be a commutative unital ring and $A\$be an associative unital algebra over a $\mathbb {K}$. Denote by $C^{n}\left( A\right)$ the set of all $\mathbb {K}$-multilinear functions $f:A^{n}\rightarrow A$. Hochschild [9] introduced a differential $D:C^{n}\left( A\right) \rightarrow C^{n+1}\left( A\right)$ that satisfies $D^{2}=0$ thus making $\left\{ C^{n}\left( A\right) \right\} _{n=0}^{\infty }$ into a cochain complex. Its cohomologies are called Hochschild cohomologies of $A$ and are denoted by $HH^{n}\left( A\right) .$

In 1983 Gerstenhaber and Schack [4] established the following beautiful relation between the Hochschild and simplicial cohomologies. Let $S$ be a (finite) simplicial complex. Denote by $V$ the set of all barycenters of the simplexes of $S$, and introduce on $V$ a structure of a digraph (=directed graph) by defining the edges $a\rightarrow b$ between two barycenters $a,b\in V$ as follows: if $s_{a}$ is the simplex whose barycenter is $a$, and $s_{b}$ the simplex with the barycenter $b$, then by definition

$$\begin{aligned} a\rightarrow b\Leftrightarrow s_{a}\supset s_{b}. \end{aligned}$$

(1)

In particular, the underlying undirected graph of $V$ with removed loops is the $1$-skeleton of the barycentric subdivision $B_{S}$ of $S$ (see Fig. 1).

Fig. 1

The barycentric subdivision $B_{S}$ of a 2-simplex (left) and the associated digraph $\left( V,\rightarrow \right)$ (right)

Denote by $A$ the left $\mathbb {K}$-module of all formal linear combinations of the edges of $V$ with coefficients from $\mathbb {K}$. Define the multiplication of the edges by

$$\begin{aligned} \left( a,b\right) \left( a^{\prime },b^{\prime }\right) =\left\{ \begin{array}{ll} \left( a,b^{\prime }\right) , \quad &{} \text {if }b=a^{\prime } \\ 0, \quad &{} \text {otherwise,} \end{array} \right. \end{aligned}$$

(2)

(cf. Fig. 2) and then extend it by $\mathbb {K}$-bilinearly to a multiplication in $A$, thus making $A$ into an associative algebra over $\mathbb {K}$. The algebra $A$ has a unity that is the sum of all loops in $V$.

Fig. 2

Illustration to (2): $\left( a,b\right) \left( a^{\prime },b^{\prime }\right) =\left( a,b^{\prime }\right)$ (left) and $\left( a,b\right) \left( a^{\prime },b^{\prime }\right) =0$ (right)

Gerstenhaber and Schack proved in [4] that

$$\begin{aligned} HH^{*}\left( A\right) \cong H^{*}\left( S\right) , \end{aligned}$$

(3)

where $H^{*}\left( S\right)$ is the simplicial cohomology of $S$. Although they constructed in [4] an explicit cochain map $\tau :C^{*}\left( S\right) \rightarrow C^{*}\left( A\right) ,$ they wrote: “we are unable to show by direct calculation that $H^{*}\left( \tau \right)$ is an isomorphism”. To prove the isomorphism (3) in cohomologies, the Gerstenhaber and Schack [3] used instead the cohomology comparison theorem developed in their previous paper.

Another proof of (3) was given by Cibils [1] using a cleverly chosen resolution of the path algebra of a poset associated with the simplicial complex.

The purpose of this paper is to give a direct proof of (3) by constructing a cochain map between $C^{*}\left( S\right)$ and $C^{*}\left( A\right)$, although in a number of steps, and showing that the associated cohomology map is an isomorphism, thus completing the program of Gerstenhaber and Schack.

Let us briefly describe our approach. We make a crucial use of cohomologies of digraphs that are analogous to the differential forms cohomologies. The elements of the cochain complex $\Omega ^{n}$, based on the digraph $\left( V,\rightarrow \right)$, are $\mathbb {K}$-valued functions on $n$-paths $i_{0}\rightarrow i_{1}\rightarrow \cdots \rightarrow i_{n}$ of the vertices of $V$, with appropriately defined exterior differential $d:\Omega ^{n}\rightarrow \Omega ^{n+1}.$ We use also a regularized cochain complex $\Omega _{reg}^{*}$ where the functions are defined only on the paths $i_{0}\rightarrow i_{1}\rightarrow \cdots \rightarrow i_{n}$ with distinct vertices.

The notions of exterior differential and exterior forms on general digraphs as well as the associated cohomology theory were developed in [2, 5, 6]. In particular, it was shown in [6] (based on [7]) that the cohomology groups $H^{*}\left( \Omega _{reg},\mathbb {Z}\right)$ are homotopy invariant. We refer the reader to [5, 6] for general overview of (co)homology theories on digraphs. In the present paper we need the aforementioned theory only in a special case of transitive digraphs. In the latter case the definitions of the cochain complex and the associated cohomologies are significantly simplified and can be easily introduced from scratch as we do in Sect. 3.

Consider the product $\widetilde{V}=V\times V$ that also becomes a digraph with the following definition of edges:

$$\begin{aligned} \left( i,j\right) \rightarrow \left( i^{\prime },j^{\prime }\right) \ \quad \text { in } \quad \widetilde{V}\Leftrightarrow j\rightarrow i^{\prime } \quad \text { in } \quad V \end{aligned}$$

(see Sect. 4). This type of product of graphs is unusual in graph theory, but is appropriate for our purpose. On the digraph $( \widetilde{V},\rightarrow )$ we also introduce a cochain complex $\widetilde{ \Omega }^{*}$ analogously to the cochain complex $\Omega ^{*}$ on $\left( V,\rightarrow \right)$, with an additional weight in the exterior differential, which strengthens the role of the diagonal ${\mathrm {diag}} \widetilde{V}\cong V$.

Denote by $\overline{A}$ the algebra spanned by all pairs $\left( a,b\right) \!\in \! V\times V$ (not only edges of $V$) with multiplication (2), and consider a Hochschild cohomology $HH^{*}(A,\overline{A})$ that comes from the cochain complex $C^{*}(A,\overline{A})$ of multilinear functions $f:A^{n}\rightarrow \overline{A}.$

We prove (3) by means of the following chain of relations:

$$\begin{aligned} HH^{*}\left( A\right) \! \cong \! HH^{*}(A,\overline{A})\!\cong \! H^{*}( \widetilde{\Omega })\!\cong \! H^{*}\left( \Omega \right) \!\cong \! H^{*}\left( \Omega _{reg}\right) \!\cong \! H^{*}\left( B_{S}\right) \!\cong \! H^{*}\left( S\right) ,\nonumber \\ \end{aligned}$$

(4)

where $B_{S}\$is the barycentric subdivision of $S$. The corresponding cochain complexes are related as follows:

$$\begin{aligned} C^{*}\left( A\right) \subset C^{*}\left( A,\overline{A}\right) \cong \widetilde{\Omega }^{*}\succ \Omega ^{*}\succ \Omega _{reg}^{*}\cong C^{*}\left( B_{S}\right) \supset C^{*}\left( S\right) , \end{aligned}$$

where $\mathcal {A}^{*}\succ \mathcal {B}^{*}$ means that $\mathcal {B} ^{*}$ is a quotient cochain complex of $\mathcal {A}^{*}$. Hence, in the first step we enlarge the cochain complex in question, but in each of the following steps we reduce it while preserving cohomologies, until we arrive at $C^{*}\left( S\right) .$ Let us comment on each of the relations in (4).

• 1. The the isomorphism $H^{*}(\widetilde{\Omega })\cong H^{*}(\Omega )$ is key result of this paper and is proved in Lemma 4.2. We establish first a map between the corresponding cochain complexes and then prove that the cohomology of the kernel of this map is trivial. This step is crucial in the entire proof as it allows to drastically reduce the cochain complex $\widetilde{\Omega }^{*}$ to $\Omega ^{*}$.

• 2. The isomorphism $HH^{*}(A,\overline{A})\cong H^{*}(\widetilde{ \Omega })$ follows from the isomorphism of the corresponding cochain complexes $C^{*}(A,\overline{A})$ and $\widetilde{\Omega }^{*}$. The proof of the latter contains a trick of changing the tensor notation, which in an instant transforms the elements of $C^{n}(A,\overline{A})$ into those of $\widetilde{\Omega }^{n}$ (Lemma 5.1).

• 3. The isomorphism $HH^{*}(A)\cong HH^{*}\left( A,\overline{A} \right)$ is proved in Lemma 5.2 using an argument from the proof of Lemma 4.2.

• 4. The isomorphism $H^{*}\left( \Omega \right) \cong H^{*}\left( \Omega _{reg}\right)$ is proved in Lemma 6.1, also similarly to Lemma 4.2.

• 5. The isomorphism $H^{*}\left( \Omega _{reg}\right) \cong H^{*}\left( B_{S}\right)$ is rather straightforward and follows from the isomorphism of the cochain complexes $\Omega _{reg}^{*}$ and $C^{*}\left( B_{S}\right)$ (Lemma 7.1).

• 5. The isomorphism $H^{*}\left( B_{S}\right) \cong H^{*}\left( S\right)$ is classical.

The structure of the paper is determined by the above sequence of lemmas. The main Theorem 7.2 is stated and proved at the end of the paper.

2 Hochschild cohomology

Let $\mathbb {K}$ be a commutative unital ring and $A$ be an associative unital algebra over $\mathbb {K}$. Let $M$ be a left $\mathbb {K}$-module that has a compatible structure of a $A$-bimodule (in particular, $M$ can be an algebra over $\mathbb {K}$ containing $A$ as a subalgebra). For any non-negative integer $n$, denote by $C^{n}\left( A,M\right)$ the set of all $\mathbb {K}$-multilinear functions $f:A^{n}\rightarrow M$. Clearly, $C^{n}\left( A,M\right)$ is a left $\mathbb {K}$-module. By definition, we take $C^{0}\left( A,M\right) =M$.

Consider the Hochschild differential $D:C^{n}\left( A,M\right) \rightarrow C^{n+1}\left( A,M\right)$ defined on any function $f\in C^{n}\left( A,M\right)$ as follows:

$$\begin{aligned} Df\left( a_{1},a_{2},\ldots ,a_{n+1}\right)= & {} a_{1}f\left( a_{2},\ldots ,a_{n+1}\right) \\&+\sum _{k=1}^{n}\left( -1\right) ^{k}f\left( a_{1},\ldots ,a_{k}a_{k+1},\ldots a_{n+1}\right) \\&+\left( -1\right) ^{n+1}f\left( a_{1},\ldots ,a_{n}\right) a_{n+1}, \end{aligned}$$

for all $a_{i}\in A$. In particular, for $n=0$, the differential of a constant $f=m\in M$ is a function $Df:A\rightarrow M$ given by

$$\begin{aligned} Df\left( a\right) =am-ma. \end{aligned}$$

It is known [9] that $D^{2}=0$ so that we have a cochain complex

$$\begin{aligned} 0\rightarrow C^{0}\left( A,M\right) \overset{D}{\rightarrow } \cdots \overset{D}{ \rightarrow }C^{n}\left( A,M\right) \overset{D}{\rightarrow }C^{n+1}\left( A,M\right) \overset{D}{\rightarrow } \cdots \end{aligned}$$

whose cohomologies are called the Hochschild cohomologies and are denoted by $HH^{*}\left( A,M\right) .$

3 Cohomology of transitive digraphs

In this section we introduce a cohomology theory on transitive digraphs, similarly to the cohomology theory of digraph of [2, 6]. However, unlike the cited works, we allow the digraphs to have loop edges, which is motivated by application to Hochschild cohomology.

Let $V$ be a finite set, whose elements will be called vertices. Denote by $\Lambda ^{n}=\Lambda ^{n}\left( V,\mathbb {K}\right)$ the left $\mathbb {K}$ -module of all functions $f:V^{n+1}\rightarrow \mathbb {K}$. We use the following notation

$$\begin{aligned} f_{i_{0} \ldots i_{n}}:=f\left( i_{0}, \ldots ,i_{n}\right) \end{aligned}$$

for all $i_{k}\in V$. Any sequence $i_{0} \ldots i_{n}$ of $n+1$ vertices of $V$ will be called an $n$-path. Hence, any $f\in \Lambda ^{n}$ is a $\mathbb {K}$-valued function on $n$-paths.

Fix a function $\delta :V\rightarrow \mathbb {K}$ and define the exterior differential $d:\Lambda ^{n}\rightarrow \Lambda ^{n+1}$ by

$$\begin{aligned} \left( df\right) _{i_{0} \ldots i_{n+1}}=\displaystyle \sum \limits _{k=0}^{n+1}\left( -1\right) ^{k}\delta _{i_{k}}f_{i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}}, \end{aligned}$$

(5)

where the hat $\widehat{i_{k}}$ means omission of the index $i_{k}$. Strictly speaking, the operator $d$ should have been denoted by $d_{\delta }$ but we omit the index $\delta$ as usually this causes no confusion.

Claim

$d^{2}=0.$

Proof

For any $f\in \Lambda ^{n}$, we have

$$\begin{aligned} \left( d^{2}f\right) _{i_{0} \ldots i_{n+2}}= & {} \displaystyle \sum \limits _{k=0}^{n+2}\left( -1\right) ^{k}\delta _{i_{k}}\left( df\right) _{i_{0} \ldots \widehat{i_{k}} \ldots i_{n+2}} \\= & {} \displaystyle \sum \limits _{k=0}^{n+2}\left( -1\right) ^{k}\delta _{i_{k}}\left( \sum _{l=0}^{k-1}\left( -1\right) ^{l}\delta _{i_{l}}f_{i_{0} \ldots \widehat{i_{l} } \ldots \widehat{i_{k}} \ldots i_{n+2}}\right. \nonumber \\&\left. +\sum _{l=k+1}^{n+2}\left( -1\right) ^{l-1}\delta _{i_{l}}f_{i_{0} \ldots \widehat{i_{k}} \ldots \widehat{i_{l}} \ldots i_{n+2}}\right) \\= & {} \sum _{0\le l<k\le n+2}\left( -1\right) ^{k+l}\delta _{i_{k}}\delta _{i_{l}}f_{i_{0} \ldots \widehat{i_{l}} \ldots \widehat{i_{k}} \ldots i_{n+2}} \\&-\sum _{0\le k<l\le n+2}\left( -1\right) ^{k+l}\delta _{i_{k}}\delta _{i_{l}}f_{i_{0} \ldots \widehat{i_{k}} \ldots \widehat{i_{l}} \ldots i_{n+2}}. \end{aligned}$$

After switching $k$ and $l$ in the last sum we see that it is equal to the previous one, whence $d^{2}f=0$ follows. $\square$

Hence, we obtain a cochain complex

$$\begin{aligned} 0\rightarrow \Lambda ^{0}\overset{d}{\rightarrow } \cdots \overset{d}{\rightarrow }\Lambda ^{n}\overset{d}{\rightarrow }\Lambda ^{n+1}\overset{d}{\rightarrow } \cdots \end{aligned}$$

So far $V$ was just a finite set. Let us now introduce a digraph structure on $V$.

Definition 3.1

A couple $\left( V,E\right)$ is called a (finite) digraph if $V$ is any finite set and $E\subset V\times V$ is a relation on $V$.

Any couple $\left( i,j\right) \in E$ is called a directed edge or arrow and will be denoted by $i\rightarrow j$. A digraph $\left( V,E\right)$ will also be denoted by $\left( V,\rightarrow \right)$.

Definition 3.2

A $n$-path $i_{0} \ldots i_{n}$ of vertices of a digraph $\left( V,\rightarrow \right)$ is called allowed if

$$\begin{aligned} i_{0}\rightarrow i_{1}\rightarrow \cdots \rightarrow i_{n}, \end{aligned}$$

and non-allowed otherwise.

On any digraph $\left( V,\rightarrow \right)$ there is a natural way of defining a cochain complex $\Omega ^{*}$ with the exterior differential $d$ that takes into account allowed paths (see [6, 8]). However, we need this construction only for a specific class of transitive digraphs, that can be done easily as below.

Definition 3.3

Let $\left( V,\rightarrow \right)$ be a digraph and let $\delta$ be a $\mathbb {K}$-valued function on $V$. We say that $V$ is a $\delta$-transitive if

$$\begin{aligned} i\rightarrow j\ \quad \text {and} \quad j\rightarrow k\Rightarrow i\rightarrow k, \quad \text {provided} \quad \delta _{j}\ne 0, \end{aligned}$$

for all $i,j,k\in V$.

Let $\left( V,\rightarrow \right)$ be a $\delta$-transitive digraph. Denote by $\Omega ^{n}=\Omega ^{n}\left( \left( V,\rightarrow \right) , \mathbb {K}\right)$ the set of $\mathbb {K}$-valued functions on all allowed $n$-paths on $V$. Let us use the same function $\delta$ in the definition (5) of $d$ and show that the operator $d=d_{\delta }$ can be considered as an operator from $\Omega ^{n}$ to $\Omega ^{n+1}$. Indeed, given $f\in \Omega ^{n},$ let us first extend $f$ arbitrarily to a function on all $n$-paths, that is, to an element of $\Lambda ^{n}$. Then (5) defines $df$ as an element of $\Lambda ^{n+1}$, that is, a function on all $\left( n+1\right)$-paths. Then the restriction of $df$ to the allowed $\left( n+1\right)$-paths yields an element of $\Omega ^{n+1},$ that will also be denoted by $df$.

Claim

If $V$ is $\delta$-transitive then, for any $f\in \Omega ^{n}$, the differential $df$ is well defined as an element of $\Omega ^{n+1}.$

Proof

We need to show that $df$ on allowed $\left( n+1\right)$-paths does not depend on how $f$ was extended. Indeed, let $i_{0} \ldots i_{n+1}$ be an allowed path. We need to verify that in the right hand side of (5) the contribution of the terms $\delta _{i_{k}}f_{i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}}$ with non-allowed paths $i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}$ vanishes. Indeed, if $\delta _{i_{k}}=0$ then this term does not give any contribution. If $\delta _{i_{k}}\ne 0$ then $i_{k-1}\rightarrow i_{k}\rightarrow i_{k+1}$ imply $i_{k-1}\rightarrow i_{k+1}$ so that the $n$ -path

$$\begin{aligned} i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}=i_{0} \ldots i_{k-1}i_{k+1} \ldots i_{n+1} \end{aligned}$$

is allowed, which finishes the proof. $\square$

Hence, we obtain a cochain complex

$$\begin{aligned} 0\rightarrow \Omega ^{0}\overset{d}{\rightarrow } \cdots \overset{d}{\rightarrow } \Omega ^{n}\overset{d}{\rightarrow }\Omega ^{n+1}\overset{d}{\rightarrow } \cdots \end{aligned}$$

of the $\delta$-transitive digraph $\left( V,\rightarrow \right)$ that will be denoted by $\Omega ^{*}=\Omega _{\delta }^{*}\left( \left( V,\rightarrow \right) ,\mathbb {K}\right)$. The cohomologies of this complex

$$\begin{aligned} H^{n}\left( \Omega \right) =H_{\delta }^{n}\left( \Omega \left( V,\rightarrow \right) ,\mathbb {K}\right) =\hbox {ker} d|_{\Omega ^{n}}/{\mathrm {Im}}d|_{\Omega ^{n-1}} \end{aligned}$$

(where $n\ge 0$) are of primary interest for us.

Note that a digraph can be $\delta$-transitive with many choices of function $\delta$ since in Definition 3.3 only the support of $\delta$ matters. However, since we use the same function $\delta$ also in the definition (5) of $d$, different choices of $\delta$ will determine different complexes $\Omega ^{*}$. Therefore, in applications one should carefully specify the choice of $\delta$.

A digraph $\left( V,\rightarrow \right)$ is called transitive if

$$\begin{aligned} i\rightarrow j\rightarrow k\Rightarrow i\rightarrow k. \end{aligned}$$

For example, any partially ordered set (shortly, a poset) is a transitive digraph. Of course, a digraph is transitive if and only if it is $\delta$-transitive with $\delta \equiv 1.$ For transitive digraphs we will always use $\delta \equiv 1$ in the definition (5) of $d$.

The cochain complex $H^{*}\left( \Omega \right)$ for transitive graphs is a particular case of the construction of [6, 8] of cochain complexes for arbitrary digraphs. Note also that the ring $\mathbb {K}$ in the definition of the cochain complex can be replaced by any abelian additive group provided the function $\delta$ is $\mathbb {Z}$-valued.

4 Self-product of a transitive digraph

Let $\left( V,\rightarrow \right)$ be a transitive digraph, and $\Omega ^{*}$ the associated cochain complex (with $\delta \equiv 1$ as we have agreed above). Set $\widetilde{V}=V\times V$ and define the edges on $\widetilde{V}$ as follows

$$\begin{aligned} \left( i,j\right) \rightarrow \left( i^{\prime },j^{\prime }\right) \Leftrightarrow j\rightarrow i^{\prime } \end{aligned}$$

(6)

for all $i,j,i^{\prime },j^{\prime }\in V$ (cf. Fig. 3).

Fig. 3

An example of digraphs $V$ and $\widetilde{V}$

Define a function $\delta :\widetilde{V}\rightarrow \mathbb {K}$ by

$$\begin{aligned} \delta _{\left( i,j\right) }=\left\{ \begin{array}{l@{\quad }l} 1, &{} i=j, \\ 0, &{} i\ne j. \end{array} \right. \end{aligned}$$

(7)

Claim

If $\left( V,\rightarrow \right)$ is transitive then $(\widetilde{V} ,\rightarrow )$ is $\delta$-transitive with the function $\delta$ defined by (7).

Proof

Indeed, if

$$\begin{aligned} \left( i,j\right) \rightarrow \left( i^{\prime },j^{\prime }\right) \rightarrow \left( i^{\prime \prime },j^{\prime \prime }\right) \end{aligned}$$

and $\delta _{\left( i^{\prime },j^{\prime }\right) }\ne 0$ then $i^{\prime }=j^{\prime }$ and

$$\begin{aligned} j\rightarrow i^{\prime }=j^{\prime }\rightarrow i^{\prime \prime } \end{aligned}$$

whence $j\rightarrow i^{\prime \prime }$ and, hence, $\left( i,j\right) \rightarrow \left( i^{\prime \prime },j^{\prime \prime }\right)$. $\square$

Definition 4.1

The $\delta$-transitive digraph $\widetilde{V}$ is called a self-product of $V$.

As before, let $\Omega ^{*}$ be the cochain complex of the transitive digraph $V$, and denote by $\widetilde{\Omega }^{*}$ the cochain complex of the $\delta$-transitive digraph $\widetilde{V}.$

We say that a digraph $\left( V,\rightarrow \right)$ is reflexive if $i\rightarrow i$ for all $i\in V$. For example, any poset is transitive and reflexive. Now we can state and prove our main technical lemma.

Lemma 4.2

If $V$ is transitive and reflexive, then we have the isomorphism of cohomologies:

$$\begin{aligned} H^{*}(\widetilde{\Omega })\cong H^{*}(\Omega ). \end{aligned}$$

(8)

Proof

Let us identify $V$ with ${\mathrm {diag}}\widetilde{V}$. Note that $\left( i,i\right) \rightarrow \left( j,j\right)$ is equivalent to $i\rightarrow j$ so that $\mathop {\mathrm {diag}}\widetilde{V}$ as a subgraph of $\widetilde{V}$ is isomorphic to a digraph $V$. For any function $f$ on the allowed $n$-paths in $\widetilde{V}$, let $\Phi f$ be a restriction of $f$ to the allowed $n$-paths on $V$. In tensor notation, any function $f\in \widetilde{\Omega } ^{n}$ has the components $f_{\left( i_{0},j_{0}\right) \ldots \left( i_{n},j_{n}\right) },$ and then $\Phi f$ is defined by

$$\begin{aligned} \left( \Phi f\right) _{i_{0} \ldots i_{n}}=f_{\left( i_{0},i_{0}\right) \ldots \left( i_{n},i_{n}\right) } \end{aligned}$$

for all allowed $n$-paths $i_{0} \ldots i_{n}$ on $V$. Hence, we obtain an epimorphism

$$\begin{aligned} \Phi :\widetilde{\Omega }^{n}\rightarrow \Omega ^{n}. \end{aligned}$$

(9)

We start with verifying that the following diagram is commutative:

$$\begin{aligned} \begin{array}{lll} \widetilde{\Omega }^{n} &{} \overset{d}{\rightarrow } &{} \widetilde{\Omega } ^{n+1} \\ \ \downarrow ^{\Phi } &{} &{} \downarrow ^{\Phi } \\ \Omega ^{n} &{} \overset{d}{\rightarrow } &{} \Omega ^{n+1} \end{array} \end{aligned}$$

(10)

For any $f\in \widetilde{\Omega }^{n}$ and any allowed $\left( n+1\right)$-path $i_{0} \ldots i_{n+1}$ on $V$ we have

$$\begin{aligned} \left( d\left( \Phi f\right) \right) _{i_{0} \ldots i_{n+1}}= & {} \displaystyle \sum \limits _{k=0}^{n+1}\left( -1\right) ^{k}\left( \Phi f\right) _{i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}} \\= & {} \displaystyle \sum \limits _{k=0}^{n+1}\left( -1\right) ^{k}\delta _{\left( i_{k},i_{k}\right) }f_{\left( i_{0},i_{0}\right) \ldots \widehat{(i_{k},i_{k})} \ldots \left( i_{n+1},i_{n+1}\right) } \\= & {} \left( df\right) _{\left( i_{0},i_{0}\right) \ldots \left( i_{n+1},i_{n+1}\right) } \\= & {} \left( \Phi \left( df\right) \right) _{i_{0} \ldots i_{n+1}} \end{aligned}$$

whence $d\Phi =\Phi d$ follows.

Denote by $K^{n}$ the kernel of the mapping (9). Since $\Phi$ is a cochain map from $\widetilde{\Omega }^{*}$ to $\Omega ^{*}$, we see that $K^{*}$ is a sub cochain complex. The short exact sequence

$$\begin{aligned} 0\rightarrow K^{*}\rightarrow \widetilde{\Omega }^{*}\rightarrow \Omega ^{*}\rightarrow 0 \end{aligned}$$

of cochain complexes yields by zigzag Lemma the long exact sequence in cohomologies

$$\begin{aligned} \cdots \rightarrow H^{n}\left( K\right) \rightarrow H^{n}(\widetilde{\Omega } )\rightarrow H^{n}\left( \Omega \right) \rightarrow H^{n+1}\left( K\right) \rightarrow \cdots \end{aligned}$$

Hence, in order to prove the isomorphism (8) it suffices to show that, for all non-negative integers $n$,

$$\begin{aligned} H^{n}\left( K\right) \cong \left\{ 0\right\} , \end{aligned}$$

that is, if $f\in K^{n}$ and $df=0$ then there is $g\in K^{n-1}$ such that $f=dg$.

Let us denote the elements of $\widetilde{V}$ by $\mathbf {i}_{1},\mathbf {i} _{2}$ etc. If $\mathbf {i=}\left( i,j\right)$ then set

$$\begin{aligned} \mathbf {i}^{\prime }=\left( j,j\right) \in {\mathrm {diag}}\widetilde{V} \end{aligned}$$

so that $\mathbf {i}^{\prime }$ can be regarded as “projection” of $\mathbf {i}$ onto $V$. Note that always $\mathbf {i}\rightarrow \mathbf {i}^{\prime }$, which follows from the reflexivity of $V$, and

$$\begin{aligned} \mathbf {i\rightarrow j\ \Leftrightarrow i}^{\prime }\rightarrow \mathbf {j} \end{aligned}$$

for all $\mathbf {i,j}\in \widetilde{V},$ since $\mathbf {i}$ and $\mathbf {i} ^{\prime }$ have the same second component.

The following claim is a key to the proof.

Claim

For any $f\in \widetilde{\Omega }^{n}$ there exists $g\in \widetilde{\Omega } ^{n-1}$ such that the following holds:

• (i) for any allowed $\left( n-1\right)$-path $\mathbf { i}_{1} \ldots \mathbf {i}_{n}$ that lies on ${diag}\widetilde{V}$,

  $$\begin{aligned} g_{\mathbf {i}_{1} \ldots \mathbf{i}_{n}}=0; \end{aligned}$$

  (11)

• (ii) for any allowed $n$-path $\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}$ on $\widetilde{V}$ that does not lie entirely on ${\mathrm {diag}}\widetilde{V}$,

  $$\begin{aligned} \left( -1\right) ^{k}\left( df\right) _{\mathbf{i}_{1} \ldots \mathbf{i}_{k} \mathbf{i}_{k}^{\prime } \ldots \mathbf{i}_{n+1}}=f_{\mathbf{i}_{1} \ldots \mathbf{i} _{n+1}}-\left( dg\right) _{\mathbf{i}_{1} \ldots \mathbf{i}_{n+1}}, \end{aligned}$$

  (12)

  where $k$ is the smallest index such that $\mathbf {i}_{k}\notin {\mathrm {diag}} \widetilde{V}.$

Let us define $g$ as follows: for any allowed $\left( n-1\right)$-paths $\mathbf {i}_{1} \ldots \mathbf {i}_{n}$ on $\widetilde{V}$, set $g_{\mathbf {i} _{1} \ldots \mathbf {i}_{n}}=0$ if all $\mathbf {i}_{k}\in {\mathrm {diag}}\widetilde{V}$ , whereas otherwise set

$$\begin{aligned} g_{\mathbf {i}_{1} \ldots \mathbf {i}_{n}}=\left( -1\right) ^{k}f_{\mathbf {i}_{1} \ldots \mathbf {i}_{k-1}\mathbf {i}_{k}\mathbf {i}_{k}^{\prime }\mathbf {i}_{k+1} \ldots \mathbf {i}_{n}}~, \end{aligned}$$

(13)

where $k$ is the minimal index such that $\mathbf {i}_{k}\notin \mathop {\mathrm {diag}} \widetilde{V}$. Observe that the right hand side of (13) is well defined, since the $n$-path $\mathbf {i}_{1} \ldots \mathbf {i}_{k-1}\mathbf {i}_{k} \mathbf {i}_{k}^{\prime }\mathbf {i}_{k+1} \ldots \mathbf {i}_{n}$ is allowed whenever $\mathbf {i}_{1} \ldots \mathbf {i}_{n}$ is allowed, because $\mathbf {i} _{k}\rightarrow \mathbf {i}_{k}^{\prime }\rightarrow \mathbf {i}_{k+1}$ (see Fig. 4).

Fig. 4

The path $\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime }\mathbf {i}_{k+1} \ldots$ is allowed

We have by (5)

$$\begin{aligned} \left( dg\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}=\sum _{l=1}^{n+1}\left( -1\right) ^{l-1}\delta _{\mathbf {i}_{l}}g_{\mathbf {i}_{1} \ldots \widehat{\mathbf { i}_{l}} \ldots \mathbf {i}_{n+1}}. \end{aligned}$$

(14)

The term $\delta _{\mathbf {i}_{l}}g_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l} } \ldots \mathbf {i}_{n+1}}$ in (14) vanishes whenever $\delta _{\mathbf {i} _{l}}=0$, which, in particular, is the case when $l=k$ as $\mathbf {i} _{k}\notin {\mathrm {diag}}\widetilde{V}.$ Assume that $\delta _{\mathbf {i} _{l}}\ne 0,$ in particular, $l\ne k$. Then the $\left( n-1\right)$-path $\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}$ is allowed. The first term in this path outside ${\mathrm {diag}}\widetilde{V}$ is again $\mathbf {i}_{k}$, and it has the ordinal number $k-1$ in this path, if $l<k$, and the ordinal number $k$ if $l>k$. Hence, if $l<k,$ then we obtain by (13)

$$\begin{aligned} g_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}}=\left( -1\right) ^{k-1}f_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{k} \mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}}, \end{aligned}$$

and if $l>k$ then

$$\begin{aligned} g_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}}=\left( -1\right) ^{k}f_{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}}. \end{aligned}$$

Combining all the terms together, we obtain

$$\begin{aligned} \left( dg\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}= & {} \sum _{l=1}^{k-1}\left( -1\right) ^{k+l}\delta _{\mathbf {i}_{l}}f_{\mathbf {i}_{1} \ldots \widehat{\mathbf { i}_{l}} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i} _{n+1}}\nonumber \\&+\sum _{l=k+1}^{n+1}\left( -1\right) ^{k+l-1}\delta _{\mathbf {i} _{l}}f_{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \widehat{ \mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}}. \end{aligned}$$

(15)

By (5) we have also

$$\begin{aligned} \left( df\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}}= & {} \sum _{l=1}^{k-1}\left( -1\right) ^{l-1}\delta _{\mathbf { i}_{l}}f_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{k}\mathbf {i }_{k}^{\prime } \ldots \mathbf {i}_{n+1}} \\&+\left( -1\right) ^{k-1}\delta _{\mathbf {i}_{k}}f_{\mathbf {i}_{1} \ldots \widehat{\mathbf {i}_{k}}~\mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}} \\&+\left( -1\right) ^{k}\delta _{\mathbf {i}_{k}^{\prime }}f_{\mathbf {i} _{1} \ldots \mathbf {i}_{k}\widehat{\mathbf {i}_{k}^{\prime }} \ldots \mathbf {i}_{n+1}}\\&+\sum _{l=k+1}^{n+1}\left( -1\right) ^{l}\delta _{\mathbf {i}_{l}}f_{\mathbf { i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \widehat{\mathbf {i}_{l}} \ldots \mathbf {i}_{n+1}} \end{aligned}$$

Noticing that $\delta _{\mathbf {i}_{k}}=0$, $\delta _{\mathbf {i}_{k}^{\prime }}=1$, $f_{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\widehat{\mathbf {i}_{k}^{\prime }} \ldots \mathbf {i}_{n+1}}=f_{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}$, substituting here (15) and multiplying by $\left( -1\right) ^{k}$, we obtain (12).

Now assuming that $f\in K^{n}$ and $df=0,$ let us show that the function $g$ defined by (13) belongs to $K^{n-1}$ and satisfies $dg=f.$ That $g\in K^{n-1}$ is true by (11). Let us show that $dg=f$, that is, for any allowed $n$-path $\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}$,

$$\begin{aligned} \left( dg\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}=f_{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}. \end{aligned}$$

(16)

If all $\mathbf {i}_{1}, \ldots ,\mathbf {i}_{n+1}\in {\mathrm {diag}}\widetilde{V}$ then we have by (11) that $\left( dg\right) _{\mathbf {i}_{1} \ldots \mathbf { i}_{n+1}}=0$, which matches $f_{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}=0$ that is true by $f\in K^{n}$. Otherwise, let $k$ be the minimal value of the index such that $\mathbf {i}_{k}\notin {\mathrm {diag}}\widetilde{V}.$ As it was observed above, the $\left( n+1\right)$-path $\mathbf {i}_{1} \ldots \mathbf {i} _{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}$ is allowed. Since $df=0$, that is, $df$ vanishes on all allowed $\left( n+1\right)$-paths, we obtain

$$\begin{aligned} \left( df\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}}=0. \end{aligned}$$

Substituting this into (12), we obtain (16). $\square$

5 Algebra associated with poset

A digraph $\left( V,\rightarrow \right)$ is called a poset (partially ordered set) if it is reflexive, transitive, and antisymmetric, that is, $i\rightarrow j\rightarrow i$ implies $i=j.$ In this section $\left( V,\rightarrow \right)$ is always a finite poset.

Denote by $\overline{A}$ the left $\mathbb {K}$-module of all formal $\mathbb { K}$-linear combinations of pairs $\left( i,j\right)$ of vertices of $V$. The pair $\left( i,j\right)$ as an element of $\overline{A}$ will be denoted by $e_{ij}$ so that any element $a\in \overline{A}$ can be uniquely represented in the form

$$\begin{aligned} a=\sum _{i,j\in V}a^{ij}e_{ij} \end{aligned}$$

where $a^{ij}$ are the coefficients from $\mathbb {K}$. Let $A$ be a submodule of $\overline{A}$ spanned by all $e_{ij}$ with $i\rightarrow j$; that is, any $a\in A$ has the form

$$\begin{aligned} a=\sum _{\left\{ i,j\in V:i\rightarrow j\right\} }a^{ij}e_{ij}. \end{aligned}$$

Define in $\overline{A}$ multiplication on the basis elements

$$\begin{aligned} e_{ij}\cdot e_{i^{\prime }j^{\prime }}=\delta _{ji^{\prime }}e_{ij^{\prime }}=\left\{ \begin{array}{l@{\quad }l} e_{ij^{\prime }}, &{} \text {if }i^{\prime }=j, \\ 0, &{} \text {otherwise,} \end{array} \right. \end{aligned}$$

(17)

where

$$\begin{aligned} \delta _{ij}=\left\{ \begin{array}{l@{\quad }l} 1,&{} i=j, \\ 0,&{} i\ne j, \end{array} \right. \end{aligned}$$

(18)

and then extend the multiplication to all the elements of $\overline{A}$ by $\mathbb {K}$-bilinearity. It follows from (17) that, for all $a,b\in \overline{A}$ and $i,j\in V$,

$$\begin{aligned} \left( ab\right) ^{ij}=\sum _{l\in V}a^{il}b^{lj}. \end{aligned}$$

(19)

It is easy to see that $\overline{A}$ is an associative algebra over $\mathbb {K}$ with a unity $1_{\overline{A}}=\sum _{i\in V}e_{ii}.$

By a poset property we see that if $e_{ij},e_{kl}\in A$ then $e_{ij}e_{kl}\in A$ so that $A$ is a subalgebra of $\overline{A}$ (and $1_{A}=1_{\overline{A}}$). Hence, the Hochschild cochain complex $C^{*}(A, \overline{A})$ is well defined as in Sect. 2.

On the other hand, we have a cochain complex $\Omega ^{*}$ of the poset $V$ as defined in Sect. 3, and a cochain complex $\widetilde{ \Omega }^{*}$ of the self-product $\widetilde{V}$ of $V$ as defined in Sect. 4.

Lemma 5.1

The cochain complexes $C^{*}(A,\overline{A})$ and $\widetilde{\Omega }^{*}$ are isomorphic.

Proof

For any function $f\in C^{n}(\overline{A},\overline{A})$ set

$$\begin{aligned} f_{i_{1}j_{1}i_{2}j_{2} \ldots i_{n}j_{n}}=f\left( e_{i_{1}j_{1}}, \ldots ,e_{i_{n}j_{n}}\right) \end{aligned}$$

for all $i_{k},j_{k}\in V$. Since $f$ takes values in $\overline{A}$, $f_{i_{1}j_{1}i_{2}j_{2} \ldots i_{n}j_{n}}$ is linear combination of the terms $e_{ij}$ as follows:

$$\begin{aligned} f_{i_{1}j_{1}i_{2}j_{2} \ldots i_{n}j_{n}}=\sum _{i,j\in V}f_{i_{1}j_{1}i_{2}j_{2} \ldots i_{n}j_{n}}^{ij}e_{ij} \end{aligned}$$

with the coefficients $f_{i_{1}j_{1}i_{2}j_{2} \ldots i_{n}j_{n}}^{ij}\in \mathbb { K}$. It follows that, for all $a_{1}, \ldots ,a_{n}\in A$,

$$\begin{aligned} f\left( a_{1}, \ldots ,a_{n}\right) =\sum f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ij}a_{1}^{i_{1}j_{1}} \ldots a_{n}^{i_{n}j_{n}}e_{ij} \end{aligned}$$

where the summation is performed over all $i,j,i_{k},j_{k}\in V$.

By definition of the Hochschild differential $D$ on $C^{*}(\overline{A}, \overline{A})$ we have

$$\begin{aligned} \left( Df\right) _{i_{1}j_{1} \ldots i_{n+1}j_{n+1}}= & {} \left( Df\right) \left( e_{i_{1}j_{1}}, \ldots ,e_{i_{n+1}j_{n+1}}\right) \\= & {} e_{i_{1}j_{1}}f\left( e_{i_{2}j_{2}}, \ldots ,e_{i_{n+1}j_{n+1}}\right) \\&+\sum _{k=1}^{n}\left( -1\right) ^{k}f\left( e_{i_{1}j_{1}}, \ldots ,e_{i_{k}j_{k}}\cdot e_{i_{k+1}j_{k+1}}, \ldots e_{i_{n+1}j_{n+1}}\right) \\&+\left( -1\right) ^{n+1}f\left( e_{i_{1}j_{1}}, \ldots ,e_{i_{n}j_{n}}\right) e_{i_{n+1}j_{n+1}}. \end{aligned}$$

Using (17) and (19) we obtain

$$\begin{aligned} \left( Df\right) _{i_{1}j_{1} \ldots i_{n+1}j_{n+1}}^{ij}= & {} \sum _{l\in V}e_{i_{1}j_{1}}^{il}f_{i_{2}j_{2} \ldots i_{n+1}j_{n+1}}^{lj} \\&+\sum _{k=1}^{n}\left( -1\right) ^{k}\delta _{j_{k}i_{k+1}}f_{i_{1}j_{1} \ldots i_{k-1}j_{k-1}i_{k}j_{k+1}i_{k+2}j_{k+2} \ldots i_{n+1}j_{n+1}}^{ij}\\&+\left( -1\right) ^{n+1}\sum _{l\in V}f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{il}e_{i_{n+1}j_{n+1}}^{lj} \end{aligned}$$

whence

$$\begin{aligned} \left( Df\right) _{i_{1}j_{1} \ldots i_{n+1}j_{n+1}}^{ij}= & {} \delta _{ii_{1}}f_{i_{2}j_{2} \ldots i_{n+1}j_{n+1}}^{j_{1}j} \\&+\sum _{k=1}^{n}\left( -1\right) ^{k}\delta _{j_{k}i_{k+1}}f_{i_{1}j_{1} \ldots i_{k-1}j_{k-1}i_{k}j_{k+1}i_{k+2}j_{k+2} \ldots i_{n+1}j_{n+1}}^{ij}\\&+\left( -1\right) ^{n+1}\delta _{j_{n+1}j}f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ii_{n+1}}. \end{aligned}$$

Now we change notation, namely, we rename $f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ij}$ to $f_{ii_{1}j_{1} \ldots i_{n}j_{n}j}$ and then rename in the latter the indices as follows: $f_{i_{0}j_{0}i_{1}j_{1} \ldots i_{n}j_{n}}.$ Effectively this means the following change of notation:

$$\begin{aligned} i\rightsquigarrow i_{0},\quad i_{k}\rightsquigarrow j_{k-1},\quad j_{k}\rightsquigarrow i_{k},\quad j\rightsquigarrow j_{n}. \end{aligned}$$

In the notation for $Df$ we should use $j\rightsquigarrow j_{n+1}$ instead of $j\rightsquigarrow j_{n}$, so that the above formula for $Df$ becomes:

$$\begin{aligned} \left( Df\right) _{i_{0}j_{0} \ldots i_{n+1}j_{n+1}}= & {} \delta _{i_{0}j_{0}}f_{i_{1}j_{1} \ldots i_{n+1}j_{n+1}} \\&+\sum _{k=1}^{n}\left( -1\right) ^{k}\delta _{i_{k}j_{k}}f_{i_{0}j_{0} \ldots i_{k-1}j_{k-1}i_{k+1}j_{k+1} \ldots i_{n+1}j_{n+1}}\\&+\left( -1\right) ^{n+1}\delta _{i_{n+1}j_{n+1}}f_{i_{0}j_{0} \ldots i_{n}j_{n}}. \end{aligned}$$

All pairs $\left( i_{k},j_{k}\right)$ can be regarded as elements of $\widetilde{V}=V\times V$. Using notation

$$\begin{aligned} \mathbf {i}_{k}=\left( i_{k},j_{k}\right) \end{aligned}$$

we see that the components of $f$ can be denoted by $f_{\mathbf {i}_{0} \ldots \mathbf {i}_{n}}$. Hence, the above formula for $Df$ can be rewritten as follows

$$\begin{aligned} \left( Df\right) _{\mathbf {i}_{0} \ldots \mathbf {i}_{n+1}}=\sum _{k=0}^{n+1}\left( -1\right) ^{k}\delta _{\mathbf {i}_{k}}f_{\mathbf {i}_{0} \ldots \widehat{\mathbf {i} _{k}} \ldots \mathbf {i}_{n+1}} \end{aligned}$$

(20)

for all $\mathbf {i}_{k}\in \widetilde{V}$. Consequently, any function $f\in C^{n}(\overline{A},\overline{A})$ can be identified with a function from $\Lambda ^{n}(\widetilde{V})$, this identification is clearly a linear isomorphism, and it transforms the operator $D$ to $d$ as one can see from comparison of (20) and (5) [note that we use the same the function $\delta$ in (20) and (5)].

Consider now the set $C^{n}\left( A,\overline{A}\right)$. The functions from $C^{n}\left( A,\overline{A}\right)$ can be regarded as restrictions of the functions from $C^{n}\left( \overline{A},\overline{A}\right)$ to the domain $A^{n}$. In particular, for any $f\in C^{n}(A,\overline{A})$, the value $f\left( e_{i_{1}j_{1}}, \ldots ,e_{i_{n}j_{n}}\right)$ is defined only if $i_{k}\rightarrow j_{k}$, for all $k=1, \ldots ,n$. Hence, the component $f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ij}$ is defined also under the same condition, that is, for the sequences of indices such that

$$\begin{aligned} ii_{1}\rightarrow j_{1}i_{2}\rightarrow j_{2} \ldots i_{n}\rightarrow j_{n}j. \end{aligned}$$

In the notation $f_{i_{0}j_{0} \ldots i_{n}j_{n}}=f_{\mathbf {i}_{0} \ldots \mathbf {i} _{n}}$ this condition becomes $j_{k-1}\rightarrow i_{k}$, that is,

$$\begin{aligned} i_{0}j_{0}\rightarrow i_{1}j_{1}\rightarrow \cdots \rightarrow i_{n}j_{n}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \mathbf {i}_{0}\rightarrow \mathbf {i}_{1}\rightarrow \cdots \rightarrow \mathbf {i} _{n}, \end{aligned}$$

given that the edges in $\widetilde{V}$ are defined by (6). Hence, any function $f\in C^{n}(A,\overline{A})$ is identified with a $\mathbb {K}$-valued function on allowed $n$-paths on $\widetilde{V}$, and such functions are exactly the elements of $\widetilde{\Omega }^{n}$, which proves the isomorphism of the cochain complexes $C^{*}(A,\overline{A})$ and $\widetilde{\Omega }^{*}$. $\square$

Lemma 5.2

We have $HH^{*}(A,A)\cong HH^{*}\left( A,\overline{A} \right)$.

Proof

In the previous proof we have identified the set $C^{n}\left( A,\overline{A} \right)$ with the set $\widetilde{\Omega }^{n}$ of functions on allowed $n$ -paths on $\widetilde{V}$. The set $C^{n}\left( A,A\right)$ is a subset of $C^{n}\left( A,\overline{A}\right)$, and a function $f\in C^{n}\left( A, \overline{A}\right)$ belongs to $C^{n}\left( A,A\right)$ if and only if, for all $i_{1}\rightarrow j_{1}, \ldots ,i_{n}\rightarrow j_{n}$,

$$\begin{aligned} i\not \rightarrow j\Rightarrow f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ij}=0 \end{aligned}$$

(21)

(in other words, the component $f^{ij}$ vanishes if $ij$ is not an edge). Let $\widetilde{\Omega }_{0}^{n}$ be the image of $C^{n}\left( A,A\right)$ in $\widetilde{\Omega }^{n}$. Then we have the isomorphism of the cochain complexes

$$\begin{aligned} C^{*}\left( A,\overline{A}\right) \cong \widetilde{\Omega }^{*} \quad \text {and} \quad C^{*}\left( A,A\right) \cong \widetilde{\Omega }_{0}^{*}. \end{aligned}$$

It suffices to prove that

$$\begin{aligned} H^{n}(\widetilde{\Omega })\cong H^{n}(\widetilde{\Omega }_{0}), \end{aligned}$$

which is equivalent to

$$\begin{aligned} H^{n}(\widetilde{\Omega }/\widetilde{\Omega }_{0})=\left\{ 0\right\} . \end{aligned}$$

(22)

Before we can prove (22), let us reformulate the property (21) in terms of the notation $f_{\mathbf {i}_{0} \ldots \mathbf {i}_{n}}$ that we use for the elements of $\widetilde{\Omega }^{n}$. Let us introduce one more relation $\twoheadrightarrow$ on $\widetilde{V}$:

$$\begin{aligned} \left( i,j\right) \twoheadrightarrow \left( i^{\prime },j^{\prime }\right) \Leftrightarrow i\rightarrow j^{\prime } \end{aligned}$$

[observe the difference with the definition (6) of $\rightarrow$ on $\widetilde{V}$]. Then the relation $i\rightarrow j$ in the notation $f_{i_{1}j_{1} \ldots i_{n}j_{n}}^{ij}$ is equivalent to $\mathbf {i} _{0}\twoheadrightarrow \mathbf {i}_{n}$ in the notation $f_{\mathbf {i}_{0} \ldots \mathbf {i}_{n}}.$

We say that an allowed $n$-path $\mathbf {i}_{0} \ldots \mathbf {i}_{n}$ on $\widetilde{V}$ is proper if $\mathbf {i}_{0}\twoheadrightarrow \mathbf { i}_{n}$, and improper otherwise. Then it follows from (21) that a function $f\in \widetilde{\Omega }^{n}$ belongs to $\widetilde{\Omega }_{0}^{n}$ if and only if

$$\begin{aligned} f_{\mathbf {i}_{0} \ldots \mathbf {i}_{n}}=0 \quad \text {for any allowed improper}\,\,n \text {-path} \quad \mathbf {i}_{0} \ldots \mathbf {i}_{n}\text {.}\ \end{aligned}$$

(23)

To prove (22) we need to show that if $f\in \widetilde{\Omega }^{n}$ and $df\in \widetilde{\Omega }_{0}^{n+1}$ then there exists $g\in \widetilde{ \Omega }^{n-1}$such that $dg-f\in \widetilde{\Omega }_{0}^{n}$. Define $g\in \widetilde{\Omega }^{n-1}$ as in Claim in the proof of Lemma 4.2. Then we must show that, for any allowed improper $n$-path $\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}$ on $\widetilde{V}$,

$$\begin{aligned} \left( dg\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}=f_{\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}}\ . \end{aligned}$$

(24)

An improper path cannot lie entirely on ${\mathrm {diag}}\widetilde{V}$ as otherwise $\mathbf {i}_{1}\rightarrow \cdots \rightarrow \mathbf {i}_{n+1}$ implies $\mathbf {i}_{1}\rightarrow \mathbf {i}_{n+1}$ and $\mathbf {i} _{1}\twoheadrightarrow \mathbf {i}_{n+1}$. Let $k$ be the smallest index with $\mathbf {i}_{k}\notin {\mathrm {diag}}\widetilde{V}$. Then $g$ satisfies (12), and the identity (24) will follow from (12) if we show that

$$\begin{aligned} \left( df\right) _{\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i}_{n+1}}=0. \end{aligned}$$

(25)

The path $\mathbf {i}_{1} \ldots \mathbf {i}_{k}\mathbf {i}_{k}^{\prime } \ldots \mathbf {i }_{n+1}$ is allowed, so that we obtain (25) from $df\in \widetilde{ \Omega }_{0}^{n+1}$ if we show that this path is improper. If $k<n+1$ then it is improper because its first and last vertices are the same as those of the improper path $\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}.$ In the case $k=n+1$ we need to verify that the path $\mathbf {i}_{1} \ldots \mathbf {i}_{n+1}\mathbf {i} _{n+1}^{\prime }$ is improper, that is, Indeed, since the last components of $\mathbf {i}_{n+1}$ and $\mathbf {i}_{n+1}^{\prime }$ are the same, the condition follows from $\square$

6 Regularized cohomologies of posets

A $n$-path $i_{0} \ldots i_{n}$ of the vertices of a digraph $\left( V,\rightarrow \right)$ is called regular if $i_{k-1}\ne i_{k}$ for all $k=1, \ldots ,n,$ and irregular otherwise. Let from now on $\left( V,\rightarrow \right)$ be a poset. Any the regular allowed $n$-path $i_{0} \ldots i_{n}$ on a poset has an additional property that all the vertices $i_{k}$ in this path are distinct. Indeed, if $i_{l}=i_{k}$ for some $l<k-1$ then $i_{l}\rightarrow i_{l+1}\rightarrow \cdots i_{k-1}\rightarrow i_{k}$ implies by transitivity that $i_{l}\rightarrow i_{k-1}\rightarrow i_{k}$ whence by a poset property $i_{k-1}=i_{k}$, which contradicts the regularity.

Alongside the set $\Omega ^{n}$ of $\mathbb {K}$-valued functions on all allowed $n$-paths on $V$, consider the set $\Omega _{reg}^{n}$ of $\mathbb {K}$-valued functions on all regular allowed $n$-paths. Observe that $d\Omega _{reg}^{n}\subset \Omega _{reg}^{n+1}$ in the following sense: any function $f\in \Omega _{reg}^{n}$ can be extended to a function from $\Omega ^{n}$, also denoted by $f$, then $df$ on the regular allowed $\left( n+1\right)$-paths does not depend on the choice of extension. Indeed, if $i_{0} \ldots i_{n+1}$ is a regular allowed $\left( n+1\right)$-path then

$$\begin{aligned} \left( df\right) _{i_{0} \ldots i_{n+1}}=\sum _{k=0}^{n+1}\left( -1\right) ^{k}f_{i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}}, \end{aligned}$$

(26)

and each path $i_{0} \ldots \widehat{i_{k}} \ldots i_{n+1}$ is regular and allowed. Hence, $\Omega _{reg}^{*}$ is a cochain complex, that will be referred to as the regularized cochain complex of the poset $V$.

Lemma 6.1

If $V$ is a poset then

$$\begin{aligned} H^{*}\left( \Omega \right) \cong H^{*}\left( \Omega _{reg}\right) . \end{aligned}$$

(27)

Proof

Consider the mapping $\Omega ^{n}\rightarrow \Omega _{reg}^{n}$ that is given by restriction of the functions from $\Omega ^{n}$ to regular allowed paths. Let $K^{n}$ be the kernel of this mapping, so that we have a short exact sequence

$$\begin{aligned} 0\rightarrow K^{*}\rightarrow \Omega ^{*}\rightarrow \Omega _{reg}^{*}\rightarrow 0. \end{aligned}$$

Hence, the isomorphism (27) will follow if we prove that

$$\begin{aligned} H^{n}\left( K\right) \cong \left\{ 0\right\} , \end{aligned}$$

that is, for any $f\in K^{n}$ with $df=0$ there is $g\in K^{n-1}$ such that $dg=f$.

If $n=0$ then $K^{0}=\left\{ 0\right\}$ so the claim is trivial. For $n=1$, a function $f\in K^{1}$ may have non-zero components only of the form $f_{ii}$. Since $\left( df\right) _{iii}=f_{ii}$, it follows from $df=0$ that also $f_{ii}=0$ so that $f=0.$ Hence, $g=0$ is a solution.

Assume $n\ge 2$. We will construct explicitly a solution $g\in K^{n-1}$ of the equation $df=g$. Let us first illustrate this construction in the case $n=2$. For any allowed $1$-path $i\rightarrow j$, set

$$\begin{aligned} g_{ij}=\left\{ \begin{array}{ll} 0, &{} i\ne j \\ f_{iii}, &{} i=j. \end{array} \right. \end{aligned}$$

Then $g\in K^{1}$ and let us show that $dg=f,$ that is,

$$\begin{aligned} \left( dg\right) _{ijk}=f_{ijk} \end{aligned}$$

(28)

for all allowed paths $ijk.$ If the path $ijk$ is regular then all $i,j,k$ are distinct, and

$$\begin{aligned} \left( dg\right) _{ijk}=g_{jk}-g_{ik}+g_{ij}=0=f_{ijk}. \end{aligned}$$

If $i=j$ then

$$\begin{aligned} \left( dg\right) _{iik}=g_{ii}=f_{iii}. \end{aligned}$$

Since $df=0$, we have

$$\begin{aligned} 0=\left( df\right) _{iiik}=f_{iik}-f_{iii} \end{aligned}$$

whence

$$\begin{aligned} \left( dg\right) _{iik}=f_{iik}. \end{aligned}$$

Similarly one treats the case $j=k$, which settles (28).

Now consider the general case $n\ge 2$. If $i_{0} \ldots i_{n-1}$ is a regular allowed path then set

$$\begin{aligned} g_{i_{0} \ldots i_{n-1}}=0. \end{aligned}$$

If $i_{0} \ldots i_{n-1}$ is an irregular allowed path then let $k$ be the smallest index with the property that $i_{k}=i_{k+1}.$ Denoting by $j$ the common value of $i_{k}$ and $i_{k+1}$, we can write

$$\begin{aligned} i_{0} \ldots i_{n-1}=i_{0} \ldots i_{k-1}jji_{k+2} \ldots i_{n-1}. \end{aligned}$$

Then set

$$\begin{aligned} g_{i_{0} \ldots i_{n-1}}=\left( -1\right) ^{k}f_{i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n-1}}. \end{aligned}$$

(29)

Note that the $n$-path $i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n-1}$ on the right hand side is obtained by inserting one more vertex $j$ between already existing in $i_{0} \ldots i_{n-1}$ two vertices $j$ at positions $k$ and $k+1$ (see Fig. 5).

By definition, we have $g\in K^{n-1}$. Let us show that $dg=f$ in $\Omega ^{n},$ that is,

$$\begin{aligned} \left( dg\right) _{i_{0} \ldots i_{n}}=f_{i_{0} \ldots i_{n}} \end{aligned}$$

(30)

for any allowed path $i_{0} \ldots i_{n}.$ If the path $i_{0} \ldots i_{n}$ is regular then

$$\begin{aligned} \left( dg\right) _{i_{0} \ldots i_{n}}=\sum _{l=0}^{n}\left( -1\right) ^{l}g_{i_{0} \ldots \widehat{i_{l}} \ldots i_{n}}=0, \end{aligned}$$

because all the paths $i_{0} \ldots \widehat{i_{l}} \ldots i_{n}$ are also regular. Since also $f_{i_{0} \ldots i_{n}}=0$ by $f\in K^{n}$, we obtain the identity (30) in this case.

Let now the path $i_{0} \ldots i_{n}$ be irregular. Let $k$ be the smallest index with the property $i_{k}=i_{k+1},$ and denote by $j$ the common value of $i_{k}$ and $i_{k+1}$, that is,

$$\begin{aligned} i_{0} \ldots i_{n}=i_{0} \ldots i_{k-1}jji_{k+2} \ldots i_{n}. \end{aligned}$$

Observe that the $k$-path $i_{0} \ldots i_{k}$ is regular and allowed, which implies that all the vertices in this path are distinct. We have by (26)

$$\begin{aligned} \left( dg\right) _{i_{0} \ldots i_{n}}= & {} \sum _{l=0}^{k-1}\left( -1\right) ^{l}g_{i_{0} \ldots \widehat{i_{l}} \ldots jj \ldots i_{n}} \end{aligned}$$

(31)

$$\begin{aligned}&+\left( -1\right) ^{k}g_{i_{0} \ldots \widehat{j}j \ldots i_{n}}+\left( -1\right) ^{k+1}g_{i_{0} \ldots j\widehat{j} \ldots i_{n}} \end{aligned}$$

(32)

$$\begin{aligned}&+\sum _{l=k+2}^{n}\left( -1\right) ^{l}g_{i_{0} \ldots jj \ldots \widehat{i_{l}} \ldots i_{n}} \end{aligned}$$

(33)

Clearly, the two terms in (32) cancel out. Observe that in the paths $i_{0} \ldots \widehat{i_{l}} \ldots jj \ldots i_{n}$ and $i_{0} \ldots jj \ldots \widehat{i_{l}} \ldots i_{n}$ the first couple of equal consecutive vertices is $jj$, the same as in the full paths $i_{0} \ldots jj \ldots i_{n}.$ By (29) we obtain

$$\begin{aligned} g_{i_{0} \ldots \widehat{i_{l}} \ldots jj \ldots i_{n}}=\left( -1\right) ^{k-1}f_{i_{0} \ldots \widehat{i_{l}} \ldots jjj \ldots i_{n}} \end{aligned}$$

and

$$\begin{aligned} g_{i_{0} \ldots jj \ldots \widehat{i_{l}} \ldots i_{n}}=\left( -1\right) ^{k}f_{i_{0} \ldots jjj \ldots \widehat{i_{l}} \ldots i_{n}} \end{aligned}$$

whence

$$\begin{aligned} \left( dg\right) _{i_{0} \ldots i_{n}}=\sum _{l=0}^{k-1}\left( -1\right) ^{l+k-1}f_{i_{0} \ldots \widehat{i_{l}} \ldots jjj \ldots i_{n}}+\sum _{l=k+2}^{n}\left( -1\right) ^{l+k}f_{i_{0} \ldots jjj \ldots \widehat{i_{l}} \ldots i_{n}}. \end{aligned}$$

(34)

On the other hand, since the $\left( n+1\right)$-path $i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n}$ is allowed, we have

$$\begin{aligned} \left( df\right) _{i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n}}=0. \end{aligned}$$

(35)

Computing this component by (26), we obtain

$$\begin{aligned} \left( df\right) _{i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n}}= & {} \sum _{l=0}^{k-1}\left( -1\right) ^{l}f_{i_{0} \ldots \widehat{i_{l}} \ldots jjj \ldots i_{n}} \end{aligned}$$

(36)

$$\begin{aligned}&+\left( -1\right) ^{k}f_{i_{0} \ldots \widehat{j}jj \ldots i_{n}}+\left( -1\right) ^{k+1}f_{i_{0} \ldots j\widehat{j}j \ldots i_{n}}\nonumber \\&+\left( -1\right) ^{k+2}f_{i_{0} \ldots jj \widehat{j} \ldots i_{n}} \end{aligned}$$

(37)

$$\begin{aligned}&+\sum _{l=k+2}^{n}\left( -1\right) ^{l+1}f_{i_{0} \ldots jjj \ldots \widehat{i_{l}} \ldots i_{n}} \end{aligned}$$

(38)

The three terms in (37) sum up to $\left( -1\right) ^{k}f_{i_{0} \ldots jj \ldots i_{n}}=\left( -1\right) ^{k}f_{i_{0} \ldots i_{n}}.$ Combining (36)–(38) with (34), we obtain

$$\begin{aligned} \left( df\right) _{i_{0} \ldots i_{k-1}jjji_{k+2} \ldots i_{n}}=\left( -1\right) ^{k-1}\left( dg\right) _{i_{0} \ldots i_{n}}+\left( -1\right) ^{k}f_{i_{0} \ldots i_{n}}. \end{aligned}$$

Substituting here (35), we obtain (30). $\square$

Fig. 5

Paths $i_{0} \ldots jj \ldots i_{n-1}$ and $i_{0} \ldots jjj \ldots i_{n-1}$

7 Poset associated with a simplicial complex

Let $S$ be a finite simplicial complex. By definition, $S$ can be regarded as a family of subsets of a finite set $M$ such that if $s\in S$ then any non-empty subset $t$ of $s$ also belongs to $S$ (we do not allow the empty set to be in $S$). Then we obtain immediately a poset structure on $S$ as follows:

$$\begin{aligned} s\rightarrow t \Leftrightarrow s\supset t. \end{aligned}$$

Let $B_{S}$ be the barycentric subdivision of $S$ and let $V$ be the set of vertices of $B_{S}$, that is, $V$ is the set of the barycenters of all simplexes of $S$. For any vertex $i\in V$ denote by $s_{i}$ the simplex from $S$ whose barycenter is $i$. Clearly, the set $V$ has the same poset structure as $S$: if $i$ and $i$ are two vertices from $V$ then we set

$$\begin{aligned} i\rightarrow j \Leftrightarrow s_{i}\supset s_{j} \end{aligned}$$

(cf. Fig. 1). As in Sect. 6, let $\Omega _{reg}^{*}$ be a regularized cochain complex of the poset $V$.

Lemma 7.1

We have isomorphism

$$\begin{aligned} H^{*}\left( \Omega _{reg}\right) \cong H^{*}\left( S\right) . \end{aligned}$$

(39)

Proof

We will show that the chain complexes $\Omega _{*}^{reg}$ and $C_{*}\left( B_{S}\right)$ are isomorphic. This will implies the isomorphism of the corresponding cochain complexes and, hence,

$$\begin{aligned} H^{*}\left( \Omega _{reg}\right) \cong H^{*}\left( B_{S}\right) . \end{aligned}$$

Since $H^{*}\left( B_{s}\right) \cong H^{*}\left( S\right)$, the isomorphism (39) will follows.

The set $\Omega _{n}^{reg}$ consists of all formal $\mathbb {K}$-linear combination of the regular allowed $n$-paths $i_{0} \ldots i_{n}$ on $V$. The $n$ -path $i_{0} \ldots i_{n}$ as an element of $\Omega _{n}^{reg}$ will be denoted by $e_{i_{0} \ldots i_{n}}$. The boundary operator $\partial :\Omega _{n}^{reg}\rightarrow \Omega _{n-1}^{reg}$ is defined by

$$\begin{aligned} \partial e_{i_{0} \ldots i_{n}}=\sum _{k=0}^{n}\left( -1\right) ^{k}e_{i_{0} \ldots \widehat{i_{k}} \ldots i_{n}} \end{aligned}$$

(40)

(observe that the $\left( n-1\right)$-path $i_{0} \ldots \widehat{i_{k}} \ldots i_{n}$ is regular allowed). It is clear that $\Omega _{reg}^{n}$ can be regarded as the set of all $\mathbb {K}$-linear functionals on $\Omega _{n}^{reg}$, and it is easy to check that $\partial$ is dual to $d:\Omega _{reg}^{n-1}\rightarrow \Omega _{reg}^{n}$.

By construction of the barycentric subdivision $B_{S}$ of $S$, each regular allowed $n$-path $i_{0} \ldots i_{n}$ in $V$ gives rise to a $n$-simplex of $B_{S}$ with the vertices $i_{0} \ldots i_{n}$, and vice versa (see Fig. 6).

Since the boundary operator on simplexes is defined by

$$\begin{aligned} \partial \left[ i_{0}, \ldots ,i_{n}\right] =\sum _{k=0}^{n}\left( -1\right) ^{k}[i_{0}, \ldots ,\widehat{i_{k}}\ , \ldots ,i_{n}] \end{aligned}$$

that matches (40), we see that the chain complexes $\Omega _{*}^{reg}$ and $C_{*}\left( B_{S}\right)$ are isomorphic, which was to be proved. $\square$

Fig. 6

A regular allowed path $i_{0}i_{1}i_{2}$ determines a $2$-simplex $\left[ i_{0},i_{1},i_{2}\right]$ of $B_{S}$

As in Sect. 2, define the algebras $A$ and $\overline{A}$ based on a poset $V$ and the associated Hochschild cohomologies $HH^{n}\left( A,A\right) .$ Now we can state and prove the main result.

Theorem 7.2

We have the following isomorphism of cohomologies

$$\begin{aligned} HH^{*}\left( A,A\right) \cong H^{*}\left( S\right) , \end{aligned}$$

where $H^{*}\left( S\right)$ is the simplicial cohomologies of the simplicial complex $S$.

Proof

This follows from Lemmas 4.2, 5.1, 5.2, 6.1, 7.1 as in (4). $\square$