Triality, characteristic classes, $D_4$ and $G_2$ singularities

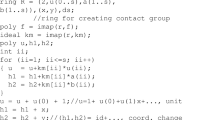
Abstract

We recall the construction of triality automorphism of $\mathfrak {so}(8)$ given by E. Cartan and we give a matrix representation for the real form $\mathfrak {so}(4,4)$. We compute the induced results on the characteristic classes. Paralelly we study the triality automorphism of the singularity $D_4$ (in Arnolds classification of smooth functions) and its miniversal deformation. The similarity with Lie theory leads us to a definition of $G_2$ singularity.

The Lie algebra $\mathfrak {so}(8)$ is the first algebra of the series $D_4,D_5,D_6,\dots$. It is a classical simple algebra but it is also considered exceptional since it is the only one which admits an automorphism of order three. The automorphism of the Lie algebra lifts to an automorphism of the Lie group ${\textit{Spin}}(8)$, the universal cover of $SO(8)$. The fixed point set of that automorphism is the exceptional group $G_2$. Cartan [9] has constructed a concrete triality automorphism for the real compact form of $\mathfrak {so}(8)$. It seems that the approach of E. Cartan to triality was almost forgotten. We think it is worth to recall the original construction. In the “Appendix” we give a formula for the choice of a quadratic form with signature $(4,-4)$. It has the advantage, that the root spaces coincides with the coordinates of the matrix.

We give formulas for the action of triality on the characteristic classes for ${\textit{Spin}}(8)$-bundles. It is remarkable, that the space spanned by the Euler classes of the natural representation and spin representations $S^+$, $S^-$ is a two-dimensional nontrivial representation of $\mathbb {Z}_3$. In other words the sum of the Euler classes is equal to zero and $\mathbb {Z}_3$ permutes the Euler classes cyclically. The remaining generators of the ring of characteristic classes can be chosen to be invariant (except the case when the base field is of characteristic three).

The Dynkin diagram $D_4$ also appears in the singularity theory. The singularity of the type $D_4$ defined by $x^3-3xy^2$ admits an automorphism of order three. Moreover this automorphism can be extended to an automorphism of the parameter space of the miniversal deformation. The action of the triality automorphism on the functions on the parameter space is the same as the action on the cohomology of $H^*({\textit{BSpin}}(8);\mathbb {R})$. Taking the quotient by the cyclic group $\mathbb {Z}_3$ we obtain a map germ $\mathbb {C}^2/\mathbb {Z}_3\rightarrow \mathbb {C}$ with a two-dimensional cohomology of the Milnor fiber. In the distinguished basis of vanishing cycles the intersections are described by the Dynkin diagram $G_2$. We study the geometry and topology of that singularity. Here the domain of the function is singular; it has an isolated singularity of the type $A_2$, and taking a ramified cover, the function itself becomes the classical singularity of type $A_2$. Therefore we can say that the singularity $G_2$ is in some sense built from two singularities $A_2$. This resembles the picture of the root system of the Lie algebra $\mathfrak {g}_2$ which contains two copies of the systems $A_2$ intertwined together.

We wish to put an emphasis on similarities between the theory of Lie algebras and the singularity theory. The formulas for triality in both theories are formally the same, although they describe objects of completely different natures.

1 The original approach of Elie Cartan

In 1925 Cartan published a paper under the title Le principe de dualité et la théorie des groupes simples et semi-simples [9]. In fact the main subject of the article is not duality but a symmetry of order three. After a general introduction motivated by the duality in the matrix group $GL(n)$

$$\begin{aligned} A\mapsto (A^T)^{-1} \end{aligned}$$

Cartan introduced a very concrete automorphism of the Lie algebra $\mathfrak {so}(8)$. The construction of the transformation is the following: Let $(a_{i,j})_{0\le i,j \le 7}\in \mathfrak {so}(8)$ be an antisymmetric matrix. For each $i\in \{1,2,\dots , 7\}$ the quadruple

$$\begin{aligned} a_{0,i},\;a_{i+1,i+5},\;a_{i+4,i+6},\;a_{i+2,i+3} \end{aligned}$$

is transformed linearly by the matrix

$$\begin{aligned} \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} -\frac{1}{2} \;&{}-\frac{1}{2} \;&{} -\frac{1}{2} \;&{} -\frac{1}{2} \;\\ \\ \frac{1}{2}\;&{} \frac{1}{2} \;&{} -\frac{1}{2} \;&{}-\frac{1}{2} \;\\ \\ \frac{1}{2}\;&{} -\frac{1}{2} \;&{} \frac{1}{2} \;&{}-\frac{1}{2} \;\\ \\ \frac{1}{2} \;&{} -\frac{1}{2} \;&{} -\frac{1}{2} \;&{} \frac{1}{2}\; \end{array}\right) \end{aligned}$$

(1)

Here the index $i$ is understood modulo 7. The value $i=0$ plays a special role and it is excluded from the cycle $1,2,\dots 7$. The resulting self-map $\phi :\mathfrak {so}(8)\rightarrow \mathfrak {so}(8)$ is of order three, that is $\phi \circ \phi \circ \phi =Id$ and, what is the most important, it preserves the Lie bracket. The subalgebra $\mathfrak {so}(8)^\phi$ fixed by $\phi$ is the exceptional algebra of type $\mathfrak {g}_2$. The action of that algebra on $\mathbb {R}^8$ annihilates the vector $e_0$ and the trilinear form on $e_0^\perp$

$$\begin{aligned} \omega =e^*_{1 2 6}+e^*_{13 4}+e^*_{1 5 7} +e^*_{2 3 7} + e^*_{2 4 5} +e^*_{3 5 6} +e^*_{4 67}\,, \end{aligned}$$

where $e^*_{ijk}=e^*_i\wedge e^*_j\wedge e^*_k$. This particular form defines the imaginary part of the octonionic multiplication in $\mathbb {R}^8$. Identifying $e_0$ with the unit $1\!\!1\in \mathbb {O}$ in octonions (Cayley numbers) and $e_0^\perp$ with $Im(\mathbb {O})$ we have

$$\begin{aligned} \langle a,Im(b\cdot c)\rangle =\omega (a,b,c) \end{aligned}$$

for $a,b,c\in Im(\mathbb {O})$. We note that $\omega$ has all coefficient equal to one, therefore this definition of octonionic multiplication cannot agree with the most common definition via Fano plane, see e.g. [5]. To repair the discrepancy it is enough to change the sign of the basis element $e_4$. Then the multiplication is given by the rule encoded in the picture:

Moreover $\mathfrak {so}(8)^\phi$ is the full stabilizer of $\omega$. It follows that the group of transformations of $\mathbb {R}^8$ preserving octonionic multiplication coincides with the Lie group associated to $\mathfrak {so}(8)^\phi$. There are no computations in the Cartan’s paper. We refer the readers who wish to check the formulas to [17]. A general point of view is presented and in [15, §35], but there the explicit form of $\phi$ is not given. Some forms of triality is given in [21, §24] or [23, §3.3.3].

It is a pity that this original very simple point of view on triality and the definition of the group $G_2$ as the fixed set is not wide spread in the literature. Usually there are discussed mainly the spinor representations an the nondegenerate map

$$\begin{aligned} S^+_8\times \mathbb {R}^8\rightarrow S^-_8 \end{aligned}$$

permuted by $\mathbb {Z}_3$ cyclically, [1], [10, §20.3], [15, 24]. We will construct another matrix representation of triality for $\mathfrak {so}(4,4)$ in the “Appendix”.

2 Action of triality on maximal torus

Our goal is to describe the triality in a way which does not look like a magical trick. The approach presented here is equivalent, to the Cartan’s work in the complex case. In our construction it will be clear where the formulas come from. The triality automorphism given below has an advantage, that the root spaces coincide with the coordinates of the matrix and these coordinates are permuted by $\mathbb {Z}_3$.

Working with the complex coefficients we choose a basis in $\mathbb {C}^8$ (as in [10, §19]) in which the quadratic form is equal to

$$\begin{aligned} x_1 x_8+x_2 x_7+x_3 x_6+x_4 x_5. \end{aligned}$$

For real coefficients this means that we deal with $SO(4,4)$. The maximal torus of $SO(4,4)$ consists of the diagonal matrices

$$\begin{aligned} {\textit{diag}}(e^{t_1},e^{t_2},e^{t_3},e^{t_4},e^{-t_4},e^{-t_2},e^{-t_3},e^{-t_1}). \end{aligned}$$

The following weights form the root system of $\mathfrak {so}(4,4)$:

$$\begin{aligned} \pm L_i\pm L_j\quad \text {for}\;i\not =j\,, \end{aligned}$$

where $L_i(t_1,t_2,t_3,t_4)=t_i$. Choosing the Borel subgroup as the upper triangular matrices we obtain the Dynkin diagram of simple roots:

The triality automorphism rotates the diagram anti-clockwise:

$$\begin{aligned} (L_1-L_2)\mapsto (L_3+L_4)\mapsto (L_3-L_4)\mapsto (L_1-L_2) \end{aligned}$$

and fixes the root $L_2-L_3$. In the basis consisting of the weights $L_i$ the triality automorphism is given by the remarkable matrix:

$$\begin{aligned} \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} \frac{1}{2} \;&{} \frac{1}{2} \;&{} \frac{1}{2} \;&{} -\frac{1}{2}\; \\ \\ \frac{1}{2} \;&{} \frac{1}{2} \;&{} -\frac{1}{2} \;&{} \frac{1}{2} \;\\ \\ \frac{1}{2} \;&{} -\frac{1}{2} \;&{} \frac{1}{2} \;&{} \frac{1}{2} \;\\ \\ \frac{1}{2} \;&{} -\frac{1}{2} \;&{} -\frac{1}{2} \;&{} -\frac{1}{2}\; \end{array}\right) \end{aligned}$$

(2)

3 Action on rational cohomology of $BSO (8)$

The rational cohomology ring of the classifying space of $SO(8)$ is well known, see e.g. [20, Theorem 15.9]

$$\begin{aligned} H^*(BSO(n);\mathbb {Q})=\mathbb {Q}[p_1,p_2,p_3,e]\,, \end{aligned}$$

where $p_i$’s are the Pontryagin classes and e is the Euler class of the tautological bundle. We identify the cohomology of the classifying space with the invariants of the Weyl group acting on the polynomials on $\mathfrak {t}$

$$\begin{aligned} H^*(BSO(n);\mathbb {Q})\simeq Sym^*(\mathfrak {t}^*)^W\,, \end{aligned}$$

where $\mathfrak {t}$ is the Lie algebra of the maximal torus (Cartan subalgebra), [7, Proposition 27.1]. We have

$$\begin{aligned} p_i=\sigma _i(L_1^2,L_2^2,L_3^2,L_4^2,)\quad \text {and}\quad e=L_1L_2L_3L_4\,, \end{aligned}$$

where $\sigma _i$ is the elementary symmetric function.

Theorem 1

Let $\phi$ be the triality automorphism acting on the cohomology of

$$\begin{aligned} H^*(BSO(8),\mathbb {Q})=\mathbb {Q}[p_1,p_2,p_3,e]. \end{aligned}$$

Then:

$$\begin{aligned} \phi (p_1)&= p_1\,,\\ \phi (p_2)&=-3 e + \frac{3}{8} p_1^2 - \frac{1}{2} p_2\,,\\ \phi (p_3)&= -\frac{1}{2} e\, p_1 +\frac{1}{16} p_1^3 - \frac{1}{4} p_1 p_2 + p_3 \,\\ \phi (e)&= -\frac{1}{2}e - \frac{1}{16}p_1^2 +\frac{1}{4} p_2.\end{aligned}$$

The proof is a direct computation in linear algebra. Alternatively one can ask what are the Pontryagin and Euler classes of the spin bundle $S^+$ associated to the universal principal bundle over ${\textit{BSpin}}(8)$. To know that, one has to compute the weights of the original representation and apply the corresponding $W$-symmetric function. For example the triality automorphism sends the Euler class of the standard representation to the Euler class of the spin $S^+$ representation. Its Euler class is product of weights

$$\begin{aligned} \frac{L_1\!+\!L_2\!+\!L_3\!+\!L_4}{2} \frac{L_1\!+\!L_2\!-\!L_3-L_4}{2} \frac{L_1-L_2+L_3-L_4}{2} \frac{-L_1+L_2+L_3-L_4}{2}\,, \end{aligned}$$

(3)

see [10, §20]. The result should be developed in the basis consisting of $e$, $p_1^2$ and $p_2$.

We will chose another set of generators, which is better adapted to homotopy theory. For any connected Lie group $G$ the cohomology $H^*(G;\mathbb {Q})$ is a Hopf algebra. By [18] it has to be of the form $\Lambda P^\bullet$, where $P^\bullet$ is the graded space of primitive elements of the Hopf algebra. (Dually, $H_*(G;\mathbb {Q})$ is isomorphic to the exterior power $\Lambda P_\bullet$, where the primitive spaces $P_i\subset H_i(G;\mathbb {Q})$ are images of homotopy groups.) The distinguished transgression [13, Prop. VI, p.239] of the spectral sequence

$$\begin{aligned} H^p(BG;\mathbb {Q})\otimes H^q(G)\Rightarrow H^{p+q}(EG)\,, \end{aligned}$$

identifies the primitive generators of $H^*(G;\mathbb {Q})$ with the generators of

$$\begin{aligned} H^*(BG;\mathbb {Q})\simeq Sym^*(P^\bullet [-1])\,, \end{aligned}$$

where $(P^\bullet [-1])^{i}=P^{i-1}$. The spaces $P^{i-1}\subset H^{i}(BG;\mathbb {Q})$ are preserved by automorphisms of $G$, and therefore they form a distinguished subspaces of generators. For $G=SO(8)$ or ${\textit{Spin}}(8)$ the dimensions of the spaces $P^i$ are equal to 1 for $i=3,11$ and $\dim P^7=2$. Therefore the action of the triality automorphism is nontrivial only on $P^7$. We identify the space $P^7$ with a subspace of $H^8(BSO(8);\mathbb {Q})\simeq P^7\oplus S^2 P^3$.

Proposition 1

The space $P^7$ is spanned by the Euler class $e$ and its image with respect to the triality automorphism.

The orbit of the Euler class $e$ consists of $e$ and the Euler classes of the spin representations $S^+$, $S^-$. The space spanned by them is invariant. We will show that it is of dimension two, in fact

$$\begin{aligned} e+e(S^+)+e(S^-)=0. \end{aligned}$$

Having the expression (3), and the formula for the Euler class $e(S^-)$

$$\begin{aligned} \frac{L_1+L_2+L_3-L_4}{2} \frac{L_1+L_2-L_3+L_4}{2} \frac{L_1-L_2+L_3+L_4}{2} \frac{L_1-L_2-L_3-L_4}{2}\,,\end{aligned}$$

(4)

we check directly that

$$\begin{aligned} e(S^+)=-\frac{1}{2}e - \frac{1}{16}p_1^2 + \frac{1}{4}p_2\quad \text {and} \quad e(S^-)= -\frac{1}{2}e + \frac{1}{16}p_1^2 -\frac{1}{4} p_2. \end{aligned}$$

and the result follows.

In addition it is not hard to compute that the invariant subspace of the cohomology $H^{12}(BSO(8);\mathbb {Q})$ is spanned by

$$\begin{aligned} p_1^3\quad \text { and}\quad p_3-\frac{1}{6} p_1 p_2.\end{aligned}$$

(5)

4 Cohomology with finite coefficients

For completeness we discuss now the cohomology with finite coefficients, although it will not be used in the remaining part of the paper. The cohomology of ${\textit{BSpin}}(8)$ has only 2-torsion, therefore for $q\not =2$ the cohomology $H^*({\textit{BSpin}}(8);\mathbb {F}_q)$ is generated by the same generators as for rational coefficients and the action of the triality is given by the same formula. The only special issue for $q=3$ is the fact that $H^{12}({\textit{BSpin}}(8))$ as a representation of $\mathbb {Z}_3$ is not semisimple. The invariant subspace spanned by the Euler classes $e$, $e(S^+)$ and $e(S^-)$ does not admit any invariant complement. The formula (5) does not make sense for $\mathbb {F}_3$.

The case $q=2$ is very different. The cohomology of ${\textit{BSpin}}(n)$ with coefficients in $\mathbb {F}_2$ was computed by Quillen [22, Theorem 6.5]. For $n=8$ we have

$$\begin{aligned} H^*({\textit{BSpin}}(8);\mathbb {F}_2)\simeq \mathbb {F}_2[w_2,w_3,w_4,w_5,w_6,w_7,w_8,w_8^+]/J\,, \end{aligned}$$

where $w_i$ are the Stiefel–Whitney classes of the universal bundle and $w_8^+$ is the class of the spinor bundle. The ideal $J$ is generated by $w_2$ and the results of Steenrod operation: $Sq^1(w_2)$ and $[Sq^2,Sq^1](w_2)$. In general we have

$$\begin{aligned}&Sq^1(w_2)=w_1 w_2 + w_3\,,\\&[Sq^2,Sq^1](w_2)= w_1^3 w_2 + w_1 w_2^2 + w_1^2 w_3 + w_2w_3 + w_1w_4 + w_5\end{aligned}$$

and since here $w_1=0$ we find that

$$\begin{aligned} H^*({\textit{BSpin}}(8);\mathbb {F}_2)\simeq \mathbb {F}_2[w_4,w_6,w_7,w_8,w_8^+]. \end{aligned}$$

Proposition 2

The action of the triality on $H^*({\textit{BSpin}}(8);\mathbb {F}_2)$ is the following: $\phi$ fixes $w_4$, $w_6$ and $w_7$ and

$$\begin{aligned} \phi (w_8)=w_8^+\,,\quad \phi (w_8^+)=w_8+w_8^+. \end{aligned}$$

The triality has to fix $w_4$, $w_6$ and $w_7$ since the cohomology at that gradations is one dimensional. Moreover the triality permutes cyclically the representations: the natural one, $S^+$ and $S^-$, hence $\phi (w_8^+)=w_8(S^-)$. It remains to show that $w_8(S^-)=w_8+w_8^+$. By Proposition 1 we have

$$\begin{aligned} e+e(S^+)+e(S^-)=0\end{aligned}$$

(6)

in rational cohomology. The group $H^8({\textit{BSpin}}(8);\mathbb {F}_2)$ is spanned by $w_8$, $w_8^+$ and $w_4^2$. The top Stiefel–Whitney classes are the reductions modulo 2 of the integral Euler classes $e$, $e(S^+)$ and $e(S^-)$. Also the class $w_4$ is the reduction modulo 2 of the integral Pontryagin class $p_1$. Therefore the relation (6) has to hold also in $\mathbb {F}_2$ cohomology.

We will not discuss here the cohomology with integral coefficients, their generators are to be found in [6].

5 Triality of the singularity $D_4$

Triality phenomenon seem to attract recently mathematicians working on singularity theory. In a preprint [14] the triality was related to the study of integral curves. We will discuss here only very basic and obvious appearance of triality in singularities of scalar functions. The simple singularities of germs of holomorphic functions $\mathbb {C}^n\rightarrow \mathbb {C}$ are indexed by the Dynkin diagrams $A_\mu$ for $\mu \ge 1$, $D_\mu$ for $\mu \ge 4$, $E_6$, $E_7$ and $E_8$. The Dynkin diagram $D_4$ describes the intersection form in the homology of the Milnor fiber in the distinguished basis corresponding to the basic vanishing cycles (defined by a choice of paths joining the singular values of a morsification with a regular one as in [4, Ch. 2] or [25, §4]).

The singularity $D_4$ is given by the formula

$$\begin{aligned} f:\mathbb {C}^2\rightarrow \mathbb {C}\,,\qquad f(x,y)=x^3-3xy^2=x\,(x-\sqrt{3}\, y)\,(x+\sqrt{3}\, y). \end{aligned}$$

We have chosen the real form $D_4^-$ since the triality does not act on the real form $D_4^+$ defined by $x^3+3xy^2$. We will observe how triality acts on the spaces related to that singularity. The link of the singularity consists of three circle in $S^3$ linked with each other. They bound a surface, which is homeomorphic to the Milnor fiber:

The link and the Milnor fibre ¹ contained in $S^3$

The real part of the zero set of the function $f$ is the union of three lines intersecting at the angle 120$^{\circ }$. The rotation of the $(x,y)$ plane by that angle preserves the function. Denote this rotation by $\phi _0$. The map $\phi _0$ of $\mathbb {R}^2$ (or $\mathbb {C}^2$) is determined by the angles at which the lines intersect (up to a cubic root of unity in the complex case). We remark, that if one takes $x^3-xy^2$ as the germ representing the singularity, then the formula for $\phi _0$ and $\phi$ does not involve irrational coefficients like $\cos (120^{\circ })$ and $\sin (120^{\circ })$.

The Milnor fiber $M_\varepsilon$ for $\varepsilon <<1$ is described by the equation

$$\begin{aligned} x^3-3xy^2=\varepsilon \,,\quad |x|^2+|y|^2\le 1. \end{aligned}$$

It is an elliptic curve with three discs removed. We can forget the inequality (since $f$ is homogeneous) and we identify the Milnor fibre with the plane cubic curve. The automorphism $\phi _0$ preserves $M_\varepsilon$ permuting cyclically the removed discs.

Let

$$\begin{aligned} F:\mathbb {C}^2\times S\rightarrow \mathbb {C}\end{aligned}$$

be a miniversal deformation of $f$, (see [3, §8], for the definition). Here $S$, the parameter space of the deformation, is of dimension $\mu =4$. It can be naturally identified with $H_1(M_\epsilon ,\mathbb {C})/W$, where $W$ is the Weyl The group $W$ is generated by the reflections in the basic vanishing cycles corresponding to the singular points of a morsification of $f$. The map $H_1(M_f,\mathbb {C})/W\rightarrow \mathbb {C}^4$ is given by the period map constructed in [16, Theorem 1.2], [4, Ch.2 §3]. Let us see how the described construction can be done equivariantly with respect to the triality.

First let us find a deformation which is invariant with respect to the rotation $\phi _0$.

Proposition 3

The function

$$\begin{aligned} F(x,y,a,b,c,d)=x^3-3xy^2+a(x^2+y^2)+\langle (b,c),(x,y)\rangle +d \end{aligned}$$

is a miniversal deformation of $f(x,y)=x^3-3xy^2$. It is invariant with respect to triality, provided that the action on the parameter space is given by

$$\begin{aligned} \phi (a,b,c,d)=(a,\phi _0(b,c),d). \end{aligned}$$

The function $F$ is clearly invariant since $\phi _0$ preserves the scalar product $\langle (b,c),(x,y)\rangle$. The choice of the quadratic term is forced by the invariance condition. The functions $1$, $x$, $y$ and $x^2+y^2$ form a basis of the local algebra $\mathbb {C}[x,y]/(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$, as desired in the definition of miniversal deformation.

Let us take a $\phi$-invariant morsifications of $f$

$$\begin{aligned} f_a(x,y)=x^3-3xy^2+3a(x^2+y^2)-4a^3=(x-a)( x - \sqrt{3} y+2a) ( x - \sqrt{3} y+2a). \end{aligned}$$

(7)

We easily compute that $f_a$ has the critical points at

$$\begin{aligned} p_Y=(0, 0)\,,\; p_A= (-2 a, 0)\,,\;p_B=( a , -{a}{\sqrt{3}})\,,\;p_C= (a , {a}{\sqrt{3}}). \end{aligned}$$

The first critical value is $-{4 a^3}$ (minimum), the remaining three values are equal to 0 (saddle points). It follows that the vanishing cycles associated to $p_A$, $p_B$ and $p_C$ are perpendicular (see [25, §4, Theorem 4.26]) they correspond to the roots $A$, $B$ and $C$. The map $\phi _0$ rotates them cyclically. Therefore $\phi _0$ realizes the triality automorphism of the root system $D_4$. Topologically the system of vanishing cycles is homeomorphic to the following configuration:

Note that the action of $\phi$ coincides with the action on the distinguished generators of $H^*({\textit{BSpin}}(8);\mathbb {R})$ found in Proposition 1. The singularity $D_4$ is homogeneous, and the coefficients of the miniversal deformation can be given the gradations

$$\begin{aligned} \deg (a)=1,\quad \deg (b)=\deg (c)=2,\quad \deg (d)=3\,, \end{aligned}$$

so that the whole function $F$ is quasihomogeneous. We obtain

Theorem 2

Let $a,b,c,d$ be the coefficients of the miniversal deformation of the singularity $D_4^-$. There exists an isomorphism

$$\begin{aligned} H^*(BSO(8),\mathbb {R})\simeq \mathbb {R}[a,b,c,d]\,, \end{aligned}$$

which preserves the action of the triality automorphism and agrees with the gradation after dividing by 4 the degrees in $H^*(BSO(8),\mathbb {R})$.

If fact this isomorphism is the composition of the isomorphisms

$$\begin{aligned} H^*(BSO(8),\mathbb {R})\simeq Sym^*(\mathfrak {t}^*)^W\simeq Sym^*(H^1(M_\epsilon ))^W\simeq \mathbb {C}[H_1(M_\epsilon )/W] \end{aligned}$$

and the period mapping. The last step is the most involving since according to the assumption of [16, Theorem 1.2] demands enlarging the dimension of the domain of $f$. We just settle for an abstract isomorphism.

The bifurcation set of the singularity $D_4^-$ is defined by

$$\begin{aligned} \{(a,b,c)\in \mathbb {R}^3\;|\;\exists \,(x, y)\in \mathbb {R}^2 \;grad(F)(x,y)=0, \;Hessian(F)(x,y)=0\} \end{aligned}$$

in the reduced parameter space $d=0$. (Here $F$ is the miniversal deformation of $f$ defined in Proposition 3.) It has clearly a $\mathbb {Z}_3$ symmetry.

6 Singularity $G_2$?

The Dynkin diagram $G_2$ does not appear in the original Arnold’s classification of simple singularities as well as the series $B_\mu$, $C_\mu$ and the exceptional $F_4$. The other diagrams appear in [2] (see also references in [12]), while $G_2$ is only mentioned in remark at the end of §$9$. The series $B_\mu$ and $C_\mu$ arise as diagrams for the singularities with boundary condition. We will show how the diagram $G_2$ appears for singularities with $\mathbb {Z}_3$ symmetry.

It is worth to continue the analogy with the world of Lie algebras. Here the situation is dual, instead of taking the fixed points we divide by the $\mathbb {Z}/3$ action. The function $f$ factors to the quotient $\bar{f}: \mathbb {C}^2/\mathbb {Z}_3\rightarrow \mathbb {C}$. The quotient space is not smooth, but it has mild singularities, an isolated du Val singularity of the type $A_2$. The new Milnor fiber $\overline{M}_\varepsilon$ is the quotient of the original Milnor fiber $M_\varepsilon$. The quotient map is an unbranched cover. Therefore the $\overline{M}_\varepsilon$ is homeomorphic to an elliptic curve with one disc removed. The cohomology $H^1(\overline{M}_\varepsilon ;\mathbb {Q})$ is generated by two vanishing cycles corresponding to the singular values of the invariant morsification (7). The vanishing cycle corresponding to the value $0$ is the usual one. The value $-4 a^3$ corresponds to the vanishing cycle shrieked to the singular point of the domain. It is reasonable to treat the quotient space as $\mathbb {C}^2/\mathbb {Z}_3$ as a stack. Here it simply means that we consider the singularity $D_4$ together with the $\mathbb {Z}_3$-symmetry, as it was done in [11] for unitary reflection groups. We compute the intersection number of a pair of cycles taking their inverse images in the cover and dividing the result by the order of the cover.

To see what is the associated diagram of that singularity we pass to an odd dimension, adding a nondegenerate quadratic form, e.g.

$$\begin{aligned} \Sigma {f}(x,y,z)=x^3-3xy^2+z^2. \end{aligned}$$

Then the self-intersection of the cycle corresponding to $[p_A]$ is $-2$, and the self intersection of the cycle corresponding to $[p_Y]$ is equal to $-\frac{2}{3}$. The intersection diagram is exactly $G_2$:

$$\begin{aligned} _{[p_A]=[p_B]=[p_C]}\;\bigcirc \equiv \!\!\!\equiv \!\!\!\equiv \!\!\!\!\big >\!\!\!\equiv \!\!\!\equiv \bigcirc \;_{[p_Y]}. \end{aligned}$$

We will give more precise description of the Milnor fiber of $\bar{f}$. It is contained in the quotient space $\mathbb {C}^2/\mathbb {Z}_3$ which has the ring of algebraic functions isomorphic to

$$\begin{aligned} \mathbb {C}[u,v,w]/(u^2+v^2-w^3)\,, \end{aligned}$$

by setting $u=x^3-3x y^2$, $v=y^3 -3 x^2 y$ and $w=x^2+y^2$. The function $\bar{f}$ is equal to $u$. We see that $\overline{M}_\epsilon$ is described in $\mathbb {C}^3$ by the equations

$$\begin{aligned} \left\{ \begin{matrix} u^2+v^2=w^3\\ u=\varepsilon . \end{matrix}\right. \end{aligned}$$

Hence it is isomorphic to the plane cubic

$$\begin{aligned} v^2=w^3-\varepsilon ^2. \end{aligned}$$

All the fibers are isomorphic as algebraic curves. Topologically, the classical Milnor fibration

$$\begin{aligned} {\textit{arg}}(f):S^3{\setminus } f^{-1}(0)\rightarrow S^1 \end{aligned}$$

descends to a fibration from the complement of a circle in the lens space

$$\begin{aligned} {\textit{arg}}(\bar{f}):L(3;1){\setminus } S^1\rightarrow S^1 \end{aligned}$$

with the fiber homeomorphic to the topological 2-torus with one point removed.

Let $g(s,t)=s^3-t^2$ be a germ of $A_2$ singularity. Note that we have a commutative diagram

Therefore the germ of $\bar{f}$ is induced from $g$ by a double covering of $\mathbb {C}$. It is not coincidence. The root system of the Lie algebra $\mathfrak {g}_2$ contains the root system of the algebra of the type $A_2$.

The miniversal deformation of $G_2$ germ is understood as a slice in the space of jets of invariant function, which is transverse to the orbit of the function $f$. It is clearly equal to

$$\begin{aligned} F[x,y,a,0,0,d]=u+a\, w+d. \end{aligned}$$

The associated family of fibers

$$\begin{aligned} \left\{ \begin{matrix}u^2+v^2=w^3\\ u+a\,w+d=0.\end{matrix}\right. \end{aligned}$$

is a nontrivial family of plane cubic curves

$$\begin{aligned} v^2=w^3-(a\,w+d)^2. \end{aligned}$$

We conclude with the remark that an analogous construction can be applied to the singularity of $n$ lines intersecting at one point

$$\begin{aligned} f(x,y)=\prod _{k=1}^n(\cos ({k\pi }/n) x+\sin ({k\pi }/n)y ), \end{aligned}$$

which is symmetric with respect to the group $\mathbb {Z}_n$ acting by the rotations with the angles $\frac{2k\pi }{n}$. The resulting quotient Milnor fiber is isomorphic to a complex curve of genus $\frac{n-1}{2}$ with one disc removed, when $n$ is odd. For $n$ even the quotient Milnor fiber is a complex curve of genus $\frac{n-2}{2}$ with two discs removed. That construction for $n>3$ seem not to have a counterpart in the realm of Lie algebras.

Appendix

1.1 Triality in $\mathfrak {so}(4,4)$

In Sect. 2 we have given a formula for triality automorphism acting on the dual $\mathfrak {t}^*$ of the Cartan subalgebra of $\mathfrak {so}(4,4)$. It does not preserve the lattice corresponding to the group $SO(4,4)$ but it preserves the lattice spanned by $L_i$’s and $\frac{1}{2}(L_1+L_2+L_3+L_4)$, which corresponds to ${\textit{Spin}}(4,4)$, the cover of $SO(4,4)$. We list below the set of positive roots:

The boxed roots are fixed by triality. It can be easily seen when we express the roots in the basis of simple roots:

Here for example $ABC2Y$ denotes the root $A+B+C+2Y$. Dividing roots into orbits of the triality automorphism we see that we have the fixed roots $Y$, $ABCY$ and $ABC2Y$. Three free orbits are generated by $A$, $AY$ and $ABY$.

From general theory it follows that the triality automorphism of weights lifts to a self-map of the Lie algebra $\mathfrak {so}(4,4)$. But a priori it is not clear that one can find such a lift of order three. Not every lift satisfies $\phi \circ \phi \circ \phi =Id$. The choice of signs is not obvious and demands a careful check. All the calculations can be found in [17]. The elements of $\mathfrak {so}(4,4)$ for our quadratic form defined by the matrix with 1’s on the antidiagonal are the matrices $\left( m_{ij}\right) _{1\le i,j\le 8}$ which are antisymmetric with respect to the reflection in the antidiagonal. Such a matrix is transformed by the triality automorphism to the following one

The upper half of the diagonal $(t_1,t_2,t_3,t_4)=(m_{11},m_{22},m_{33},m_{44})$ is transformed by the matrix (2) to

$$\begin{aligned} \frac{1}{2} (m_{11} + m_{22} + m_{33} -&m_{44})\\ \frac{1}{2} (m_{11} + m_{22} -&m_{33} + m_{44})\\ \frac{1}{2} (m_{11} -&m_{22} + m_{33} + m_{44})\\ \frac{1}{2} (&m_{11} - m_{22} - m_{33} - m_{44}) \end{aligned}$$

We remark that this is an unique automorphism with real coefficients extending the self-map of the maximal torus. We would like to stress, that both: the Cartan construction of triality for $\mathfrak {so}(8)$ and the triality for $\mathfrak {so}(4,4)$ presented here works for any ring in which 2 is invertible. On the other hand we note that the remaining real forms of the orthogonal algebra $\mathfrak {so}(k,k-8)$ for $k=1,2,3,5,6,7$ do not admit any triality automorphism with real coefficients. Already on the level of $\mathfrak {t}^*$ we obtain the rotation matrices with imaginary coefficients.

1.2 Noncompact version of $G_2$

The algebra fixed by $\phi$ consist of matrices of the form

Below we formulate a fundamental fact (known to the specialists) to which we could not find a reference except the paper of [9] for $\mathfrak {so}(8)$ form or without a explicit matrix realization in [21, §24], [23, §3.3.3], [15, Prop 35.9].

Theorem 3

The fixed points of the triality automorphism is a Lie algebra of the type $\mathfrak {g}_2$.

Indeed, the fixed elements of $\mathfrak {t}^*$ is spanned by the simple roots $Y=L_2-L_3$ (the longer root) and $\frac{1}{3}(A+B+C)=\frac{1}{3}(L_1-L_2+2L_3)$ (the shorter root)

$$\begin{aligned} _{\frac{1}{3}(A+B+C)}\;\bigcirc \equiv \!\!\!\equiv \!\!\!\equiv \!\!\!\!\big <\!\!\!\equiv \!\!\!\equiv \bigcirc \;_Y. \end{aligned}$$

The shorter root as the functional on $\mathfrak {t}^\phi$ is equal to $A$ or $B$ or $C$, but we represent it as an invariant element $\frac{1}{3}(A+B+C)\in (\mathfrak {t}^*)^\phi$. The positive root spaces of $\mathfrak {so}(4,4)^\phi$ are the following:

• the eigenspaces associated to the longer roots

  $$\begin{aligned} \mathfrak {so}(4,4)_{ Y},\quad \mathfrak {so}(4,4)_{ ABCY},\quad \mathfrak {so}(4,4)_{ ABC2Y} \end{aligned}$$

• the diagonal subspaces associated to the shorter roots $\frac{1}{3}(A+B+C)$, $\frac{1}{3}(AY+BY+CY)$, $\frac{1}{3}(ABY+ACY+BCY)$

  $$\begin{aligned}&\big (\mathfrak {so}(4,4)_{ A}\oplus \mathfrak {so}(4,4)_{ B}\oplus \mathfrak {so}(4,4)_{ C}\big )^\phi \\&\big (\mathfrak {so}(4,4)_{ AY}\oplus \mathfrak {so}(4,4)_{ BY}\oplus \mathfrak {so}(4,4)_{ CY}\big )^\phi ,\\&\big (\mathfrak {so}(4,4)_{ ABY}\oplus \mathfrak {so}(4,4)_{ ACY}\oplus \mathfrak {so}(4,4)_{ BCY}\big )^\phi . \end{aligned}$$

1.3 The twin-brother of octonion algebra

We repeat the construction of the $\mathfrak {g}_2$ algebra and the octonions from Sect. 1. The Lie group corresponding to $\mathfrak {so}(4,4)^\phi$ is the noncompact form of $G_2$ since its maximal torus is $(\mathbb {R}^*)^2$. The Lie algebra $\mathfrak {so}(4,4)^\phi$ annihilates the vector $v_0=e_4-e_5$ and its action restricted to $v_0^\perp$ preserves the form

$$\begin{aligned} \widetilde{\omega }=2e^*_{1 6 7} + 2 e^*_{2 3 8} + e^*_{2 (4+5) 7}-e^*_{1 (4+5) 8} + e^*_{3 (4+5) 6} \,, \end{aligned}$$

where $e^*_{i(4+5)j}$ means $e^*_i\wedge (e^*_4+e^*_5)\wedge e^*_j$. The associated algebra is the algebra of pseudo-Cayley numbers (also called split octonions). The form $\widetilde{\omega }$ is of the type 5 according to the classification of real multisymplectic forms in dimension 7 in [8].