1 Introduction

Random numbers [1, 2] have been considered as important for research works varying from Computer Science to Mathematics. It is reported that the values of random numbers are homogeneously distributed over a well defined interval and it is unfeasible to predict the next values for a random pattern.

‘Seed’ has been used as a specification of an initial number for generation of a random pattern. Random number generators (RNGs) are classified into several groups based on the difference in generation procedures of random numbers. Pseudo-random number and true-random number are most commonly used in scientific works. Classification of RNGs is entirely based upon the selection method for ‘seed’.

Random numbers or random-patterns [1, 2] obtained with an execution of a computer program is based on a particular recursive algorithm. Deterministic way for selection of ‘seed’ has referred the pattern generation procedure as ‘Pseudo’ [3].

Sophisticated method of generating high quality pseudo-random numbers has been established with the uses of CA [4]. CA is a dynamic mathematical model to represent the dynamic behavior of any system. A typical structure of 3-cell null boundary CA is represented in Fig. 1.

Fig. 1
figure 1

Typical structure of 3-cell null boundary CA

Full size image

Quality of randomness generated by a RNG is verified with Diehard tests. Diehard statistical test suit has been developed by George Marsaglia [5].

Rest of the paper is organized as follows: related works are described in Sect. 2; background has been described in Sect. 3; proposed work is presented in Sect. 4; Experimental observations and result analysis are shown in Sect. 5 and Conclusion is presented in Sect. 6.

2 Related works

Research works have been established to generate good quality random numbers [3, 4, 6]. Important efforts have also been established to generate pseudo-random numbers using CA [7–13]. It has been already established that the maximum degree of randomness is found in maximum length cellular automata (MaxCA) based PRNG [3, 6–9].

Random patterns are achieved based on the following recursive Eq. 1.

$$ X_{n + 1} = P_{1} X_{n} + P_{2} \left( {\bmod \,N} \right) $$
(1)

Here ‘P1’, ‘P2’ are prime numbers; ‘N’ is range for random numbers; ‘Xn’ is calculated recursively using the base value ‘X0’; ‘X0’ is termed as seed and it is a prime number; if ‘X0’ (seed) is same all time or selected in any deterministic way, then it yields pseudo-random number [1].

CA has been successfully used as a PRNG. It is reported that with the increased number of cells, maximum amount of randomness is found in resulting maximum length cycle. In MaxCA, prohibited pattern set (PPS) is excluded from the cycle. It has been observed that in the generation process of pseudo-random pattern using MaxCA, only a large cycle is responsible for yielding the pseudo random patterns.

Dissimilar degrees of randomness in their generated patterns are found for different PRNGs. Besides there exist some real issues to select one of them as a cost effective RNG. The recursive algorithm based RNG is much more deterministic in the process of ‘seed’ selection. In MaxCA, the generation procedure of PPS free random pattern is complex. In this methodology, it is mandatory to keep track of PPS in maximum length cycle and to exclude this portion in resulting maximum length cycle [7–14]. The associated cost should be increased for generation of pseudo-random patterns using a single cycle with larger numbers of states. All the cost associated with the generation process of random numbers; i.e., time, design and searching costs are having higher values as the complexity is directly proportional to the number of states used in CA generated cycle(s). So, it is convenient to reduce the cycle length without affecting the randomness quality of the generated random patterns for reducing these associated costs. Therefore, an alternative easy to implement generation methodology of random numbers would be much more beneficial which will optimize these types of flaws. In our proposed methodology, we have proposed a system that will be dealing with the flaws of the MaxCA but still is capable to generate patterns that are having the same quality of randomness as compared to MaxCA. Thus the proposed methodology should be more cost effective in terms of design complexity, time complexity and searching complexity [15–17]. The detailed discussion of the proposed methodology is following Sect. 4.

3 Background

A cost effective random sampling process with CA, has been introduced for Digital Forensic investigations [18]. Equal length cellular automata (ELCA) based pseudo-random pattern generator (PRPG) has been proposed in a cost effective manner utilizing the concept of random pattern generation. Exhibition of high degree randomness has been demonstrated in the field of randomness quality testing. Comparative studies among different RNGs have also been included to demonstrate the effectiveness of proposed ELCA PRNG. Some well known random number generators, e.g., recursive pseudo-random number generator (RPRNG), atmospheric noise based true-random number generator (TRNG), Monte-Carlo (MC) pseudo-random number generator and MaxCA random number generator random number generator have been compared here with proposed ELCA.

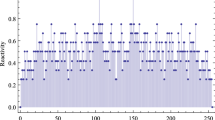
A small data set generated by these different RNGs has been collected to visualize the randomness quality of the corresponding RNGs. The randomness quality graph is followed in Fig. 2.

Fig. 2
figure 2

Randomness quality graph for five different RNGs

Full size image

Results obtained in Diehard tests for different RNGs have been further reported in Fig. 3.

Fig. 3
figure 3

Diehard performance graph

Full size image

Different degree of randomness of the corresponding RNGs for a small data set is presented in Fig. 3. It is found from Fig. 3 that the Recursive PRNG is having the least degree of randomness where as MaxCA PRNG and ELCA PRNG shares almost equal degree of randomness among themselves and both of them are having the maximum degree of randomness compared to all other RNGs.

In practice, MaxCA based random number generator produces the random pattern of integer using the cycle which might contain some of the restricted configurations. In this scenario, the PPS is excluded form that MaxCA cycle. Assume that there exist some an n-numbers of prohibited patterns in maximum length cycle. Let the PPS is {RC0,…, RCn}. For the exclusion purpose of these patterns from concerned cycle, the minimum length of arc (Arcmin) between the prohibited pattern RC0 and RCn should be measured so that we utilize the remaining cycle arc i.e., effective arc (Earc) for random number generation, which is typically free from PPS. This scenario is described in Fig. 4 [19].

Fig. 4
figure 4

Typical cycle structure to deal with the problem of PPS

Full size image

Figure 4 is based on the facts that there exists total n-number of restricted configurations with the following set: PPS = {RC0,…..,RCn}. The procedure to measure Arcmin and Earc is described in Fig. 4 [19].

Definition 1

The minimum length of arc (Arcmin) is the minimum distance between the first and last prohibited pattern in an n-cell MaxCA cycle [19].

Definition 2

The effective arc (Earc) is the remaining arc length of an n-cell MaxCA cycle which excludes Arcmin from the corresponding CA cycle of states and it is responsible for generating pseudo random patterns of integers [19].

Resulting sequences for all those above mentioned pattern generators have significant improvement in terms of randomness quality. Emphasis on cost effectiveness generation of pseudo-random pattern has further been focused in Sect. 4.

4 Proposed work

Cost effective and simpler design methodology for the generation of random integer patterns has been reported here. The cost efficiency in proposed PRNG refers to the space, time, searching and design complexity for any involved algorithm. In the cost optimization generation methodology for universal pseudo-random pattern, ELCA has been proposed over the existing MaxCA random pattern generator.

In the proposed methodology, ELCA based approach has been proposed to achieve high degree of randomization in terms of better cost optimization with respect to all the concerning complexities mentioned earlier. Projected methodology is very much convenient for hardware implementation. The quality of randomness of the generated pattern by proposed methodology is compared through Diehard test with some other recognized RNGs. The conclusion is made about the quality of randomness of any data set based on the number of Diehard test passed.

In our work, instead of opting for MaxCA, we propose for decomposition of an n-cell CA into more relevant sub-cycles such that our concerning complexities cost are reduced as well as the fault coverage is more flexible than of previously established MaxCA. The proposed PRNG system design is described in Fig. 5.

Fig. 5
figure 5

Flowchart of proposed ELCA based random pattern generating system

Full size image

A mathematical approach has been proposed to achieve the same amount of randomization in less cost with respect to various complexities and hardware implementation, according to the flowchart of the proposed system as mentioned in Fig. 5.

The resulting ELCAs are capable of generating random patterns as equivalent to the randomness quality achieved from MaxCA. The following Algorithm 1 [15, 16] has been used for decomposition of an n-cell CA.

Algorithm 1:

PPS_Free_ELCA_Generation

Input: CA size (n), PPS Set

Output: m-length ELCAs excluding PPS

Step 1: Start

Step 2: Initialize the number of n-cell CA to generate random patterns using n-cell CA

Step 3: Initialize balanced CA rule to all the cells for generation of ELCA

Step 4: Decompose the cell number (n) into equal numbers (m) such that 2 m *(2 n − m ) (i.e., ‘m’ number of ELCA) for n ≥ 1 and m = 1,2,3…… (n − 1)

Step 5: Check each prohibited pattern whether belongs to a single smaller cycle CA or not

Step 6: Repeat Step 3 and Step 4 until each prohibited pattern belongs to some ELCAs

Step 7: Allow m-length cycles of n-cell CA after excluding all the PPS containing ELCA

Step 8: Stop

In proposed methodology, our primary concern is to exclude PPS. Prohibited pattern implies a bit configuration for which any circuit shows non-computability. Therefore it has been taken care of that the occurrence of every prohibited pattern must be enclosed in some of the smaller sub-cycles, such that by eliminating all those smaller cycles, the remaining cycles are allowed to generate random patterns. Thus, this methodology implies a better-cost effectiveness approach. Our proposed methodology thus simplifies design complexity and empowers the searching complexity. The terminology design complexity refers to implementation procedure for generation of random pattern and empowering searching complexity means zero overheads for keeping track for PPS in random pattern generation. In comparison with n-cell MaxCA, more number of smaller cycles instead of one maximum length cycle should be used.

In contrast with an n-cell MaxCA, ELCA has been introduced as an alternative PRNG. Consider, CA size = n;

$$ \begin{aligned} {\text{Then}}, \, 2^{\text{n}} & = \, 2^{\text{n - 1}} + 2^{\text{n - 1}} \\ & = 2*(2^{\text{n - 1}} ) \, \left( {{\text{i}} . {\text{e}} . , {\text{ two number of equal length cycles}}} \right) \\ & = \, 4*(2^{\text{n - 2}} ) \\ & = \, 2^{2} *(2^{\text{n - 2}} ) \, \left( {{\text{i}} . {\text{e}} . , {\text{ four number of equal length cycles}}} \right) \\ & = \, 2^{\text{m}} *\left( {2^{{{\text{n}} - {\text{m}}}} } \right) \, ({\text{i}} . {\text{e}} . , { }2^{\text{m}} {\text{number of equal length cycles}}){\text{ for n}} \ge 1 \, \\ & {\text{and m}} = 1, \, 2, \, 3 \ldots \ldots . \, \left( {{\text{n}} - 1} \right) \\ {\text{So we have }}2^{\text{n}} & = 2^{\text{m}} * 2^{{({\text{n}} - {\text{m}})}} \ldots \\ \end{aligned} $$
(2)

Thus ‘m’ is always less than ‘n’ [19].

Example 1

Consider a case where CA size’n’ is 5.

So, 25 = 22*2(5 − 2) = 4*24 (i.e., total four numbers of equal length cycles of size eight), or = 23*2(5 − 3) = 8*22 (i.e., total eight numbers of equal length cycles of size four).

Consider that there exist five numbers of prohibited patterns. In our proposed design methodology, in worst case all prohibited patterns are in five different cycles. So, remaining 8 − 5 = 3 cycles are allowed to generate pseudo-random patterns.

Each prohibited pattern is excluded from the cycle as per the procedure for generating random patterns in MaxCA. In our procedure, PPS are totally removed as we are having more number of cycles for generation of random sequences. In proposed methodology, the cycles containing prohibited patterns are removed completely from the generation of pseudo random numbers.

Example 2

An n-cell CA for n = 5 might be decomposed into some equal length smaller cycles instead of one maximum length cycle. In our illustrated example it is decomposed into four smaller cycles of length 8 (Refer Fig. 6b); or, it is decomposed into eight smaller cycles of length 4 (Refer Fig. 6c). Pattern generation in this scenario is followed as referred in Fig. 6. Maximum length cycle is shown in Fig. 6a; Fig. 6a is based on null boundary 5 cell CA having rules in specified sequence <90, 90, 90, 90, 150>. The synthesis of this example in Fig. 6b, c ELCA are achieved for a combination of balanced CA rules such as “60”, “102”, “153”, “195” for CA size n = 5.

Fig. 6
figure 6

a MaxCA Cycle for n = 5 for <90, 90, 90, 90,150>. b Proposed 4 ELCA of cycle size 8 for <153,153,153,153,153>. c Proposed 8 ELCA of cycle size 4 for <60, 60,195,102,153>

Full size image

Characteristics of CA rules for generating ELCA has revealed the fact that all CA rules are balanced in nature and initiate a pair of necessary and sufficient conditions as reported below:

Necessary Condition for ELCA Higher bits partition (HbP) and lower bits partition (LbP) in binary representation for the CA rule, is balanced, i.e., HbP and LbP both individually contains two numbers of 0’s and two numbers of 1’s.

Sufficient Condition for ELCA 8 bit binary representation for the CA rule, is balanced, i.e., the binary representation contains four numbers of 0’s and four numbers of 1’s.

Upon illustration of the above stated conditions, let consider a balanced rule “51”. Rule “51” are represented in 8 bit binary format as presented in Fig. 7. Binary representation for rule “51” is shown in Fig. 7. Here HbP (Higher bits partition) and LbP (lower bits partition) section show that they are individually balanced and rule “51” itself is balanced.

Fig. 7
figure 7

Binary representation of rule “51”

Full size image

In our research, we have found that CA rules for ELCA generation procedure are balanced in nature. The set of balanced CA rules for generation of ELCA as discussed in earlier example, are: “51”, “60”, “102”, “153”, “195” and “204”. A study of these rules reveals following information as presented in Table 1. Combinatorial logic of Table 1 has been visualized with reference to Fig. 1. Here current state is denoted by ‘(t)’ and next state is denoted by ‘(t + 1)’. Information of the CA rules for ELCA generation procedure is presented in Table 1.

Table 1 ELCA rule information
Full size table

Corollary 1

All the balanced CA rules, whose HbP and LbP positions are not balanced, are not responsible for generating ELCA.

Proof

From the binary equivalent of thse CA rule as reported in Table 1, it is found that all the rules are having equal numbers of 0’s and 1’s. in its HbP and LbP position. There exist a total two numbers of 0’s and two numbers of 1’s in binary format at HbP and LbP positions for every rule. That indicates that all the rules are balanced at their HbP and LbP position. So an unbalanced situation at HbP and LbP position never satisfy the necessity and sufficiency conditions. Hence no rule with unbalanced condition at HbP and LbP position is bound to generate ELCA.□

Theorem 1

Space complexity is at least same for proposed methodology with respect to MaxCA.

Proof

Space complexity increases with the increased number of cells in a CA. Increased numbers of CA cells require more hardware component for implementation.

The space complexity for a p-cell MaxCA is O (n) ∀ n = 2p

The space complexity for ELCA is O (m).

From Eq. 2 we have 2n = 2 m*(2n−m). That is the same number of CA states are generated in ELCA. Hence ∑O (mi) = O (n) in case of space complexities. Here “i” denote number of equal length cycle that has been decomposed from a MaxCA using Eq. 2.

That is the memory space to process a fixed length of an n-cell CA is always same.□

Consider that there exists 5 numbers of prohibited patterns in an n-cell CA. Now to generate random patterns, MaxCA methodology needs to calculate Arcmin and Earc. For our proposed methodology, in worst case all of the PPS will fall into five different ELCA. So in worst case scenario, there should remain (8 − 5 = 3) number of ELCA of size 4, those are PPS free ELCA for generating random patterns.

Theorem 2

Design cost of proposed system is less than MaxCA.

Proof

Proposed methodology is allowed only to generate random patterns from smaller cycles that do not contain PPS. The PPS exclusion feature from the main cycle, which is responsible for generating random patterns, improves the design complexities. The logic behind this simplicity is that the proposed methodology simply discards the equal length cycles contains prohibited patterns. So there is no need to keep track of Arcmin length in the cycle. Concept of Arcmin and Earc is only applicable for MaxCA based design only.

For MaxCA, let the time taken for calculating Arcmin and Earc are Tarc and TE respectively. So the pattern generation time is T = Tarc + TE. For ELCA, there is no concept of calculating Tarc and TE. All the PPS containing smaller cycles are discarded from pattern generation process. So the time taken for pattern generation TELCA is equal to execution time for remaining prohibited patterns free smaller length cycle only. Thus TELCA is free from the overhead of calculation of Tarc and TE. Hence its design complexity is simpler compared to MaxCA.

Hence the assumption is true. □

Theorem 3

Time complexity is less in proposed methodology with respect to MaxCA.

Proof

In the proposed methodology random pattern is only allowed to generate from equal length CA which are smaller in size. Furthermore those equal length cycles are free of PPS. So execution times for those smaller cycles are much less with respect to MaxCA. The time complexity of an n-length CA is O (n). But in our proposed methodology, the MaxCA is decomposed into several smaller equal length cycles, which results the decrease of time complexity into O (m). It is earlier described in Eq. 2. Here this “m” is smaller than “n”. Hence the time complexity of equal length is less than the time complexity of MaxCA.

The time complexity of MaxCA is O (n) ∀ n = 2p for a p-cell CA.

The time complexity of ELCA is O (m) ∀ m = 2q for a q-cell CA

From Eq. 2, we have m < n, thus we have, O (m) < O (n).

Hence the time complexity of ELCA is lesser with respect to MaxCA. □

Theorem 4

Proposed methodology is at least equal to the maximum length scheme in quality of randomness.

Proof

The quality of randomness in an n-length CA increases with the number of cell (n). More the number of states in a cycle, better the quality of randomness in generated patterns are achieved, as there exist lesser chances of repetition of the generated pattern. High numbers of states are available with higher numbers of “n” to reduce the chances of any possible repetition. This is truly presented in the Diehard test result in Table 4. It has also been reported in Table 4 that MaxCA and proposed methodology are having the same degree of randomness. Both of mechanism have scored a total number of 10 and 14 respective Diehard test passes for CA size n = 23 and 64 respectively. Hence the assumption is true. □

5 Experimental observations & result analysis

PPS containing arc in random pattern generating cycle is excluded from the cycle as per the procedure for generating the maximum random pattern in MaxCA (Refer Fig. 4). On the other hand, the PPS containing cycles are totally removed to generate the random sequences. There is no overhead to calculate Earc and Arcmin in proposed ELCA methodology. Table 2 compares the procedures of MaxCA (Refer Fig. 8a) and ELCA based random pattern generators.

Table 2 Comparison of fault coverage procedures
Full size table
Fig. 8
figure 8

a MaxCA cycle structure with PPS. b ELCA cycle structure with PPS

Full size image

Figure 8 is based on an arbitrarily drawn scenario where total number of prohibited patterns is 5 and let an arbitrary PPS is {5, 3, 11, 12, 16}. In worst case scenario, every single prohibited pattern is found in five independent cycle as illustrated in Fig. 8b. Comparison result between MaxCA and ELCA on this given set of PPS have been enlisted in Table 2.

Advantages of our proposed methodology over MaxCA for fault coverage in random pattern generation, is reported in Table 2. In proposed ELCA, the cycles containing any prohibited pattern is excluded from generating random patterns.

Data sets generated by these different RNGs have been collected to visualize the randomness quality of the corresponding RNGs. The randomness quality graph is shown in Fig. 9. Figure 9 is based on MaxCA for <90, 90, 90, 90, 90, 150> and ELCA for <153, 153, 153, 153, 153, 153>.

Fig. 9
figure 9

Randomness quality graph for different CA-PRNGs

Full size image

Different degrees of randomness of the corresponding RNGs are represented in Fig. 3. The graph shows that the Recursive PRNG is having the least degree of randomness where as Max-Length CA PRNG and ELCA PRNG shares almost equal degree of randomness among themselves and both of them are having the maximum degree of randomness compared to all other RNGs.

‘P value’ is generated in Diehard test and it is uniform [0, 1) for a condition where the input file is contained with truly independent random bits [5]. Degree of randomness achieved by MaxCA random number generators in Diehard tests are reported in Table 3.

Table 3 Performance result through Diehard for different n-values in MaxCA based RNG
Full size table

Table 3 and Fig. 10 have emphasized that the degree of randomness achieved in MaxCA for different cell sizes in terms of the totalnumber of Diehard tests passes. Degree of randomness is graphically represented in Fig. 10.

Fig. 10
figure 10

Randomness quality for MaxCA

Full size image

Increased degree of randomness for MaxCA PRNG with the increase of values of ‘n’ has been reported in Table 3 and Fig. 10.

The results obtained from Table 4 and Fig. 11 ensures that the proposed random number generator is enriched with maximum degree of randomization with a reference to the number of Diehard test passes. This result is similar to the result achieved for MaxCA based RNG. The various complexities of these two CA based methodologies are presented in Table 5. Table 5 has been reported based on the information as reported in Table 2.

Table 4 Performance result through Diehard for different CA-PRNGs
Full size table
Fig. 11
figure 11

Diehard performance graph

Full size image
Table 5 Complexity comparison between MaxCA and proposed methodology
Full size table

Space complexity has been reported in Table 5 and it is same for both procedures as total length of an n-cell CA is same for both the cases, but there are some changes in other complexities. Other complexities have been improved in case of our proposed methodology. The proposed methodology is allowed only to generate random patterns from smaller cycles that exclude PPS. PPS exclusion feature from the main cycle, improves the design and searching complexities.

6 Conclusion

Quality of randomness achieved from the various samples of random data sets has been verified by Diehard tests. The number of passes shows the quality of randomness achieved by particular method. Experimental result shows that the randomness achieved from the random data sets produced through ELCA is having the maximum randomness and this degree of randomness is same as compared to MaxCA. Hence this methodology is suitable for generating random sequences as the cost associated is much cheaper in terms of time complexity and hardware implementation. The ELCA uses only the sub cycle which consists of lesser number of states than of MaxCA. Thus time complexity has been reduced. The time complexity of this proposed methodology maintains a linear time complexity with increased number of cells in the CA. It is also convenient that ELCA based PRNG is more flexible as PPS is completely excluded from random pattern generating cycle.