Unsteady MHD Flow of a Visco-Elastic Fluid Along Vertical Porous Surface with Chemical Reaction

Abstract

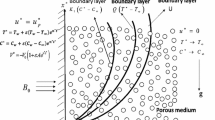
An unsteady magneto hydrodynamic natural convection flow of a visco-elastic (Walters’ fluid (Model B′)) incompressible electrically conducting fluid along an infinite hot vertical porous surface with fluctuating free stream as well as suction velocity in the presence of chemical reaction has been studied. The solutions of momentum, energy, and species concentration equations under Boussinesq approximation are obtained analytically by employing successive perturbation technique. The expressions for the skin friction, Nusselt number and Sherwood number are also derived. The variations in the fluid velocity, temperature and concentration are shown graphically whereas numerical values of skin-friction, Nusselt number and Sherwood number are presented in a tabular form for various values of pertinent flow parameters.

Appendix

$$ m_{1} = \frac{{ - P_{r} + \sqrt {P_{r}^{2} + i\omega P_{r} } }}{2}, \quad m_{2} = - \left( {\frac{{P_{r} + \sqrt {P_{r}^{2} + i\omega P_{r} } }}{2}} \right),\quad m_{3} = \frac{{( - S_{c} + \sqrt {S_{c}^{2} + 4K_{c} S_{c} } )}}{2}, \quad m_{4} = - \left( {\frac{{S_{c} + \sqrt {S_{c}^{2} + 4K_{c} S_{c} } }}{2}} \right),\quad m_{5} = \frac{{\left( { - Sc + \sqrt {S_{c}^{2} + 4\left( {K_{c} + i\omega /4} \right)S_{c} } } \right)}}{2},_{{}} \quad m_{6} = - \left( {\frac{{S_{c} + \sqrt {S_{c}^{2} + 4\left( {K_{c} + i\omega /4} \right)S_{c} } }}{2}} \right) ,\quad m_{7} = \frac{{ - 1 + \sqrt {1 + 4\left( {M^{2} + \frac{1}{{k_{p} }}} \right)} }}{2},_{{}} \quad m_{8} = \frac{{ - \left( {1 + \sqrt {1 + 4\left( {M^{2} + \frac{1}{{k_{p} }}} \right)} } \right)}}{2}, \quad A_{1} = \frac{{ - 1 + \sqrt {1 + 4\left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)} }}{2},_{{}} A_{2} = \frac{{ - \left( {1 + \sqrt {1 + 4(M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4})} } \right)}}{2},\quad I_{ 1} = P_{r}^{2} - P_{r} - \left( {M^{2} + \frac{1}{{k_{p} }}} \right),\;I_{2} = m_{4}^{2} + m_{4} - \left( {M^{2} + \frac{1}{{k_{p} }}} \right),\;I_{3} = \frac{{G_{r} }}{{I_{1} }},\,I_{4} = \frac{{G_{m} }}{{I_{2} }},\quad I_{5} = 2m_{8} + 1,\;I_{6} = \frac{{ ( 1- I_{ 3} - I_{ 4} ) { }m_{ 8}^{ 3} }}{{I_{5} }},\;I_{7} = \frac{{P_{r}^{ 3} I_{3} }}{{I_{1} }},\;I_{8} = \frac{{m_{ 4}^{ 3} I_{4} }}{{I_{2} }},\;I_{9} = I_{7} - I_{8} ,\,I_{10} = \frac{{G_{r} 4iP_{r} }}{\omega },\quad I_{11} = \frac{{m_{4} 4i}}{\omega },I_{12} = \frac{{I_{10} }}{{I_{1} - \frac{i\omega }{4}}},I_{13} = \frac{{I_{10} }}{{m_{2}^{2} + m_{2} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},\quad I_{14} = \frac{{ (I_{ 3} + I_{ 4} { - 1)}m_{ 8} }}{{m_{8}^{2} + m_{8} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},I_{15} = \frac{{{\text{I}}_{ 3} P_{r} }}{{I_{1} - \frac{i\omega }{4}}},I_{16} = \frac{{I_{ 4} m_{4} }}{{I_{2} - \frac{i\omega }{4}}},\quad I_{17} = \frac{{G_{m} I_{11} }}{{m_{6}^{2} + m_{6} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},I_{18} = \frac{{G_{m} I_{11} }}{{I_{2} - \frac{i\omega }{4}}} ,\quad I_{19} = I_{12} + I_{15} , \quad I_{20} = I_{16} + I_{18} ,\quad I_{21} = I_{19} - I_{13} + I_{14} - I_{20} + I_{17} - 1,\quad I_{22} = - I_{3} P_{r}^{3} - I_{7} P_{r} - I_{19} P_{r}^{3} - I_{19} P_{r}^{2} \frac{i\omega }{4},I_{23} { = (1} - I_{ 3} - I_{ 4} )m_{ 8}^{ 3} - I_{9} m_{8} + I_{14} m_{8}^{3} - I_{14} m_{8}^{2} \frac{i\omega }{4},\quad I_{23} { = (1} - I_{ 3} - I_{ 4} )m_{ 8}^{ 3} - I_{9} m_{8} + I_{14} m_{8}^{3} - I_{14} m_{8}^{2} \frac{i\omega }{4},\quad I_{24} = I_{4} m_{4}^{3} - I_{8} m_{4} - I_{20} m_{4}^{3} + I_{20} m_{4}^{2} \frac{i\omega }{4},I_{25} = \frac{{I_{21} A_{2}^{2} \frac{i\omega }{4}\, - \,I_{21} A_{2}^{3} }}{{2A_{2} + 1}},\quad I_{26} = \frac{{I_{13} m_{2}^{2} \frac{i\omega }{4}\, - \, I_{13} m_{2}^{3} }}{{m_{2}^{2} + m_{2} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},\;I_{27} = \frac{{I_{17} m_{6}^{3} - I_{17} m_{6}^{2} \frac{i\omega }{4}}}{{m_{6}^{2} + m_{6} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},\;I_{28} = \frac{{I_{22} }}{{I_{1} - \frac{i\omega }{4}}},\quad I_{29} = \frac{{I_{ 2 3} }}{{m_{8}^{2} + m_{8} - \left( {M^{2} + \frac{1}{{k_{p} }} + \frac{i\omega }{4}} \right)}},\;I_{30} = \frac{{I_{ 2 4} }}{{I_{2} - \frac{i\omega }{4}}},\;I_{31} = - \left( {I_{28} + I_{30} + I_{26} + I_{27} + I_{29} } \right).$$