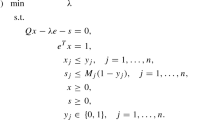Abstract
We present an integer linear formulation that uses the so-called “distance variables” to solve the quadratic assignment problem (QAP). The formulation performs particularly well for problems with Manhattan distance matrices. It involves \(O(n^2)\) variables. Valid equalities and inequalities are proposed divided into two families. First, a family of inequalities valid for any quadratic assignment problems, and second, a family valid only for problems with Manhattan distance matrices, for which we exploit metric properties, as well as an algebraic characterization that Mittelman and Peng (SIAM J Opt 2010:20(6), 3408–3426, 2010) recently proved. We numerically tested the lower bound provided by the linear relaxation using instances of the quadratic assignment problem library (QAPLIB) with randomly generated distance matrices, as well as Manhattan distance matrices. Our results are compared with the best known lower bounds. For Manhattan distance matrices, the formulation gives a very competitive lower bound in a short computational time, improving seven best lower bounds of QAPLIB instances for which no optimality proofs exist.
Similar content being viewed by others
References
Adams WP, Guignard M, Hahn PM, Hightower WL (2007) A level-2 reformulation-linearization-technique bound for the quadratic assignment problem. Disc Opt 180:983–996
Adams WP, Johnson TA (1994) Improved linear programming-based lower bounds for the quadratic assignment problem. DIMACS Ser Disc Math Theor Comput Sci 16:43–75
Adams WP, Sherali HD (1990) Linearization strategies for a class of zero-one mixed integer programming problems. Oper Res 38(2):217–226
Amaral ARS, Caprara A, Letchford AN, Salazar-Gonzáles JJ (2008) A new lower bound for the minimum arrangement of a graph. Electron Notes Disc Math 30:87–92
Balinski ML, Russakoff A (1974) On the assignment polytope. SIAM Rev 16:516–525
Birkhoff G (1946) Tres observaciones sobre el algebra lineal. Rev Univ Nac Tucum (A) 5:147–151
Burer S, Vandenbussche D (2006) Solving lift-and-project relaxations of binary integer programs. SIAM J Opt 16(3):726–750
Burkard RE, Karisch SE, Rendl F (1997) Qaplib— a quadratic assignment problem library. J Global Opt 10:391–403
Caprara A, Letchford AN, Salazar-González JJ (2011) Decorous lower bounds for minimum linear arrangement. INFORMS J Comput 23(1):26–40
Caprara A, Salazar-González JJ (2005) Laying out sparse graphs with provably minimum bandwidth. INFORMS J Comput 17:356–373
Eschermann B, Wunderlich HJ (1990) Optimized synthesis of self-testable finite state machines. In: 20th International symposium on fault-tolerant computing (FFTCS 20), Newcastle upon Tyne (26–28th June, 1990)
Fischetti M, Monaci M, Salvagnin D (2012) Three ideas for the quadratic assignment problem. Oper Res 60:954–964
Floyd RW (1962) Algorithm 97. Commun ACM 5:345
Fortet R (1959) L’algèbre de boole et ses applications en recherche opérationnelle. Cahier du Centre d’Etudes de Recherche Opérationnelle 1:5–36
Fortet R (1960) Application de l’algèbre de boole en recherche opérationnelle. Revue Française de Recherche Opérationnelle 4:17–26
Frieze AM, Yadegar J (1983) On the quadratic assignment problem. Disc Appl Math 5:89–98
Garey M, Johnson D (1979) Computers and intractibility: a guide to the theory of NP-completeness. W.H. Freeman & Company, London
Gilmore PC (1962) Optimal and suboptimal algorithms for the quadratic assignment problem. J Soc Indu Appl Math 10(2):305–313
Glover F (1975) Improved linear integer programming formulations of nonlinear integer problems. Manag Sci 22(4):455–460
Gonçalves AD, Drummond LMA, Pessoa AA, Hahn PM (2013) Improving lower bounds for the quadratic assignment problem by applying a distributed dual ascent algorithm. Corr abs/1304.0267
Hadley SW, Rendl E, Wolkowicz H (1992) A new lower bound via projection for the quadratic assignment problem. Math Oper Res 17:727–739
Hahn PM, Zhu YR, Guignard M, Hightower WL, Saltzman MJ (2012) A level-3 reformulation-linearization technique-based bound for the quadratic assignment problem. INFORMS J Comput 24(2):202–209
Karisch SE, Rendl F (1995) Lower bounds for the quadratic assignment problem via triangle decompositions. Math Program 71:137–151
Karish SE (1995) Nonlinear approaches for quadratic assignment and graph partition problems. Ph.d. thesis, Technical University Graz, Austria
Kaufman L, Broeckx F (1978) An algorithm for the quadratic assignment problem using benders decomposition. Eur J Oper Res 2:204–211
Koopmans TC, Beckmann MJ (1957) Assignment problems and the location of economic activities. Econometrica 25:53–76
Lawler EL (1963) The quadratic assignment problem. Manag Sci 9(4):586–599
Liu W, Vanelli A (1995) Generating lower bounds for the linear arrangement problem. Disc Appl Math 59:137–151
Mittelman H, Peng J (2010) Estimating bounds for quadratic assignment problems associated with hamming and manhattan distance matrices based on semidefinite programming. SIAM J Opt 20(6):3408–3426
Nemhauser GL, Wolsey LA (1979) Integer and combinatorial optimization. Wiley, New Jersey
Nugent CE, Vollman TE, Ruml J (1968) An experimental comparison of techniques for the assignment of facilities to locations. Oper Res 16(1):150–173
Nyberg A, Westerlund T (2012) A new exact discrete linear reformulation of the quadratic assignment problem. Eur J Oper Res 220(2):314–319
Rendl F, Sotirov R (2007) Bounds for the quadratic assignment problem using the bundle method. Math Program 109:505–524
Resende MGC, Ramakrishnan KG, Drezner Z (1995) Computing lower bounds for the quadratic assignment problem with an interior point algorithm for linear programming. Oper Res 43(5):781–791
Scriabin M, Vergin RC (1975) Comparison of computer algorithms and visual based methods for plant layout. Manag Sci 22:172–187
Skorin-Kapov J (1990) Tabu search applied to the quadratic assingnment problem. ORSA J Comput 2(1):33–45
Taillard ED (1991) Robust tabu search for the quadratic assingnment problem. Parallel Comput 17:443–455
Taillard ED (1995) Comparison of iterative searches for the quadratic assingnment problem. Location Sci 3:87–105
Thonemann UW, Bölte A (1994) An improved simulated annealing algorithm for the quadratic assignment problem. Working paper, School of Business, Department of Production and Operations Research, University of Paderborn, Germany
Warshall S (1962) A theorem on boolean matrix. J ACM 9:11
Wilhem MR, Ward TL (1987) Solving quadratic assignment problems by simulated annealing. IIE Trans 19(1):107–119
Zhao Q (1996) Semidefinite programming for assignment and partitioning problems. Ph.d. thesis, University of Waterloo, Ontario, Canada
Zhao Q, Karisch SE, Rendl F, Wolkowicz H (1998) Semidefinite relaxations for the quadratic assignment problem. J Combin Opt 2:71–109
Acknowledgments
We thank Judith Bordt, as well as the three referees, for their careful readings and useful comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Proof of Theorem 6
Proof
Let us prove that the points defined in Theorem 6,
with \(1 \le r < s \le n, and ~(r,s) \notin \{(i_0,j_0);(i_0,h_0);(j_0,h_0)\)}, are \(n(n-1)/2\) affinely independent points.
Let \(\alpha ^0\), \(\alpha ^{rs}\), \(\alpha ^{m+1}\), and \(\alpha ^{m+2}\) be some associated scalars satisfying
For any fixed values \(r_0\) and \(s_0\) such that \(1 \le r_0 < s_0 \le n, (r_0,s_0) \notin \{(i_0,j_0);(i_0,h_0);(j_0,h_0)\}\), the equation (23) gives
Equation (24) implies
It follows that
Thus
These equations together with equation (26) imply that \(\alpha ^0 = \alpha ^{m+2} = \alpha ^{m+2} = 0\). Thus the points are, by definition, affinely independent. \(\square \)
Proof of Theorem 7
Proof
Let us prove that the points defined in Theorem 7,
with \(1 \le r < s \le n, (r,s) \notin \{(i_0,j_0);(i_0,h_0);(j_0,h_0)\}\), are \(n(n-1)/2\) affinely independent points.
Let \(\alpha ^0\), \(\alpha ^{rs}\), \(\alpha ^{i_0 j_0}\), and \(\alpha ^{i_0 h_0}\) with \(1 \le r < s \le n \) and \((r,s) \notin \{(i_0,j_0);(i_0,h_0);(j_0,h_0)\}\), be some scalars satisfying
For \(i_0\) and \(j_0\), the Eq. (27) gives
And (28) \(\Rightarrow \) \(\alpha ^{i_0 j_0} = 0\).
Similarly,
Because \(\alpha ^{i_0 h_0} = \alpha ^{i_0 j_0} = 0\), and because the vectors \(D^0\) and \(D^{rs}\) are affinely independent for a sufficient value of \(M\), the scalars \(\alpha ^0\) and \(\alpha ^{rs}\) are also null, which concludes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Gueye, S., Michelon, P. A linear formulation with \(O(n^2)\) variables for quadratic assignment problems with Manhattan distance matrices. EURO J Comput Optim 3, 79–110 (2015). https://doi.org/10.1007/s13675-014-0033-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13675-014-0033-4