1 Introduction

During the past decades, the interest in utilizing multiple sources of remotely sensed (RS) data in addition to field data has increased considerably in order to make forest inventories cost efficient (e.g., Wulder et al. 2012). When conducting a forest inventory, RS data can be incorporated at two different stages: the design stage and the estimation stage. In the design stage, RS data are used for stratification (e.g., McRoberts et al. 2002) and unequal probability sampling (e.g., Saarela et al. 2015a), they may be used for balanced sampling (Grafström et al. 2014) aiming at improving estimates of population parameters. To utilize RS data at the estimation stage, either model-assisted estimation (Särndal et al. 1992) or model-based inference (Matérn 1960) can be applied. While model-assisted estimators describe a set of estimation techniques within the design-based framework of statistical inference, model-based inference constitutes is a different inferential framework (Gregoire 1998). When applying model-assisted estimation, probability samples are required and relationships between auxiliary and target variables are used to improve the precision of population parameter estimates. In contrast, the accuracy of estimation when assessed in a model-based framework relies largely on the correctness of the model(s) applied in the estimators (Chambers and Clark 2012). While this dependence on the aptness of the model may be regarded as a drawback, this mode of inference also has advantages over the design-based approach. For example, in some cases, smaller sample sizes might be needed for attaining a certain level of accuracy, and in addition, probability samples are not necessary, which is advantageous for remote areas with limited access to the field.

While several sources of auxiliary information can be applied straightforwardly in the case of model-assisted estimation following established sampling theory (e.g., Gregoire et al. 2011; Massey et al. 2014; Saarela et al. 2015a), this issue has been less well explored for model-based inference for the case when the different auxiliary variables are not available for the entire population. However, recent studies by Ståhl et al. (2011) and Ståhl et al. (2014) and Corona et al. (2014) demonstrated how probability samples of auxiliary data can be combined with model-based inference. This approach was termed “hybrid inference” by Corona et al. (2014) to clarify that auxiliary data were collected within a probability framework.

A large number of studies have shown how several sources of RS data can be combined through hierarchical modeling for mapping and estimation of forest attributes such as growing stock volume (GSV) or biomass over large areas. For example, Boudreau et al. (2008) and Nelson et al. (2009) used a combination of the Portable Airborne Laser System (PALS) and the Ice, Cloud, and land Elevation/Geoscience Laser Altimeter System (ICESat/GLAS) data for estimating aboveground biomass for a 1.3 Mkm 2 forested area in the Canadian province of Québec. A Landsat 7 Enhanced Thematic Mapper Plus (ETM+) land cover map was used to delineate forest areas from non-forest and as a stratification tool. These authors used the PALS data acquired on 207 ground plots to develop stratified regression models linking the biomass response variable to PALS metrics. They then used these ground-PALS models to predict biomass on 1325 ICESat/GLAS pulses that have been overflown with PALS, ultimately developing a regression model linking the biomass response variable to ICESat/GLAS waveform parameters as predictor variables. The latter model was used to predict biomass across the entire Province based on 104044 filtered GLAS shots. A similar approach was applied in a later study by Neigh et al. (2013) for assessment of forest carbon stock in boreal forests across 12.5 ± 1.5 Mkm 2 for five circumpolar regions – Alaska, western Canada, eastern Canada, western Eurasia, and eastern Eurasia. The latest study of this kind is from Margolis et al. (2015), where the authors applied the approach for assessment of aboveground biomass in boreal forests of Canada (3,326,658 km 2) and Alaska (370,074 km 2). The cited studies have in common that they ignore parts of the models’ contribution to the overall uncertainty of the biomass (forest carbon stock) estimators, i.e., they can be expected to underestimate the variance of the estimators.

With non-nested models, the assessment of uncertainty is straightforward. McRoberts (2006) and McRoberts (2010) used model-based inference for estimating forest area using Landsat data as auxiliary information. The studies were performed in northern Minnesota, USA. Ståhl et al. (2011) presented model-based estimation for aboveground biomass in a survey where airborne laser scanning (ALS) and airborne profiler data were available as a probability sample. The study was performed in Hedmark County, Norway. Saarela et al. (2015b) analysed the effects of model form and sample size on the accuracy of model-based estimators through Monte Carlo simulation for a study area in Finland. However, model-based approaches that account correctly for hierarchical model structures in forest surveys still appear to be lacking.

In this study, we present a model-based estimation framework that can be applied in surveys that use three data sources, in our case Landsat, ALS and field measurements, and hierarchically nested models. Estimators of population means, their variances and corresponding variance estimators are developed and evaluated for different cases, e.g., when the model random errors are homoskedastic and heteroskedastic and when the uncertainty due to one of the model stages is ignored. The study was conducted using a simulated population resembling the boreal forest conditions in the Kuortane region, Finland. The population was created using a multivariate probability distribution copula technique (Nelsen 2006). This allowed us to apply Monte Carlo simulations of repeated sample draws from the simulated population (e.g., Gregoire 2008) in order to analyse the performance of different population mean estimators and the corresponding variance estimators.

2 Simulated population

The multivariate probability distribution copula technique is a popular tool for multivariate modelling. Ene et al. (2012) pioneered the use of this technique to generate simulated populations which mimic real-world, large-area forest characteristics and associated ALS metrics. Copulas are mathematical functions used to model dependencies in complex multivariate distributions. They can be interpreted as d-dimensional variables on \(\left [0,1\right ]^{d}\) with uniform margins and are based on Sklar’s theorem (Nelsen 2006), which establishes a link between multivariate distributions and their univariate margins. For arbitrary dimensions, multivariate probability densities are often decomposed into smaller building blocks using the pair-copula technique (Aas et al. 2009). In this study, we applied C-vine copulas modeled with the package “VineCopula” (Schepsmeier et al. 2015) of the statistical software R (Core Team 2015). As reference data for the C-vine copulas modeling, a dataset from the Kuortane region was employed. The reference set consisted of four ALS metrics: maximum height (h\(_{\max }\)), the 80th percentile of the distribution of height values (h 80), the canopy relief ratio (CRR), and the number of returns above 2 m divided by the total number of returns as a measure for canopy cover (p veg), digital numbers of three Landsat spectral bands: green (B20), red (B30) and shortwave infra-red (B50), and GSV values per hectare from field measurements using the technique of Finnish national forest inventory (NFI) (Tomppo 2006). For details about the reference data, see Appendix A.

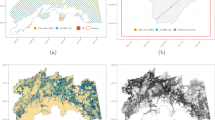
A copula population of 3×106 observations was created, based on which GSV was distributed over the study area using nearest neighbour imputation with the Landsat and ALS variables as a link, and a sample of 818,016 observations corresponding to the 818,016 grid cells of 16m×16m size, belonging to the land-use category forest. The selected sample of 818,016 elements is our simulated population with simulated Landsat spectral values, ALS metrics and GSV values (Saarela et al. 2015b). An overview of the study population is presented in Fig. 1:

Fig. 1
figure 1

The Kuortane study area. The image was shown at the SilviLaser 2015 - ISPRS Geospatial Week where the study’s preliminary results were presented (Saarela et al. 2015c)

Full size image

3 Methods

3.1 Statistical approach

The model-based approach is based on the concept of a superpopulation model. Any finite population of interest is seen as a sample drawn from a larger universe defined by the superpopulation model (Cassel et al. 1977). For large populations, the model has fixed parameters, whose values are unknown, and random elements with assigned attributes. The model-based survey for a finite population mean approximately corresponds to estimating the expected value of the superpopulation mean (e.g., Ståhl et al. 2016). Thus, in this study, our goal was to estimate the expected value of the superpopulation mean, E(μ), for a large finite population U with N grid cells as the population elements. Our first source of information is Landsat auxiliary data, which are available for each population element (grid cell). The second information source is a sample of M grid cells, denoted S a . Each grid cell in S a has two sets of RS auxiliary data available: Landsat and ALS. The third source of information is a subsample S of m grid cells, selected from S a . For each element in S, Landsat, ALS, and GSV values are available. For simplicity, simple random sampling without replacement was assumed to be performed in both phases of sampling. The size of S was 10 % of S a , and S a ranged from M=500 to M=10,000 grid cells, i.e., S ranged from m=50 to m=1000. We applied ordinary least square (OLS) estimators for estimating the regression model parameters and their covariance matrices for models that relate a response variable in one phase of sampling to the auxiliary data. One such example is ALS metrics regressed against GSV in the sample S. The OLS estimator was applied under the usual assumptions, i.e., (i) independence, assuming that the observations are identically and independently distributed (i.i.d.); this assumption is guaranteed by simple random sampling; (ii) exogeneity, assuming that the (normally distributed) errors are uncorrelated with the predictor variables, and (iii) identifiability, assuming that there is one unique solution for the estimated model parameters, i.e., (X T X) has full column rank.

Our study focused on the following cases:

Case A: :

Model-based estimation, where Landsat data are available wall-to-wall and GSV values are available for the population elements in the sample S. In the following sections, the case is also referred to as standard model-based inference.

Case B: :

Two-phase model-based estimation, where ALS data are available for S a and GSV values for the subsample S. This case is also referred to as hybrid inference (Ståhl et al. 2016), since it utilizes both model-based inference and design-based inference.

Case C: :

Model-based estimation based on hierarchical modeling, with wall-to-wall Landsat data as the first source of information, ALS data from the sample S a as the second information source, and GSV data from the subsample S as the third source of information. The case is referred to as model-based inference with hierarchical modeling.

Case C was separated into three sub-cases. The difference between the first two concerns the manner in which the three sources of data were utilized in the estimators and the corresponding variance and variance estimators. The third sub-case was introduced since it reflects how this type of nested regression models have been used in previous studies by simply ignoring the model step from GSV to GSV predictions based on ALS data, i.e., by treating the GSV predictions as if they were true values (e.g., Nelson et al. 2009; Neigh et al. 2011, 2013).

C.1: :

Predicting ALS predictor variables from Landsat data – two-stage least squares regression. − In this case information from the subsample S was used to estimate regression model parameters linking GSV values as responses with ALS variables as predictors. Information from S a was then used to estimate a system of regression models linking ALS predictor metrics as response variables to Landsat variables as predictors. Based on Landsat data ALS predictor variables were then predicted for each population element and utilized for predicting GSV values with the first model. The reason for this rather complicated approach was that variances and variance estimators could be straightforwardly derived based on two-stage least squares regression theory (e.g., Davidson and MacKinnon 1993).

C.2: :

Predicting GSV values from ALS data – hierarchical model-based estimation. − In this case a model based on ALS data was used to predict GSV values for all elements in S a . The predicted GSV values were then used for estimating a regression model linking the predicted GSV as a response variable with Landsat variables as predictors. This model was then applied to all population elements in order to estimate the GSV population mean.

C.3: :

Ignoring the uncertainty due to predicting GSV based on ALS data—simplified hierarchical model-based estimation. In this case, the estimation procedure was the same as in C.2, but in the variance estimation we ignored the uncertainty due to predicting GSV values from ALS data. As mentioned previously, the reason for including this case is that this procedure has been applied in several studies.

3.1.1 Case A: Standard model-based inference

This case follows well-established theory for model-based inference (e.g., Matérn et al. 1960; McRoberts 2006; Chambers & Clark 2012). For estimating the expected value of the superpopulation mean E(μ) (Ståhl et al. 2016), we utilise a regression model linking GSV values as responses with Landsat variables as predictors using information from the subsample S. We assume a linear model to be appropriate, i.e.,

$$ \boldsymbol{y}_{S} = \boldsymbol{Z}_{S}\boldsymbol{\alpha} + \boldsymbol{w}_{S} $$
(1)

where y S is a column vector of length m of GSV values, Z S is a m×(q+1) matrix of Landsat predictors (with a first column of unit values and q is the number of Landsat predictors), α is a column vector of model parameters with length (q+1), and w S is a column vector of random errors with zero expectation, of length m. Under assumptions of independence, exogeneity, and identifiability (e.g., Davidson and MacKinnon 1993), the OLS estimator of the model parameters is

$$ \widehat{\boldsymbol{\alpha}}_{S} = (\boldsymbol{Z}_{S}^{T}\boldsymbol{Z}_{S})^{-1}\boldsymbol{Z}_{S}^{T}\boldsymbol{y}_{S} $$
(2)

where \(\widehat {\boldsymbol {\alpha }}_{S}\) is a (q+1)-length column vector of estimated model parameters.

The estimated model parameters \(\widehat {\boldsymbol {\alpha }}_{S}\) are then used for estimating the expected value of the population mean, \(\widehat {E(\mu )}\), Ståhl et al. (2016):

$$ \widehat{E(\mu)}_{A} = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\alpha}}_{S} $$
(3)

where ι U is a N-length column vector, where each element equals 1/N, Z U is a N×(q+1) matrix of Landsat auxiliary variables, i.e., for the entire population.

The variance of the estimator \(\widehat {E(\mu )}_{A}\) is (Ståhl et al. 2016):

$$ V\Big[\widehat{E(\mu)}_{A}\Big] = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\boldsymbol{Cov}(\widehat{\boldsymbol{\alpha}}_{S} )\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U} $$
(4)

where \(\boldsymbol {Cov}(\widehat {\boldsymbol {\alpha }}_{S})\) is the covariance matrix of the model parameters \(\widehat {\boldsymbol {\alpha }}_{S}\). To obtain a variance estimator, the covariance matrix in Eq. 4 is replaced by an estimated covariance matrix.

When the errors, w S , in Eq. 1, are homoskedastic, the OLS estimator for the covariance matrix is (e.g., Davidson and MacKinnon 1993):

$$ \widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\alpha}}_{S}) = \frac{\widehat{\boldsymbol{w}}_{S}^{T}\widehat{\boldsymbol{w}}_{S}}{m-q-1}(\boldsymbol{Z}_{S}^{T}\boldsymbol{Z}_{S})^{-1} $$
(5)

where \(\widehat {\boldsymbol {w}}_{S}=\boldsymbol {y}_{S} - \boldsymbol {Z}_{S}\widehat {\boldsymbol {\alpha }}_{S}\) is a m-length column vector of residuals over the sample S, using Landsat auxiliary information.

When the errors, w S , in Eq. 1 are heteroskedastic, the covariance matrix can be estimated consistently (HC) with the estimator proposed by White (1980), namely

$$ \widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\alpha}}_{S})=(\boldsymbol{Z}_{S}^{T}\boldsymbol{Z}_{S})^{-1}\Big[ \sum\limits_{i=1}^{m} \hat{w}_{i}^{2}\boldsymbol{z}_{i}^{T}\boldsymbol{z}_{i} \Big](\boldsymbol{Z}_{S}^{T}\boldsymbol{Z}_{S})^{-1} $$
(6)

where \(\hat {w}_{i}\) is a residual and z i is a (q+1)-length row vector of Landsat predictors for the i th observation from the subsample S. To overcome an issue of the squared residuals \(\hat {w}_{i}^{2}\) being biased estimators of the squared errors \({w_{i}^{2}}\), we applied the correction \(\frac {m}{m-q-1}\hat {w}_{i}^{2}\) (Davidson and MacKinnon 1993), i.e., all the \(\hat {w}_{i}^{2}\)-terms in Eq. 6 were multiplied with \(\frac {m}{m-q-1}\).

3.1.2 Case B: Hybrid inference

In the case of hybrid inference, expected values and variances were estimated by considering both the sampling design by which auxiliary data were collected and the model used for predicting values of population elements based on the auxiliary data (e.g., Ståhl et al. 2016). For this case, a linear model linking ALS predictor variables and the GSV response variable were fitted using information from the subsample S

$$ \boldsymbol{y}_{S} = \boldsymbol{X}_{S}\boldsymbol{\beta} + \boldsymbol{e}_{S} $$
(7)

where X S is the m×(p+1) matrix of ALS predictors over sample S, β is a (p+1)-length column vector of model parameters, and e S is an m-length column vector of random errors with zero expectation. Under assumptions of independence, exogeneity and identifiability the OLS estimator of the model parameters is (e.g., Davidson & MacKinnon 1993):

$$ \widehat{\boldsymbol{\beta}}_{S}=(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$
(8)

where \(\widehat {\boldsymbol {\beta }}_{S}\) is a (p+1)-length column vector of estimated model parameters.

Assuming simple random sampling without replacement in the first phase, a general estimator of the expected value of the superpopulation mean \(\widehat {E(\mu )}\) is (e.g., Ståhl et al. 2014):

$$ \widehat{E(\mu)}_{B} = \boldsymbol{\iota}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}}\widehat{\boldsymbol{\beta}}_{S} $$
(9)

where \(\boldsymbol {\iota }_{S_{a}}\) is a M-length column vector of entities 1/M and \(\boldsymbol {X}_{S_{a}}\) is a M×(p+1) matrix of ALS predictor variables.

The variance of the estimator \(\widehat {E(\mu )}_{B}\) is presented by Ståhl et al. (2014, Eq.5, p.5.), ignoring the finite population correction factor:

$$ V\Big[\widehat{E(\mu)}_{B}\Big]=\frac{1}{M}\omega^{2} + \boldsymbol{\iota}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}}\boldsymbol{Cov}(\widehat{\boldsymbol{\beta}}_{S})\boldsymbol{X}_{S_{a}}^{T}\boldsymbol{\iota}_{S_{a}} $$
(10)

where ω 2 is the sample-based population variance from the M-length column vector of \(\widehat {\boldsymbol {y}}_{S_{a}}\)-values and \(\boldsymbol {Cov}(\widehat {\boldsymbol {\beta }}_{S})\) is the covariance matrix of estimated model parameters \(\widehat {\boldsymbol {\beta }}_{S}\). The \(\widehat {\boldsymbol {y}}_{S_{a}}\) values were estimated as

$$ \widehat{\boldsymbol{y}}_{S_{a}}=\boldsymbol{X}_{S_{a}}\widehat{\boldsymbol{\beta}}_{S} $$
(11)

By replacing ω 2 and \(\boldsymbol {Cov}(\widehat {\boldsymbol {\beta }}_{S})\) with the corresponding estimator, we obtain the variance estimator. The sample-based population variance ω 2 is estimated by \(\widehat {\omega ^{2}} = \frac {1}{M-1} {\sum }_{i=1}^{M}(\hat {y}_{i} - \bar {\hat {y}})^{2}\) (cf. Gregoire 2008), and the OLS estimator for \(\boldsymbol {Cov}(\widehat {\boldsymbol {\beta }}_{S})\) is (e.g., Davidson & MacKinnon 1993):

$$ \widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\beta}}_{S}) = \widehat{{\sigma^{2}_{e}}}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1} $$
(12)

where \(\widehat {{\sigma ^{2}_{e}}}=\frac {\widehat {\boldsymbol {e}}_{S}^{T}\widehat {\boldsymbol {e}}_{S}}{m-p-1}\) is the estimated residual variance and \(\widehat {\boldsymbol {e}}_{S}=\boldsymbol {y}_{S}-\boldsymbol {X}_{S}\widehat {\boldsymbol {\beta }}_{S}\) is an m-length column vector of residuals over sample S, using ALS auxiliary information.

In the case of heteroscedasticity, the OLS estimator (Eq. 8) can still be used for estimating the model parameters \(\widehat {\boldsymbol {\beta }}_{S}\) but the covariance matrix is estimated by the HC estimator (White 1980)

$$ \widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\beta}}_{S})=(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\Big[ \sum\limits_{i=1}^{m} \hat{e}_{i}^{2}\boldsymbol{x}_{i}^{T} \boldsymbol{x}_{i} \Big](\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1} $$
(13)

where \(\hat {e}_{i}\) is a residual and x i is the (p+1)-length row vector of ALS predictors for the i th observation from the subsample S. Like for the Case A, we corrected the the squared residuals \(\hat {e}_{i}^{2}\) by a factor \(\frac {m}{m-p-1}\) (Davidson and MacKinnon 1993).

3.1.3 Case C: model-based inference with hierarchical modelling

We begin with introducing the hierarchical model-based estimator for the expected value of the superpopulation mean, E(μ):

$$ \widehat{E(\mu)}_{C} = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U} (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}} (\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$
(14)

where in addition to the already introduced notation, \(\boldsymbol {Z}_{S_{a}}\) is a M×(q+1) matrix of Landsat predictors for the sample S a . In the following, it is shown that the hierarchical model-based estimators for Case C.1 and Case C.2 turn out to be identical under OLS regression assumptions. In the case of weighted least squares (WLS) regression, the estimators differ (see Appendix B).

C.1: :

Predicting ALS predictor variables from Landsat data – two-stage least squares regression.

In this case, we applied a two-stage modeling approach (e.g., Davidson & MacKinnon 1993). Using the sample S a , we developed a multivariate regression model linking ALS variables as responses and Landsat variables as predictors, i.e.

$$\boldsymbol{x}_{{S_{a}}_{j}} = \boldsymbol{Z}_{S_{a}}\boldsymbol{\gamma}_{j} + \boldsymbol{d}_{j}, [j \mathrm{=} 1, 2, ..., (\mathrm{p+1})] $$
(15)

where \(\boldsymbol {x}_{{S_{a}}_{j}}\) is a M-length column vector of ALS variable j, γ j is an (q+1)-length column vector of model parameters for predicted ALS variable j, and d j is an M-length column vector of random errors with zero expectation. We assumed that “all” Landsat predictors Z are used so \(\boldsymbol {Z}_{S_{a}}\) is the same for all variables \(\boldsymbol {x}_{{S_{a}}_{j}}\).

There are (p+1)×(q+1) parameters γ i j in Γ, an (q+1)×(p+1) matrix of model parameters, to be estimated. If we assume simultaneous normality the simultaneous least squares estimator can be used as:

$$ \widehat{\boldsymbol{\gamma}}_{j} = (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{x}_{{S_{a}}_{j}} $$
(16)

We denote \(\widehat {\boldsymbol {\Gamma }}\) as a (q+1)×(p+1) matrix of estimated model parameters, where the first column of \(\widehat {\boldsymbol {\Gamma }}\) is the column vector \((\boldsymbol {Z}_{S_{a}}^{T}\boldsymbol {Z}_{S_{a}})^{-1}\boldsymbol {Z}_{S_{a}}^{T}\boldsymbol {1}_{M}\), which equals \(\begin {pmatrix} 1 & 0 & {\cdots } & 0 \\ \end {pmatrix}_{1\times (q+1)}^{T}\), where 1 M is an M-length column vector of unit values. Thus, we can predict ALS variables for all population elements using Landsat variables, i.e.:

$$ \widehat{\boldsymbol{X}}_{U} = \boldsymbol{Z}_{U}\widehat{\boldsymbol{\Gamma}} $$
(17)

where \(\widehat {\boldsymbol {X}}_{U}\) is a N×(p+1) matrix of predicted ALS variables over the entire population U.

Then, the predicted ALS variables \(\widehat {\boldsymbol {X}}_{U}\) were coupled with the estimated model parameters \(\widehat {\boldsymbol {\beta }}_{S}\) from Eq. 8 to estimate the expected value of the mean GSV:

$$ \widehat{E(\mu)}_{C.1} = \boldsymbol{\iota}_{U}^{T}\widehat{\boldsymbol{X}}_{U}\widehat{\boldsymbol{\beta}}_{S} $$
(18)

To show that this equals Eq. 14, we can rewrite Eq. 18, using Eq. 8, as

$$\widehat{E(\mu)}_{C.1} = \boldsymbol{\iota}_{U}^{T}\widehat{\boldsymbol{X}}_{U}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$

which evidently is equivalent to

$$ \widehat{E(\mu)}_{C.1} = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\Gamma}}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$
(19)

Finally, using the estimator for \(\widehat {\boldsymbol {\Gamma }}\) (Eq. 16), we can rewrite Eq. 19 as

$$\widehat{E(\mu)}_{C.1} = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$

which coincides with Eq. 14 proposed at the start of this section.

Since Eq. 18 can be rewritten as \(\widehat {E(\mu )}_{C.1} = {\sum }_{i=1}^{p+1}\boldsymbol {\iota }_{U}^{T}\hat {\boldsymbol {x}}_{U_{i}}\hat {\beta }_{S_{i}}\), the variance \(V\Big [\widehat {E(\mu )}_{C.1}\Big ]\) of the estimator in Eq. 18 can be expressed as

$$ V\Big[\widehat{E(\mu)}_{C.1}\Big] = \sum\limits_{i=1}^{p+1}\sum\limits_{j=1}^{p+1}Cov(\hat{\beta}_{S_{i}}[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{i}}],\hat{\beta}_{S_{j}}[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{j}}]) $$
(20)

Since \(\widehat {\boldsymbol {\beta }}_{S}\) is based on the subsample S and \(\widehat {\boldsymbol {X}}_{U}\) is based on the sample S a , e S and d j are considered to be independent, and as a consequence we have

$$\begin{array}{@{}rcl@{}} &&Cov(\hat{\beta}_{S_{i}}[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{i}}],\hat{\beta}_{S_{j}}[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{j}}]) = \beta_{i}\beta_{j}Cov([\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{i}}],[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{j}}])\\ &&+ [\boldsymbol{\iota}_{U}^{T}\boldsymbol{x}_{U_{i}}][\boldsymbol{\iota}_{U}^{T}\boldsymbol{x}_{U_{j}}]Cov(\hat{\beta}_{S_{i}},\hat{\beta}_{S_{j}})\\ &&+Cov(\hat{\beta}_{S_{i}},\hat{\beta}_{S_{j}})Cov([\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{i}}],[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{j}}]) \end{array} $$
(21)

The covariances \(Cov(\hat {\beta }_{S_{i}},\hat {\beta }_{S_{j}})\) are given by the elements of the matrix \({\sigma ^{2}_{e}}(\boldsymbol {X}_{S}^{T}\boldsymbol {X}_{S})^{-1}\), where \({\sigma ^{2}_{e}}\) is the variance of the residuals \(\widehat {\boldsymbol {e}}_{S}\), estimated as \(\widehat {{\sigma ^{2}_{e}}} = \frac {\widehat {\boldsymbol {e}}_{S}^{T}\widehat {\boldsymbol {e}}_{S}}{m-p-1}\) (same as in Section 3.1.2). Thus, we estimate \(Cov(\hat {\beta }_{S_{i}},\hat {\beta }_{S_{j}})\) as

$$ \widehat{Cov}(\hat{\beta}_{S_{i}},\hat{\beta}_{S_{j}}) = \widehat{{\sigma^{2}_{e}}}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})_{ij}^{-1} $$
(22)

Further, Eq. 17 gives

$$ Cov([\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{i}}],[\boldsymbol{\iota}_{U}^{T}\hat{\boldsymbol{x}}_{U_{j}}]) = \sum\limits_{k=1}^{q+1}\sum\limits_{l=1}^{q+1}[\boldsymbol{\iota}_{U}^{T}\boldsymbol{z}_{U_{k}}][\boldsymbol{\iota}_{U}^{T}\boldsymbol{z}_{U_{l}}]Cov(\hat{\gamma}_{ki},\hat{\gamma}_{lj}) $$
(23)

The covariance of the estimated model parameters \(\widehat {\boldsymbol {\Gamma }}\), assuming homoskedasticity,

$$ Cov(\hat{\gamma}_{ki},\hat{\gamma}_{lj}) = Cov(\widehat{\boldsymbol{\Gamma}}) = \boldsymbol{\Lambda}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1} $$
(24)

where Λ is a (p+1)×(p+1) matrix of covariances of the M×(p+1) matrix of residuals D, which are estimated as \(\widehat {\boldsymbol {D}}=\boldsymbol {X}_{S_{a}} - \boldsymbol {Z}_{S_{a}}\widehat {\boldsymbol {\Gamma }}\), hence the covariance matrix Λ is estimated as:

$$ \widehat{\boldsymbol{\Lambda}} = \frac{\widehat{\boldsymbol{D}}^{T}\widehat{\boldsymbol{D}}}{M-q-1} $$
(25)

Combining Eqs. 20–24, we can derive the least squares (LS) variance \(V\Big [\widehat {E(\mu )}_{C.1}\Big ]\):

$$\begin{array}{@{}rcl@{}} V_{LS}\Big[\widehat{E(\mu)}_{C.1}\Big] &=& \frac{1}{N^{2}}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\Big(\boldsymbol{z}_{i}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{z}_{j}^{T}\boldsymbol{\beta}^{T}\boldsymbol{\Lambda}\boldsymbol{\beta}\\ &&+{\sigma^{2}_{e}}\boldsymbol{z}_{i}\widehat{\boldsymbol{\Gamma}}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\widehat{\boldsymbol{\Gamma}}^{T}\boldsymbol{z}_{j}^{T}\\ &&+{\sigma^{2}_{e}} \boldsymbol{z}_{i}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{z}_{j}^{T}\sum\limits_{k=1}^{p+1}\sum\limits_{l=1}^{p+1}\lambda_{kl}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})_{kl}^{-1}\Big) \\ &=&\boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\boldsymbol{\beta}^{T}\boldsymbol{\Lambda}\boldsymbol{\beta}\\ &&+ \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\Gamma}}\boldsymbol{Cov}_{OLS}(\widehat{\boldsymbol{\beta}}_{S})\widehat{\boldsymbol{\Gamma}}^{T}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\\ &&+{\sigma^{2}_{e}}\boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\sum\limits_{k=1}^{p+1}\sum\limits_{l=1}^{p+1}\lambda_{kl}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})_{kl}^{-1}\\ \end{array} $$
(26)

Here, λ k l is the [k,l]th element of he matrix Λ.

To derive an estimator \(\widehat {V}_{LS}\Big [\widehat {E(\mu )}_{C.1}\Big ]\) for the variance Eq. 26, we replace β with estimated \(\widehat {\boldsymbol {\beta }}_{S}\), the covariance matrix Λ with \(\widehat {\boldsymbol {\Lambda }}\) from Eq. 25, and \({\sigma ^{2}_{e}}\) with the estimated \(\widehat {{\sigma ^{2}_{e}}}\). Knowing that \(E(\hat {\beta }_{S_{i}}\hat {\beta }_{S_{j}})=\beta _{i}\beta _{j} + Cov(\hat {\beta }_{S_{i}}\hat {\beta }_{S_{j}})\) we have a “minus” sign between the second and third terms of Eq. 26 due to subtracting a product of the estimated covariances. Hence, our estimator for the variance \(V_{LS}\Big [\widehat {E(\mu )}_{C.1}\Big ]\) is

$$\begin{array}{@{}rcl@{}} \widehat{V}_{LS}\Big[\widehat{E(\mu)}_{C.1}\Big] &=& \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\widehat{\boldsymbol{\beta}}_{S}^{T}\widehat{\boldsymbol{\Lambda}}\widehat{\boldsymbol{\beta}}_{S}\\ &&+ \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\Gamma}}\widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\beta}}_{S})\widehat{\boldsymbol{\Gamma}}^{T}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\\ &&- \widehat{{\sigma^{2}_{e}}}\boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\sum\limits_{k=1}^{p+1}\sum\limits_{l=1}^{p+1}\hat{\lambda}_{kl}(\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})_{kl}^{-1}\\ \end{array} $$
(27)

where \(\hat {\lambda }_{kl}\) is a [k,l]th element of the estimated covariance matrix \(\widehat {\boldsymbol {\Lambda }}\) of residuals \(\widehat {\boldsymbol {D}}\).

In the special case when any potential heteroskedasticiy is limited to the GSV function of ALS predictor variables over the sample S, the heteroskedasticity-consistent variance estimator is:

$$\begin{array}{@{}rcl@{}} \widehat{V}_{HC}\Big[\widehat{E(\mu)}_{C.1}\Big] &=& \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\widehat{\boldsymbol{\beta}}_{S}^{T}\widehat{\boldsymbol{\Lambda}}\widehat{\boldsymbol{\beta}}_{S}\\ &&+ \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\Gamma}}\widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\beta}}_{S})\widehat{\boldsymbol{\Gamma}}^{T}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\\ &&-\boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U}\sum\limits_{k=1}^{p+1}\sum\limits_{l=1}^{p+1}\hat{\lambda}_{kl}\widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\beta}}_{S})_{kl}\\ \end{array} $$
(28)
C.2: :

Predicting GSV values from ALS data – hierarchical model-based estimation.

In this case, the predicted GSV variable \(\widehat {\boldsymbol {y}}_{S_{a}}\) is used as a response variable for estimating model parameters linking GSV and Landsat-based predictors over the sample S a , i.e., our assumed model is

$$ \boldsymbol{X}_{S_{a}}\boldsymbol{\beta} = \boldsymbol{Z}_{S_{a}}\boldsymbol{\alpha} + \boldsymbol{w}_{S_{a}} $$
(29)

where \(\boldsymbol {X}_{S_{a}}\boldsymbol {\beta }\) is an M-length column vector of expected values of predicted GSV values \(\widehat {\boldsymbol {y}}_{S_{a}} = \boldsymbol {X}_{S_{a}}\widehat {\boldsymbol {\beta }}_{S}\) using ALS data, α is a (q+1)-length column vector of model parameters linking estimated GSV values and Landsat predictor variables, and \(\boldsymbol {w}_{S_{a}}\) is an M-length column vector of random errors with zero expectation.

In case the \(\boldsymbol {X}_{S_{a}}\boldsymbol {\beta }\) values were observable, the OLS estimator of α would be

$$ \widetilde{\boldsymbol{\alpha}}_{S_{a}} = (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}}\boldsymbol{\beta} $$
(30)

However, we use the \(\boldsymbol {X}_{S_{a}}\widehat {\boldsymbol {\beta }}_{S}\) values and thus our OLS estimator of α is

$$ \widehat{\boldsymbol{\alpha}}_{S_{a}} = (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}}\widehat{\boldsymbol{\beta}}_{S} $$
(31)

Thus, using the estimator \(\widehat {\boldsymbol {\beta }}_{S}\) (Eq. 8), we obtain:

$$ \widehat{\boldsymbol{\alpha}}_{S_{a}} = (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}} (\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} $$
(32)

Then the estimated model parameters \(\widehat {\boldsymbol {\alpha }}_{S_{a}}\) were employed for estimating the expected value of superpopulation mean E(μ):

$$\begin{array}{@{}rcl@{}} \widehat{E(\mu)}_{C.2} &=& \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\widehat{\boldsymbol{\alpha}}_{S_{a}}\\ &=& \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U} (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{X}_{S_{a}} (\boldsymbol{X}_{S}^{T}\boldsymbol{X}_{S})^{-1}\boldsymbol{X}_{S}^{T}\boldsymbol{y}_{S} \end{array} $$

which coincides with Eq. 14. Thus, for models with homogeneous random errors, the estimators of the expected mean are the same for Cases C.1 and C.2.

Based on the estimator \(\widehat {E(\mu )}_{C.2} = \boldsymbol {\iota }_{U}^{T}\boldsymbol {Z}_{U}\widehat {\boldsymbol {\alpha }}_{S_{a}}\), the variance is Ståhl et al. (2016)

$$ V\Big[\widehat{E(\mu)}_{C.2}\Big] = \boldsymbol{\iota}_{U}^{T}\boldsymbol{Z}_{U}\boldsymbol{Cov}(\widehat{\boldsymbol{\alpha}}_{S_{a}})\boldsymbol{Z}_{U}^{T}\boldsymbol{\iota}_{U} $$
(33)

where \(\boldsymbol {Cov}(\widehat {\boldsymbol {\alpha }}_{S_{a}})\) is the covariance matrix of \(\widehat {\boldsymbol {\alpha }}_{S_{a}}\). By replacing the covariance \(\boldsymbol {Cov}(\widehat {\boldsymbol {\alpha }}_{S_{a}})\) with estimated covariance \(\widehat {\boldsymbol {Cov}}(\widehat {\boldsymbol {\alpha }}_{S_{a}})\) in the expression Eq. 33, we obtain a variance estimator.

Under OLS assumptions \(\boldsymbol {Cov}(\widehat {\boldsymbol {\alpha }}_{S_{a}})\) is estimated as

$$\begin{array}{@{}rcl@{}} \widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\alpha}}_{S_{a}}) &=& \frac{\widehat{\boldsymbol{w}}_{S_{a}}^{T}\widehat{\boldsymbol{w}}_{S_{a}}}{M-q-1}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\\ &&+ (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\Big[\boldsymbol{X}_{S_{a}}\widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\beta}}_{S})\boldsymbol{X}_{S_{a}}^{T}\Big]\boldsymbol{Z}_{S_{a}}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\\ \end{array} $$
(34)

where, \(\widehat {\boldsymbol {w}}_{S_{a}}= \boldsymbol {X}_{S_{a}}\widehat {\boldsymbol {\beta }}_{S} - \boldsymbol {Z}_{S_{a}}\widehat {\boldsymbol {\alpha }}_{S_{a}}\) is an M-length vector of residuals.

For the derivation of the estimator in Eq. 34, see Appendix C.

In case of heteroskedasticy of the random errors in the sample S a and the sample S, the HC covariance matrix estimator (White 1980) of the estimated model parameters \(\widehat {\boldsymbol {\alpha }}_{S_{a}}\) was applied (like before, the OLS estimator for \(\widehat {\boldsymbol {\alpha }}_{S_{a}}\) was used):

$$\begin{array}{@{}rcl@{}} \widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\alpha}}_{S_{a}}) &=& (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1} \Big[ \sum\limits_{i=1}^{M} \hat{w}_{i}^{2}\boldsymbol{z}_{i}^{T}\boldsymbol{z}_{i} \Big] (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\\ &&+ (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\boldsymbol{Z}_{S_{a}}^{T}\Big[\boldsymbol{X}_{S_{a}}\widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\beta}}_{S})\boldsymbol{X}_{S_{a}}^{T}\Big]\boldsymbol{Z}_{S_{a}}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1}\\ \end{array} $$
(35)

where \(\hat {w}_{i}^{2}\) is a squared residual for the i th observation in the sample S a . As in Cases A and B, we applied the correction \(\frac {m}{m-q-1}\hat {w}_{i}^{2}\) (Davidson and MacKinnon 1993).

A derivation of the estimator (Eq. 35) is given in see Appendix C.

C.3: :

Ignoring the uncertainty due to predicting GSV values based on ALS data – simplified hierarchical model-based estimation.

This case is included since several studies have used predicted values \(\widehat {\boldsymbol {y}}_{S_{a}}\), using ALS models, as if they were true values, and hence, the uncertainty of their estimation has been ignored. In this case, the same estimator (Eq. 14) for the expected value of mean was used, but for the variance estimator, Eqs. 33 and 34 were applied. Under OLS assumption, the matrix \(\boldsymbol {Cov}(\widehat {\boldsymbol {\alpha }}_{S_{a}})\) was estimated as

$$ \widehat{\boldsymbol{Cov}}_{OLS}(\widehat{\boldsymbol{\alpha}}_{S_{a}})_{C.3} = \frac{\widehat{\boldsymbol{w}}_{S_{a}}^{T}\widehat{\boldsymbol{w}}_{S_{a}}}{M-q-1}(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1} + 0 $$
(36)

In the case of heteroskedasticity, it was estimated as

$$ \widehat{\boldsymbol{Cov}}_{HC}(\widehat{\boldsymbol{\alpha}}_{S_{a}})_{C.3} \,=\,(\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1} \Big[\!\sum\limits_{i=1}^{M} \!\hat{w}_{i}^{2}\boldsymbol{z}_{i}^{T}\boldsymbol{z}_{i} \!\Big] (\boldsymbol{Z}_{S_{a}}^{T}\boldsymbol{Z}_{S_{a}})^{-1} + 0 $$
(37)

Thus, in these estimators, we ignored the uncertainty due to the regression model based on information from the sample S.

3.2 Sampling simulation

Monte Carlo sampling simulation with R=3×104 repetitions was applied. At each repetition, new regression model parameter estimates for the pre-selected variables and their corresponding covariance matrix estimates were computed. Based on the computed model parameters, the expected value of the population mean and its variance were estimated for each case. Averages of estimated values \(\widehat {E(\mu })\) and their estimated variances \(\widehat {V}\Big [\widehat {E(\mu )}\Big ]\) were recorded. Empirical variances \(V\Big [\widehat {E(\mu )}\Big ]_{\text {emp}}\) were computed based on the outcomes from the R repetitions as

$$ V\Big[\widehat{E(\mu)}\Big]_{\text{emp}}=\frac{1}{R-1}\sum\limits_{k=1}^{R}\Bigg[\widehat{E(\mu)}_{k} - \overline{\widehat{E(\mu)}}\Bigg]^{2} $$
(38)

Further, the empirical mean square error (MSE) was estimated based on the R repetitions

$$ MSE\Big[\widehat{E(\mu)}\Big]_{\text{emp}}=\frac{1}{R}\sum\limits_{k=1}^{R}\Big[\widehat{E(\mu)}_{k} - E(\mu)\Big]^{2} $$
(39)

with the known expected value of the superpopulation mean E(μ) = 104.27 m 3 ha −1, as the simulated finite population mean.

For all cases, we calculated the relative bias of the estimated variance

$$ \widehat{RelBIAS} = 100\% \times \frac{\overline{\widehat{V}}\Big[\widehat{E(\mu)}\Big] - V\Big[\widehat{E(\mu)}\Big]_{emp}}{V\Big[\widehat{E(\mu)}\Big]_{emp}} $$
(40)

In order to make sure that the number of repetitions in the Monte Carlo simulations was sufficient, we graphed the average value of the target parameter estimates versus the number of simulation repetitions. For all our cases and estimators, the graphs showed that the estimators stabilized fairly rapidly and that our 3×104 repetitions were sufficient. An example is shown in Fig. 2, for the case of estimating \(\overline {\widehat {V}}_{OLS}\Big [\widehat {E(\mu )}\Big ]\):

Fig. 2
figure 2

The convergence of the estimated model-based variance under OLS assumptions \(\overline {\widehat {V}}_{OLS}\Big [\widehat {E(\mu )}\Big ]\) over the number of repetitions in the Monte Carlo simulations, sample sizes: m = 100 grid cells, M = 1000 grid cells.

Full size image

4 Results

As expected, the accuracy of the model-based estimator with hierarchical modeling (Case C) increased as sample sizes in the two phases increased. The estimator is at least approximately unbiased, because for every group of sample sizes \(MSE_{\text {emp}}\Big [\widehat {E(\mu )}\Big ]\approx V_{\text {emp}}\Big [\widehat {E(\mu )}\Big ]\). The Landsat variables had less predictive power than ALS metrics in prediction GSV; hence, the accuracy of the Case B estimator is higher than the Case A estimator. However, including wall-to-wall Landsat auxiliary information improved the accuracy compared to using ALS sample data alone, i.e., the MSE of Case C is lower than the MSE of Case B (Table 1).

Table 1 Averages of estimated expected values of the superpopulation mean \(\overline {\widehat {E(\mu )}}\) and their estimated analytical variances \(\overline {\widehat {V}}\Big [\widehat {E(\mu )}\Big ]\), corresponding MSE \(MSE\Big [\widehat {E(\mu )}\Big ]\), empirical variances \(V_{emp}\Big [\widehat {E(\mu )}\Big ]\), and estimated relative bias \(\widehat {RelBIAS}\): Case A – standard model-based inference, Case B – hybrid inference, Case C −− model-based inference with hierarchical modelling: C.1 – two-stage lest squares regression, C.2 – hierarchical model-based estimation, C.3 – simplified hierarchical model-based estimation
Full size table

Comparing the performances of the Case C.3 variance estimator and the hierarchical model-based variance estimator of Case C.2, we observed that ignoring the uncertainty due to the GSV-ALS model leads to underestimation of the variance by about 70 % (Table 1).

In Table 2, we present examples of the goodness of fit of the models used in the Case C.2 (and C.3). From Table 2, it can be observed that the goodness of fit was substantially better for the ALS models compared to the Landsat models.

Table 2 Averages of adjusted coefficients of determination \({R^{2}_{a}}\) and estimated residual standard errors \(\widehat {\sigma _{e}}\) and \(\widehat {\sigma _{w}}\) for the ALS- and Landsat-based models developed in Case C.2
Full size table

5 Discussion

In this study, we have presented and evaluated novel estimators and their corresponding variance estimators for model-based inference using three sources of information and hierarchically nested models, for applications in forest inventory combining RS and field data. The estimators were evaluated through Monte Carlo simulation, for the case of estimating the population mean GSV. The estimators and the variance estimators were found to be at least approximately unbiased, unless in the Case C.3 where the uncertainty of one of the models was ignored. The precision of the estimators depended on the number of observations used for developing the models involved; the uncertainties due to both model steps involved were found to substantially contribute to the overall uncertainty of the estimators.

Our first main methodological approach (Case C.1) uses wall-to-wall Landsat data to predict the ALS predictor variables involved when regressing field-measured GSV as a response variable on ALS data. In this way, we emulated wall-to-wall ALS data, which were used for estimating the population mean across the study area. The method is straightforward but rather cumbersome to apply when the ALS models involve several predictor variables. Our second main methodological approach (Case C.2) is more intuitive, since it proceeds by first estimating a model between field GSV and ALS data; subsequently, GSV is predicted for all sample units with ALS data and these predictions are used as responses in modeling GSV based on Landsat data. Finally, wall-to-wall Landsat data are used for making predictions across the entire study area and for estimating the population mean GSV. Compared to the first method, this method is simpler to apply for ALS models with a large number of predictor variables. For models with homogeneous residual variances, fitted using OLS, the estimators obtained from the two different methods are identical, but the variances and variance estimators differ. However, the variance estimates obtained in the simulation study were similar for the two methods.

Several previous studies have combined two sources of RS data and field data in connection with hierarchical model-based estimation of forest resources. Boudreau et al. (2008), Nelson et al. (2009), Neigh et al. (2013), and Margolis et al. (2015) applied estimators of the kind denoted C.3 in this study, i.e., they accounted for only one model step in the assessment of uncertainties. This is pointed out by Margolis et al. (2015), and Neigh et al. (2013) concluded that this would lead to a substantial underestimation of the variance. In our study, with the new set of estimators to specifically address this issue, we found that the underestimation of the variance may be as high as 70 % if the model step linking field and ALS data is ignored in the assessment of uncertainties. However, the magnitude of the underestimation depends on the properties of the models involved and the sample sizes applied for developing the models. Our findings also are important for studies (e.g., Rana et al. 2013; Ota et al. 2014) where ALS data are taken as true values in developing models where other types of RS data are used for stand or plot level predictions of forest attributes such as GSV, biomass, or canopy height.

Compared to hybrid inference using only the ALS sample and field data (Case B), using any of the two main methodological approaches of this study (Cases C.1 and C.2) improved the precision of the estimated mean GSV. Compared to using only wall-to-wall Landsat and field data (Case A), the improvement in precision was very large.

An advantage of model-based inference and thus the estimators we propose is that they do not require probability samples of field or ALS data. Purposive sampling can be applied in all phases. This property makes the proposed inference technique attractive for forest surveys in remote areas, such as Siberia in the Russian Federation and Alaska in the USA, where field plots cannot easily be established in all parts of the target area due to the poor road infra-structure. However, in this study, we applied simple random sampling as a means to provide an objective description of the data collection; further, one of the methods evaluated, i.e., hybrid estimation, requires a probability sample of auxiliary data. Note that simple random sampling was applied in both phases, which to some extent limits the generality of the results since ALS samples are typically acquired as clusters of grid cells (e.g., Gobakken et al. 2012). Ongoing studies are addressing this issue in order to make the proposed type of estimators more general.

The new estimators are derived for both homoskedasticity and heteroscedasticity conditions, regarding the random errors variance. In case of heteroscedasticity, typically the OLS estimator of the covariance matrix of estimated model parameters overestimates the actual variances the model parameters (White 1980; Davidson and MacKinnon 1993). Thus, a heteroskedasticity-consistent estimator should be applied in such cases. In our simulation study, we applied a modified HC estimator; however, our results do not indicate any major difference between using different types of covariance matrix estimators. Another technical detail regards whether or not linear models can always be successfully applied for modelling GSV, as assumed in this study where OLS regression and linear models were applied. With nonlinear models or other parameter estimation techniques the proposed theory would need to be slightly modified.

Although some simplifying assumptions were made, we suggest that the proposed set of estimators (Cases C.1 and C.2) has a potential to substantially contribute to the development of new techniques for large-area forest surveys, utilizing several sources of auxiliary information in connection with model-based inference.