Cauchy-type integrals in several complex variables

Abstract

We present the theory of Cauchy–Fantappié integral operators, with emphasis on the situation when the domain of integration, $D$, has minimal boundary regularity. Among these operators we focus on those that are more closely related to the classical Cauchy integral for a planar domain, whose kernel is a holomorphic function of the parameter $z\in D$. The goal is to prove $L^p$ estimates for these operators and, as a consequence, to obtain $L^p$ estimates for the canonical Cauchy–Szegö and Bergman projection operators (which are not of Cauchy–Fantappié type).

1 Introduction

The purpose of this survey is to study Cauchy-type integrals in several complex variables and to announce new results concerning these operators. While this is a broad field with a very wide literature, our exposition will be focused more narrowly on achieving the following goal: the construction of such operators and the establishment of their $L^p$ mapping properties under “minimal” conditions of smoothness of the boundary of the domain $D$ in question.

The operators we study are of three interrelated kinds: Cauchy–Fantappié integrals with holomorphic kernels, Cauchy–Szegö projections and Bergman projections. In the case of one complex variable, what happens is by now well-understood. Here the minimal smoothness that can be achieved is “near” $C^1$ (e.g., the case of a Lipschitz domain). However when the complex dimension is greater than 1 the nature of the Cauchy–Fantappié kernels brings in considerations of pseudo-convexity (in fact strong pseudo-convexity) and these in turn imply that the limit of smoothness should be “near” $C^2$.

We establish $L^p$-regularity for one or more of these operators in the following contexts:

• When $D$ is strongly pseudo-convex and of class $C^2$;

• When $D$ is strongly $\mathbb{C}$-linearly convex and of class $C^{1,1}$

with $p$ in the range $1<p<\infty$. See Theorems 1–4 for the precise statements.

This survey is organized as follows. In Sect. 2 we briefly review the situation of one complex variable. Section 3 is devoted to a few generalities about Cauchy-type integrals when $n$, the complex dimension of the ambient space, is greater than 1. The Cauchy–Fantappié forms are taken up in Sect. 4 and the corresponding Cauchy–Fantappié integral operators are set out in Sect. 5. Here we adapt the standard treatment in [34, Chapt. IV], but our aim is to show that these methods apply when the so-called generating form is merely of class $C^1$ or even Lipschitz, as is needed in what follows.

The Cauchy–Fantappié integrals constructed up to that point may however lack the basic requirement of producing holomorphic functions, whatever the given data is. In other words, the kernel of the operator may fail to be holomorphic in the free variable $z\in D$. To achieve the desired holomorphicity requires that the domain $D$ be pseudo-convex, and two specific forms of this property, strong pseudo-convexity and strong$\mathbb{C}$-linear convexity are discussed in Sect. 6.

There are several approaches to obtain the required holomorphicity when the domain is sufficiently smooth and strongly pseudo-convex. The initial methods are due to Henkin [17, 18] and Ramirez [33]; a later approach is in Kerzman–Stein [21], which is the one we adopt here. It requires to start with a “locally” holomorphic kernel, and then to add a correction term obtained by solving a $\overline{\mathit{\partial }}$-problem. These matters are discussed in Sects. 7–9. One should note that in the case of strongly $\mathbb{C}$-linearly convex domains, the Cauchy–Leray integral given here requires no correction. So among all the integrals of Cauchy–Fantappié type associated to such domains, the Cauchy–Leray integral is the unique and natural operator that most closely resembles the classical Cauchy integral from one complex variable.

The main $L^p$ estimates for the Cauchy–Leray integral and the Szegö and Bergman projections (for $C^2$ boundaries) are the subject of a series of forthcoming papers; in Sect. 10 we limit ourselves to highlighting the main points of interest in the proofs. For the last two operators, the $L^p$ results are consequences of estimates that hold for the corrected Cauchy–Fantappié kernels, denoted $C_{\mathit{ϵ}}$ and $B_{\mathit{ϵ}}$, that involve also their respective adjoints. Section 11 highlights a further result concerning the Cauchy–Leray integral, also to appear in a separate paper: the corresponding $L^p$ theorem under the weaker assumption that the boundary is merely of class $C^{1,1}$.

A survey of this kind must by the nature of the subject be far from complete. Among matters not covered here are $L^p$ results for the Szegö and Bergman projection and for the Cauchy–Leray integral for other special domains (in particular, with more regularity). For these, see e.g. [2–4, 6–8, 12, 13, 15, 23, 29, 30, 32, 37]. It is to be noted that several among these works depend in the main on good estimates or explicit formulas for the Szegö or Bergman kernels. In our situation these are unavailable, and instead we have to proceed via the Cauchy–Fantappié framework.

A few words about notation: Euclidean volume measure for ${\mathbb{C}}^n\equiv {\mathbb{R}}^{2n}$ ($n\ge 1$) will be denoted $\mathit{dV}$. The notation $\mathrm{b}D$ will indicate the boundary of a domain $D\subset {\mathbb{C}}^n$ ($n\ge 1$) and, for $D$ sufficiently smooth, $d\mathit{\sigma }$ will denote arc-length ($n=1$) or Euclidean surface measure ($n\ge 2$).

2 The Case $n=1$

In the case of one complex dimension the problem of $L^p$ estimates has a long and illustrious history. Let us review it briefly. (Some details can be found in [10, 16, 24], which contain further citations to the literature.)

Suppose $D$ is a bounded domain in $\mathbb{C}$ whose boundary $\mathrm{b}D$ is a rectifiable curve. Then the Cauchy integral is given by

$$\begin{array}{c}\hfill \mathbf{C}(f)(z)=\underset{\mathrm{b}D}{\int }f(w)C(w,z),\text{for}z\in D\end{array}$$

where $C(w,z)$ is the Cauchy kernel

$$\begin{array}{c}\hfill C(w,z)=\frac{1}{2\mathit{\pi }i}\frac{\mathit{dw}}{w-z}\end{array}$$

When $D$ is the unit disc, then a classical theorem of M. Riesz says that the mapping $f\mapsto \mathbf{C}(f){|}_{\mathrm{b}D}$, defined initially for $f$ that are (say) smooth, is extendable to a bounded operator on $L^p(\mathrm{b}D)$, for $1<p<\infty$. Very much the same result holds when the boundary of $D$ is of class $C^{1+\mathit{ϵ}}$, with $\mathit{ϵ}>0$, (proved either by approximating to the result when $D$ is the unit disc, or adapting one of the several methods of proof used in the classical case). However in the limiting case when $\mathit{ϵ}=0$, these ideas break down and new methods are needed. The theorems proved by Calderón, Coifman, McIntosh, Meyers and David (between 1977–1984) showed that the corresponding $L^p$ result held in the following list of increasing generality: the boundary is of class $C^1$; it is Lipschitz (the first derivatives are merely bounded and not necessarily continuous); it is an “Ahlfors-regular” curve.

We pass next to the Cauchy–Szegö projection $\mathbf{S}$, the corresponding orthogonal projection with respect to the Hilbert space structure of $L^2(\mathrm{b}D)$. In fact when $D$ is the unit disc, the two operators $\mathbf{C}$ and $\mathbf{S}$ are identical. Let us now restrict our attention to the case when $D$ is simply connected and when its boundary is Lipschitz. Here a key tool is the conformal map $\mathrm{\Phi }:\mathbb{D}\to D$, where $\mathbb{D}$ is the unit disc. We consider the induced correspondence $\mathit{\tau }$ given by $\mathit{\tau }(f)(e^{i\mathit{\theta }})={({\mathrm{\Phi }}^{\prime }(e^{i\mathit{\theta }}))}^{\frac{1}{2}}f(\mathrm{\Phi }(e^{i\mathit{\theta }}))$, and the fact that $S={\mathit{\tau }}^{-1}{S}_0\mathit{\tau }$, where $S_0$ is the Cauchy–Szegö projection for the disc $\mathbb{D}$. Using ideas of Calderón, Kenig, Pommerenke and others, one can show that $|{\mathrm{\Phi }}^{\prime }{|}^r$ belongs to the Muckenhaupt class $A_p$, with $r=1-p/2$, from which one gets the following. As a consequence, if we suppose that $\mathrm{b}D$ has a Lipschitz bound $M$, then $\mathbf{S}$ is bounded on $L^p$, whenever

• $1<p<\infty$, if $\mathrm{b}D$ is in fact of class $C^1$.

• $p_M^{\prime }<p<p_M$. Here $p_M$ depends on $M$, but $p_M>4$, and $p_M^{\prime }$ is the exponent dual to $p_M$.

There is an alternative approach to the second result that relates the Cauchy–Szegö projection $\mathbf{S}$ to the Cauchy integral $\mathbf{C}$. It is based on the following identity, used in [21]

$$\begin{array}{c}\hfill \mathbf{S}(I-\mathbb{A})=\mathbf{C},\text{where}\mathbb{A}={\mathbf{C}}^{\ast }-\mathbf{C}.\end{array}$$

(2.1)

There are somewhat analogous results for the Bergman projection in the case of one complex dimension. We shall not discuss this further, but refer the reader to the papers cited above.

3 Cauchy integral in ${\mathbb{C}}^n,n>1$; some generalities

We shall see that a very different situation occurs when trying to extend the results of Sect. 2 to higher dimensions. Here are some new issues that arise when $n>1$

• i There is no “universal” holomorphic Cauchy kernel associated to a domain $D$.

• ii Pseudo-convexity of $D$, must, in one form or another, play a role.

• iii Since this condition involves (implicitly) two derivatives, the “best” results are to be expected “near” $C^2$, (as opposed to near $C^1$ when $n=1$).

In view of the non-uniqueness of the Cauchy integral (and its problematic existence), it might be worthwhile to set down the minimum conditions that would be required of candidates for the Cauchy integral. We would want such an operator $\mathbf{C}$ given in the form

$$\begin{array}{c}\hfill \mathbf{C}(f)(z)=\underset{\mathrm{b}D}{\int }f(w)C(w,z),z\in D,\end{array}$$

to satisfy the following conditions:

• (a) The kernel $C(w,z)$ should be given by a “natural” or explicit formula (at least up to first approximation) that involves $D$.

• (b) The mapping $f\mapsto \mathbf{C}(f)$ should reproduce holomorphic functions. In particular if $f$ is continuous in $\overline{D}$ and holomorphic in $D$ then $\mathbf{C}(f)(z)=f(z)$, for $z\in D$.

• (c) $\mathbf{C}(f)(z)$ should be holomorphic in $z\in D$, for any given $f$ that is continuous on $\mathrm{b}D$.

Now there is a formalism (the Cauchy–Fantappié formalism of Fantappié (1943), Leray, and Koppleman (1967)), which provides Cauchy integrals satisfying the requirements (a) and (b) in a general setting. Condition (c) however, is more problematic, even when the domain is smooth. Constructing such Cauchy integrals has been carried out only in particular situations, (see below).

4 Cauchy–Fantappié theory in higher dimension

The Cauchy–Fantappié formalism that realizes the kernel $C(w,z)$ revolves around the notion of generating form: these are a class of differential forms of type $(1,0)$ in the variable of integration whose coefficients may depend on two sets of variables ($w$ and $z$), and we will accordingly write

$$\begin{array}{c}\hfill \mathit{\eta }(w,z)=\sum _{j=1}^n{\mathit{\eta }}_j(w,z){\mathit{dw}}_j\text{with}(w,z)\in U\times V\end{array}$$

to designate such a form. The precise definition is given below, where the notation

$$\begin{array}{c}\hfill 〈\mathit{\eta }(w,z),\mathit{\xi }〉=\sum _{j=1}^n{\mathit{\eta }}_j(w,z){\mathit{\xi }}_j.\end{array}$$

is used to indicate the action of $\mathit{\eta }$ on the vector $\mathit{\xi }\in {\mathbb{C}}^n$.

Definition 1

The form $\mathit{\eta }(w,z)$ is generating at$z$relative to$V$ if there is an open set

$$\begin{array}{c}\hfill U_z\subseteq {\mathbb{C}}^n\setminus \{z\}\end{array}$$

such that

$$\begin{array}{c}\hfill \mathrm{b}V\subset U_z\end{array}$$

(4.1)

and, furthermore

$$\begin{array}{c}\hfill 〈\mathit{\eta }(w,z),w-z〉=\sum _{j=1}^n{\mathit{\eta }}_j(w,z)(w_j-z_j)\equiv 1\text{for}\text{any}w\in U_z.\end{array}$$

(4.2)

We say that $\mathit{\eta }$ is a generating form for$V$ (alternatively, that $V$supports a generating form$\mathit{\eta }$) if for any $z\in V$ we have that $\mathit{\eta }$ is generating at $z$ relative to $V$.

Example 1

Set

$$\begin{array}{c}\hfill \mathit{\beta }(w,z)=|w-z{|}^2\end{array}$$

We define the Bochner–Martinelli generating formto be

$$\begin{array}{c}\hfill \mathit{\eta }(w,z)=\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z)=\sum _{j=1}^n\frac{{\overline{w}}_j-{\overline{z}}_j}{|w-z{|}^2}{\mathit{dw}}_j\end{array}$$

(4.3)

It is clear that $\mathit{\eta }$ satisfies conditions (4.1) and (4.2) for any domain $V$ and for any $z\in V$, with $U_z:={\mathbb{C}}^n\setminus \{z\}$.

The Bochner–Martinelli generating form has several remarkable features. First, it is “universal” in the sense that it is given by a formula (4.3) that does not depend on the choice of domain $V$; secondly, in complex dimension $n=1$ it agrees (up to a scalar multiple) with the classical Cauchy kernel

$$\begin{array}{c}\hfill \frac{1}{2\mathit{\pi }i}\frac{\mathit{dw}}{w-z},w\in U_z:=\mathbb{C}\setminus \{z\}\end{array}$$

and in particular its coefficient ${(w-z)}^{-1}$ is holomorphic as a function of $z\in V$ for any fixed $w\in \mathrm{b}V$. On the other hand, it is clear from (4.3) that for $n\ge 2$ the coefficients of this form are nowhere holomorphic: this failure at holomorphicity is an instance of a crucial, dimension-induced phenomenon which was alluded to in conditions ii. and (c) in Sect. 3 and will be further discussed in Example 2 below and in Sect. 6.

4.1 Cauchy–Fantappié forms

Suppose now that for each fixed $z$$\mathit{\eta }(w,z)$ is a form of type $(1,0)$ in $w$ with coefficients of class $C^1$ in each variable. (We are not assuming that $\mathit{\eta }$ is a generating form). Set

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0(\mathit{\eta })(w,z)=\frac{1}{{(2\mathit{\pi }i)}^n}\mathit{\eta }\wedge {({\overline{\mathit{\partial }}}_w\mathit{\eta })}^{n-1}(w,z)\end{array}$$

(4.4)

where ${({\overline{\mathit{\partial }}}_w\mathit{\eta })}^{n-1}$ stands for the wedge product: ${\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge \cdots \wedge {\overline{\mathit{\partial }}}_w\mathit{\eta }$ performed $(n-1)$-times. We call ${\mathrm{\Omega }}_0(\mathit{\eta })$ the Cauchy-Fantappiè form for$\mathit{\eta }$. Note that ${\mathrm{\Omega }}_0(\mathit{\eta })(w,z)$ is of type $(n,n-1)$ in the variable $w\in U$ while in the variable $z\in V$ it is just a function.

Example 2

The Cauchy–Fantappié form for the Bochner–Martinelli generating form or, for short, Bochner–Martinelli CF form is

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0\left(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}\right)(w,z)=\frac{(n-1)!}{{(2\mathit{\pi }i|w-z{|}^2)}^n}\sum _{j=1}^n({\overline{w}}_j-{\overline{z}}_j){\mathit{dw}}_j\wedge (\underset{\mathit{\nu }\ne j}{\bigwedge }d{\overline{w}}_{\mathit{\nu }}\wedge {\mathit{dw}}_{\mathit{\nu }}).\end{array}$$

Now the Bochner–Martinelli integral is the operator

$$\begin{array}{c}\hfill {\mathbf{C}}_{\mathbf{BM}}f(z)=\underset{w\in \mathrm{b}D}{\int }f(w)C_{\mathit{BM}}(w,z),z\in D,f\in C(\mathrm{b}D)\end{array}$$

where the kernel $C_{\mathit{BM}}(w,z)$ is the Bochner–Martinelli CF form restricted to the boundary; more precisely

$$\begin{array}{c}\hfill C_{\mathit{BM}}(w,z)=j^{\ast }{\mathrm{\Omega }}_0\left(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}\right)(w,z),w\in \mathrm{b}D,z\in D\end{array}$$

where $j^{\ast }$ denotes the pullback of forms under the inclusion

$$\begin{array}{c}\hfill j:\mathrm{b}D\hookrightarrow {\mathbb{C}}^n\end{array}$$

It is clear that such operator is “natural” in the sense discussed in condition (a) in Sect. 3, and we will see in Sect. 5 that this operator also satisfies condition (b), see Proposition 1 in that section. On the other hand, the kernel $C_{\mathit{BM}}(w,z)$ is nowhere holomorphic in $z$: as a result, when $n>1$ the Bochner–Martinelli integral does not satisfy condition (c).

We will now review the properties of Cauchy-Fantappiè forms that are most relevant to us.

Basic Property 1

For any function $g\in C^1(U)$ we have

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0(g(w)\mathit{\eta }(w,z))=g^n(w){\mathrm{\Omega }}_0(\mathit{\eta })(w,z)\text{for}\text{any}w\in U.\end{array}$$

Proof

The proof is a computation: by the definition (4.4), we have

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0\left(g\mathit{\eta }\right)=g\mathit{\eta }\wedge {(\overline{\mathit{\partial }}(g\mathit{\eta }))}^{n-1}\end{array}$$

On the other hand, computing ${(\overline{\mathit{\partial }}(g\mathit{\eta }))}^{n-1}$ produces two kinds of terms:

• (a.) Terms that contain $\overline{\mathit{\partial }}g\wedge \mathit{\eta }$: but these do not contribute to ${\mathrm{\Omega }}_0(g\mathit{\eta })$ because $g\mathit{\eta }\wedge \overline{\mathit{\partial }}g\wedge \mathit{\eta }=0$ (which follows from $\mathit{\eta }\wedge \mathit{\eta }=0$ since $\mathit{\eta }$ has degree $1$);

• (b.) The term $g^{n-1}\overline{\mathit{\partial }}\mathit{\eta }$, which gives the desired conclusion.

$\square$

Suppose, further, that $\mathit{\eta }(w,z)$ is generating at $z$ relative to $V$. Then the following two properties also hold.

Basic Property 2

We have that

$$\begin{array}{c}\hfill {({\overline{\mathit{\partial }}}_w\mathit{\eta })}^n(w,z)=0\text{for}\text{any}w\in U_z.\end{array}$$

(4.5)

Note that if the coefficients of $\mathit{\eta }(·,z)$ are in $C^2(U_z)$, then as a consequence of the fact that $\overline{\mathit{\partial }}\circ \overline{\mathit{\partial }}=0$, we have that ${({\overline{\mathit{\partial }}}_w\mathit{\eta })}^n(w,z)=d_w{\mathrm{\Omega }}_0(\mathit{\eta })(w,z)$ and (4.5) can be formulated equivalently as

$$\begin{array}{c}\hfill d_w{\mathrm{\Omega }}_0(\mathit{\eta })(w,z)=0,w\in U_z.\end{array}$$

Proof

We prove (4.5) in the case: $n=2$ and leave the proof for general $n$ as an exercise for the reader. Thus, writing

$$\begin{array}{c}\hfill \mathit{\eta }={\mathit{\eta }}_1{\mathit{dw}}_1+{\mathit{\eta }}_2{\mathit{dw}}_2\end{array}$$

we obtain

$$\begin{array}{c}\hfill {({\overline{\mathit{\partial }}}_w\mathit{\eta })}^2=-2{\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1\wedge {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\wedge {\mathit{dw}}_1\wedge {\mathit{dw}}_2\end{array}$$

(4.6)

Now

$$\begin{array}{c}\hfill {\mathit{\eta }}_1(w,z)(w_1-z_1)+{\mathit{\eta }}_2(w,z)(w_2-z_2)=1\text{for}\text{any}w\in U_z\end{array}$$

because $\mathit{\eta }$ is generating at $z$, and applying ${\overline{\mathit{\partial }}}_w$ to each side of this identity we obtain

$$\begin{array}{c}\hfill (w_1-z_1){\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1(w,z)+(w_2-z_2){\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2(w,z)=0\text{for}\text{any}w\in U_z\end{array}$$

(4.7)

Recall that $U_z\subset {\mathbb{C}}^2\setminus \{z\}$, see Definition 1, and so

$$\begin{array}{c}\hfill U_z\cap U=U_z^1\cup U_z^2\end{array}$$

where

$$\begin{array}{c}\hfill U_z^1=\{w=(w_1,w_2)\in U_z\cap U,w_1\ne z_1\}\end{array}$$

(4.8)

$$\begin{array}{c}\hfill U_z^2=\{w=(w_1,w_2)\in U_z\cap U,w_2\ne z_2\}\end{array}$$

(4.9)

But for any two sets $A$ and $B$ one has $A\cup B=(A\setminus B)\stackrel{·}{\cup }(B\setminus A)\stackrel{·}{\cup }(A\cap B)$ where $\stackrel{·}{\cup }$ denotes disjoint union. Now, if $w\in U_z^1\setminus U_z^2$ then (4.7) reads

$$\begin{array}{c}\hfill (w_1-z_1){\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1(w,z)=0,w_1\ne z_1\end{array}$$

but this implies

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1(w,z)=0\text{for}\text{any}w\in U_z^1\setminus U_z^2.\end{array}$$

One similarly obtains

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2(w,z)=0\text{for}\text{any}w\in U_z^2\setminus U_z^1).\end{array}$$

We are left to consider the case when $w\in U_z^1\cap U_z^2$; note that since

$$\begin{array}{c}\hfill (w_1-z_1)(w_2-z_2)\ne 0\text{for}\text{any}w\in U_z^1\cap U_z^2\end{array}$$

showing that ${({\overline{\mathit{\partial }}}_w\mathit{\eta })}^2(w,z)=0$ for any $w\in U_z^1\cap U_z^2$ is now equivalent to showing that

$$\begin{array}{c}\hfill (w_1-z_1)(w_2-z_2){({\overline{\mathit{\partial }}}_w\mathit{\eta })}^2(w,z)=0\text{for}\text{any}w\in U_z^1\cap U_z^2\end{array}$$

To this end, combining (4.6) with (4.7) we find

$$\begin{array}{cc}\hfill & (w_1-z_1)(w_2-z_2){({\overline{\mathit{\partial }}}_w\mathit{\eta })}^2(w,z)\hfill \\ \hfill & =2{(w_1-z_1)}^2{\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1(w,z)\wedge {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1(w,z)\wedge {\mathit{dw}}_1\wedge {\mathit{dw}}_2\hfill \end{array}$$

and indeed

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1\wedge {\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1=0\end{array}$$

because ${\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1$ is a form of degree 1. $\square$

Let $\mathit{\eta }(w,z)$ be a form of type $(1,0)$ in the variable $w$ (not necessarily generating for $V$) and with coefficients in $C^1(U\times V)$; set

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_1(\mathit{\eta })(w,z)=\frac{(n-1)}{{(2\mathit{\pi }i)}^n}(\mathit{\eta }\wedge {({\overline{\mathit{\partial }}}_w\mathit{\eta })}^{n-2}\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta })(w,z)\end{array}$$

(4.10)

Note that ${\mathrm{\Omega }}_1(\mathit{\eta })(w,z)$ is of type $(n,n-2)$ in the variable $w$ and of type $(0,1)$ in the variable $z$. We call ${\mathrm{\Omega }}_1(\mathit{\eta })$ the Cauchy-Fantappie’ form of order 1 for$\mathit{\eta }$, and the previous one, ${\mathrm{\Omega }}_0(\mathit{\eta })$, will now be called Cauchy-Fantappie’ form of order 0.

In the previous properties $z$ was fixed; here it is allowed to vary.

Basic Property 3

We have (again for $\mathit{\eta }$ generating at $z$)

$$\begin{array}{c}\hfill {(2\mathit{\pi }i)}^n{\overline{\mathit{\partial }}}_z{\mathrm{\Omega }}_0(\mathit{\eta })(w,z)=-{({\overline{\mathit{\partial }}}_w\mathit{\eta })}^{n-1}\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta }+\mathit{\eta }\wedge {({\overline{\mathit{\partial }}}_w\mathit{\eta })}^{n-2}\wedge {\overline{\mathit{\partial }}}_z{\overline{\mathit{\partial }}}_w\mathit{\eta },\end{array}$$

(4.11)

For any $w\in U_z\cap U$, where $U_z$ is as in (4.2). Note that if the coefficients are in fact of class $C^2$ in each variable, then (4.11) has the equivalent formulation

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_z{\mathrm{\Omega }}_0(\mathit{\eta })(w,z)=-d_w{\mathrm{\Omega }}_1(\mathit{\eta })(w,z).\end{array}$$

(4.12)

Proof

As before, we specialize to the case: $n=2$ and leave the proof of the general case as an exercise for the reader. For $n=2$ identity (4.11) reads

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_z(\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_w\mathit{\eta })=-{\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta }+\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z{\overline{\mathit{\partial }}}_w\mathit{\eta }\end{array}$$

(4.13)

By the Leibniz rule we have

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_z(\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_w\mathit{\eta })={\overline{\mathit{\partial }}}_z\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_w\mathit{\eta }+\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z{\overline{\mathit{\partial }}}_w\mathit{\eta }\end{array}$$

and so it is clear that (4.13) will follow if we can show that

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta }=0,\text{for}\text{any}w\in U_z\end{array}$$

for any generating form $\mathit{\eta }$ with coefficients of class $C^1$. Proceeding as in the proof of basic property 2, we decompose

$$\begin{array}{c}\hfill U_z\cap U=U_z^1\cup U_z^2\end{array}$$

where $U_z^1$ and $U_z^2$ are as in (4.8) and (4.9), respectively. Again, we have

$$\begin{array}{c}\hfill {\mathit{\eta }}_1(w,z)(w_1-z_1)+{\mathit{\eta }}_2(w,z)(w_2-z_2)=1\text{for}\text{any}w\in U_z\end{array}$$

because $\mathit{\eta }$ is generating, and applying ${\overline{\mathit{\partial }}}_w$ to each side of this identity we find

$$\begin{array}{c}\hfill 0=\{\begin{array}{ccc}\left({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1\right)·(w_1-z_1)+\hfill & \left({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\right)·(w_2-z_2),\hfill & \text{if}w\in U_z^1\cap U_z^2\hfill \\ \hfill & \left({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1\right)·(w_1-z_1),\hfill & \text{if}w\in U_z^1\setminus U_z^2\hfill \\ \hfill & \left({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\right)·(w_2-z_2),\hfill & \text{if}w\in U_z^2\setminus U_z^1\hfill \end{array}\end{array}$$

(4.14)

Similarly, applying ${\overline{\mathit{\partial }}}_z$, we have

$$\begin{array}{c}\hfill 0=\{\begin{array}{ccc}\left({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_1\right)·(w_1-z_1)\hfill & +\left({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_2\right)·(w_2-z_2),\hfill & \text{if}w\in U_z^1\cap U_z^2\hfill \\ \hfill & \left({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_1\right)·(w_1-z_1),\hfill & \text{if}w\in U_z^1\setminus U_z^2\hfill \\ \hfill & \left({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_2\right)·(w_2-z_2),\hfill & \text{if}w\in U_z^2\setminus U_z^1\hfill \end{array}\end{array}$$

(4.15)

Now

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta }=({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1\wedge {\overline{\mathit{\partial }}}_z{\mathit{\eta }}_2-{\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\wedge {\overline{\mathit{\partial }}}_z{\mathit{\eta }}_1)\wedge {\mathit{dw}}_1\wedge {\mathit{dw}}_2\end{array}$$

(4.16)

Note that if $w\in U_z^1\setminus U_z^2$ then $w_1\ne z_1$, and so showing that

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta }=0\text{for}w\in U_z^1\setminus U_z^2\end{array}$$

is equivalent to showing that

$$\begin{array}{c}\hfill ({\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta })·(w_1-z_1)=0\end{array}$$

that is (using (4.16))

$$\begin{array}{c}\hfill ({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1·(w_1-z_1)\wedge {\overline{\mathit{\partial }}}_z{\mathit{\eta }}_2-{\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\wedge {\overline{\mathit{\partial }}}_z{\mathit{\eta }}_1·(w_1-z_1))\wedge {\mathit{dw}}_1\wedge {\mathit{dw}}_2=0\end{array}$$

but this is indeed true by the generating form hypothesis on $\mathit{\eta }$ as expressed in (4.14) and (4.15). This shows that the desired conclusion is true when $w\in U_z^1\setminus U_z^2$; the case: $w\in U_z^2\setminus U_z^1$ is dealt with in a similar fashion. Finally, if $w\in U_z^1\cap U_z^2$, then $(w_1-z_1)(w_2-z_2)\ne 0$ and

$$\begin{array}{cc}\hfill & ({\overline{\mathit{\partial }}}_w\mathit{\eta }\wedge {\overline{\mathit{\partial }}}_z\mathit{\eta })·(w_1-z_1)(w_2-z_2)\hfill \\ \hfill & =\left(\right({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_1)·(w_1-z_1)\wedge ({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_2)·(w_2-z_2)+\hfill \\ \hfill & -\left({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_2\right)·(w_2-z_2)\wedge \left({\overline{\mathit{\partial }}}_z{\mathit{\eta }}_1\right)·(w_1-z_1))\wedge {\mathit{dw}}_1\wedge {\mathit{dw}}_2\hfill \end{array}$$

but the two terms in the righthand side of this identity cancel out on account of (4.14) and (4.15). $\square$

5 Reproducing formulas: some general facts

In this section we highlight the theory of reproducing formulas for holomorphic functions by means of integral operators that arise from the Cauchy–Fantappié formalism. One of our goals here is to show that the usual reproducing properties of such operators extend to the situation where the data and the generating form have lower regularity. We begin with a rather specific example: the reproducing formula for the Bochner–Martinelli integral, see Proposition 1. The proof of this result is a consequence of a recasting of the classical mean value property for harmonic functions in terms of an identity (5.1) that links the Bochner-artinelli CF form on a sphere with the sphere’s Euclidean surface measure.

Because the Bochner–Martinelli integral of a continuous function is, in general, not holomorphic in $z$, in fact we need a more general version of Proposition 1 that applies to integral operators whose kernel is allowed to be any Cauchy–Fantappié form: this is done in Proposition 2.

While the operators defined so far are given by surface integrals over the boundary of the ambient domain, following an idea of Ligocka [26] another family of integral operators can be defined (essentially by ifferentiating the kernels of the operators in the statement of Proposition 2) which are realized as ‘solid” integrals over the ambient domain, and we show in Proposition 3 that such operators, too, have the reproducing property.

Lemma 1

Let $z\in {\mathbb{C}}^n$ be given and consider a ball centered at such $z$, ${\mathbb{B}}_r(z)=\{w\in {\mathbb{C}}^n,|w-z|<r\}$.

Then, at the center $z$ and for any $w\in \mathrm{b}{\mathbb{B}}_r(z)$ we have that the Bochner–Martinelli CF form for the ball ${\mathbb{B}}_r(z)$ has the following representation

$$\begin{array}{c}\hfill C_{\mathit{BM}}(w,z)=\frac{d\mathit{\sigma }(w)}{\mathit{\sigma }(\mathrm{b}{\mathbb{B}}_r(z))}\end{array}$$

(5.1)

where $d\mathit{\sigma }(w)$ is the element of Euclidean surface measure for $\mathrm{b}{\mathbb{B}}_r(z)$, and

$$\begin{array}{c}\hfill \mathit{\sigma }(\mathrm{b}{\mathbb{B}}_r(z))=\frac{2{\mathit{\pi }}^n{r}^{2n-1}}{(n-1)!}\end{array}$$

denotes surface measure of the sphere $\mathrm{b}{\mathbb{B}}_r(z)$.

Proof

We claim that the desired conclusion is a consequence of the following identity

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0({\mathit{\partial }}_w\mathit{\beta })(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n}\ast {\mathit{\partial }}_w\mathit{\beta }(w,z)\end{array}$$

(5.2)

where, as usual, we have set $\mathit{\beta }(w,z)=|w-z{|}^2$, and $\ast$ denotes the Hodge-star operator mapping forms of type $(p,q)$ to forms of type $(n-q,n-p)$. Let us first prove (5.1) assuming the truth of (5.2). To this end, we first note that from (5.2) and basic property 1 we have

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0\left(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}\right)(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n{\mathit{\beta }}^n}\ast {\mathit{\partial }}_w\mathit{\beta }(w,z),w\in {\mathbb{C}}^n.\end{array}$$

But ${\mathit{\partial }}_w\mathit{\beta }(w,z)=\mathit{\partial }\mathit{\rho }(w),$$w\in {\mathbb{C}}^n$ with $\mathit{\rho }(w):=\mathit{\beta }(w,z)-r^2$, a defining function for ${\mathbb{B}}_r(z)$. Now recall that $C_{\mathit{BM}}(w,z)=j^{\ast }{\mathrm{\Omega }}_0({\mathit{\partial }}_w\mathit{\beta }/\mathit{\beta })$ where $j$ is the inclusion: $\mathrm{b}{\mathbb{B}}_r(z)\hookrightarrow {\mathbb{C}}^n$, see Example 2, so that $j^{\ast }{\mathit{\beta }}^n=r^{2n}$. Combining these facts we conclude that, for $\mathit{\rho }$ as above

$$\begin{array}{c}\hfill C_{\mathit{BM}}(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n{r}^{2n}}{j}^{\ast }(\ast \mathit{\partial }\mathit{\rho })(w),w\in \mathrm{b}{\mathbb{B}}_r(z)\end{array}$$

and since $\parallel d\mathit{\rho }(w)\parallel =2r$ whenever $w\in \mathrm{b}{\mathbb{B}}_r(z)$, we obtain

$$\begin{array}{c}\hfill C_{\mathit{BM}}(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n{r}^{2n-1}}\frac{2j^{\ast }(\ast \mathit{\partial }\mathit{\rho })}{\parallel d\mathit{\rho }\parallel }(w),w\in \mathrm{b}{\mathbb{B}}_r(z);\end{array}$$

but

$$\begin{array}{c}\hfill d\mathit{\sigma }(w)=\frac{2j^{\ast }(\ast \mathit{\partial }\mathit{\rho })}{\parallel d\mathit{\rho }\parallel }(w),w\in \mathrm{b}{\mathbb{B}}_r(z)\end{array}$$

(5.3)

see [34, corollary III.3.5], and this gives (5.1).

We are left to prove (5.2): to this end, we assume $n=2$ and leave the case of arbitrary complex dimension as an exercise to for the reader. Since

$$\begin{array}{c}\hfill \ast {\mathit{dw}}_j=\frac{1}{2i^2}{\mathit{dw}}_j\wedge d{\overline{w}}_{j^{\prime }}\wedge {\mathit{dw}}_{j^{\prime }},\text{where}{j}^{\prime }=\{1,2\}\setminus \{j\}\end{array}$$

and

$$\begin{array}{c}\hfill {\mathit{\partial }}_w\mathit{\beta }=({\overline{w}}_1-{\overline{z}}_1){\mathit{dw}}_1+({\overline{w}}_2-{\overline{z}}_2){\mathit{dw}}_2\end{array}$$

then

$$\begin{array}{c}\hfill \ast {\mathit{\partial }}_w\mathit{\beta }=\frac{1}{2i^2}({\overline{w}}_1-{\overline{z}}_1){\mathit{dw}}_1\wedge d{\overline{w}}_2\wedge {\mathit{dw}}_2+({\overline{w}}_2-{\overline{z}}_2){\mathit{dw}}_2\wedge d{\overline{w}}_1\wedge {\mathit{dw}}_1\end{array}$$

On the other hand

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_w{\mathit{\partial }}_w\mathit{\beta }=d{\overline{w}}_1\wedge {\mathit{dw}}_1+d{\overline{w}}_2\wedge {\mathit{dw}}_2\end{array}$$

and so

$$\begin{array}{cc}\hfill {\mathrm{\Omega }}_0({\mathit{\partial }}_w\mathit{\beta })& =\frac{1}{{(2\mathit{\pi }i)}^2}{\mathit{\partial }}_w\mathit{\beta }\wedge {\overline{\mathit{\partial }}}_w{\mathit{\partial }}_w\mathit{\beta }\hfill \\ \hfill & =\frac{1}{{(2\mathit{\pi }i)}^2}(({\overline{w}}_1-{\overline{z}}_1){\mathit{dw}}_1\wedge d{\overline{w}}_2\wedge {\mathit{dw}}_2+({\overline{w}}_2-{\overline{z}}_2){\mathit{dw}}_2\wedge d{\overline{w}}_1\wedge {\mathit{dw}}_1)\hfill \\ \hfill & =\frac{1}{2{\mathit{\pi }}^2}\ast {\mathit{\partial }}_w\mathit{\beta }.\hfill \end{array}$$

This shows (5.2) and concludes the proof of the lemma.

(We remark in passing that identity (5.1), while valid for the Bochner–Martinelli generating form, is not true for general $\mathit{\eta }$.) $\square$

Definition 2

Given an integer $1\le k\le \infty$ and a bounded domain $D\subset {\mathbb{C}}^n$, we say that $D$is of class$C^k$ (alternatively, $D$ is $C^k$-smooth)if there is an open neighborhood $U$ of the boundary of $D$, and a real-valued function $\mathit{\rho }\in C^k(U)$ such that

$$\begin{array}{c}\hfill U\cap D=\{w\in U|\mathit{\rho }(w)<0\}\end{array}$$

and

$$\begin{array}{c}\hfill \nabla \mathit{\rho }(w)\ne 0\text{for}\text{any}w\in U.\end{array}$$

Any such function is called a defining function for$D$.

From this definition it follows that

$$\begin{array}{c}\hfill \mathrm{b}D=\{w\in U|\mathit{\rho }(w)=0\}\text{and}U\setminus \overline{D}=\{w\in U|\mathit{\rho }(w)>0\}.\end{array}$$

Proposition 1

For any bounded domain $V\subset {\mathbb{C}}^n$ with boundary of class $C^1$ and for any $f\in \mathit{\vartheta }(V)\cap C(\overline{V})$, we have

$$\begin{array}{c}\hfill f(z)={\mathbf{C}}_{\mathit{BM}}f(z),z\in V.\end{array}$$

Proof

Given $z\in V$, let $r>0$ be such that

$$\begin{array}{c}\hfill \overline{{\mathbb{B}}_{\mathbb{r}}(z)}\subset V.\end{array}$$

Note that the mean value property for harmonic functions:

$$\begin{array}{c}\hfill f(z)=\frac{1}{\mathit{\sigma }(\mathrm{b}{\mathbb{B}}_r(z))}\underset{\mathrm{b}{\mathbb{B}}_r(z)}{\int }f(w)d\mathit{\sigma }(w),f\in \text{Harm}({\mathbb{B}}_r(z))\cap C(\overline{{\mathbb{B}}_{\mathbb{r}}(z)})\end{array}$$

and identity (5.1) give

$$\begin{array}{c}\hfill f(z)=\underset{w\in \mathrm{b}{\mathbb{B}}_r(z)}{\int }f(w)C_{\mathit{BM}}(w,z)\end{array}$$

(5.4)

To prove the conclusion, we apply Stokes’ theorem on the set

$$\begin{array}{c}\hfill V_r(z):=V\setminus \overline{{\mathbb{B}}_{\mathbb{r}}(z)}\end{array}$$

and we obtain

$$\begin{array}{c}\hfill \underset{w\in V_r(z)}{\int }{d}_w(f(w){\mathrm{\Omega }}_0(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z)))=\underset{w\in {\mathit{bV}}_r(z)}{\int }f(w)C_{\mathit{BM}}(w,z)\end{array}$$

But by basic property 2, and since $f$ is holomorphic, we have

$$\begin{array}{c}\hfill d_w(f(w){\mathrm{\Omega }}_0(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z)))=f(w){\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_0(\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z))=0\end{array}$$

and so the previous identity becomes

$$\begin{array}{c}\hfill \underset{w\in \mathit{bV}}{\int }f(w)C_{\mathit{BM}}(w,z)=\underset{w\in b{\mathbb{B}}_r(z)}{\int }f(w)C_{\mathit{BM}}(w,z)\end{array}$$

but the lefthand side is ${\mathbf{C}}_{\mathit{BM}}f(z)$, while (5.4) says that the righthand side equals $f(z)$. $\square$

Proposition 2

Let $D\subset {\mathbb{C}}^n$ be a bounded domain of class $C^1$ and let $z\in D$ be given. Suppose that $\mathit{\eta }(·,z)$ is a generating form at $z$ relative to $D$. Suppose, furthermore, that the coefficients of $\mathit{\eta }(·,z)$ are in $C^1(U_z)$, where $U_z$ is as in Definition 1. Then, we have

$$\begin{array}{c}\hfill f(z)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left(\mathit{\eta }\right)(w,z)\text{for}\text{any}f\in \mathit{\vartheta }(D)\cap C(\overline{D}).\end{array}$$

(5.5)

Proof

Consider a smooth open neighborhood of $\mathrm{b}D$, which we denote $U_z(\mathrm{b}D)$, such that

$$\begin{array}{c}\hfill U_z(\mathrm{b}D)\subset U_z\end{array}$$

(5.6)

where $U_z$ is as in (4.1) and (4.2).Now fix two neighborhoods $U^{\prime }$ and $U^{\prime \prime }$ of the boundary of $D$ such that

$$\begin{array}{c}\hfill U^{\prime \prime }⋐U^{\prime }\subset U_z(\mathrm{b}D)\end{array}$$

and let ${\mathit{\chi }}_0(w,z)$ be a smooth cutoff function such that

$$\begin{array}{c}\hfill {\mathit{\chi }}_0(w,z)=\{\begin{array}{ccc}1\hfill & \text{if}\hfill & w\in U^{\prime \prime }\hfill \\ 0\hfill & \text{if}\hfill & w\in {\mathbb{C}}^n\setminus \overline{U^{\prime }}\hfill \end{array}\end{array}$$

(5.7)

Define

$$\begin{array}{c}\hfill {\mathit{\eta }}^{\circ }(w,z)={\mathit{\chi }}_0(w,z)\mathit{\eta }(w,z)+(1-{\mathit{\chi }}_0(w,z))\frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z)\end{array}$$

and

$$\begin{array}{c}\hfill D^{\circ }=D\cap U_z(\mathrm{b}D).\end{array}$$

Then ${\mathit{\eta }}^{\circ }$ is generating at $z$ relative to $D^{\circ }$ (and the open set $U_z$ of Definition 1 is the same for $\mathit{\eta }$ and for ${\mathit{\eta }}^{\circ }$); furthermore, it follows from (5.6) that

$$\begin{array}{c}\hfill \overline{D^{\circ }}\subset U_z.\end{array}$$

Now let $\{{\mathit{\eta }}_{\ell }^{\circ }{\}}_{\ell \in \mathbb{N}}$ be a sequence of $(1,0)$-forms with coefficients in $C^2(\overline{D^{\circ }})$ with the property that

$$\begin{array}{c}\hfill \parallel {\mathit{\eta }}_{\ell }^{\circ }-{\mathit{\eta }}^{\circ }(·,z){\parallel }_{C^1(\overline{D^{\circ }})}\to 0\text{as}\ell \to \infty .\end{array}$$

Suppose first that $f\in \mathit{\vartheta }(U(\overline{D}))$. Then by type considerations (and since $f$ is holomorphic in a neighborhood of $\overline{D}$) for any $w\in D^{\circ }$ and for any $\ell$ we have

$$\begin{array}{cc}\hfill d_w(f(w){\mathrm{\Omega }}_0({\mathit{\eta }}_{\ell }^{\circ })(w,z))& ={\overline{\mathit{\partial }}}_w(f(w){\mathrm{\Omega }}_0({\mathit{\eta }}_{\ell }^{\circ })(w,z))\hfill \\ \hfill & =f(w){\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_0({\mathit{\eta }}_{\ell }^{\circ })(w,z)=f(w){({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_{\ell }^{\circ })}^n(w,z)\hfill \end{array}$$

Thus, applying Stokes’ theorem on $D^{\circ }$ we find

$$\begin{array}{cc}\hfill & \underset{w\in D^{\circ }}{\int }f(w){({\overline{\mathit{\partial }}}_w{\mathit{\eta }}_{\ell }^{\circ })}^n(w,z)+\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}_{\ell }^{\circ }\right)(w,z)\hfill \\ \hfill & =\underset{w\in D\cap \mathrm{b}(U_z(\mathrm{b}D))}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}_{\ell }^{\circ }\right)(w,z)\hfill \end{array}$$

Letting $\ell \to \infty$ in the identity above we obtain

$$\begin{array}{cc}\hfill & \underset{w\in D^{\circ }}{\int }f(w){({\overline{\mathit{\partial }}}_w{\mathit{\eta }}^{\circ })}^n(w,z)+\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}^{\circ }\right)(w,z)\hfill \\ \hfill & =\underset{w\in D\cap \mathrm{b}(U_z(\mathrm{b}D))}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}^{\circ }\right)(w,z)\hfill \end{array}$$

Since ${\mathit{\eta }}^{\circ }$ is generating at $z$, by basic property 2 this expression is reduced to

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}^{\circ }\right)(w,z)=\underset{w\in D\cap \mathrm{b}(U_z(\mathrm{b}D))}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}^{\circ }\right)(w,z)\end{array}$$

(5.8)

But

$$\begin{array}{c}\hfill {\mathit{\eta }}^{\circ }(w,z)=\{\begin{array}{cc}\mathit{\eta }(w,z),\hfill & \text{for}w\text{in}\text{an}\text{open}\text{neighborhood}\text{of}\mathrm{b}D\hfill \\ \frac{{\mathit{\partial }}_w\mathit{\beta }}{\mathit{\beta }}(w,z),\hfill & \text{for}w\text{in}\text{an}\text{open}\text{neighborhood}\text{of}\mathrm{b}(U_z(\mathrm{b}D))\hfill \end{array}\end{array}$$

as a result, (5.8) reads

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left(\mathit{\eta }\right)(w,z)=\underset{w\in D\cap \mathrm{b}(U_z(\mathrm{b}D))}{\int }f(w)C_{\mathit{BM}}(w,z)\end{array}$$

On the other hand, $D\cap \mathrm{b}(U_z(\mathrm{b}D))=\mathrm{b}V$ for a (smooth) open set $V\subset D$, and using Proposition 1 we conclude that (5.5) holds in the case when $f\in \mathit{\vartheta }(U(\overline{D}))$. To prove the conclusion in the general case: $f\in \mathit{\vartheta }(D)\cap C(\overline{D})$, we write $D=\{\mathit{\rho }(w)<0\}$, so that $\mathit{\rho }(z)<0$ (since $z\in D$) and furthermore

$$\begin{array}{c}\hfill z\in D_k:=\left\{w\right|\mathit{\rho }(w)<-\frac{1}{k}\}\text{for}\text{any}k\ge k(z).\end{array}$$

(5.9)

But $D_k\subset D$ and so $f\in \mathit{\vartheta }(U({\overline{D}}_k))$; moreover

$$\begin{array}{c}\hfill \mathrm{b}{D}_k\subset U_z\text{for}k=k(z)\text{sufficiently}\text{large}.\end{array}$$

Thus, (5.5) grants

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}{D}_k}{\int }f(w)j_k^{\ast }{\mathrm{\Omega }}_0\left(\mathit{\eta }\right)(w,z)=f(z)\text{for}\text{any}k\ge k(z)\end{array}$$

where $j_k^{\ast }$ denotes the pullback under the inclusion $j_k:\mathrm{b}{D}_k\hookrightarrow {\mathbb{C}}^n$.

The conclusion now follows by letting $k\to \infty$. $\square$

We remark that in the case when $\mathit{\eta }$ is the Bochner–Martinelli generating form $\mathit{\eta }:={\mathit{\partial }}_w\mathit{\beta }/\mathit{\beta }$, Proposition 2 is simply a restatement of Proposition 1. However, since the coefficients of the Bochner–Martinelli CF form are nowhere holomorphic in the variable $z$, Proposition 1 is of limited use in the investigation of the Cauchy–Szegö and Bergman projections, and Proposition 2 will afford the use of more specialized choices of $\mathit{\eta }$.

The following reproducing formula is inspired by an idea of Ligocka [26].

Proposition 3

With same hypotheses as in Proposition 2, we have

$$\begin{array}{c}\hfill f(z)=\frac{1}{{(2\mathit{\pi }i)}^n}\underset{w\in D}{\int }f(w){({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z),f\in \mathit{\vartheta }(D)\cap L^1(D)\end{array}$$

for any $(1,0)$-form $\tilde{\mathit{\eta }}(·,z)$ with coefficients in $C^1(\overline{D})$ such that

$$\begin{array}{c}\hfill j^{\ast }{\mathrm{\Omega }}_0(\tilde{\mathit{\eta }})(·,z)=j^{\ast }{\mathrm{\Omega }}_0(\mathit{\eta })(·,z)\end{array}$$

(5.10)

where $j^{\ast }$ denotes the pullback under the inclusion $j:\mathrm{b}D\hookrightarrow {\mathbb{C}}^n$.

Note that if one further assumes that the coefficients of $\tilde{\mathit{\eta }}(·,z)$ are in $C^2(D)\cap C^1(\overline{D})$ then, as a consequence of the fact that $\overline{\mathit{\partial }}\circ \overline{\mathit{\partial }}=0$, we have

$$\begin{array}{c}\hfill \frac{1}{{(2\mathit{\pi }i)}^n}{({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n={\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_0(\tilde{\mathit{\eta }}).\end{array}$$

Proof

Fix $z\in D$ arbitrarily and let $\{{\tilde{\mathit{\eta }}}_{\ell }{\}}_{\ell \in \mathbb{N}}\subset C_{1,0}^2(\overline{D})$ be such that

$$\begin{array}{c}\hfill \parallel {\tilde{\mathit{\eta }}}_{\ell }-\tilde{\mathit{\eta }}(·,z){\parallel }_{C^1(\overline{D})}\to 0\text{as}\ell \to \infty .\end{array}$$

(5.11)

Suppose first that $f\in \mathit{\vartheta }(U(\overline{D}))$. Applying Stokes’ theorem to the $(n,n-1)$-form with coefficients in $C^1(\overline{D})$

$$\begin{array}{c}\hfill f·{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}_{\ell })\end{array}$$

we find

$$\begin{array}{c}\hfill \underset{w\in D}{\int }f(w)\overline{\mathit{\partial }}{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}_{\ell })(w)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}_{\ell })(w)\text{for}\text{any}\ell .\end{array}$$

On the other hand, since the coefficients of ${\tilde{\mathit{\eta }}}_{\ell }$ are in $C^2(D)$, we have

$$\begin{array}{c}\hfill \overline{\mathit{\partial }}{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}_{\ell })=\frac{1}{{(2\mathit{\pi }i)}^n}{(\overline{\mathit{\partial }}{\tilde{\mathit{\eta }}}_{\ell })}^n\text{for}\text{any}\ell \end{array}$$

and so the previous identity can be written as

$$\begin{array}{c}\hfill \frac{1}{{(2\mathit{\pi }i)}^n}\underset{w\in D}{\int }f(w){(\overline{\mathit{\partial }}{\tilde{\mathit{\eta }}}_{\ell })}^n(w)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}_{\ell })(w)\text{for}\text{any}\ell .\end{array}$$

Letting $\ell \to \infty$ in the identity above and using (5.11) we obtain

$$\begin{array}{c}\hfill \frac{1}{{(2\mathit{\pi }i)}^n}\underset{w\in D}{\int }f(w){(\overline{\mathit{\partial }}\tilde{\mathit{\eta }})}^n(w,z)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0(\tilde{\mathit{\eta }})(w,z).\end{array}$$

Combining the latter with the hypothesis (5.10) we obtain

$$\begin{array}{c}\hfill \frac{1}{{(2\mathit{\pi }i)}^n}\underset{w\in D}{\int }f(w){({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0(\mathit{\eta })(w,z)=f(z)\end{array}$$

where the last identity is due to Proposition 2.

If $f\in \mathit{\vartheta }(D)\cap L^1(D)$ then $f\in \mathit{\vartheta }(U({\overline{D}}_k))$, where $D_k$ is as in (5.9); moreover, $\mathrm{b}{D}_k\subset U_z\text{for}\text{any}k\ge k(z)$, so by the previous case we have

$$\begin{array}{c}\hfill f(z)=\underset{w\in D_k}{\int }f(w){({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z)\text{for}\text{any}k\ge k(z).\end{array}$$

The conclusion now follows by observing that

$$\begin{array}{c}\hfill \underset{w\in D_k}{\int }f(w){({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z)\to \underset{w\in D}{\int }f(w){({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z)\end{array}$$

as $k\to \infty$, by the Lebesgue dominated convergence theorem. $\square$

Note that the extension $\tilde{\mathit{\eta }}(w,z):={\mathit{\chi }}_0(w,z)\mathit{\eta }(w,z)$, with ${\mathit{\chi }}_0$ as in (5.7), satisfies a stronger condition than (5.10), namely the identity

$$\begin{array}{c}\hfill \tilde{\mathit{\eta }}(·,z)=\mathit{\eta }(·,z)\text{for}\text{any}w\in U_z^{\prime }(\mathrm{b}D).\end{array}$$

(5.12)

On the other hand, it will become clear in the sequel that this simple-minded extension is not an adequate tool for the investigation of the Bergman projection, and more ad-hoc constructions are presented in Sects. 7 and 9.

6 The role of pseudo-convexity

In order to obtain operators that satisfy the crucial condition (c) in Sect. 3 one would need generating forms whose coefficients are holomorphic. However, in contrast with the situation for the planar case (where the Cauchy kernel plays the role of a universal generating form with holomorphic coefficient) in higher dimension there is a large class of domains $V\subset {\mathbb{C}}^n$ that cannot support generating forms with holomorphic coefficients.¹ This dichotomy is related to the notion of domain of holomorphy, that is, the property that for any boundary point $w\in \mathrm{b}V$ there is a holomorphic function $f_w\in \mathit{\vartheta }(D)$ that cannot be continued holomorphically in a neighborhood of $w$. (Such notion is in turn equivalent to the notion of pseudo-convexity.) It is clear that every planar domain $V\subset \mathbb{C}$ is a domain of holomorphy, because in this case one may take $f_w(z):={(w-z)}^{-1}$ where $w\in \mathrm{b}V$ has been fixed. On the other hand the following

$$\begin{array}{c}\hfill V=\{z\in {\mathbb{C}}^2|1/2<|z|<1\}\end{array}$$

is a simple example of a smooth domain in ${\mathbb{C}}^2$ that is not a domain of holomorphy; other classical examples are discussed e.g., in [34, theorem II.1.1.]. A necessary condition for the existence of a generating form $\mathit{\eta }$ whose coefficients are holomorphic in the sense described above is then that $V$ be a domain of holomorphy. To prove the necessity of such condition, it suffices to observe that as a consequence of (4.2) and (4.1) one has

$$\begin{array}{c}\hfill \sum _{j=1}^n{\mathit{\eta }}_j(w,z)(w_j-z_j)=1\text{for}\text{any}w\in \mathrm{b}V,z\in V.\end{array}$$

(6.1)

It is now clear that for each fixed $w\in \mathrm{b}V$, at least one of the ${\mathit{\eta }}_j(w,z)$’s blows up as $z\to w$ (and it is well known that this is strong enough to ensure that $V$ be a domain of holomorphy).

In its current stage of development, the Cauchy–Fantappié framework is most effective in the analysis of two particular categories of pseudo-convex domains: these are the strongly pseudo-convex domains and the related category of strongly$\mathbb{C}$-linearly convex domains.

Definition 3

We say that a domain $D\subset {\mathbb{C}}^n$ is strongly pseudo-convex if $D$ is of class $C^2$ and if any defining function $\mathit{\rho }$ for $D$ satisfies the following inequality

$$\begin{array}{c}\hfill L_w(\mathit{\rho })(\mathit{\xi }):=\sum _{j,k=1}^n\frac{{\mathit{\partial }}^2\mathit{\rho }(w)}{\mathit{\partial }{\mathit{\zeta }}_j\mathit{\partial }{\overline{\mathit{\zeta }}}_k}{\mathit{\xi }}_j{\overline{\mathit{\xi }}}_k>0\text{for}\text{any}w\in \mathrm{b}D,\mathit{\xi }\in T_w^{\mathbb{C}}(\mathrm{b}D)\end{array}$$

(6.2)

where $T_w^{\mathbb{C}}$ denotes the complex tangent space to$\mathrm{b}D$at$w$, namely

$$\begin{array}{c}\hfill T_w^{\mathbb{C}}(\mathrm{b}D)=\{\mathit{\xi }\in {\mathbb{C}}^n|〈\mathit{\partial }\mathit{\rho }(w),\mathit{\xi }〉=0\},\end{array}$$

see [34, proposition II.2.14].

If $D$ is of class $C^k$ with $k\ge 1$, and if ${\mathit{\rho }}_1$ and ${\mathit{\rho }}_2$ are two distinct defining functions for $D$, it can be shown that there is a positive function $h$ of class $C^{k-1}$ in a neighborhood $U$ of the boundary of $D$, such that

$$\begin{array}{c}\hfill {\mathit{\rho }}_1(w)=h(w){\mathit{\rho }}_2(w),w\in U,\end{array}$$

and

$$\begin{array}{c}\hfill \nabla {\mathit{\rho }}_1(w)=h(w)\nabla {\mathit{\rho }}_2(w)\text{for}\text{any}w\in U\cap \mathrm{b}D,\end{array}$$

(6.3)

see [34, lemma II.2.5]. As a consequence of (6.3), if condition (6.2) is satisfied by one defining function then it will be satisfied by every defining function. The hermitian form $L_w(\mathit{\rho })$ defined by (6.2) is called the Levi form, or complex Hessian, of$\mathit{\rho }$ at $w$. We remark that in fact there is a “special” defining function $\mathit{\rho }$ for $D$ that is strictly plurisubharmonic on a neighborhood $U$ of $\overline{D}$, that is

$$\begin{array}{c}\hfill L_w(\mathit{\rho })(\mathit{\xi })>0\text{for}\text{any}w\in U\text{and}\text{any}\mathit{\xi }\in {\mathbb{C}}^n\setminus \{0\},\end{array}$$

(6.4)

see [34, proposition II.2.14], and we will assume throughout the sequel that $\mathit{\rho }$ satisfies this stronger condition.

We should point out that there is another notion of strong pseudo-convexity that includes the domains of Definition 3 as a subclass (this notion does not require the gradient of $\mathit{\rho }$ to be non-vanishing on $\mathrm{b}D$); within this more general context, the domains of Definition 3 are sometimes referred to as “strongly Levi-pseudo-convex”, see [34, §II.2.6 and II.2.8].

Definition 4

We say that $D\subset {\mathbb{C}}^n$ is strongly$\mathbb{C}$-linearly convex if $D$ is of class $C^1$ and if any defining function for $D$ satisfies this inequality:

$$\begin{array}{c}\hfill |〈\mathit{\partial }\mathit{\rho }(w),w-z〉|\ge C|w-z{|}^2\text{for}\text{any}w\in \mathrm{b}D,z\in \overline{D}.\end{array}$$

(6.5)

We we call those domains that satisfy the following, weaker condition

$$\begin{array}{c}\hfill |〈\mathit{\partial }\mathit{\rho }(w),w-z〉|>0\text{for}\text{any}w\in \mathrm{b}D\text{and}\text{any}z\in \overline{D}\setminus \{w\}\end{array}$$

(6.6)

strictly$\mathbb{C}$-linearly convex. This condition is related to certain separation properties of the domain from its complement by (real or complex) hyperplanes, see [1], [20, IV.4.6]: that this must be so is a consequence of the assertion that, for $w$ and $z$ as in (6.5), the quantity $|〈\mathit{\partial }\mathit{\rho }(w),w-z〉|$ is comparable to the Euclidean distance of $z$ to the complex tangent space $T_w^{\mathbb{C}}(\mathrm{b}D)$; we leave the verification of this assertion as an exercise for the reader.

It is not difficult to check that

$$\begin{array}{c}\hfill D:=\{z\in {\mathbb{C}}^n|\text{Im}{z}_n>{(|z_1{|}^2+\cdots +|z_{n-1}{|}^2)}^2\}\end{array}$$

is strictly, but not strongly, $\mathbb{C}$-linearly convex.

Lemma 2

If $D$ is strictly $\mathbb{C}$-linearly convex then for any $z\in D$ there is an open set $U_z\subset {\mathbb{C}}^n\setminus \{z\}$ such that $\mathrm{b}D\subset U_z$ and inequality (6.6) holds for any $w$ in $U_z$. Furthermore, if $D$ is strongly $\mathbb{C}$-linearly convex then the improved inequality (6.5) will hold for any $w\in U_z$.

Proof

Suppose that $D$ is strictly $\mathbb{C}$-linearly convex and fix $z\in D$. By the continuity of the function $h(\mathit{\zeta }):=|〈\mathit{\partial }\mathit{\rho }(\mathit{\zeta }),\mathit{\zeta }-z〉|$, if (6.6) holds at $w\in \mathrm{b}D$ then there is an open neighborhood $U_z(w)$ such that $h(\mathit{\zeta })>0$ for any $\mathit{\zeta }\in U_z(w)$ and so we have that $h(\mathit{\zeta })>0$ whenever

$$\begin{array}{c}\hfill \mathit{\zeta }\in U_z:=\bigcup _{w\in \mathrm{b}D}{U}_z(w).\end{array}$$

It is clear that $\mathrm{b}D\subset U_z$; furthermore, since $h(z)=0$ then $U_z(w)\subset {\mathbb{C}}^n\setminus \{z\}$ for any $w\in \mathrm{b}D$ and so $U_z\subset {\mathbb{C}}^n\setminus \{z\}$.

If $D$ is strongly $\mathbb{C}$-linearly convex then the conclusion will follow by considering the function $h(\mathit{\zeta }):=|〈\mathit{\partial }\mathit{\rho }(\mathit{\zeta }),\mathit{\zeta }-z〉|-C|\mathit{\zeta }-z{|}^2$. $\square$

Remark 1

We recall that in the classical definition of strong (resp. strict) convexity, the quantity $|〈\mathit{\partial }\mathit{\rho }(w),w-z〉|$ in the left-hand side of (6.5) (resp. (6.6)) is replaced by $\text{Re}〈\mathit{\partial }\mathit{\rho }(w),w-z〉$: it follows that any strongly (resp. strictly) convex domain is indeed strongly (resp. strictly) $\mathbb{C}$-linearly convex, but the converse is in general not true. It is clear that strongly (resp. strictly) convex domains satisfy a version of Lemma 2.

Lemma 3

Any strongly $\mathbb{C}$-linearly convex domain of class $C^2$ is strongly pseudo-convex.

The key point in the proof of this lemma is the observation that, as a consequence of (6.5), the real tangential Hessian of any defining function for a domain as in Lemma 3 is positive definite when restricted to the complex tangent space $T_w^{\mathbb{C}}(\mathrm{b}D)$ (viewed as a vector space over the real numbers). The converse of Lemma 3 is not true: we leave as an exercise for the reader to verify that the following (smooth) domain

$$\begin{array}{c}\hfill D:=\{z=(z_1,z_2)\in {\mathbb{C}}^2|\text{Im}{z}_2>2{(\text{Re}{z}_1)}^2-{(\text{Im}{z}_1)}^2\}\end{array}$$

is strongly pseudo-convex but not strongly $\mathbb{C}$-linearly convex.

In closing this section we remark that while the designations “strongly” and “strictly” indicate distinct families of $\mathbb{C}$-linearly convex domains (and of convex domains), for pseudo-convex domains there is no such distinction, and in fact in the literature the terms “strictly pseudo-convex” and “strongly pseudo-convex” are often interchanged: this is because the positivity condition (6.4) implies the seemingly stronger inequality

$$\begin{array}{c}\hfill L_w(\mathit{\rho },\mathit{\xi })\ge c_0|\mathit{\xi }{|}^2\text{for}\text{any}w\in U^{\prime }\text{and}\text{for}\text{any}\mathit{\xi }\in {\mathbb{C}}^n.\end{array}$$

(6.7)

Indeed, if (6.4) holds then the function $\mathit{\gamma }(w):=\min \{L_w(\mathit{\rho },\mathit{\xi })||\mathit{\xi }|=1\}$ is positive, and by bilinearity it follows that $L_w(\mathit{\rho },\mathit{\xi })\ge \mathit{\gamma }(w)|\mathit{\xi }{|}^2$ for any $\mathit{\xi }\in {\mathbb{C}}^n$; since $\mathit{\rho }$ is of class $C^2$ (and $D$ is bounded) we may further take the minimum of $\mathit{\gamma }(w)$ over, say, $w\in U^{\prime }\subset U$ and thus obtain (6.7), see [34, II.(2.26)].

7 Locally holomorphic kernels

A first step in the study of the Bergman and Cauchy–Szegö projections is the construction of integral operators with kernels given by Cauchy–Fantappié forms that are (at least) locally holomorphic in $z$, that is for $z$ in a neighborhood of each (fixed) $w$: it is at this juncture that the notion of strong pseudo-convexity takes center stage. In this section we show how to construct such operators in the case when $D$ is a bounded, strongly pseudo-convex domain, and we then proceed to prove the reproducing property.

To this end, we fix a strictly plurisubharmonic defining function for $D$; that is, we fix

$$\begin{array}{c}\hfill \mathit{\rho }:{\mathbb{C}}^n\to \mathbb{R},\mathit{\rho }\in C^2({\mathbb{C}}^n)\end{array}$$

such that $D=\{\mathit{\rho }<0\}$; $\nabla \mathit{\rho }(w)\ne 0$ for any $w\in \mathrm{b}D$ and

$$\begin{array}{c}\hfill L_w(\mathit{\rho },w-z)\ge 2c_0|w-z{|}^2,w,z\in {\mathbb{C}}^n\end{array}$$

where $L_w$ denotes the Levi form for $\mathit{\rho }$, see (6.2) and (6.7). Consider the Levi polynomial of$\mathit{\rho }$at$w$:

$$\begin{array}{c}\hfill \mathrm{\Delta }(w,z):=〈\mathit{\partial }\mathit{\rho }(w),w-z〉-\frac{1}{2}\sum _{j,k=1}^n\frac{{\mathit{\partial }}^2\mathit{\rho }(w)}{\mathit{\partial }{\mathit{\zeta }}_j\mathit{\partial }{\mathit{\zeta }}_k}(w_j-z_j)(w_k-z_k)\end{array}$$

Lemma 4

Suppose $D=\{\mathit{\rho }(w)<0\}$ is bounded and strongly pseudo-convex. Then, there is ${\widetilde{\mathit{ϵ}}}_0={\widetilde{\mathit{ϵ}}}_0(c_0)>0$ such that

$$\begin{array}{c}\hfill 2\mathrm{R}e\mathrm{\Delta }(w,z)\ge \mathit{\rho }(w)-\mathit{\rho }(z)+c_0|w-z{|}^2\end{array}$$

whenever $w\in D_{c_0}=\{w|\mathit{\rho }(w)<c_0\},$ and $z\in \overline{{\mathbb{B}}_{{\widetilde{\mathit{ϵ}}}_0}(w)}$.

Here $c_0$ is as in (7.1). We leave the proof of this lemma, along with the corollary below, as an exercise for the reader. Now let ${\mathit{\chi }}_1(w,z)$ be a smooth cutoff function such that

$$\begin{array}{c}\hfill {\mathit{\chi }}_1(w,z)=\{\begin{array}{ccc}1,\hfill & \text{if}\hfill & |w-z|<{\widetilde{\mathit{ϵ}}}_0/2\hfill \\ 0,\hfill & \text{if}\hfill & |w-z|>{\widetilde{\mathit{ϵ}}}_0\hfill \end{array}\end{array}$$

(7.1)

where ${\widetilde{\mathit{ϵ}}}_0$ is as in Lemma 4 and set

$$\begin{array}{c}\hfill g(w,z)={\mathit{\chi }}_1(w,z)\mathrm{\Delta }(w,z)+(1-{\mathit{\chi }}_1(w,z))|w-z{|}^2,w,z\in {\mathbb{C}}^n.\end{array}$$

(7.2)

Lemma 5

Suppose $D=\{\mathit{\rho }(w)<0\}$ is strongly pseudo-convex and of class $C^2$. Then, there is ${\tilde{\mathit{\delta }}}_0={\tilde{\mathit{\delta }}}_0({\widetilde{\mathit{ϵ}}}_0,c_0)>0$ such that

$$\begin{array}{c}\hfill 2\mathrm{R}eg(w,z)\ge \{\begin{array}{ccc}\mathit{\rho }(w)-\mathit{\rho }(z)+c_0|w-z{|}^2,\hfill & \mathrm{i}f\hfill & |w-z|\le {\widetilde{\mathit{ϵ}}}_0/2\hfill \\ \mathit{\rho }(w)+2{\tilde{\mathit{\delta }}}_0,\hfill & \mathrm{i}f\hfill & {\widetilde{\mathit{ϵ}}}_0/2\le |w-z|<{\widetilde{\mathit{ϵ}}}_0\hfill \\ {\widetilde{\mathit{ϵ}}}_0^2,\hfill & \mathrm{i}f\hfill & |w-z|>{\widetilde{\mathit{ϵ}}}_0\hfill \end{array}\end{array}$$

whenever

$$\begin{array}{c}\hfill w\in D_{c_0}=\{w|\mathit{\rho }(w)<c_0\}\end{array}$$

(7.3)

and

$$\begin{array}{c}\hfill z\in D_{2{\tilde{\mathit{\delta }}}_0}=\{w|\mathit{\rho }(w)<2{\tilde{\mathit{\delta }}}_0\}.\end{array}$$

Proof

It suffices to choose $0<{\tilde{\mathit{\delta }}}_0<c_0{\widetilde{\mathit{ϵ}}}_0^2/16$: the desired inequalities then follow from Lemma 4. $\square$

Corollary 1

Let $D=\{\mathit{\rho }(w)<0\}$ be a bounded, strongly pseudo-convex domain. Let

$$\begin{array}{c}\hfill {\mathrm{\Delta }}_j(w,z):=\frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }{\mathit{\zeta }}_j}(w)-\frac{1}{2}\sum _{k=1}^n\frac{{\mathit{\partial }}^2\mathit{\rho }(w)}{\mathit{\partial }{\mathit{\zeta }}_j\mathit{\partial }{\mathit{\zeta }}_k}(w_k-z_k),j=1,\dots ,n,\end{array}$$

Define

$$\begin{array}{c}\hfill {\mathit{\eta }}_j(w,z):=\frac{1}{g(w,z)}({\mathit{\chi }}_1(w,z){\mathrm{\Delta }}_j(w,z)+(1-{\mathit{\chi }}_1(w,z))({\overline{w}}_j-{\overline{z}}_j))\end{array}$$

where ${\mathit{\chi }}_1$ and $g$ are as in (7.1) and (7.2), and set

$$\begin{array}{c}\hfill \mathit{\eta }(w,z):=\sum _{j=1}^n{\mathit{\eta }}_j(w,z){\mathit{dw}}_j\text{for}(w,z)\in D_{c_0}\times D\end{array}$$

with $D_{c_0}$ as in (7.3). Then we have that $\mathit{\eta }(w,z)$ is a generating form for $D$, and one may take for $U_z$ in Definition 1 the set

$$\begin{array}{c}\hfill U_z:=\{w|\max \{\mathit{\rho }(z),-{\tilde{\mathit{\delta }}}_0\}<\mathit{\rho }(w)<\min \{|\mathit{\rho }(z)|,c_0\}\}.\end{array}$$

(7.4)

Note, however, that the coefficients of $\mathit{\eta }$ in this construction are only continuous in the variable $w$ and so the Cauchy–Fantappié form ${\mathrm{\Omega }}_0(\mathit{\eta })$ cannot be defined for such $\mathit{\eta }$ because doing so would require differentiating the coefficients of $\mathit{\eta }$ with respect to $w$, see (4.4). For this reason, proceeding as in [34], we refine the previous construction as follows. For ${\widetilde{\mathit{ϵ}}}_0$ as in Lemma 4 and for any $0<\mathit{ϵ}<{\widetilde{\mathit{ϵ}}}_0$, we let ${\mathit{\tau }}_{j,k}^{\mathit{ϵ}}\in C^{\infty }({\mathbb{C}}^n)$ be such that

$$\begin{array}{c}\hfill \underset{w\in \overline{D}}{\max }|\frac{{\mathit{\partial }}^2\mathit{\rho }(w)}{\mathit{\partial }{\mathit{\zeta }}_j\mathit{\partial }{\mathit{\zeta }}_k}-{\mathit{\tau }}_{j,k}^{\mathit{ϵ}}(w)|<\mathit{ϵ},j,k=1,\dots ,n\end{array}$$

We now define the following quantities:

$$\begin{array}{c}\hfill {\mathrm{\Delta }}_j^{\mathit{ϵ}}(w,z):=\frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }{\mathit{\zeta }}_j}(w)-\frac{1}{2}\sum _{k=1}^n{\mathit{\tau }}_{j,k}^{\mathit{ϵ}}(w)(w_k-z_k),j=1,\dots ,n;\end{array}$$

(7.5)

$$\begin{array}{c}\hfill {\mathrm{\Delta }}^{\mathit{ϵ}}(w,z):=\sum _{j=1}^n{\mathrm{\Delta }}_j^{\mathit{ϵ}}(w,z)(w_j-z_j);\end{array}$$

and, for ${\mathit{\chi }}_1$ as in (7.1):

$$\begin{array}{c}\hfill g^{\mathit{ϵ}}(w,z):={\mathit{\chi }}_1(w,z){\mathrm{\Delta }}^{\mathit{ϵ}}(w,z)+(1-{\mathit{\chi }}_1(w,z))|w-z{|}^2;\end{array}$$

(7.6)

$$\begin{array}{c}\hfill {\mathit{\eta }}_j^{\mathit{ϵ}}(w,z):=\frac{1}{g^{\mathit{ϵ}}(w,z)}({\mathit{\chi }}_1(w,z){\mathrm{\Delta }}_j^{\mathit{ϵ}}(w,z)+(1-{\mathit{\chi }}_1(w,z))({\overline{w}}_j-{\overline{z}}_j))\end{array}$$

and finally

$$\begin{array}{c}\hfill {\mathit{\eta }}^{\mathit{ϵ}}(w,z):=\sum _{j=1}^n{\mathit{\eta }}_j^{\mathit{ϵ}}(w,z){\mathit{dw}}_j.\end{array}$$

Lemma 6

Let $D=\{\mathit{\rho }(w)<0\}$ be a bounded strongly pseudo-convex domain. Then, there is ${\mathit{ϵ}}_0={\mathit{ϵ}}_0(c_0)>0$ such that for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ and for any $z\in D$, we have that ${\mathit{\eta }}^{\mathit{ϵ}}(w,z)$ defined as above is generating at $z$ relative to $D$ with an open set $U_z$ (see Definition 1) that does not depend on $\mathit{ϵ}$. Furthermore, we have that for each (fixed) $z\in D$ the coefficients of ${\mathit{\eta }}^{\mathit{ϵ}}(·,z)$ are in $C^1(U_z)$.

Proof

We first observe that ${\mathrm{\Delta }}^{\mathit{ϵ}}$ can be expressed in terms of the Levi polynomial $\mathrm{\Delta }$, as follows

$$\begin{array}{c}\hfill {\mathrm{\Delta }}^{\mathit{ϵ}}(w,z):=\mathrm{\Delta }(w,z)+\frac{1}{2}\sum _{j,k=1}^n(\frac{{\mathit{\partial }}^2\mathit{\rho }(w)}{\mathit{\partial }{\mathit{\zeta }}_j\mathit{\partial }{\mathit{\zeta }}_k}-{\mathit{\tau }}_{j,k}^{\mathit{ϵ}}(w))(w_j-z_j)(w_k-z_k)\end{array}$$

and so by Lemma 4 we have

$$\begin{array}{c}\hfill 2\mathrm{R}e{\mathrm{\Delta }}^{\mathit{ϵ}}(w,z)\ge \mathit{\rho }(w)-\mathit{\rho }(z)+c_0|w-z{|}^2\end{array}$$

for any

$$\begin{array}{c}\hfill 0<\mathit{ϵ}<{\mathit{ϵ}}_0:=\min \{{\widetilde{\mathit{ϵ}}}_0,2c_0/n^2\}\end{array}$$

whenever $w\in D_{c_0}=\{\mathit{\rho }(w)<c_0\}$ and $z\in \overline{{\mathbb{B}}_{{\mathit{ϵ}}_0}(w)}$. Proceeding as in the proof of Lemma 5 we then find that

$$\begin{array}{c}\hfill 2\mathrm{R}e{g}^{\mathit{ϵ}}(w,z)\ge \{\begin{array}{ccc}\mathit{\rho }(w)-\mathit{\rho }(z)+c_0|w-z{|}^2,\hfill & \mathrm{i}f\hfill & |w-z|\le {\mathit{ϵ}}_0/2\hfill \\ \mathit{\rho }(w)+{\mathit{\mu }}_0,\hfill & \mathrm{i}f\hfill & {\mathit{ϵ}}_0/2\le |w-z|<{\widetilde{\mathit{ϵ}}}_0\hfill \\ {\widetilde{\mathit{ϵ}}}_0^2,\hfill & \mathrm{i}f\hfill & |w-z|\ge {\widetilde{\mathit{ϵ}}}_0\hfill \end{array}\end{array}$$

for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ whenever

$$\begin{array}{c}\hfill w\in D_{c_0}=\{w|\mathit{\rho }(w)<c_0\}\end{array}$$

and

$$\begin{array}{c}\hfill z\in D_{{\mathit{\mu }}_0}=\{w|\mathit{\rho }(w)<{\mathit{\mu }}_0\}\end{array}$$

as soon as we choose

$$\begin{array}{c}\hfill 0<{\mathit{\mu }}_0<c_0{\mathit{ϵ}}_0^2/8.\end{array}$$

(7.7)

We then define the open set $U_z\subset {\mathbb{C}}^n\setminus \{z\}$ as in (7.4) but now with ${\mathit{\delta }}_0$ in place of ${\tilde{\mathit{\delta }}}_0$ (note that $U_z$ does not depend on $\mathit{ϵ}$). Then, proceeding as in the proof of corollary 1 we find that

$$\begin{array}{c}\hfill \underset{w\in U_z}{\inf }\text{Re}{g}^{\mathit{ϵ}}(w,z)>0\text{for}\text{any}0<\mathit{ϵ}<{\mathit{ϵ}}_0.\end{array}$$

From this it follows that ${\mathit{\eta }}^{\mathit{ϵ}}$ is a generating form for $D$; it is clear from (7.5) that the coefficients of ${\mathit{\eta }}^{\mathit{ϵ}}$ are in $C^1(U_z)$. $\square$

Lemma 6 shows that ${\mathit{\eta }}^{\mathit{ϵ}}$ satisfies the hypotheses of Proposition 2; as a consequence we obtain the following results:

Proposition 4

Let $D$ be a bounded strongly pseudo-convex domain. Then, for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ we have

$$\begin{array}{c}\hfill f(z)=\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_0\left({\mathit{\eta }}^{\mathit{ϵ}}\right)(w,z)\text{for}\text{any}f\in \mathit{\vartheta }(D)\cap C(\overline{D}),z\in D\end{array}$$

where ${\mathit{ϵ}}_0$ and ${\mathit{\eta }}^{\mathit{ϵ}}$ are as in Lemma 6.

Proposition 5

Let $D=\{\mathit{\rho }(w)<0\}$ be a bounded strongly pseudo-convex domain. Let

$$\begin{array}{c}\hfill {\tilde{\mathit{\eta }}}^{\mathit{ϵ}}(w,z):=\frac{g^{\mathit{ϵ}}(w,z)}{g^{\mathit{ϵ}}(w,z)-\mathit{\rho }(w)}{\mathit{\eta }}^{\mathit{ϵ}}(w,z),w\in \overline{D},z\in D.\end{array}$$

where ${\mathit{\eta }}^{\mathit{ϵ}}$ is as in Lemma 6. Then, for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ we have

$$\begin{array}{c}\hfill f(z)=\frac{1}{{(2\mathit{\pi }i)}^n}\underset{w\in D}{\int }f(w){({\overline{\mathit{\partial }}}_w{\tilde{\mathit{\eta }}}^{\mathit{ϵ}})}^n(w,z)\text{for}\text{any}f\in \mathit{\vartheta }(D)\cap L^1(D),z\in D.\end{array}$$

Proof

We claim that ${\tilde{\mathit{\eta }}}^{\mathit{ϵ}}$ satisfies the hypotheses of Proposition 3 for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$. Indeed, proceeding as in the proof of Lemma 6 we find that

$$\begin{array}{c}\hfill \text{Re}(g^{\mathit{ϵ}}(w,z)-\mathit{\rho }(w))>0\text{for}\text{any}w\in \overline{D},\text{for}\text{any}z\in D\end{array}$$

and for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$; from this it follows that

$$\begin{array}{c}\hfill {\tilde{\mathit{\eta }}}^{\mathit{ϵ}}(·,z)\in C_{1,0}^1(\overline{D})\text{for}\text{any}0<\mathit{ϵ}<{\mathit{ϵ}}_0.\end{array}$$

Moreover, as a consequence of basic property 1 we have

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}^{\mathit{ϵ}})(·,z)={\left(\frac{g^{\mathit{ϵ}}(·,z)}{g^{\mathit{ϵ}}(·,z)-\mathit{\rho }(·)}\right)}^n{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(·,z)\text{for}\text{any}0<\mathit{ϵ}<{\mathit{ϵ}}_0,\end{array}$$

but this grants

$$\begin{array}{c}\hfill j^{\ast }{\mathrm{\Omega }}_0({\tilde{\mathit{\eta }}}^{\mathit{ϵ}})(·,z)=j^{\ast }{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(·,z)\text{for}\text{any}0<\mathit{ϵ}<{\mathit{ϵ}}_0.\end{array}$$

The conclusion now follows from Proposition 3. $\square$

8 Correction terms

Propositions 4 and 5 have a fundamental limitation: it is that these propositions employ kernels, namely $j^{\ast }{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(w,z)$ and ${({\overline{\mathit{\partial }}}_w{\tilde{\mathit{\eta }}}^{\mathit{ϵ}})}^n(w,z)$, that are only locally holomorphic as functions of $z$, that is, they are holomorphic only for $z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$. In this section we address this issue by constructing for each of these kernels a “correction” term obtained by solving an ad-hoc $\overline{\mathit{\partial }}$-problem in the $z$-variable.

Throughout this section we shift our focus from the $w$-variable to $z$, that is: we fix $w\in \overline{D}$, we regard $z$ as a variable and we define the “parabolic” region

$$\begin{array}{c}\hfill {\mathcal{P}}_w:=\{z|\mathit{\rho }(z)+\mathit{\rho }(w)<c_0|w-z{|}^2\}.\end{array}$$

The region ${\mathcal{P}}_w$ has the following properties:

$$\begin{array}{cc}\hfill w& \in \overline{D}\Rightarrow D\subset {\mathcal{P}}_w;\hfill \\ \hfill w& \in \mathrm{b}D\Rightarrow z:=w\in \mathrm{b}{\mathcal{P}}_w.\hfill \end{array}$$

As a consequence of these properties we have that

$$\begin{array}{c}\hfill {\mathcal{P}}_w\cap {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)\ne \varnothing \end{array}$$

Lemma 7

Let $D=\{z|\mathit{\rho }(z)<0\}$ be a bounded strongly pseudo-convex domain. Then, there is ${\mathit{\mu }}_0={\mathit{\mu }}_0(c_0)>0$ such that

$$\begin{array}{c}\hfill D_{{\mathit{\mu }}_0}=\{z|\mathit{\rho }(z)<{\mathit{\mu }}_0\}\subset {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)\end{array}$$

(8.1)

for any (fixed) $w\in \overline{D}$. Furthermore, there is a bounded strongly pseudo-convex $\mathrm{\Omega }$ of class $C^{\infty }$ such that

$$\begin{array}{c}\hfill D_{{\mathit{\mu }}_0/2}=\{z|\mathit{\rho }(z)<{\mathit{\mu }}_0/2\}\subset \mathrm{\Omega }\subset D_{{\mathit{\mu }}_0}=\{z|\mathit{\rho }(z)<{\mathit{\mu }}_0\}\end{array}$$

where ${\mathit{\mu }}_0>0$ is as in (8.1).

Proof of Lemma 7

For the first conclusion, we claim that it suffices to choose ${\mathit{\mu }}_0={\mathit{\mu }}_0(c_0)$ as in (7.7). Indeed, given $z\in D_{{\mathit{\mu }}_0}$, if $|w-z|\ge {\mathit{ϵ}}_0/2$ then $\mathit{\rho }(z)\le c_0|w-z{|}^2/2$ and since $\mathit{\rho }(w)\le 0$ (as $w\in \overline{D}$) it follows that $z\in {\mathcal{P}}_w$. On the other hand, if $|w-z|<{\mathit{ϵ}}_0/2$ then of course $z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$.

To prove the second conclusion note that, since $\mathit{\rho }$ (the defining function of $D$) is of class $C^2$ and is strictly plurishubharmonic in a neighborhood of $\overline{D}$, there is $\tilde{\mathit{\rho }}\in C^{\infty }(U(\overline{D}))$ such that

$$\begin{array}{c}\hfill \parallel \tilde{\mathit{\rho }}-\mathit{\rho }{\parallel }_{C^2(U(\overline{D}))}\le {\mathit{\mu }}_0/8\end{array}$$

and

$$\begin{array}{c}\hfill L_z(\tilde{\mathit{\rho }},\mathit{\xi })>0\text{for}\text{any}z\in U^{\prime }(\overline{D})\text{and}\text{for}\text{any}\mathit{\xi }\in {\mathbb{C}}^n,\end{array}$$

see (6.2) and (6.4). Define

$$\begin{array}{c}\hfill \mathrm{\Omega }:=\left\{z\right|\tilde{\mathit{\rho }}(z)-\frac{3{\mathit{\mu }}_0}{4}<0\}\end{array}$$

Then $\mathrm{\Omega }$ is smooth and strongly pseudo-convex; we leave it as an exercise for the reader to verify that $\mathrm{\Omega }$ satisfies the desired inclusions: $D_{{\mathit{\mu }}_0/2}\subset \mathrm{\Omega }\subset D_{{\mathit{\mu }}_0}$. $\square$

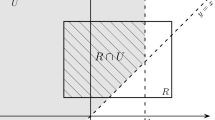
Lemma 7 shows that (the smooth and strongly pseudo-convex domain) $\mathrm{\Omega }$ has the following properties, see Fig. 1:

$$\begin{array}{c}\hfill \overline{D}\subset \mathrm{\Omega },\text{and}\overline{\mathrm{\Omega }}\subset {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w),\text{for}\text{every}w\in \overline{D}.\end{array}$$

We now set up two $\overline{\mathit{\partial }}$-problems on $\mathrm{\Omega }$. For the first $\overline{\mathit{\partial }}$-problem, we begin by observing that if $w$ is in $\mathrm{b}D$ and $z$ is in ${\mathcal{P}}_w$ then $\text{Re}{g}^{\mathit{ϵ}}(w,z)>0$ (that this must be so can be seen from the inequalities for Re $g^{\mathit{ϵ}}(w,z)$ that were obtained in the proof of Lemma 6), and so the coefficients of ${\mathit{\eta }}^{\mathit{ϵ}}(w,·)$ are in $C^{\infty }({\mathcal{P}}_w)$ whenever $w\in \mathrm{b}D$. Now fix $w\in \mathrm{b}D$ arbitrarily and denote by $H(w,z)=H_{\mathit{ϵ}}(w,z)$ the following double form, which is of type $(0,1)$ in $z$, and of type $(n,n-1)$ in $w$

$$\begin{array}{c}\hfill H(w,z)=\{\begin{array}{cc}-{\overline{\mathit{\partial }}}_z{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(w,z),\hfill & \text{if}z\in {\mathcal{P}}_w\hfill \\ 0,\hfill & \text{if}z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)\hfill \end{array}\end{array}$$

(8.2)

Now for each fixed $w\in \mathrm{b}D$, the coefficients of ${\mathrm{\Omega }}_0(w,z)$ are holomorphic in $z$ for $z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$ and so $H(w,z)$ is defined consistently in ${\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$. It is also clear that $H(w,z)$ is $C^{\infty }$ for $z\in {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$, and as such it depends continuously on $w\in \mathrm{b}D$. Moreover we have that ${\overline{\mathit{\partial }}}_{z}H(w,z)=0$, for $z\in {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w),w\in \mathrm{b}D$.

Fig. 1

The region ${\mathcal{P}}_w$ in the case when $w\in \mathrm{b}D$

For the second $\overline{\mathit{\partial }}$-problem, we begin by observing that if $w$ is in $\overline{D}$ and $z$ is in ${\mathcal{P}}_w$ then $\text{Re}(g^{\mathit{ϵ}}(w,z)-\mathit{\rho }(w))>0$ (that this must be so can again be seen from the inequalities for Re $g^{\mathit{ϵ}}(w,z)$ in the proof of Lemma 6), and so the coefficients of ${\tilde{\mathit{\eta }}}^{\mathit{ϵ}}(w,·)$ are in $C^{\infty }({\mathcal{P}}_w)$ whenever $w\in \overline{D}$. Fixing $w\in \overline{D}$ arbitrarily, we denote by $F(w,z)=F_{\mathit{ϵ}}(w,z)$ the following double form, which is of type $(0,1)$ in $z$, and of type $(n,n)$ in $w$

$$\begin{array}{c}\hfill F(w,z)=\{\begin{array}{cc}-{\overline{\mathit{\partial }}}_z{({\overline{\mathit{\partial }}}_w{\tilde{\mathit{\eta }}}^{\mathit{ϵ}})}^n(w,z),\hfill & \text{if}z\in {\mathcal{P}}_w\hfill \\ 0,\hfill & \text{if}z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)\hfill \end{array}\end{array}$$

Now for each fixed $w\in \overline{D}$, the coefficients of ${\tilde{\mathit{\eta }}}^{\mathit{ϵ}}(w,z)$ are holomorphic in $z$ for $z\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$ and so $F(w,z)$ is defined consistently in ${\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$. It is also clear that $F(w,z)$ is $C^{\infty }$ for $z\in {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$, and as such it depends continuously on $w\in \overline{D}$. Moreover we have that ${\overline{\mathit{\partial }}}_{z}F(w,z)=0$, for $z\in {\mathcal{P}}_w\cup {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w),w\in \overline{D}$.

Now let $\mathcal{S}={\mathcal{S}}_z$ be the solution operator, giving the normal solution of the problem $\overline{\mathit{\partial }}u=\mathit{\alpha }$ in $\mathrm{\Omega }$, via the $\overline{\mathit{\partial }}$-Neumann problem, so that $u=\mathcal{S}(\mathit{\alpha })$ satisfies the above whenever $\mathit{\alpha }$ is a $(0,1)$-form with $\overline{\mathit{\partial }}\mathit{\alpha }=0$. We set

$$\begin{array}{c}\hfill C_{\mathit{ϵ}}^2(w,z)={\mathcal{S}}_z(H(w,·)),w\in \mathrm{b}D\end{array}$$

(8.3)

and

$$\begin{array}{c}\hfill B_{\mathit{ϵ}}^2(w,z)={\mathcal{S}}_z(F(w,·)),w\in \overline{D}.\end{array}$$

Then by the regularity properties of $\mathcal{S}$, for which see e.g., [9, chapters 4 and 5], or [14], we have that $C_{\mathit{ϵ}}^2(w,z)$ is in $C^{\infty }(\overline{\mathrm{\Omega }})$, as a function of $z$, and is continuous for $w\in \mathrm{b}D$. Moreover ${\overline{\mathit{\partial }}}_z(C_{\mathit{ϵ}}^2(w,z))=-{\overline{\mathit{\partial }}}_z{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(w,z)=0$, for $z\in D$ (recall that $D\subset {\mathcal{P}}_w$) so

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_z({\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})+C_{\mathit{ϵ}}^2))(w,z)=0\text{for}z\in D\text{and}w\in \mathrm{b}D.\end{array}$$

We similarly have that $B_{\mathit{ϵ}}^2(w,z)$ is in $C^{\infty }(\overline{\mathrm{\Omega }})$, as a function of $z$, and is continuous for $w\in \overline{D}$ and, furthermore

$$\begin{array}{c}\hfill {\overline{\mathit{\partial }}}_z({({\overline{\mathit{\partial }}}_w{\tilde{\mathit{\eta }}}^{\mathit{ϵ}})}^n+B_{\mathit{ϵ}}^2))(w,z)=0\text{for}z\in D\text{and}w\in \overline{D}.\end{array}$$

9 Reproducing formulas: globally holomorphic kernels

At last, in this section we complete the construction of a number of integral operators that satisfy all three of the fundamental conditions (a)–(c) that were presented in Sect. 3. The crucial step in all these constructions is to produce integral kernels that are globally holomorphic in $D$ as functions of $z$. For strongly pseudo-convex domains, this goal is achieved by adding to each of the (locally holomorphic) Cauchy–Fantappié forms that were produced in Sect. 7 the ad-hoc “correction” term that was constructed in Sect. 8; the resulting two families of operators are denoted $\{{\mathbf{C}}_{\mathit{ϵ}}{\}}_{\mathit{ϵ}}$ (acting on $C(\mathrm{b}D)$) and $\{{\mathbf{B}}_{\mathit{ϵ}}{\}}_{\mathit{ϵ}}$ (acting on $L^1(D)$). In the case of strongly $\mathbb{C}$-linearly convex domains of class $C^2$, there is no need for “correction”: a natural, globally holomorphic Cauchy–Fantappié form is readily available that gives rise to an operator acting on $C(\mathrm{b}D)$ (even on $L^1(\mathrm{b}D)$), called the Cauchy–Leray Integral ${\mathbf{C}}_L$ and, in the more restrictive setting of strongly convex domains, also to an operator ${\mathbf{B}}_L$ that acts on $L^1(D)$. (As we shall see in Sect. 10, in the special case when the domain is the unit ball, the Cauchy–Leray integral ${\mathbf{C}}_L$ agrees with the Cauchy–Szegö projection $\mathbf{S}$, while the operator ${\mathbf{B}}_L$ agrees with the Bergman projection $\mathbf{B}$.) All the operators that are produced in this section satisfy, by their very construction, conditions (a) and (c) in Sect. 3, and we show in Propositions 6 through 9 that they also satisfy condition (b) (the reproducing property for holomorphic functions).

9.1 Strongly pseudo-convex domains

For ${\mathit{\eta }}_{\mathit{ϵ}}$ is as in Proposition 4 we now write

$$\begin{array}{c}\hfill C_{\mathit{ϵ}}^1(w,z)={\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(w,z)\end{array}$$

and let

$$\begin{array}{c}\hfill C_{\mathit{ϵ}}(w,z)=j^{\ast }(C_{\mathit{ϵ}}^1(w,z)+C_{\mathit{ϵ}}^2(w,z))\end{array}$$

and we define the operator

$$\begin{array}{c}\hfill {\mathbf{C}}_{\mathit{ϵ}}f(z)=\underset{w\in \mathrm{b}D}{\int }f(w)C_{\mathit{ϵ}}(w,z),z\in D,f\in C(\mathrm{b}D).\end{array}$$

(9.1)

Proposition 6

Let $D$ be a bounded strongly pseudo-convex domain. Then, for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ we have

$$\begin{array}{c}\hfill f(z)={\mathbf{C}}_{\mathit{ϵ}}f(z),\text{for}\text{any}f\in \mathit{\vartheta }(D)\cap C(\overline{D}),z\in D.\end{array}$$

Proof

By Proposition 4, for any $f\in \mathit{\vartheta }(D)\cap C(\overline{D})$ we have

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)C_{\mathit{ϵ}}(w,z)=f(z)+\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{C}_{\mathit{ϵ}}^2(w,z)\text{for}\text{any}z\in D,\end{array}$$

and so it suffices to show that

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{C}_{\mathit{ϵ}}^2(w,z)=0\text{for}\text{any}z\in D.\end{array}$$

By Fubini’s theorem and the definition of $C_{\mathit{ϵ}}^2$, see (8.3), we have

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{C}_{\mathit{ϵ}}^2(w,z)={\mathcal{S}}_z(\underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }H(w,·))\end{array}$$

where $H(w,·)$ is as in (8.2). Since the solution operator ${\mathcal{S}}_z$ is realized as a combinations of integrals over $\mathrm{\Omega }$ and $\mathrm{b}\mathrm{\Omega }$, the desired conclusion will be a consequence of the following claim:

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }H(w,\mathit{\zeta })=0\text{for}\text{any}\mathit{\zeta }\in \overline{\mathrm{\Omega }},\end{array}$$

and since $\overline{\mathrm{\Omega }}\subset {\mathcal{P}}_w$ for any $w\in \mathrm{b}D$, proving the latter amounts to showing that

$$\begin{array}{c}\hfill \underset{w\in M_{\mathit{\zeta }}}{\int }f(w)j^{\ast }{\overline{\mathit{\partial }}}_{\mathit{\zeta }}{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(w,\mathit{\zeta })=0\text{for}\text{any}\mathit{\zeta }\in \overline{\mathrm{\Omega }},\end{array}$$

(9.2)

where we have set

$$\begin{array}{c}\hfill M_{\mathit{\zeta }}=\{w\in \mathrm{b}D||w-\mathit{\zeta }|\ge {\mathit{ϵ}}_0/2\},\end{array}$$

(9.3)

see (8.2) and Fig. 2 below. To this end, we fix $\mathit{\zeta }\in \overline{\mathrm{\Omega }}$ arbitrarily; we claim that there is a sequence of forms ${({\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta }))}_{\ell }$ with the following properties:

• a. ${\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta })$ is generating at $\mathit{\zeta }$ relative to $D$;

• b. ${\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta })$ has coefficients in $C^2(U_{\mathit{\zeta }})$ with $U_{\mathit{\zeta }}$ as in Definition 1;

• c. as $\ell \to \infty$, we have that

  $$\begin{array}{c}\hfill j^{\ast }{\mathrm{\Omega }}_0({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(·,\mathit{\zeta })\to j^{\ast }{\mathrm{\Omega }}_0({\mathit{\eta }}^{\mathit{ϵ}})(·,\mathit{\zeta })\text{uniformly}\text{on}\mathrm{b}D;\end{array}$$

• d. the coefficients of ${\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })$ are holomorphic in $\mathit{\zeta }\in {\mathbb{B}}_{{\mathit{ϵ}}_0/2}(w)$ for any $w\in \mathrm{b}D$.

Note that (9.2) will follow from item c. above if we can prove that

$$\begin{array}{c}\hfill \underset{w\in M_{\mathit{\zeta }}}{\int }f(w)j^{\ast }{\overline{\mathit{\partial }}}_{\mathit{\zeta }}{\mathrm{\Omega }}_0({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })=0\text{for}\text{any}\ell .\end{array}$$

(9.4)

Fig. 2

The manifold $M_{\mathit{\zeta }}$ in the proof of Proposition 6

We postpone the construction of ${\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta })$ to later below, and instead proceed to proving (9.4) assuming the existence of the $\{{\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta }){\}}_{\ell }$. On account of items a. and b. above along with basic property 3 as stated in (4.12), proving (9.4) is equivalent to showing that

$$\begin{array}{c}\hfill \underset{w\in M_{\mathit{\zeta }}}{\int }f(w)j^{\ast }{\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })=0\text{for}\text{any}\ell .\end{array}$$

To this end, we first consider the case when $f\in \mathit{\vartheta }(D)\cap C^1(\overline{D})$, as in this case we have that

$$\begin{array}{c}\hfill f(w)j^{\ast }{\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })=j^{\ast }{\overline{\mathit{\partial }}}_w(f{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}}))(w,\mathit{\zeta })=j^{\ast }{d}_w(f{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}}))(w,\mathit{\zeta })\end{array}$$

(where in the last identity we have used the fact that ${\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_1=d_w{\mathrm{\Omega }}_1$ because ${\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})$ is of type $(n,n-2)$ in $w$). But the latter equals

$$\begin{array}{c}\hfill {\mathtt{d}}_w{j}^{\ast }(f{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}}))(w,\mathit{\zeta })\end{array}$$

where ${\mathtt{d}}_w$ denotes the exterior derivative operator for $M_{\mathit{\zeta }}$ viewed as a real manifold of dimension $2n-1$. Applying Stokes’ theorem on $M_{\mathit{\zeta }}$ to the form $\mathit{\alpha }(w):=j^{\ast }(f{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}}))(w,\mathit{\zeta })\in C_{n,n-2}^1(M_{\mathit{\zeta }})$ we obtain

$$\begin{array}{c}\hfill \underset{w\in M_{\mathit{\zeta }}}{\int }f(w)j^{\ast }{\overline{\mathit{\partial }}}_w{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })=\underset{w\in \mathrm{b}{M}_{\mathit{\zeta }}}{\int }f(w)j^{\ast }{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })\end{array}$$

but

$$\begin{array}{c}\hfill j^{\ast }{\mathrm{\Omega }}_1({\mathit{\eta }}_{\ell }^{\mathit{ϵ}})(w,\mathit{\zeta })=0\text{for}\text{any}w\in \mathrm{b}{M}_{\mathit{\zeta }}=\mathrm{b}D\cap \{|w-\mathit{\zeta }|={\mathit{ϵ}}_0/2\}\end{array}$$

because the coefficients of ${\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })$ are holomorphic in $\mathit{\zeta }\in {\mathbb{B}}_{\mathit{ϵ}/2}(w)$ for any $\mathrm{b}D$, see (4.10) and item d. above. This concludes the proof of Proposition 6 in the case when $f\in \mathit{\vartheta }(D)\cap C^1(\overline{D})$.

To prove the proposition in the case when $f\in \mathit{\vartheta }(D)\cap C^0(\overline{D})$, we fix $z\in D$ and choose $\mathit{\delta }=\mathit{\delta }(z)>0$ such that

$$\begin{array}{c}\hfill z\in D_{-\mathit{\delta }}=\{\mathit{\rho }<-\mathit{\delta }\}\mathrm{f}\mathrm{or}\mathrm{any}\mathit{\delta }\le \mathit{\delta }(z).\end{array}$$

Then we have that

$$\begin{array}{c}\hfill f\in \mathit{\vartheta }(D_{-\mathit{\delta }})\cap C^1({\overline{D}}_{-\mathit{\delta }})\mathrm{f}\mathrm{or}\mathrm{any}\mathit{\delta }\le \mathit{\delta }(z)\end{array}$$

and so by the previous argument we have

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}{D}_{-\mathit{\delta }}}{\int }f(w)j_{-\mathit{\delta }}^{\ast }{C}_{\mathit{ϵ}}^2(w,z)=0\mathrm{f}\mathrm{or}\mathrm{any}\mathit{\delta }\le \mathit{\delta }(z),\end{array}$$

(9.5)

where $j_{-\mathit{\delta }}^{\ast }$ denotes the pullback under the inclusion: $\mathrm{b}{D}_{-\mathit{\delta }}\hookrightarrow {\mathbb{C}}^n$. For $\mathit{\delta }$ sufficiently small there is a natural one-to-one and onto projection along the inner normal direction:

$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\delta }}:\mathrm{b}D\to \mathrm{b}{D}_{-\mathit{\delta }},\end{array}$$

and because $D$ is of class $C^2$ one can show that this projection tends in the $C^1$-norm to the identity ${\mathbf{1}}_{\mathrm{b}D}$, that is we have that

$$\begin{array}{c}\hfill \parallel {\mathbf{1}}_{\mathrm{b}D}-{\mathrm{\Lambda }}_{\mathit{\delta }}{\parallel }_{C^1(\mathrm{b}D)}\to 0\text{as}\mathit{\delta }\to 0.\end{array}$$

Using this projection one may then express the integral on $\mathrm{b}{D}_{-\mathit{\delta }}$ in identity (9.5) as an integral on $\mathrm{b}D$ for an integrand that now also depends on ${\mathrm{\Lambda }}_{\mathit{\delta }}$ and its Jacobian, and it follows from the above considerations that

$$\begin{array}{c}\hfill \underset{w\in \mathrm{b}{D}_{-\mathit{\delta }}}{\int }f(w)j_{-\mathit{\delta }}^{\ast }{C}_{\mathit{ϵ}}^2(w,z)\to \underset{w\in \mathrm{b}D}{\int }f(w)j^{\ast }{C}_{\mathit{ϵ}}^2(w,z)\text{as}\mathit{\delta }\to 0.\end{array}$$

We are left to construct, for each fixed $\mathit{\zeta }\in \overline{\mathrm{\Omega }}$, the sequence $\{{\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta }){\}}_{\ell }$ that was invoked earlier on. To this end, set

$$\begin{array}{c}\hfill U:=D\cup \bigcup _{z\in D}{U}_z\end{array}$$

where $U_z$ is the open neighborhood of $\mathrm{b}D$ that was determined in Lemma 6. Consider a sequence of real-valued functions $\{{\mathit{\rho }}_{\ell }{\}}_{\ell }\subset C^3({\mathbb{C}}^n)$ such that

$$\begin{array}{c}\hfill \parallel {\mathit{\rho }}_{\ell }-\mathit{\rho }{\parallel }_{C^1(U)}\to 0\text{as}\ell \to \infty ,\end{array}$$

and, for $\mathit{\zeta }\in \overline{\mathrm{\Omega }}$ fixed arbitrarily, set

$$\begin{array}{cc}\hfill {\mathrm{\Delta }}_{j,\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })& :=\frac{\mathit{\partial }{\mathit{\rho }}_{\ell }}{\mathit{\partial }{\mathit{\zeta }}_j}(w)-\frac{1}{2}\sum _{k=1}^n{\mathit{\tau }}_{j,k}^{\mathit{ϵ}}(w)(w_k-{\mathit{\zeta }}_k),j=1,\dots ,n;\hfill \\ \hfill {\mathrm{\Delta }}_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })& :=\sum _{j=1}^n{\mathrm{\Delta }}_{j,\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })(w_j-{\mathit{\zeta }}_j);\hfill \end{array}$$

and, for ${\mathit{\chi }}_1$ as in (7.1):

$$\begin{array}{cc}\hfill g_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })& :={\mathit{\chi }}_1(w,\mathit{\zeta }){\mathrm{\Delta }}_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })+(1-{\mathit{\chi }}_1(w,\mathit{\zeta }))|w-\mathit{\zeta }{|}^2;\hfill \\ \hfill {\mathit{\eta }}_{j,\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })& :=\frac{1}{g_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })}({\mathit{\chi }}_1(w,\mathit{\zeta }){\mathrm{\Delta }}_{j,\ell }^{\mathit{ϵ}}(w,\mathit{\zeta })+(1-{\mathit{\chi }}_1(w,\mathit{\zeta }))({\overline{w}}_j-{\overline{\mathit{\zeta }}}_j))\hfill \end{array}$$

and, finally

$$\begin{array}{c}\hfill {\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(w,\mathit{\zeta }):=\sum _{j=1}^n{\mathit{\eta }}_{j,\ell }^{\mathit{ϵ}}(w,\mathit{\zeta }){\mathit{dw}}_j,\end{array}$$

We leave it as an exercise for the reader to verify that $\{{\mathit{\eta }}_{\ell }^{\mathit{ϵ}}(·,\mathit{\zeta }){\}}_{\ell }$ has the desired properties. $\square$

Next, for ${\tilde{\mathit{\eta }}}^{\mathit{ϵ}}$ is as in Proposition 5, we write

$$\begin{array}{c}\hfill B_{\mathit{ϵ}}^1(w,z)=\frac{1}{{(2\mathit{\pi }i)}^n}{({\overline{\mathit{\partial }}}_w{\tilde{\mathit{\eta }}}^{\mathit{ϵ}})}^n\end{array}$$

and

$$\begin{array}{c}\hfill B_{\mathit{ϵ}}(w,z):=(B_{\mathit{ϵ}}^1+B_{\mathit{ϵ}}^2)(w,z),w\in \overline{D},z\in \overline{\mathrm{\Omega }},\end{array}$$

and we define the operator

$$\begin{array}{c}\hfill {\mathbf{B}}_{\mathit{ϵ}}f(z)=\underset{w\in D}{\int }f(w)B_{\mathit{ϵ}}(w,z),z\in D,f\in L^1(D).\end{array}$$

(9.6)

Proposition 7

Let $D$ be a bounded strongly pseudo-convex domain. Then, for any $0<\mathit{ϵ}<{\mathit{ϵ}}_0$ we have

$$\begin{array}{c}\hfill f(z)={\mathbf{B}}_{\mathit{ϵ}}f(z),\text{for}\text{any}f\in \mathit{\vartheta }(D)\cap L^1(D),z\in D.\end{array}$$

Proof

By Proposition 5, for any $f\in \mathit{\vartheta }(D)\cap L^1(D)$ we have

$$\begin{array}{c}\hfill \underset{w\in D}{\int }f(w)B_{\mathit{ϵ}}(w,z)=f(z)+\underset{w\in D}{\int }f(w)B_{\mathit{ϵ}}^2(w,z)\text{for}\text{any}z\in D,\end{array}$$

and so it suffices to show that

$$\begin{array}{c}\hfill \underset{w\in D}{\int }f(w)B_{\mathit{ϵ}}^2(w,z)=0\text{for}\text{any}z\in D.\end{array}$$

For the proof of this assertion we refer to [25, Proposition 3.2]. $\square$

9.2 Strictly $\mathbb{C}$-linearly convex domains: the Cauchy–Leray integral

Let $D$ be a bounded, strictly $\mathbb{C}$-linearly convex domain. We claim that if $\mathit{\rho }$ is (any) defining function for such a domain, and if $U$ is an open neighborhood of $\mathrm{b}D$ such that $\nabla \mathit{\rho }(w)\ne 0$ for any $w\in U$, then

$$\begin{array}{c}\hfill \mathit{\eta }(w,z):=\frac{\mathit{\partial }\mathit{\rho }(w)}{〈\mathit{\partial }\mathit{\rho }(w),w-z〉}\end{array}$$

(9.7)

is a generating form for $D$; indeed, by Lemma 2 for any $z\in D$ there is an open set $U_z\subset {\mathbb{C}}^n\setminus \{z\}$ such that $〈\mathit{\partial }\mathit{\rho }(w),w-z〉\ne 0$ for any $w\in U_z$ and $\mathrm{b}D\subset U_z$; thus the coefficients of $\mathit{\eta }(·,z)$ are in $C(U_z)$ and (4.1) holds. It is clear from (9.7) that $〈\mathit{\eta }(w,z),w-z〉=1$ for any $w\in U_z$, so (4.2) holds for any $z\in D$, as well. It follows that Proposition 2 applies to any strictly $\mathbb{C}$-linearly convex domain $D$ with $\mathit{\eta }$ chosen as above under the further assumption that $D$ be of class $C^2$ (which is required to ensure that the coefficients of $\mathit{\eta }(·,z)$ are in $C^1(U_z)$). The form

$$\begin{array}{c}\hfill C_L(w,z)=j^{\ast }{\mathrm{\Omega }}_0\left(\frac{\mathit{\partial }\mathit{\rho }(w)}{〈\mathit{\partial }\mathit{\rho }(w),w-z〉}\right)=j^{\ast }\left(\frac{\mathit{\partial }\mathit{\rho }(w)\wedge {(\overline{\mathit{\partial }}\mathit{\partial }\mathit{\rho })}^{n-1}(w)}{{(2\mathit{\pi }i〈\mathit{\partial }\mathit{\rho }(w),w-z〉)}^n}\right)\end{array}$$

(9.8)

is called the Cauchy–Leray kernel for$D$. It is clear that the coefficients of the Cauchy–Leray kernel are globally holomorphic with respect to $z\in D$: indeed the denominator $j^{\ast }〈\mathit{\partial }\mathit{\rho }(w),w-z{〉}^n$ is polynomial in the variable $z$, and by the strict $\mathbb{C}$-linear convexity of $D$ we have that $j^{\ast }〈\mathit{\partial }\mathit{\rho }(w),w-z{〉}^n\ne 0$ for any $z\in D$ and for any $w\in \mathrm{b}D$, see (6.6). The resulting integral operator:

$$\begin{array}{c}\hfill {\mathbf{C}}_{L}f(z)=\underset{w\in \mathrm{b}D}{\int }f(w)C_L(w,z)z\in D,\end{array}$$

(9.9)

is called the Cauchy–Leray Integral. Under the further assumption that $D$ be strictly convex (as opposed to strictly $\mathbb{C}$-linearly convex), for each fixed $z\in D$ one may extend $\mathit{\eta }(·,z)$ holomorphically to the interior of $D$ as follows

$$\begin{array}{c}\hfill \tilde{\mathit{\eta }}(·,z):=\left(\frac{〈\mathit{\partial }\mathit{\rho }(·),·-z〉}{〈\mathit{\partial }\mathit{\rho }(·),·-z〉-\mathit{\rho }(·)}\right)\mathit{\eta }(·,z)=\frac{\mathit{\partial }\mathit{\rho }(·)}{〈\mathit{\partial }\mathit{\rho }(·),·-z〉-\mathit{\rho }(·)}\end{array}$$

(9.10)

The following lemma shows that if $D$ is sufficiently smooth (again of class $C^2$) then $\tilde{\mathit{\eta }}$ satisfies the hypotheses of Proposition 3, and so in particular the operator

$$\begin{array}{c}\hfill {\mathbf{B}}_{L}f(z)=\underset{w\in D}{\int }f(w)B_L(w,z)\end{array}$$

with

$$\begin{array}{c}\hfill B_L(w,z)=\frac{1}{{(2\mathit{\pi }i)}^n}{({\overline{\mathit{\partial }}}_w\tilde{\mathit{\eta }})}^n(w,z)\end{array}$$

(9.11)

and $\tilde{\mathit{\eta }}$ given by (9.10), reproduces holomorphic functions.²

Lemma 8

If $D=\{\mathit{\rho }<0\}\subset {\mathbb{C}}^n$ is strictly convex and of class $C^2$, then for each fixed $z\in D$ we have that $\tilde{\mathit{\eta }}(·,z)$ given by (9.10) has coefficients in $C^1(\overline{D})$ and satisfies the hypotheses of Proposition 3.

Proof

In order to prove the first assertion it suffices to show that

$$\begin{array}{c}\hfill \text{Re}(〈\mathit{\partial }\mathit{\rho }(w),w-z〉)-\mathit{\rho }(w)>0\text{for}\text{any}w\in \overline{D},z\in D.\end{array}$$

(9.12)

Indeed, one first observes that if $D$ is strictly convex and sufficiently smooth then

$$\begin{array}{c}\hfill \text{Re}〈\mathit{\partial }\mathit{\rho }(w),w-z〉>0\text{for}\text{any}w\in \overline{D}\setminus \{z\}\end{array}$$

(see [20] for the proof of this fact) so that $\text{Re}〈\mathit{\partial }\mathit{\rho }(w),w-z〉$ is non-negative in $\overline{D}$ and it vanishes only at $w=z$. On the other other hand the term $-\mathit{\rho }(w)$ is non-negative for any $w\in \overline{D}$, and if $w=z\in D$ then $-\mathit{\rho }(w)=-\mathit{\rho }(z)>0$. This proves (9.12) and it follows that the coefficients of $\tilde{\mathit{\eta }}(·,z)$ are in $C^1(\overline{D})$. By basic property 1 we have

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_0(\tilde{\mathit{\eta }})(·,z)={\left(\frac{〈\mathit{\partial }\mathit{\rho }(·),·-z〉}{〈\mathit{\partial }\mathit{\rho }(·),·-z〉-\mathit{\rho }(·)}\right)}^n{\mathrm{\Omega }}_0(\mathit{\eta })(·,z);\end{array}$$

it is now immediate to verify that $j^{\ast }{\mathrm{\Omega }}_0(\tilde{\mathit{\eta }})(·,z)=j^{\ast }{\mathrm{\Omega }}_0(\mathit{\eta })(·,z),$ so that $\tilde{\mathit{\eta }}$ satisfies (5.10), as desired. $\square$

We summarize these results in the following two propositions:

Proposition 8

Suppose that $D$ is a bounded, strictly $\mathbb{C}$-linearly convex domain of class $C^2$. Then, with same notations as above we have

$$\begin{array}{c}\hfill f(z)={\mathbf{C}}_{L}f(z),z\in D,f\in \mathit{\vartheta }(D)\cap C(\overline{D}).\end{array}$$

Proposition 9

Suppose that $D$ is a bounded, strictly convex domain of class $C^2$. Then, with same notations as above we have that

$$\begin{array}{c}\hfill f(z)={\mathbf{B}}_{L}f(z),z\in D,f\in \mathit{\vartheta }(D)\cap L^1(D).\end{array}$$

10 $L^p$ estimates

In this section we discuss $L^p$-regularity of the Cauchy–Leray integral and of the Cauchy–Szegö and Bergman projections for the domains under consideration. Detailed proofs of the results concerning the Bergman projection, Theorem 3 and corollary 3 below, can be found in [25]. The statements concerning the Cauchy–Leray integral and the Cauchy–Szegö projection (Theorems 1 and 2 below,and Theorem 4 in the next section) are the subject of a series of forthcoming papers; here we will limit ourselves to presenting an outline of the main points of interest in their proofs.

We begin by recalling the defining properties of the Bergman and Cauchy–Szegö projections and of their corresponding function spaces.

10.1 The Bergman projection

Let $D\subset {\mathbb{C}}^n$ be a bounded connected open set.

Definition 5

For any $1\le q<\infty$ the Bergman space$\mathit{\vartheta }{L}^q(D)$ is

$$\begin{array}{c}\hfill \mathit{\vartheta }{L}^q(D)=\mathit{\vartheta }(D)\cap L^q(D,\mathit{dV}).\end{array}$$

The following inequality

$$\begin{array}{c}\hfill \underset{z\in \mathcal{K}}{\sup }|F(z)|\le C(\mathcal{K})\parallel F{\parallel }_{L^p(D,\mathit{dV})}\end{array}$$

which is valid for any compact subset $\mathcal{K}\subset D$ and for any holomorphic function $F\in \mathit{\vartheta }(D)$, shows that the Bergman space is a closed subspace of $L^q(D,\mathit{dV})$. This inequality also shows that the point evaluation:

$$\begin{array}{c}\hfill {\mathit{ev}}_z(f):=f(z),z\in D\end{array}$$

is a bounded linear functional on the Bergman space (take $\mathcal{K}:=\{z\}$). In the special case $q=2$, classical arguments from the theory of Hilbert spaces grant the existence of an orthogonal projection, called the Bergman projection for$D$

$$\begin{array}{c}\hfill \mathbf{B}:L^2(D)\to \mathit{\vartheta }{L}^2(D)\end{array}$$

that enjoys the following properties

$$\begin{array}{cc}\hfill & \mathbf{B}f(z)=f(z),f\in \mathit{\vartheta }{L}^2(D),z\in D\hfill \\ \hfill & {\mathbf{B}}^{\ast }=\mathbf{B}\hfill \\ \hfill & \parallel \mathbf{B}f{\parallel }_{L^2(D,\mathit{dV})}\le \parallel f{\parallel }_{L^2(D,\mathit{dV})},f\in L^2(D,\mathit{dV})\hfill \\ \hfill & \mathbf{B}f(z)=\underset{w\in D}{\int }f(w)\mathcal{B}(w,z)\mathit{dV}(w),z\in D,f\in L^2(D,\mathit{dV})\hfill \end{array}$$

where $\mathit{dV}$ denotes Lebesgue measure for ${\mathbb{C}}^n$. The function $\mathcal{B}(w,z)$ is holomorphic with respect to $z\in D$; it is called the Bergman kernel function. The Bergman kernel function depends on the domain and is known explicitly only for very special domains, such as the unit ball, see e.g. [35]:

$$\begin{array}{c}\hfill \mathcal{B}(w,z)=\frac{n!}{{\mathit{\pi }}^n{(1-[z,w])}^{n+1}},(w,z)\in {\mathbb{B}}_1(0)\times {\mathbb{B}}_1(0)\end{array}$$

(10.1)

here $[z,w]:=\sum _{j=1}^n{z}_j·{\overline{w}}_j$ is the hermitian product for ${\mathbb{C}}^n$.

10.2 The Cauchy–Szegö projection

Let $D\subset {\mathbb{C}}^n$ be a bounded connected open set with sufficiently smooth boundary. For such a domain, various notions of Hardy spaces of holomorphic functions can be obtained by considering (suitably interpreted) boundary values of functions that are holomorphic in $D$ and whose restriction to the boundary of $D$ has some integrability, see [36]. While a number of such definitions can be given, here we adopt the following

Definition 6

For any $1\le q<\infty$ the Hardy Space$H^q(\mathrm{b}D,d\mathit{\sigma })$ is the closure in $L^q(\mathrm{b}D,d\mathit{\sigma })$ of the restriction to the boundary of the functions holomorphic in a neighborhood of $\overline{D}$. In the special case when $q=2$ the orthogonal projection

$$\begin{array}{c}\hfill \mathbf{S}:L^2(\mathrm{b}D,d\mathit{\sigma })\to H^2(\mathrm{b}D,d\mathit{\sigma })\end{array}$$

is called the The Cauchy–Szegö Projection for$D$.

The Cauchy–Szegö projection has the following basic properties:

$$\begin{array}{cc}\hfill & {\mathbf{S}}^{\ast }=\mathbf{S}\hfill \\ \hfill & \parallel \mathbf{S}f{\parallel }_{L^2(\mathrm{b}D,d\mathit{\sigma })}\le \parallel f{\parallel }_{L^2(\mathrm{b}D,d\mathit{\sigma })},f\in L^2(\mathrm{b}D,d\mathit{\sigma })\hfill \\ \hfill & \mathbf{S}f(z)=\underset{w\in \mathrm{b}D}{\int }\mathcal{S}(w,z)f(w)d\mathit{\sigma }(w),z\in \mathrm{b}D.\hfill \end{array}$$

The function $\mathcal{S}(w,z)$, initially defined for $z\in \mathrm{b}D$, extends holomorphically to $z\in D$; it is called the Cauchy–Szegö kernel function. Like the Bergman kernel function, the Cauchy–Szegö kernel function depends on the domain $D$; for the unit ball we have [35]

$$\begin{array}{c}\hfill \mathcal{S}(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n{(1-[z,w])}^n},(w,z)\in \mathrm{b}{\mathbb{B}}_1(0)\times \mathrm{b}{\mathbb{B}}_1(0).\end{array}$$

(10.2)

10.3 $L^p$-estimates

We may now state our main results.

Theorem 1

Suppose $D$ is a bounded domain of class $C^2$ which is strongly $\mathbb{C}$-linearly convex. Then the Cauchy–Leray integral (9.9), initially defined for $f\in C^1(\mathrm{b}D)$, extends to a bounded operator on $L^p(\mathrm{b}D,d\mathit{\sigma })$, $1<p<\infty$.

It is only the weaker notion of strict  $\mathbb{C}$-linear convexity that is needed to define the Cauchy–Leray integral, but to prove the $L^p$ results one needs to assume strong$\mathbb{C}$-linear convexity.

Theorem 2

Under the assumption that the bounded domain $D$ has a $C^2$ boundary and is strongly pseudo-convex, one can assert that $\mathbf{S}$ extends to a bounded mapping on $L^p(\mathrm{b}D,d\mathit{\sigma })$, when $1<p<\infty$.

Theorem 3

Under the same assumptions on $D$ it follows that the operator $\mathbf{B}$ extends to a bounded operator on $L^p(D,\mathit{dV})$ for $1<p<\infty$.

The following additional results also hold.

Corollary 2

The result of Theorem 2 extends to the case when the projection $\mathbf{S}$ is replaced by the corresponding orthogonal projection ${\mathbf{S}}_{\mathit{\omega }}$, with respect to the Hilbert space $L^2(\mathrm{b}D,\mathit{\omega }d\mathit{\sigma })$ where $\mathit{\omega }$ is any continuous strictly positive function on $\mathrm{b}D$.

A similar variant of Theorem 3 holds for ${\mathbf{B}}_{\mathit{\omega }}$, the orthogonal projection on the sub-space of $L^2(D,\mathit{\omega }\mathit{dV})$. Here $\mathit{\omega }$ is any strictly positive continuous function on $\overline{D}$.

Corollary 3

One also has the $L^p$ boundedness of the operator $|B|$, whose kernel is $|\mathcal{B}(z,w)|\mathit{dV}(w)$, where $\mathcal{B}(z,w)$ is the Bergman kernel function.

10.4 Outline of the proofs

We begin by making the following remarks to clarify the background of these results.

• (1) The proofs of Theorems 2 and 3 make use of the whole family of operators $\{{\mathbf{C}}_{\mathit{ϵ}}{\}}_{\mathit{ϵ}}$, $0<\mathit{ϵ}<{\mathit{ϵ}}_0$: in order to obtain $L^p$ estimates for $p$ in the full range $(1,\infty )$ one needs the flexbility to choose $\mathit{ϵ}=\mathit{ϵ}(p)$ sufficiently small. (A single choice, as in [34], of ${\mathbf{C}}_{\mathit{ϵ}}$ for a fixed $\mathit{ϵ}$, will not do.)

• (2) There is no simple and direct relation between $\mathbf{S}$ and ${\mathbf{S}}_{\mathit{\omega }}$, nor between $\mathbf{B}$ and ${\mathbf{B}}_{\mathit{\omega }}$. Thus the results for general $\mathit{\omega }$ are not immediate consequences of the results for $\mathit{\omega }\equiv 1$.

• (3) When $\mathrm{b}D$ and $\mathit{\omega }$ are smooth (i.e. $C^k$ for sufficiently high $k$), the above results have been known for a long time (see e.g., the remarks that were made in Sect. 9 concerning the case when $D$ is the unit ball). Moreover when $\mathrm{b}D$ and $\mathit{\omega }$ are smooth (and $\mathrm{b}D$ is strongly pseudo-convex), there are analogous asymptotic formulas for the kernels in question due to [13], which allow a proof of Theorems 2 and 3 in these cases. See also [32].

• (4) Another approach to Theorem 3 in the case of smooth strongly pseudo-convex domains is via the $\overline{\mathit{\partial }}$-Neumann problem [9] and [14], but we shall not say anything more about this here.

A further point of interest is to work with the “Levi-Leray” measure $d{\mathit{\mu }}_{\mathit{\rho }}$ for the boundary of $D$, which we define as follows. We take the linear functional

$$\begin{array}{c}\hfill \ell (f)=\frac{1}{{(2\mathit{\pi }i)}^n}\underset{\mathrm{b}D}{\int }f(w)j^{\ast }(\mathit{\partial }\mathit{\rho }\wedge {(\overline{\mathit{\partial }}\mathit{\partial }\mathit{\rho })}^{n-1})\end{array}$$

(10.3)

and write $\ell f={\int }_{\mathrm{b}D}fd{\mathit{\mu }}_{\mathit{\rho }}$. We then have that $d{\mathit{\mu }}_{\mathit{\rho }}(w)=\mathcal{D}(w)d\mathit{\sigma }(w)$ where $\mathcal{D}(w)=c|\nabla \mathit{\rho }(w)|\det L_w(\mathit{\rho })$ via the calculation in [34] in the case $\mathit{\rho }$ is of class $C^2$, and we observe that $\mathcal{D}(w)\approx 1$, via (6.7).

With this we have that the Cauchy–Leray integral becomes

$$\begin{array}{c}\hfill {\mathbf{C}}_L(f)(z)=\underset{\mathrm{b}D}{\int }\frac{f(w)d{\mathit{\mu }}_{\mathit{\rho }}(w)}{〈\mathit{\partial }\mathit{\rho }(w),w-z{〉}^n}\end{array}$$

(10.4)

Thus the reason for isolating the measure $d{\mathit{\mu }}_{\mathit{\rho }}$ is that the coefficients of the kernel of each of ${\mathbf{C}}_L$ and its adjoint (computed with respect to $L^2(\mathrm{b}D,d{\mathit{\mu }}_{\mathit{\rho }})$), are $C^1$ functions in both variables. This would not be the case if we replaced $d{\mathit{\mu }}_{\mathit{\rho }}$ by the induced Lebesgue measure $d\mathit{\sigma }$ (and had taken the adjoint of ${\mathbf{C}}_L$ with respect to $L^2(\mathrm{b}D,d\mathit{\sigma })$).

In studying (10.4) we apply the “T(1)-theorem”technique [11], where the underlying geometry is determined by the quasi-metric

$$\begin{array}{c}\hfill |〈\mathit{\partial }\mathit{\rho }(w),w-z〉{|}^{\frac{1}{2}}\end{array}$$

(It is at this juncture that the notion of strong$\mathbb{C}$-linear convexity, as opposed to strict$\mathbb{C}$-linear convexity, is required.) In this metric, the ball centered at $w$ and reaching to $z$ has $d{\mathit{\mu }}_{\mathit{\rho }}$-measure $\approx |〈\mathit{\partial }\mathit{\rho }(w),w-z〉{|}^n$.

The study of (10.4) also requires that we verify cancellation properties in terms of its action on “bump functions.” These matters again differ from the case $n=1$, and in fact there is an unexpected favorable twist: the kernel in (10.4) is an appropriate derivative, as can be surmised by the observation that on the Heisenberg group one has ${(|z{|}^2+\mathit{it})}^{-n}=c^{\prime }\frac{d}{\mathit{dt}}{(|z{|}^2+\mathit{it})}^{-n+1},\text{if}n>1$. (However for $n=1$, the corresponding identity involves the logarithm!). Indeed by an integration-by-parts argument that is presented in (11.1) below, we see that when $n>1$ and $f$ is of class $C^1$,

$$\begin{array}{c}\hfill {\mathbf{C}}_L(f)(z)=c\underset{\mathrm{b}D}{\int }\frac{df(w)\wedge j^{\ast }{(\overline{\mathit{\partial }}\mathit{\partial }\mathit{\rho })}^{n-1}}{〈\mathit{\partial }\mathit{\rho }(w),w-z{〉}^{n-1}}+\mathbf{E}\mathbf{(}\mathbf{f}\mathbf{)}\mathbf{(}\mathbf{z}\mathbf{)},\end{array}$$

where

$$\begin{array}{c}\hfill \mathbf{E}\mathbf{(}\mathbf{f}\mathbf{)}\mathbf{(}\mathbf{z}\mathbf{)}=\underset{\mathrm{b}D}{\int }\mathcal{E}(z,w)f(w)d\mathit{\sigma }(w)\end{array}$$

with

$$\begin{array}{c}\hfill \mathcal{E}(z,w)=O(|z-w||〈\mathit{\partial }\mathit{\rho }(w),w-z〉{|}^{-n})\end{array}$$

so that the operator $\mathbf{E}$ is a negligible term.

A final point is that the hypotheses of Theorem 1 are in the nature of best possible. In fact, [4] gives examples of Reinhardt domains where the $L^2$ result for the Cauchy–Leray integral fails when a condition near $C^2$ is replaced by $C^{2-\mathit{ϵ}}$, or “strong” pseudo-convexity is replaced by its “weak” analogue.

One more observation concerning the Cauchy–Leray integral is in order. In the special case when $D$ is the unit ball ${\mathbb{B}}_1(0)$, we claim that the operators ${\mathbf{C}}_L$ and ${\mathbf{B}}_L$ agree, respectively, with the Cauchy–Szegö and Bergman projections for ${\mathbb{B}}_1(0)$. Indeed, for such domain the calculations in Sect. 9.2 apply with $U_z={\mathbb{C}}^n\setminus \{z\}$ and

$$\begin{array}{c}\hfill \mathit{\rho }(w):=|w{|}^2-1\end{array}$$

(10.5)

and by the Cauchy-Schwarz inequality we have $\text{Re}(〈\mathit{\partial }\mathit{\rho }(w),w-z〉)\ge |w|(|w|-|z|)\text{for}\text{any}w,z\in {\mathbb{C}}^n.$ Using (10.5) and (5.3)³ we find that

$$\begin{array}{c}\hfill C_L(w,z)=\frac{(n-1)!}{2{\mathit{\pi }}^n}\frac{d\mathit{\sigma }(w)}{{(1-[z,w])}^n}=\mathcal{S}(w,z)d\mathit{\sigma }\end{array}$$

which is the Cauchy–Szegö kernel for the ball, see (10.2) Next, we observe that, again for $D={\mathbb{B}}_1(0)$ and with $\mathit{\rho }$ as in (10.5), we have that

$$\begin{array}{c}\hfill 〈\mathit{\partial }\mathit{\rho }(w),w-z〉-\mathit{\rho }(w)=1-[z,w]\text{for}\text{any}w,z\in {\mathbb{C}}^n\end{array}$$

and from this it follows that (9.11) now reads

$$\begin{array}{c}\hfill B_L(w,z)=\frac{n!\mathit{dV}(w)}{{\mathit{\pi }}^n{(1-[z,w])}^{n+1}}=\mathcal{B}(w,z)\mathit{dV}(w)\end{array}$$

which is the Bergman kernel of the ball, see (10.1).

There are three main steps in the proof of Theorem 2.

• (i) Construction of a family of bounded Cauchy Fantappié-type integrals ${\mathbf{C}}_{\mathit{ϵ}}$

• (ii) Estimates for ${\mathbf{C}}_{\mathit{ϵ}}-{\mathbf{C}}_{\mathit{ϵ}}^{\ast }$

• (iii) Application of a variant of identity (2.1)

Step (i). The construction of ${\mathbf{C}}_{\mathit{ϵ}}$ was given in sections 7 through 9, see (9.1). One notes that the kernel $C_{\mathit{ϵ}}^2(w,z)$ of the correction term that was produced in Sect. 8 is “harmless” since it is bounded as $(w,z)$ ranges over $\mathrm{b}D\times \overline{D}$. Using a methodology similar to the proof of Theorem 1 one then shows

$$\begin{array}{c}\hfill \parallel {\mathbf{C}}_{\mathit{ϵ}}(f){\parallel }_{L^p}\le c_{\mathit{ϵ},p}\parallel f{\parallel }_{L^p},1<p<\infty .\end{array}$$

However it is important to point out, that in general the bound $c_{\mathit{ϵ},p}$ grows to infinity as $\mathit{ϵ}\to 0$, so that the ${\mathbf{C}}_{\mathit{ϵ}}$ can not be genuine approximations of $\mathbf{S}$. Nevertheless we shall see below that in a sense the ${\mathbf{C}}_{\mathit{ϵ}}$ gives us critical information about $\mathbf{S}$.

Step (ii). Here the goal is the following splitting:

Proposition 10

Given $0<\mathit{ϵ}<{\mathit{ϵ}}_0$, we can write

$$\begin{array}{c}\hfill {\mathbf{C}}_{\mathit{ϵ}}-{\mathbf{C}}_{\mathit{ϵ}}^{\ast }={\mathbf{A}}_{\mathit{ϵ}}+{\mathbf{R}}_{\mathit{ϵ}}\end{array}$$

where

$$\begin{array}{c}\hfill \parallel {\mathbf{A}}_{\mathit{ϵ}}{\parallel }_{L^p\to L^p}\le \mathit{ϵ}{c}_p,1<p<\infty \end{array}$$

(10.6)

and the operator ${\mathbf{R}}_{\mathit{ϵ}}$ has a bounded kernel, hence ${\mathbf{R}}_{\mathit{ϵ}}$ maps $L^1(\mathrm{b}D)$ to $L^{\infty }(\mathrm{b}D)$.

We note that in fact the bound of the kernel of ${\mathbf{R}}_{\mathit{ϵ}}$ may grow to infinity as $\mathit{ϵ}\to 0$.

To prove Proposition 10 we first verify an important “symmetry” condition: for each $\mathit{ϵ}$, there is a ${\mathit{\delta }}_{\mathit{ϵ}}$, so that

$$\begin{array}{c}\hfill |g^{\mathit{ϵ}}(w,z)-\overline{g^{\mathit{ϵ}}}(z,w)|\le \mathit{ϵ}c|w-z{|}^2,\text{if}|w-z|<{\mathit{\delta }}_{\mathit{ϵ}}.\end{array}$$

(10.7)

Here $g_{\mathit{ϵ}}(w,z)$ is as in (7.6). With this one proceeds as follows. Suppose $H_{\mathit{ϵ}}(z,w)$ is the kernel of the operator ${\mathbf{C}}_{\mathit{ϵ}}-{\mathbf{C}}_{\mathit{ϵ}}^{\ast }$. Then we take ${\mathbf{A}}_{\mathit{ϵ}}$ and ${\mathbf{R}}_{\mathit{ϵ}}$ to be the operators with kernels respectively ${\mathit{\chi }}_{\mathit{\delta }}(w-z)H_{\mathit{ϵ}}(w,z)$ and $(1-{\mathit{\chi }}_{\mathit{\delta }}(w-z))H_{\mathit{ϵ}}(w,z)$, where ${\mathit{\chi }}_{\mathit{\delta }}(w-z)$ is as in (7.6) and $\mathit{\delta }={\mathit{\delta }}_{\mathit{ϵ}}$, chosen acccording to (10.7).

Step (iii). We conclude the proof of Theorem 2 by using an identity similar to (2.1):

$$\begin{array}{c}\hfill \mathbf{S}(\mathbf{I}-({\mathbf{C}}_{\mathit{ϵ}}^{\ast }-{\mathbf{C}}_{\mathit{ϵ}}))={\mathbf{C}}_{\mathit{ϵ}}\end{array}$$

Hence

$$\begin{array}{c}\hfill \mathbf{S}(\mathbf{I}-{\mathbf{A}}_{\mathit{ϵ}})={\mathbf{C}}_{\mathit{ϵ}}+\mathbf{S}{\mathbf{R}}_{\mathit{ϵ}}\end{array}$$

Now for each $p$, take $\mathit{ϵ}>0$ so that for the bound $c_p$ as in (10.6)

$$\begin{array}{c}\hfill \mathit{ϵ}{c}_p\le \frac{1}{2}.\end{array}$$

Then $\mathbf{I}-{\mathbf{A}}_{\mathit{ϵ}}$ is invertible and we have

$$\begin{array}{c}\hfill \mathbf{S}=({\mathbf{C}}_{\mathit{ϵ}}+\mathbf{S}{\mathbf{R}}_{\mathit{ϵ}}){(\mathbf{I}-{\mathbf{A}}_{\mathit{ϵ}})}^{-1}\end{array}$$

Since ${(\mathbf{I}-{\mathbf{A}}_{\mathit{ϵ}})}^{-1}$ is bounded on $L^p$, and also ${\mathbf{C}}_{\mathit{ϵ}}$, it sufficies to see that $\mathbf{S}{\mathbf{R}}_{\mathit{ϵ}}$ is also bounded on $L^p$. Assume for the moment that $p\le 2$. Then since ${\mathbf{R}}_{\mathit{ϵ}}$ maps $L^1$ to $L^{\infty }$, it also maps $L^p$ to $L^2$ (this follows from the inclusions of Lebesgue spaces, which hold in this setting because $D$ is bounded), while $\mathbf{S}$ maps $L^2$ to itself, yielding the fact that $\mathbf{S}{\mathbf{R}}_{\mathit{ϵ}}$ is bounded on $L^p$. The case $2\le p$ is obtained by dualizing this argument.

The proof of Theorem 3 can be found in [25]: it has an outline similar to the proof of Theorem 2 with the operators ${\mathbf{B}}_{\mathit{ϵ}}$, see (9.6), now in place of the ${\mathbf{C}}_{\mathit{ϵ}}$, but the details are simpler since we are dealing with operators that converge absolutely (as suggested by corollary 3). Thus one can avoid the delicate $T(1)$-theorem machinery and make instead absolutely convergent integral estimates.

11 The Cauchy–Leray integral revisited

For domains with boundary regularity below the $C^2$ category there is no canonical notion of strong pseudo-convexity - much less a working analog of the Cauchy-type operators ${\mathbf{C}}_{\mathit{ϵ}}$ and ${\mathbf{B}}_{\mathit{ϵ}}$ that were introduced in the previous sections. By contrast, the Cauchy–Leray integral can be defined for less regular domains, but the definitions and the proofs are substantially more delicate than the $C^2$ framework of Theorem 1.

Definition 7

Given a bounded domain $D\subset {\mathbb{C}}^n$, we say that $D$is of class$C^{1,1}$ if $D$ has a defining function (in the sense of Definition 2) that is of class $C^{1,1}$ in a neighborhood $U$ of $\mathrm{b}D$; that is, $\mathit{\rho }$ is of class $C^1$ and its (real) partial derivatives $\mathit{\partial }\mathit{\rho }/\mathit{\partial }{x}_j$ are Lipschitz functions with respect to the Euclidean distance in ${\mathbb{C}}^n\equiv {\mathbb{R}}^{2n}$:

$$\begin{array}{c}\hfill |\frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }{x}_j}(w)-\frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }{x}_j}(\mathit{\zeta })|\le C|w-\mathit{\zeta }|w,\mathit{\zeta }\in U,j=1,\dots ,2n.\end{array}$$

Theorem 4

Suppose $D$ is a bounded domain of class $C^{1,1}$ which is strongly $\mathbb{C}$-linearly convex. Then there is a natural definition of the Cauchy–Leray integral (9.9), so that the mapping $f\mapsto {\mathbf{C}}_L(f)$ initially defined for $f\in C^1(\mathrm{b}D)$, extends to a bounded operator on $L^p(\mathrm{b}D,d\mathit{\sigma })$ for $1<p<\infty$.

Note that in comparison with Theorems 2 and 3, here our hypotheses about the nature of convexity are stronger, but the regularity of the boundary is weaker.

First, we explain the main difficulty in defining the Cauchy–Leray integral in the case of $C^{1,1}$ domains. It arises from the fact that the definitions (9.8) and (10.3) involve second derivatives of the defining function $\mathit{\rho }$. However $\mathit{\rho }$ is only assumed to be of class $C^{1,1}$, so that these derivatives are $L^{\infty }$ functions on ${\mathbb{C}}^n$, and as such not defined on $\mathrm{b}D$ which has 2$n$-dimensional Lebesgue measure zero. What gets us out of this quandary is that here in effect not all second derivatives are involved but only those that are “tangential” to $\mathrm{b}D$. Matters are made precise by the following “restriction” principle and its variants.

Suppose $F\in C^{1,1}({\mathbb{C}}^n)$ and we want to define $\overline{\mathit{\partial }}\mathit{\partial }F{|}_{\mathrm{b}D}$. We note that if $F$ were of class $C^2$ we would have

$$\begin{array}{c}\hfill \underset{\mathrm{b}D}{\int }{j}^{\ast }(\overline{\mathit{\partial }}\mathit{\partial }F)\wedge \mathrm{\Psi }=-\underset{\mathrm{b}D}{\int }{j}^{\ast }(\mathit{\partial }F)\wedge d\mathrm{\Psi },\end{array}$$

(11.1)

where $\mathrm{\Psi }$ is any $2n-3$ form of class $C^1$, and here $j^{\ast }$ is the induced mapping to forms on $\mathrm{b}D$.

Proposition 11

For $F\in C^{1,1}({\mathbb{C}}^n)$, there exists a unique 2-form $j^{\ast }(\overline{\mathit{\partial }}\mathit{\partial }F)$ in $\mathrm{b}D$ with $L^{\infty }(d\mathit{\sigma })$ coefficients so that (11.1) holds.

This is a consequence of an approximation lemma: There is a sequence $\{F_n\}$ of $C^{\infty }$ functions on ${\mathbb{C}}^n$, that are uniformly bounded in the $C^{1,1}({\mathbb{C}}^n)$ norm, so that $F_k\to F$ and $▿F_k\to ▿F$ uniformly on $\mathrm{b}D$, and moreover ${▿}_T^2{F}_n$ converges $(d\mathit{\sigma })$ a.e. on $\mathrm{b}D$. Here ${▿}_T^{2}F$ is the “tangential” restriction of the Hessian ${▿}^{2}F$ of $F$. Moreover the indicated limit, which we may designate as ${▿}_T^{2}F$, is independent of the approximating sequence $\{F_n\}$.