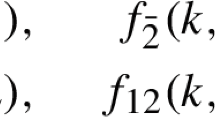Planar discrete isothermic nets of conical type

Abstract

We explore a specific discretization of isothermic nets in the plane which can also be interpreted as a discrete holomorphic map. The discrete orthogonality of the quadrilateral net is achieved by the so called conical condition imposed on vertex stars. That is, the sums of opposite angles between edges around all vertices are equal. This conical condition makes it possible to define a family of underlying circle patterns for which we can show invariance under Möbius transformations. Furthermore, we use the underlying circle pattern to characterize discrete isothermic nets in the projective model of Möbius geometry, and as Moutard nets in homogeneous coordinates in relation to the light cone in this model. We further investigate some examples of discrete isothermic nets and apply the Christoffel dual construction to obtain discrete minimal surfaces of conical type.

Appendix

In the appendix we give a proof of Proposition 2 with methods from classical projective geometry. We split up the proof into the following lemmas. For further details on projective geometry see e.g. the textbook [18].

Lemma 6

Let $\kappa :\mathbb {P}^2\rightarrow \mathbb {P}^2$ be a collineation in the real projective plane $\mathbb {P}^2$, and let g denote a straight line. Furthermore, let us denote the point of intersection of the line g and $\kappa (g)$ by s (see Fig. 13 left). Then the conic c that is tangent to all lines $a \vee \kappa (a)$ for all $a\in g$ (J. Steiner’s definition of line-conics) touches both lines g and $\kappa (g)$ at $\kappa ^{-1}(s)$ and $\kappa (s)$, respectively.

Proof

g and $\kappa (g)$ are in the set of lines tangent to c. Let us assume c touches g in a point t different from $\kappa ^{-1}(s)$. According to our definition of c the straight line h connecting t and $\kappa (t) \ne s$ is a tangent of c. However, it is impossible to have two different tangents g and h both going through t. The proof for $\kappa (s)$ being a contact point works analogously. $\square$

Fig. 13

Illustrations of Lemma 6 (left), Lemmas 7 and 8 (center), and proof of Proposition 2 (right)

Lemma 7

Let $f, f_i, f_{ij}, f_j\in \mathbb {P}^2$ be four points and let further $S_1, S_2$ be orientation preserving similarities defined by (for notation cf. Sect. 1.3 and Fig. 13 center)

$$\begin{aligned} S_1(f) = f_j,\quad S_1(f_i) = f_{ij},\quad \text {and}\quad S_2(f) = f_i,\quad S_2(f_j) = f_{ij}. \end{aligned}$$

Furthermore, let

$$\begin{aligned} f^-&= (f\vee f_i)\cap (f_j\vee f_{ij}),&f^+&= (f\vee f_j)\cap (f_i\vee f_{ij}),\\ f_{-j}^-&= S_1^{-1}(f^-),&f_{-i}^+&= S_2^{-1}(f^+),\\ f_{j}^-&= S_1(f^-),&f_{i}^+&= S_2(f^+). \end{aligned}$$

Then there is a conic c tangent

$$\begin{aligned} \text {to}\quad f\vee f_i&\quad \text {at}\quad f_{-j}^-,&\text {to}\quad f_j\vee f_{ij} \quad \text {at}\quad f_j^-,\end{aligned}$$

(6)

$$\begin{aligned} \text {to}\quad f\vee f_j&\quad \text {at}\quad f_{-i}^+,&\text {to}\quad f_i\vee f_{ij} \quad \text {at}\quad f_i^+. \end{aligned}$$

(7)

Proof

There is a conic c constructed with Lemma 6 for the collineation $\kappa = S_1$ and for $g = f \vee f_i$. Consequently, by construction (6) is fulfilled and the four connecting lines from (6) and (7) are tangent to c. Since $S_1$ is a similarity one tangent of c is the line at infinity. Consequently, c is the unique parabola tangent to the four lines from (6) and (7). Analogously, $S_2$ produces a parabola fulfilling (7) and having the same four tangents as c. Therefore the second conic is identically equal to c. $\square$

Lemma 8

We take the same assumptions and notations as in Lemma 7. Then the four lines

$$\begin{aligned} f_i \vee f_j, \quad f^- \vee f^+, \quad f_j^- \vee f_i^+, \quad f_{-j}^- \vee f_{-i}^+, \end{aligned}$$

all pass through a common point z. For an Illustration see Fig. 13 (center).

Proof

We apply Brianchon’s theorem (see e.g., [18, Th. 10.7]) two times.

First, we consider the two line elements (i.e., tangent plus contact point) $t_{12} = (f_j\vee f_{ij}, f_j^-)$, $t_{45} = (f_i\vee f_{ij}, f_i^+)$ and the two tangents $t_3 = f\vee f_j$ and $t_6 = f\vee f_i$. Brianchon’s theorem stays true if we replace two different tangents by one line element. That is, two tangents $t_1, t_2$ can be replaced by one line element $(t_{12}, T)$ where $t_1 \cap t_2$ then corresponds to the contact point T. Brianchon’s theorem now implies that the three lines

$$\begin{aligned} (t_1 \cap t_2) \vee (t_4 \cap t_5)&= f_j^- \vee f_i^+,\\ (t_2 \cap t_3) \vee (t_5 \cap t_6)&= f_j \vee f_i,\\ (t_3 \cap t_4) \vee (t_6 \cap t_1)&= f^+ \vee f^-, \end{aligned}$$

pass through a common point z. Analogously, for the two line elements $t_{12} = (f\vee f_{i}, f_{-j}^-)$, $t_{45} = (f\vee f_{j}, f_{-i}^+)$ and the two tangents $t_3 = f_i\vee f_{ij}$ and $t_6 = f_j\vee f_{ij}$ we obtain, by applying Brianchon’s theorem, that the three lines

$$\begin{aligned} (t_1 \cap t_2) \vee (t_4 \cap t_5)&= f_{-j}^- \vee f_{-i}^+,\\ (t_2 \cap t_3) \vee (t_5 \cap t_6)&= f_i \vee f_j,\\ (t_3 \cap t_4) \vee (t_6 \cap t_1)&= f^+ \vee f^-, \end{aligned}$$

pass through a common point ${\tilde{z}}$. However, z and ${\tilde{z}}$ is the same point since both lines $f_i\vee f_j$ and $f^+ \vee f^-$ are in both sets of lines. $\square$

Now we have collected all the properties we need to prove Proposition 2.

Proof of Proposition 2

By applying Pascals theorem (see e.g., [18, Th. 10.6]) we show the existence of a conic passing through $p_1 = f_{-i}^+$, $p_2 = f^+$, $p_3 = f_{i}^+$, $p_4 = f_{j}^-$, $p_5 = f^-$, $p_6 = f_{-j}^-$. Lemma 8 implies that the three points

$$\begin{aligned} (p_1 \vee p_2) \cap (p_4 \vee p_5) = f_j, \quad (p_2 \vee p_3) \cap (p_5 \vee p_6) = f_i, \quad (p_3 \vee p_4) \cap (p_6 \vee p_1) = z, \end{aligned}$$

are collinear (see Fig. 13 right). Consequently, Pascal’s theorem implies that the six points $p_1, \ldots , p_6$ lie on a conic. $\square$