Discussion on “Competition on Spatial Statistics for Large Datasets”

Abstract

We discuss the methods and results of the RESSTE team in the competition on spatial statistics for large datasets. In the first sub-competition, we implemented block approaches both for the estimation of the covariance parameters and for prediction using ordinary kriging. In the second sub-competition, a two-stage procedure was adopted. In the first stage, the marginal distribution is estimated neglecting spatial dependence, either according to the flexible Tuckey g and h distribution or nonparametrically. In the second stage, estimation of the covariance parameters and prediction are performed using Kriging. Vecchias’s approximation implemented in the GpGp package proved to be very efficient. We then make some propositions for future competitions.

1 Introduction

We congratulate the authors for organizing such a great and challenging competition. Our team brings together researchers from two French groups that have long-standing collaborations: the BioSP research unit at INRAE and the Geostatistics team at Mines ParisTech (formerly known as Ecole des Mines de Paris). They both belong to the RESSTE network¹ funded by INRAE. RESSTE organizes scientific animation around models, methods and algorithms for spatiotemporal data, and it fosters collaborations between statisticians and other scientists sharing interest in spatial and spatiotemporal data. Forced to be physically distant due to the Covid-19 sanitary crisis, we set up an efficient working environment with the help of collaborative online platforms for code, text and vivid discussions. We were thus able to contribute to all sub-competitions, including with multiple submissions for sub-competition 2. We enjoyed very much participating to this exercise. In addition to congratulate Huang, Sameh, Ying, Hatem, David and Marc for the excellent organization, we sincerely wish to thank them for the nice moments it brought to the four of us.

2 Competition 1: Block Approaches for Gaussian Processes

Data are known to have been generated from a Gaussian process with Matérn covariance function. Maximum likelihood (ML) would thus be the most efficient estimation method, and conditional expectation, also referred to as Kriging, is optimal for prediction. However, due to the size of the dataset, neither full ML nor unique neighborhood Kriging can be achieved, at the exception of ExaGeoStat. Efficient approximations must be sought. Here, we have opted for block approaches that satisfy the following principles: (i) in each block, estimation (ML) or prediction (Kriging) is optimal; (ii) blocks should be as large as possible while taking into account computational issues; (iii) blocks are assumed to be independent among each other. The approximation lies entirely in point (iii), and it is easy to understand that (ii) is the key for achieving good performances. What “large” means has slightly different meaning for estimation and for prediction. As regards estimation, some parameters control local properties, while others are global. Therefore, blocks for estimation need to have a large spatial extent. For plug-in Kriging, only local information is necessary. Prediction blocks are thus local, containing as many data points as possible. Details are provided below.

2.1 Estimation

First, a rough estimation of the parameters was performed on each dataset with weighted least squares fits for experimental variograms using the package RGeostats. These estimates, from which an approximate effective range $ER = {\hat{\beta }} \sqrt{12{\hat{\nu }}}$ was computed, allowed us to gain a general picture of the experimental design similar to that shown in Table 1 in Huang et al. (2021). In particular, ER was clearly close to the size of the domain for some datasets.

In a second stage, estimation of the parameters was performed using a maximum composite block-likelihood (BL) method. Blocks are characterized by their size (number of data points, $N_D$), shape and location of the data within the blocks. Nugget ($\tau ^2 \ge 0$) and smoothness ($\nu >0$) are local parameters, whilst range ($\beta >0$) and sill ($\sigma ^2 >0$) are non-local. When $\tau ^2=0$, Zhang (2004) showed that the only quantity that can be efficiently estimated in an in-fill asymptotic framework is $\sigma ^2 \beta ^{-2\nu }$. Efficient estimation of all parameters thus requires a “large domain” framework that allows sampling small distances for estimating $\tau ^2$ and $\nu$, and intermediate to large distances with respect to ER for estimating $\beta$ and $\sigma ^2$. In each block, the sub-sample must be built so as to sample all distances from 0 to a multiple of the practical range. Data separated by a distance larger than 2 to 3 times the practical range are useless for estimating nugget, regularity and range parameters and can be excluded. Here, blocks were disks with a radius set to 1.5ER, centered on a regular $B \times B$ grid covering the domain. $N_D$ points were then sampled at random within each disk with a weight decreasing linearly from the center (where it is equal to 1) to the edge of the disk (where it is equal to 0). After some experiments, the final setting was $B = 15$ and $N_D = 500$. For datasets G4/G12, when the smoothness parameter is large, the covariance matrix was seen as singular in R; in these cases, $N_D$ was set to 400. The function nlbmin was used for minimizing the negative log-BL. Initial values for the optimization were given by the WLS estimates of the first stage. Since blocks are random, this operation is repeated 5 times for each dataset. For each parameter, the average of the estimates was computed. This average is the final estimate.

2.2 Prediction

A “local unique neighborhood” technique is adopted, in which Kriging is performed at all locations belonging to the same block using a common neighborhood. To this end, a $K \times K$ regular grid is defined on the domain, and one Kriging system is built for each mesh of that grid, hereafter referred to as target block. The neighborhood of a given target block is a disk of radius $1.5\sqrt{2}/K$, so that all data belonging to the $3 \times 3$ meshes surrounding the center of the target block are part of the Kriging system. Smaller K yields higher precision but is computationally more demanding. Larger K leads to smaller neighborhood and lower precision. Computing time decreases rapidly as K increases, roughly at a $K^{-4}$ rate. A good trade-off between performance and speed was obtained with $K = 31$. The average number of training data per Kriging system was therefore around 1200.

2.3 Discussion

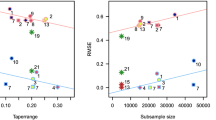
Overall these block approaches performed relatively well, ranking fourth and second in sub-competitions 1a and 1b, respectively. It is noticeable that in sub-competition 1b the plug-in block Kriging described above was only outperformed by ExaGeoStat using the true model, whereas ExaGeoStat with the estimated parameters performed slightly less well. As expected, we experienced some difficulties for the simultaneous estimation of $\beta$, $\nu$ and $\sigma ^2$ for smooth GPs with large effective range, i.e., when $\nu > 0.6$ and $ER > 0.1$. G4 is particularly poorly estimated, with simultaneous underestimation of the sill (${\hat{\sigma }}^2 =1.2092$) and underestimation of the range (${\hat{\beta }} = 0.0486$), resulting in a high MMOM and RMSE—even though MLOE is relatively small. Estimating $\nu$ when the regularity is high in the presence of a nugget is very challenging (G12, G13 and G15), as can be seen in Figures 2 and S1. In these cases, the poor estimation translated into high RMSEs for plug-in Kriging.

3 Competition 2: Trans-Gaussian Models

In this competition, the generating mechanism of the data was supposed to be unknown. Therefore, we first explored marginal distributions of the data using tools such as boxplots and histograms to check if a Gaussian model for the marginal distributions makes sense. If not, we followed the well-established statistical practice of using a marginally transformed Gaussian model. This approach, among which the Box–Cox transformation is the most popular representative, allows accommodating data features such as heavier-than-Gaussian tails or asymmetry of upper and lower tails.

3.1 Exploration of the Data

The first step of the solution to sub-competitions 2a and 2b is related to the exploratory analysis of the dataset. Some statistical quantities such as the mean, the minimum and maximum values (Table 1) were computed along with the histograms for each of the four datasets (Fig. 1a). It is clearly visible that only one of the four datasets (2b1) could be considered as marginally Gaussian distributed. The histograms of the other three datasets (2a1, 2a2, 2b2) present heavy tails toward high values. This fact is highlighted also by the maximal values of the datasets, which are extremely far from the mean if compared to the corresponding minimum values, showing asymmetry of tails. These insights suggest that the non-Gaussian datasets could be transformed to Gaussian models before applying geostatistical inference and prediction. Various types of transformations were inspected as reported in the next section.

Table 1 Mean, minimal and maximal value of the datasets of competition 2

Fig. 1

Histograms of the datasets of competition 2 with superimposed Gaussian density when adequate

3.2 Transformed Margins

3.2.1 Tukey g and h Transform

A flexible parametric marginal transform of Gaussian variables was proposed by J.W. Tukey and is known as the g and h distribution (Jorge and Boris 1984). It has been recently studied for spatial Gaussian fields by Xu and Genton (2017). Tukey g and h transformation function is strictly monotonic and defined as follows:

$$\begin{aligned} \tau _{g,h}(x) = {\left\{ \begin{array}{ll} \frac{1}{g}\left( \exp (gx)-1\right) \exp \left( hx^2/2\right) , &{} g\not =0,\\ x\exp \left( hx^2 /2\right) , &{} g=0, \end{array}\right. } \quad x\in {\mathbb {R}}, \quad h\ge , \ g\in {\mathbb {R}}. \end{aligned}$$

(1)

Given a standard Gaussian variable W, the Tukey g and h distribution is constructed as

$$\begin{aligned} Z=\beta _0 + \beta _1 \tau _{g,h}(W), \end{aligned}$$

with parameters to control location ($\beta _0$), scale ($\beta _1)$, asymmetry (g) and tail heaviness (h).

No external predictor variables were provided for the dataset, and visually we could not detect any other trends or anisotropies in the data. Therefore, we used a stationary and isotropic Tukey g and h random field model, which is obtained by applying the transformation (1) to a standard Gaussian random field with the Matérn covariance. We estimated the four parameters for each of the fields through the independence likelihood (neglecting spatial dependence) using the R library OpVaR; histograms of data after the inverse transformation to the standard Gaussian margins are shown in Figure 1b and correspond well to the superposed standard Gaussian density.

3.2.2 Nonparametric Transform

The estimation of the parameters of the Tukey g and h transform relies on an approximate parameter estimation procedure described below, which may conduct to underestimation or overestimation of the transformation parameters. Therefore, we also investigated the use of simple nonparametric transforms, namely a $\log$ transform for datasets 2a1 and 2b2 and a $\log$-$\log$ transform for dataset 2a2. Their adequacy was checked by a visual inspection of the histograms of the transformed data (not represented here), in particular their symmetry.

3.3 Estimation and Prediction

Joint estimation of marginal and dependence parameters can be useful to allow for transfer of information between the models for margins and dependence, and for very accurate assessment of uncertainty in estimates. However, two-step approaches with separate estimation of marginal parameters, followed by marginal transformation to the standard Gaussian scale and estimation of the Gaussian correlation function, have the advantage of being more robust. In particular, they allow for the combination of different estimation techniques for margins and dependence. We here adopt two-step approaches. In the first step, which is common to two of our three approaches, we implement two substeps: (1) estimation of the marginal parameters $\beta _0,\beta _1,g,h$ using the independence likelihood (i.e., by neglecting spatial dependence); (2) marginal transformation to the standard Gaussian scale using the parameters estimated in substep 1. In the last approach, we used a nonparametric transform. The following two subsections detail estimation after transformation of data to the standard Gaussian margins.

3.3.1 Bootstrap Approach

This approach is designed to run fast with moderate computing resources, such as those available on a personal computer. We proceed as follows using the pretransformed data:

• 1. Bootstrap estimations (25 samples) of Matérn correlation parameters using marginally pretransformed data: subsampling (without replacement) of 500 observations, and estimation of the scale and shape parameters of the Matérn correlation function.

• 2. The final estimated Matérn correlation parameters are set to the median of the bootstrap estimates.

• 3. Simple Kriging prediction is performed on the standard Gaussian scale by using k nearest neighbors of observed locations around the location to predict.

• 4. Standard Gaussian predictions are transformed back to the original scale by using the direct Tukey g and h transformation in (1) with parameters estimated in Step 1.

We have used validation data to choose among several values $k=25,50,100$ of nearest neighbors in Step 5. The implementation was realized using the R library CompRandFld for estimation of covariance parameters and Kriging.

3.3.2 GpGp

Vecchia approximations are a particular case of composite likelihood methods. They can also provide an approximation of the parent Gaussian process (Katzfuss and Guinness 2021). The computations are based on the Cholesky factor of the inverse covariance matrix that can be computed explicitly and that is sparse by construction. Therefore, they allow for numerically efficient inference and prediction. The package GpGp proposes an implementation of a Vecchia approximation that uses an elaborate way to order and group the data into conditionally independent blocks (Guinness 2018). It also provides an implementation of the Fisher scoring algorithm for the ML estimation of the parameters (Guinness 2021). We have used this package for parameter estimation and prediction for marginally pretransformed data in datasets 2a1, 2a2 and 2b2, or directly for dataset 2b1. Then, the predictions were transformed back into their original scale. The only parameter to be set is the number of neighbors to be considered in the groups for estimation and prediction. It has been set by trial and error regarding the prediction performances on out-of-sample validation data.

3.4 Validation

After transformation of the marginals (either through a nonparametric approach or through Tukey g and h), two parameters had to be set for the Vecchia approximation approach: the number of neighbors in the estimation step, $n_e$, and the number of neighbors in the prediction step, $n_p$. A holdout validation method was used to define the best $n_e$ and $n_p$. Each time 70000 (resp. 700000) data were selected as training points in the datasets of sub-competition 2a (resp. 2b), and RMSE was computed over the 20000 (resp. 200000) remaining points. The values of $n_e$ and $n_p$ leading to the best RMSE were $n_e=50$ for datasets in 2a, $n_e=30$ for datasets in 2b and $n_p=100$ for all datasets. In the bootstrap approach (Sect. 3.3.1), the size of the nearest neighbor Kriging neighborhood was set to 25 (Table 2).

Table 2 Submissions of the RESSTE team for competition 2

3.5 Discussion

Several methods were initially considered to treat the datasets of sub-competitions 2a and 2b, coming either from more classical geostatistical analyses or from machine learning techniques. Data-based methods such as random forests and neural networks, even when the spatial coordinates were combined with the addition of local features (mean/min/max values computed on K nearest neighbors), led to meager results in prediction.

Regarding competition 2, the type of point prediction to use depends on the score to be optimized. The conditional mean is known to minimize mean-squared error (MSE), and it corresponds to Kriging predictions. However, when marginal transformations are involved, the transformed conditional mean prediction is not equal to the conditional mean on the transformed scale. When the target is to minimize mean absolute errors, then conditional medians provide optimal predictions. With Gaussian data, conditional means and medians coincide. To compute conditional medians, we can simply transform data to the Gaussian scale, predict on the Gaussian scale, and then transform back to the original data scale. In competition 2, the target score was MSE. Due to very small prediction variances on the Gaussian scale, we found only very small differences between conditional median and conditional mean predictions on the non-Gaussian marginal scale of the original data. In some approaches (e.g., the bootstrap approach), we have therefore submitted marginally transformed Gaussian Kriging predictions.

4 Future Directions

This competition has explored different methods for the estimation of the parameters, and for the prediction (Kriging), of Gaussian and Tukey g and h trans-Gaussian random fields. Among these methods, several have achieved very good performance, as shown in Huang et al. (2021). More challenging setups than classical point data could also be considered, such as preferential sampling or the addition of location errors. An interesting question is whether the methods described in this paper would be efficient on gridded data, or whether grid-specific approaches would perform better. In particular, the case of gap filling (large areas without observations) could also be investigated.

Future competitions could also consider more challenging types of trans-Gaussian models arising in the analysis of agricultural, biological and environmental data, such as zero-inflated data, count data and other discrete data, or compositional data. Non-Gaussian margins arising from non (trans-)Gaussian random fields such as skew-Gaussian, skew-elliptical or max-stable random fields could also be considered.

Another very interesting extension would be to increase the dimensionality of the data by considering multivariate random fields, spatiotemporal random fields, or both. In different communities, such as machine learning, sensitivity analysis and uncertainty quantification, Gaussian processes are used in high-dimensional spaces. Testing the methods that have been developed successfully in spatial statistics to the problems faced by these communities offers interesting perspectives.

To provide a more realistic setting of real data analyses, future comparisons of prediction methods could also explore nonstationary settings with trend functions that may depend on external predictors, and with nonstationary covariance functions.