Introduction

Presently, convective heat transfer in nanofluids has wide range of applications, and plays a pivotal role in both sciences and engineering. They have many applications in almost every technology requiring heat transfer fluids (cooling or heating), solar energy, nuclear reactors, etc. So from the last few years the researchers of fluid dynamics are showing a keen interest in the study of nanofluids due to their applications in various fields. Heat, mass and momentum transfer over a stretching surface plays an important role in industries like polymer engineering, aerodynamics, wire drawing, stretching of plastic films, etc., as shown in the study by Altan et al. (1979). The boundary layer flow of a nanofluid past a stretching sheet was discussed by Makinde and Aziz (2011); in this study, they used convective boundary conditions to analyze the effects of physical parameters on the flow. Hady et al. (2012) have studied the radiation effect on viscous nanofluid over nonlinear stretching sheet using Runge–Kutta fourth-order technique. Heat and mass transfer of stagnation point flow over a stretching sheet in porous medium by considering heat source was discussed by Hamad and Ferdows (2012). The thermal conductivity of solid particles is several times more than that of the base or convectional fluids was concluded by Das et al. (2007) in the book nanofluids science and technology. Buongiorno (2006) presented different theories on the enhanced heat transfer characteristics of nanofluids and concluded that the thermal dispersion phenomenon cannot explain fully about the high heat transfer coefficients in nanofluids. The researchers Kumaran and Ramanaih (1996), Elbashbeshy (2001) proved that the stretching is not necessarily being linear and they extended their research on flow over a quadratic stretching sheet and nonlinearly stretching sheet, respectively. Rana and Bhargava (2012) used a finite element and finite difference methods for nonlinear stretching sheet problem. Effect of linear thermal stratification in stable stationary ambient fluid on steady MHD convective flow of a viscous incompressible fluid over a stretching sheet in presence of heat and mass transfer and magnetic field effect was discussed by Rushi Kumar (2013). A free convection MHD thermophoretic flow over an isothermal inclined plate was analyzed by Noor et al. (2012) and presented results for suction and injection cases. Kumari and Nath (2009) have proposed an analytical solution called homotopy analysis to discuss the unsteady MHD flow and heat transfer of a Newtonian fluid induced by an impulsively stretched plane. They used two lateral directions for this study. Ece (2005) has investigated the similarity analysis for the laminar-free convection boundary layer flow in the presence of a transverse magnetic field over a vertical down-pointing cone with mixed thermal boundary conditions. Many researchers like Oztop and Abu-Nada (2008), Mohan Krishna et al. (2014), Sandeep et al. (2013) have discussed the heat transfer characteristics of nanofluids by immersing the high-conductivity nanomaterials in the base fluids and concluded that the effective thermal conductivity of the fluid increases appreciably and consequently enhances the heat transfer characteristics by suspending the high thermal conductivity of nanomaterials in the base fluids. Prasad et al. (2010) considered viscoelastic fluid over a stretching sheet and analyzed the momentum and heat transfer characteristics of the boundary layers of an incompressible electrically conducting fluid. Andersson (1992) discussed the magnetohydrodynamic flow of a viscoelastic fluid over a stretching surface. A mathematical analysis to find the momentum and heat transfer characteristics of an incompressible, electrically conducting viscoelastic fluid over a linear stretching sheet was proposed by Abel et al. (2008). A clear investigation on nanofluid thermal properties was done by Philip et al. (2008). Wang and Mujumdar (2007) have given good literature on heat transfer characteristics of nanofluids.

In this study, we analyzed the effects of aligned magnetic field, thermal radiation, heat generation/absorption, cross-diffusion, viscous dissipation, heat source and chemical reaction on the flow of a nanofluid past an exponentially stretching sheet in porous medium. The governing partial differential equations are transformed to set of ordinary differential equations using self-similarity transformation, which are then solved numerically using bvp4c Matlab package. Finally the effects of various non-dimensional parameters on velocity, temperature, concentration, skin friction, local Nusselt and Sherwood numbers are thoroughly investigated and presented through graphs and tables.

Mathematical formulation

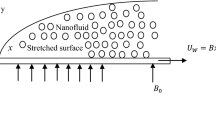
Consider a quiescent, incompressible, electrically conducting nanofluid in a porous medium past an impermeable vertical stretched sheet coinciding with the plane x = 0 and y axis is normal to the surface. An aligned magnetic field is applied in the y direction. Heat generation/absorption, radiation, viscous dissipation, chemical reaction and cross-diffusion effects are considered. The boundary layer equations that govern the present flow subject to the Boussinesq approximations can be expressed as

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{1}{{\rho_{\text{nf}} }}\left( {\mu_{\text{nf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} + \left( {\rho \beta } \right)_{\text{nf}} g(T - T_{\infty } ) + \left( {\rho \beta^{\prime } } \right)_{\text{nf}} g(C - C_{\infty } ) - \frac{{\mu_{\text{nf}} }}{k'}u - \sigma B^{2} (x)\sin^{2} \xi u} \right)$$
(2)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{\text{nf}} }}{{\left( {\rho c_{p} } \right)_{\text{nf}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \,\frac{{\upsilon_{f} }}{{\left( {c_{p} } \right)_{f} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} + \frac{{D_{m} K_{T} }}{{c_{s} c_{p} }}\frac{{\partial^{2} C}}{{\partial y^{2} }} - \,\,\frac{1}{{\left( {\rho c_{p} } \right)_{\text{nf}} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{Q_{0} }}{{\left( {\rho c_{p} } \right)_{\text{nf}} }}\left( {T - T_{\infty } } \right)$$
(3)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{m} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{m} K_{T} }}{{T_{m} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - K_{1} \left( {C - C_{\infty } } \right)$$
(4)

The boundary conditions of Eqs. (1)–(4) are

$$\begin{aligned} u = u_{w} ,\quad v = 0,\quad T = T_{w}, \quad C = C_{w} \,\,{\text{at}}\,\,y = 0 \hfill \\ u \to 0,\,\,\,\,T \to T_{\infty } ,\,\,\,C \to C_{\infty } \,\,\,\,{\text{as}}\,\,\,y \to \infty \hfill \\ \end{aligned}$$
(5)

where u and v are the velocity components in the x and y directions, respectively, T is the temperature, C is the concentration, \(T_{\infty }\) and \(C_{\infty }\) are the ambient temperature and concentration, respectively, \(\upsilon_{f}\) is the kinematic viscosity of the fluid, \(k^{\prime }\) is the permeability of porous medium, g is acceleration due to gravity, \(\mu_{\text{nf}}\) dynamic viscosity of the nanofluid, \(\left( {\rho \beta } \right)_{\text{nf}} ,\,\left( {\rho \beta^{\prime } } \right)_{\text{nf}}\) are the expansion coefficients thermal and concentration, respectively, \(B(x)\) is the applied magnetic field, \(\xi\) is the aligned angle, \(\rho_{\text{nf}}\) is nanofluid density, \(\sigma\) is electrical conductivity, \(k_{\text{nf}}\) is the thermal conductivity of nanofluid, \(\left( {c_{p} } \right)_{\text{nf}}\) is specific heat capacitance of nanofluid (see [16] for nano and base fluid relations), \(c_{s}\) is the concentration susceptibility. \(D_{m}\) is the mass diffusivity, \(K_{T}\) is the thermal diffusion ratio, \(T_{m}\) is the mean fluid temperature, \(K_{1}\) is the rate of chemical reaction.

Using Roseland approximation, the radiative heat flux \(q_{r}\) is given by

$$q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}$$
(6)

where \(\sigma^{*}\) is the Steffen Boltzmann constant and \(k^{*}\) is the mean absorption coefficient. Considering the temperature differences within the flow sufficiently small such that \(T^{4}\) may be expressed as the linear function of temperature, then expanding \(T^{4}\) in Taylor series about \(T_{\infty }\) and neglecting higher order terms takes the form

$$T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4}$$
(7)

In view of Eqs. (6) and (7), Eq. (3) reduces to

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{nf} }}{{\left( {\rho c_{p} } \right)_{\text{nf}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \,\frac{{\upsilon_{\text{nf}} }}{{\left( {c_{p} } \right)_{\text{nf}} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} + \frac{{D_{m} K_{T} }}{{\left( {c_{s} c_{p} } \right)_{f} }}\frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3\rho c_{p} k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{{\left( {\rho c_{p} } \right)_{\text{nf}} }}\left( {T - T_{\infty } } \right)$$
(8)

A similarity solution may be obtained by assuming the magnetic field term \(B(x)\) as of the form

$$B(x) = B_{0} e^{x/2l}$$
(9)

where \(B_{0}\) is the constant magnetic field. The similarity solutions of Eqs. (1)–(4) and (8) can be simplified by introducing the stream function \(\psi\) where

$$u = \frac{\partial \psi }{\partial y}\quad {\text{and}}\quad v = - \frac{\partial \psi }{\partial x}\,\,$$
(10)

With transformations

$$\psi = \sqrt{2Re\upsilon } e^{{{x \mathord{\left/ {\vphantom {x {2l}}} \right. \kern-0pt} {2l}}}} f(\eta ),\eta = \frac{y}{L}\sqrt{\frac{Re}{2}} e^{{{x \mathord{\left/ {\vphantom {x {2l}}} \right. \kern-0pt} {2l}}}} ,\,$$
$$\begin{aligned} &{{\left( {T - T_{\infty } } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{\infty } } \right)} {\left( {T_{w} - T_{\infty } } \right)}}} \right. \kern-0pt} {\left( {T_{w} - T_{\infty } } \right)}},\,\phi \left( \eta \right) = {{\left( {C - C_{\infty } } \right)} \mathord{\left/ {\vphantom {{\left( {C - C_{\infty } } \right)} {\left( {C_{w} - C_{\infty } } \right)}}} \right. \kern-0pt} {\left( {C_{w} - C_{\infty } } \right)}}, \hfill \\ &T - T_{\infty } = T_{0} e^{2x/l} \theta (\eta ),C - C_{\infty } = C_{0} e^{2x/l} \phi (\eta ) \hfill \\ \end{aligned}$$
(11)

Substituting (9) and (11) in the governing equations gives

$$f^{\prime \prime \prime } + ff^{\prime \prime } - 2f^{\prime 2} + 2\tau \left( {\theta + N_{1} \phi } \right) - \left( {M\sin^{2} \xi + \frac{1}{K}} \right)f^{\prime } = 0$$
(12)
$$\frac{1}{\Pr }\left( {\frac{3 + 4R}{3}} \right)\theta^{\prime \prime } + f\theta^{\prime } - \left( {4f^{\prime } - Q} \right)\theta + Ec\left( {f^{\prime \prime } } \right)^{2} + \;D_{f} \phi^{\prime \prime } = 0$$
(13)
$$\frac{1}{Sc}\phi^{\prime \prime } + f\phi^{\prime } - 4f^{\prime } \phi + S_{r} \theta^{\prime \prime } - 2K_{l} \phi = 0$$
(14)

The boundary conditions (5) reduce to

$$\begin{aligned} f\left( 0 \right) = S,\quad f^{\prime } \left( 0 \right) = 1,\quad \theta \left( 0 \right) = 1,\quad \phi \left( 0 \right) = 1 \hfill \\ f^{\prime } \left( \eta \right) \to 0,\,\theta \left( \eta \right) \to 0,\quad \phi \left( \eta \right) \to 0\quad {\text{as}}\,\,n \to \infty \hfill \\ \end{aligned}$$
(15)

where Gr x is the Grashof number, \(\tau\) is the mixed convection parameter, Re is the Reynolds number, \(N_{1}\) the buoyancy ratio, M is the magnetic field parameter, \(\xi\) is the aligned angle, K porous medium parameter, Pr is the Prandtl number, R is the radiation parameter, Q is the heat generation/absorption parameter, Ec is the viscous dissipation parameter, D f is the Dufour number, S r is the Soret number, Sc is the Schmidt number and K l is the chemical reaction parameter. These are given by

$$\begin{aligned} Gr_{x} = \frac{{g(\rho \beta )_{nf} T_{0} l^{3} e^{2x/l} }}{{\rho_{nf} \upsilon_{nf}^{2} }},\quad Re = \frac{{u_{w} l}}{{\upsilon_{f} }},\quad N_{1} = \frac{{\left( {\rho \beta^{\prime } } \right)_{nf} C_{0} }}{{\left( {\rho \beta } \right)_{nf} T_{0} }},\quad M = \frac{{2\sigma B_{0}^{2} l}}{{\rho_{nf} u_{0} }},\quad K = \frac{{2\upsilon_{nf} }}{{u_{w} k'}},\quad Pr = \frac{{\upsilon_{f} }}{{\alpha_{f} }}, \hfill \\ R = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{kk^{*} }},\alpha_{f} = \frac{{k_{f} }}{{\left( {\rho c_{p} } \right)_{f} }},Q = \frac{{Q_{0} T_{0} }}{{\upsilon_{f} \left( {\rho c_{p} } \right)_{nf} }}\quad Ec = \frac{{u_{0}^{2} }}{{\left( {c_{p} } \right)_{f} T_{0} }},D_{f} = \frac{{D_{m} K_{T} C_{0} }}{{c_{s} c_{p} \upsilon_{f} T_{0} }},S_{r} = \frac{{D_{m} K_{T} T_{0} }}{{T_{m} \upsilon_{f} C_{0} }}, \hfill \\ Sc = \frac{{\upsilon_{f} }}{{D_{m} }},\quad K_{l} = \frac{{\alpha_{f} l}}{{u_{0} }},\tau = \frac{{Gr_{x} }}{{Re^{2} }} \hfill \\ \end{aligned}$$
(16)

The mixed convection parameter \(\tau\) in Eq. (12) represents aiding buoyancy if \(\tau > 0\) and opposing buoyancy if \(\tau < 0\). The coefficient of skin friction \(C_{fx}\), Nusselt and Sherwood numbers \(Nu_{x} ,\,Sh_{x}\) are given by

$$\begin{aligned} C_{fx} &= \frac{{2\mu_{f} }}{{\rho_{f} u_{w}^{2} }}\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} = \sqrt {\frac{2x}{{lRe_{x} }}} f''(0) \hfill \\ Nu_{x} &= - \frac{x}{{\left( {T_{w} - T_{\infty } } \right)}}\,\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} = - \sqrt {\frac{{xRe_{x} }}{2l}} \theta '(0) \hfill \\ Sh_{x} &= - \frac{x}{{\left( {C_{w} - C_{\infty } } \right)}}\left( {\frac{\partial C}{\partial y}} \right)_{y = 0} = - \sqrt {\frac{{xRe_{x} }}{2l}} \phi '(0) \hfill \\ \end{aligned}$$
(17)

where \(Re_{x} = u_{w} x/\upsilon_{f}\) is the local Reynolds number.

Results and discussion

Equations (12)–(14) with the boundary conditions (15) have been solved numerically using bvp4c solver Matlab Package. Equations (12)–(14) are transformed into system of first-order differential equations. We have checked the accuracy of the assumed missing initial condition, by comparing the calculated value of the different variables at the terminal point with the given value by the existence of the difference in improved values so that the missing initial conditions must be obtained. The calculations are carried out by the program using Matlab. The results presented here were obtained for \(\xi = \pi /3\) that represents aligned angle, M = 2 for magnetic field, Pr = 0.71 which corresponds to air and the Schmidt number Sc = 0.22 for hydrogen. The results obtained show the influences of the non-dimensional parameters, namely aligned magnetic field, thermal radiation, heat generation/absorption, cross-diffusion, viscous dissipation, chemical reaction and porous medium on velocity, temperature, concentration, skin friction, local Nusselt and Sherwood numbers.

Figures 1, 2, and 3 show the effect of aligned angle on velocity, temperature and concentration profiles, respectively. It is evident that an increase in the aligned angle decreases the velocity profiles and increases the temperature and concentration profiles of the flow. It may happen due to the reason that an increase in the aligned angle strengthens the applied magnetic field. Generally, an increase in the magnetic field generates the opposite force to the flow, called Lorentz force. This force has tendency to reduce the velocity profiles. Figures 4, 5, and 6 illustrate the effect of radiation parameter on velocity, temperature and concentration profiles, respectively. It is observed from these figures that with the increase in the radiation parameter we noticed a raise in the velocity and temperature profiles of the flow but reduces the concentration profiles of the flow. Increase in radiation parameter releases heat energy to the flow; this energy helps to increase the temperature as well as velocity profiles of the flow. Figures 7, 8, and 9 depict the effect of heat source parameter on velocity, temperature and concentration profiles, respectively. We observed the similar type of effects as we have seen for radiation parameter. It obeys the physical fact that the increase in the heat source parameter reduces the thermal boundary layer thickness and improves the heat transfer rate.

Fig. 1
figure 1

Velocity profiles for different values of \(\xi\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 2
figure 2

Temperature profiles for different values of \(\xi\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 3
figure 3

Concentration profiles for different values of \(\xi\). \(Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 4
figure 4

Velocity profiles for different values of \(R\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = 0.5\)

Full size image
Fig. 5
figure 5

Temperature profiles for different values of \(R\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = 0.5\)

Full size image
Fig. 6
figure 6

Concentration profiles for different values of \(R\). \(Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = 0.5\)

Full size image
Fig. 7
figure 7

Velocity profiles for different values of \(Q\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 8
figure 8

Temperature profiles for different values of \(Q\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 9
figure 9

Concentration profiles for different values of \(Q\). \(\,Ec = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image

Figures 10, 11, and 12 represent the effect of Dufour number on velocity, temperature and concentration profiles of the flow. It is noticed that an increase in the Dufour number enhances the velocity, temperature profiles of the flow and the trend was reversed on the concentration profiles. From these we conclude that an increase in Dufour number enhances the velocity and thermal boundary layer thicknesses. Figures 13, 14, and 15 display the effect of Soret number on velocity, temperature and concentration profiles, respectively. It is evident from the figures that an increase in the Soret number enhances the velocity and concentration profiles and decreases the temperature profiles of the flow. It is due to the fact that the increase in temperature difference and decrease in the concentration differences causes a change in Soret parameter. Figures 16 and 17 depict the effect of viscous dissipation parameter on velocity and temperature profiles, respectively. It is observed that an increase in the dissipation parameter increases the velocity as well as temperature profiles of the flow. Generally, increase in viscosity enhances the thermal conductivity and this will lead to boost the velocity profiles of the flow.

Fig. 10
figure 10

Velocity profiles for different values of \(D_{f}\). \(\,Ec = 0.5,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 11
figure 11

Temperature profiles for different values of \(D_{f}\). \(\,Ec = 0.5,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 12
figure 12

Concentration profiles for different values of \(D_{f}\).\(\,Ec = 0.5,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,Q = R = 0.5\)

Full size image
Fig. 13
figure 13

Velocity profiles for different values of \(S_{r}\). \(\,Ec = 0.5,D_{f} = 0.3,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 14
figure 14

Temperature profiles for different values of \(S_{r}\). \(\,Ec = 0.5,D_{f} = 0.3,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 15
figure 15

Concentration profiles for different values of \(S_{r}\). \(\,Ec = 0.5,D_{f} = 0.3,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 16
figure 16

Velocity profiles for different values of \(Ec\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 17
figure 17

Temperature profiles for different values of \(Ec\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,N_{1} = 1,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image

The effect of buoyancy ratio on velocity, temperature and concentration profiles are, respectively, shown in Figs. 18, 19, and 20. It is clear that an increase in buoyancy ratio develops the fluid velocity and depreciates the temperature and concentration profiles of the flow. The reason for this is buoyancy force acts along the fluid flow and it causes to generate the flow more effectively. But it reduces the thermal and concentration boundary layers. Figures 21, 22, and 23 illustrate the effect of mixed convection parameter on velocity, temperature and concentration profiles of the flow, respectively. We noticed an interesting result that with the increase in the mixed convection parameter initially we observed a hike in the velocity profiles and depreciation in the temperature and concentration profiles of the flow. At \(\eta = \,2\,\) onwards these profiles have taken reverse action. This is due to the fact that an increase in the mixed convection parameter depreciates the momentum boundary layer thickness and enhances the thermal and concentration boundary layer thicknesses at free stream. This shows the domination of the mixed convection parameter on thermal and concentration boundary layers near the free stream. This domination causes to enhance the heat and mass transfer rate along with the friction factor at free stream. The effect of chemical reaction parameter on velocity and concentration profiles is displayed in Figs. 24 and 25, respectively. It is evident from figures that increase in chemical reaction parameter enhances the velocity and concentration profiles of the flow. This obeys the general physical behavior of chemical reaction parameter that an increase in the chemical reaction causes to improve the concentration boundary layer which indirectly helps to develop the velocity profiles. Figures 26 and 27 represent the effect of porosity parameter on velocity and concentration profiles, respectively. It is clear from these figures that porosity parameter has capability to depreciate the velocity and improves the concentration profiles.

Fig. 18
figure 18

Velocity profiles for different values of \(N_{1}\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,Ec = 0.5,K = 0.2,K_{\text{l}} = 2,R = 0.5\)

Full size image
Fig. 19
figure 19

Temperature profiles for different values of \(N_{1}\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,Ec = 0.5,K = 0.2,K_{l} = 2,R = 0.5\)

Full size image
Fig. 20
figure 20

Concentration profiles for different values of \(N_{1}\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,\tau = 1.5,Ec = 0.5,K = 0.2,K_{l} = 2,R = 0.5\)

Full size image
Fig. 21
figure 21

Velocity profiles for different values of \(\tau\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K = 0.2,K_{l} = 2,R = 0.5\)

Full size image
Fig. 22
figure 22

Temperature profiles for different values of \(\tau\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K = 0.2,K_{l} = 2,R = 0.5\)

Full size image
Fig. 23
figure 23

Concentration profiles for different values of \(\tau\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K = 0.2,K_{l} = 2,R = 0.5\)

Full size image
Fig. 24
figure 24

Velocity profiles for different values of \(K_{l}\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K = 0.2,\tau = 1.5,R = 0.5\)

Full size image
Fig. 25
figure 25

Concentration profiles for different values of \(K_{l}\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K = 0.2,\tau = 1.5,R = 0.5\)

Full size image
Fig. 26
figure 26

Velocity profiles for different values of \(K\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K_{l} = 2,\tau = 1.5,R = 0.5\)

Full size image
Fig. 27
figure 27

Concentration profiles for different values of \(K\). \(\,Q = 0.5,D_{f} = 0.3,S_{r} = 0.2,N_{1} = 1,Ec = 0.5,K_{l} = 2,\tau = 1.5,R = 0.5\)

Full size image

Table 1 displays the effects of non-dimensional parameters on friction factor, Nusselt and Sherwood numbers. From these we noticed that an increase in the aligned angle, magnetic field parameter and porosity parameter reduces the friction factor, rate of heat and mass transfers. But mixed convection parameter shows reverse action to above case. An increase in the heat source parameter, radiation parameter and viscous dissipation parameter increases the skin friction coefficient, mass transfer rate but decreases the heat transfer rate. Soret number and chemical reaction parameter improve the friction factor and Nusselt number but depreciate the Sherwood number. Prandtl and Dufour numbers have capability to enhance the heat transfer rate and reduce the friction factor and rate of mass transfer.

Table 1 The effect of various parameters on skin friction, heat and mass transfer coefficients
Full size table

Concluding remarks

The present model has exploited a number of simplifications to focus on the principal effects of aligned magnetic field, thermal radiation, heat generation/absorption, cross-diffusion, viscous dissipation, heat source and chemical reaction of a nanofluid past an exponentially stretching sheet in porous medium. Our observations have been based on effects of pertinent parameters on velocity, temperature and concentration profiles. We have also summarized observations based on skin friction, local Nusselt and Sherwood numbers through graphs and tables.

The findings of the numerical results are summarized as follows:

  • An increase in the aligned angle strengthens the magnetic field parameter and depreciates the velocity profiles.

  • A rise in the values of radiation parameter, heat source parameter and Eckert number reduces the heat transfer rate and improves the mass transfer rate.

  • Porosity parameter, Prandtl and Soret numbers have tendency to reduce the skin friction coefficient.

  • Chemical reaction parameter does not show significant difference in friction coefficient but it reduces the heat transfer rate as well as the concentration profiles.

  • Mixed convection parameter shows variations in velocity, temperature and concentration profiles and helps to enhance the heat and mass transfer rate along with friction factor.

  • Buoyancy parameter helps to enhance the velocity profiles of the flow and depreciates the temperature and concentration profiles.