Introduction

The wavelike muscular contractions in tubular structures, particularly organs of the digestive scheme such as the throat and the bowels, peristalsis is characterized by exchange reduction and recreation, which pushes ingested food through the digestive tract towards its discharge at the anus. Worms boost themselves through peristaltic faction. After the initial search of Latham (1966), a numeral of systematic, algebraic and trial studies of peristaltic flows of different fluids have been reported under different situations with allusion to physiological and perfunctory situations see Refs. Shapiro et al. (1969), Akbar and Butt (2015a, b), Akbar (2015a, b).

The attention in nanofluids as latent heat transfer fluids spiked originally owing to extremely promise consequences on the improved thermal conductivity for a nanofluid containing copper in impel oil but was disclaimed (Eastman et al. 1997) afterward when manifold investigators' groups experienced a assortment of obtainable combinations of fluids and nanoparticles. Efficient thermal conductivity of mixtures of fluids and nanometer-size particles is deliberate by a steady-state parallel-plate method discussed by Wang et al. (1999). A new thermal conductivity model for nanofluids is discussed by Koo and Kleinstreuer (2004). According to them micro-scale interaction may occur between hot and cold regions, resulting in a lower local temperature gradient for a given heat flux compared with the pure liquid case. Koo and Kleinstreuer (2004) report an experimental correlation for the thermal conductivity of Al2O3 nanofluids as a function of nanoparticle. They pragmatic that the Brownian motion of nanoparticles constitutes a input instrument of the thermal conductivity enhancement with increasing temperature and decreasing nanoparticle sizes. Chon et al. (2005), Nield and Kuznetsov (2009) analyzed Cheng–Minkowycz problem for natural convective boundary-layer flow and double-diffusive natural convective boundary-layer flows. Very recently Sheikholeslami et al. (2011) studied the stream of nanofluid and heat transfer uniqueness between two horizontal plates in a revolving system. The subordinate plate is a stretching sheet and the upper one is a solid porous plate. Copper Cu as nanoparticle and water as its base fluid have been considered. They found that for both suction and injection, the heat transfer rate at the surface increases with increasing the nanoparticle volume fraction, Reynolds number and injection/suction parameter and it decreases with power. More applications of nanoparticles can be seen through Refs. Sheikholeslami et al. (2012), Kuznetsov and Nield (2010), Vajravelu et al. (2011), Hamad and Ferdows (2012a, b), Akbar and Nadeem (2011, 2012, Akbar 2013), Ellahi et al. (2013), Ellahi et al. (2013), Nadeem et al. (2014), Ellahi et al. (2014), Nadeem et al. (2014).

The present article discussed an incompressible viscous fluid containing copper nanoparticles in an asymmetric channel. Thermal and velocity slip effects are also taken into account. The copper nanoparticles for the peristaltic flow water as base fluid is not explored so far. The equations for the purposed fluid model are developed first time in literature and simplified using long wavelength and low Reynolds number assumptions. Exact solutions have been calculated for velocity, pressure gradient, the solid volume fraction of the nanoparticles and temperature profile. The influence of various flow parameters on the flow and heat transfer characteristics is obtained.

Formulation of the problem

Let us considere an incompressible MHD coppernano fluid with water as base fluid in an asymmetric channel with thermal and velocity slip; sinusoidal wave propagating down the walls of the channel. Asymmetric in the channel flow is due to the subsequent hedge surfaces terminology:

$$\begin{aligned} Y&= \bar{H}_{1}=d_{1}+a_{1}\cos \left[ \frac{2\pi }{\lambda }\left( \bar{X} -c_{1}\bar{t}\right) \right], \nonumber \\ Y& = \bar{H}_{2}=-d_{2}-b_{1}\cos \left[ \frac{2\pi }{\lambda }\left( \bar{X} -c_{1}\bar{t}\right) +\omega \right]. \end{aligned}$$
(1)

In the above equations \(a_{1}\) and \(b_{1}\) denote the waves amplitudes, \( \lambda \) is the wave length, \(d_{1}+d_{2}\) is the channel width, \(c_{1}\) is the wave speed, \(\bar{t}\) is the time, \(\bar{X}\) is the direction of wave propagation and \(\bar{Y}\) is perpendicular to \(\bar{X}.\) The expressions for fixed and wave frames are related by the following relations

$$\begin{aligned} \bar{x}=\bar{X}-c_{1}t,\ y=\bar{Y},\ \bar{u}=\bar{U}-c_{1},\ \bar{v}=\bar{V} ,\ p\left( \bar{x}\right) =P\left( \bar{X},t\right) . \end{aligned}$$
(2)

With the transformation given Eq. \((2)\) equations governing the flow and temperature in the presence of heat source or heat sink with viscous dissipation are Hamad and Ferdows (2012a, b)

$$\begin{aligned} \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{\partial \bar{v}}{\partial \bar{y}}=0, \end{aligned}$$
(3)
$$\begin{aligned} \bar{u}\frac{\partial \bar{u}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{u }}{\partial \bar{y}}=-\frac{1}{\rho _{nf}}\frac{\partial P}{\partial \bar{x}} +\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{u}}{\partial \bar{y}^{2} }+\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{u}}{\partial \bar{x} ^{2}}-\frac{\sigma B_{o}^{2}}{\rho _{nf}}\left( \bar{u}c_{1}+c_{1}\right) , \end{aligned}$$
(4)
$$\begin{aligned} \bar{u}\frac{\partial \bar{v}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{v }}{\partial \bar{y}}=-\frac{1}{\rho _{nf}}\frac{\partial P}{\partial \bar{y}} +\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{v}}{\partial \bar{y}^{2} }+\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{v}}{\partial \bar{x} ^{2}}, \end{aligned}$$
(5)
$$\begin{aligned} \bar{u}\frac{\partial \bar{T}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{T }}{\partial \bar{y}}=\alpha _{nf}\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{y}^{2}}+\frac{\partial ^{2}\bar{T}}{\partial \bar{x}^{2}}\right) +\frac{ \mu _{nf}}{\left( \rho c_{p}\right) _{nf}}\left( \frac{\partial \bar{u}}{ \partial \bar{y}}+\frac{\partial \bar{v}}{\partial \bar{x}}\right) ^{2}, \end{aligned}$$
(6)

where \(\bar{x}\) and \(\bar{y}\) are the coordinates along and perpendicular to the channel, \(\bar{u}\) and \(\bar{v}\) are the velocity components in the \( \bar{x}\)- and \(\bar{y}\)-directions, respectively, \(\bar{T}\) is the local temperature of the fluid. Further, \(\rho _{\rm nf}\) is the effective density, \( \mu _{\rm nf}\) is the effective dynamic viscosity, \((\rho c_{p})_{\rm nf}\) is the heat capacitance, \(\alpha _{\rm nf}\) is the effective thermal diffusivity, and \( k_{\rm nf} \) is the effective thermal conductivity of the nanofluid, which are defined as [see Refs. Hamad and Ferdows (2012a, b)]

$$\begin{aligned} \rho _{nf}&= \left( 1-\phi \right) \rho _{f}+\phi \rho _{f},\,\mu _{nf}=\frac{\mu _{f}}{\left( 1-\phi \right) ^{2.5}}, \\ \left( \rho c_{p}\right) _{nf}&= \left( 1-\phi \right) \left( \rho c_{p}\right) _{f}+\phi \left( \rho c_{p}\right) _{s},\,\alpha _{nf}= \frac{k_{nf}}{\left( \rho c_{p}\right) _{nf}}, \\ k_{nf}&= k_{f}\left( \frac{k_{s}+2k_{f}-2\phi \left( k_{f}-k_{s}\right) }{ k_{s}+2k_{f}+2\phi \left( k_{f}-k_{s}\right) }\right) \end{aligned}$$
(7)

where \(\phi \) is the solid volume fraction of the nanoparticles.

we introduce the following non-dimensional quantities

$$\begin{aligned} x&= \frac{2\pi \bar{x}}{\lambda },\,y=\frac{\bar{y}}{d_{1}},\,u= \frac{\bar{u}}{c_{1}},\,v=\frac{\bar{v}}{c_{1}},\,t=\frac{2\pi \bar{t}}{\lambda },\,\delta =\frac{2\pi d_{1}}{\lambda },\,d= \frac{d_{2}}{d_{1}},\,P=\frac{2\pi d_{1}^{2}P}{\mu c_{1}\lambda }, \\ h_{1}&= \frac{\bar{h}_{1}}{d_{1}},\,h_{2}=\frac{\bar{h}_{2}}{d_{2}}, \,\mathrm{Re}=\frac{\rho c_{1}d_{1}}{\mu },\,a=\frac{a_{1}}{d_{1}}, \,b=\frac{a_{2}}{d_{1}},\,d=\frac{d_{2}}{d_{1}},\,S=\frac{ \bar{S}d_{1}}{\mu c_{1}}, \\ \theta&= \frac{\bar{T}-\bar{T}_{0}}{\bar{T}_{1}-\bar{T}_{0}},\,P_{r}= \frac{\nu }{\alpha },\,E_{c}=\frac{c_{1}^{2}}{\left( \bar{T}_{1}-\bar{T }_{0}\right) \bar{T}_{0}\left( c_{p}\right) _{f}}. \end{aligned}$$
(8)

in above equations \(P_{r}\) is the Prandtl number and \(E_{c}\) is the Eckert number.

Stream function and velocity field are related by the expressions

$$\begin{aligned} u=\frac{\partial \Psi }{\partial y},\quad v=-\delta \frac{\partial \Psi }{ \partial x}, \end{aligned}$$
(9)

In view of the Eqs. 7–9 under the long wavelength and low Reynolds number assumption we have the following equations

$$\begin{aligned} \frac{\partial ^{4}\Psi }{\partial y^{4}}-M^{2}\left( 1-\phi \right) ^{2.5} \frac{\partial ^{2}\Psi }{\partial y^{2}}=0, \end{aligned}$$
(10)
$$\begin{aligned} \frac{{\rm {d}}P}{{\rm {d}}x}=\frac{\partial }{\partial y}\left[ \frac{\partial ^{2}\Psi }{ \partial y^{2}}-M^{2}\left( 1-\phi \right) ^{2.5}\left( \frac{\partial \Psi }{\partial y}+1\right) \right], \end{aligned}$$
(11)
$$\begin{aligned} \frac{\partial ^{2}\theta }{\partial y^{2}}+{\left (\frac {k_{f}} {k_{nf}} \right)} \frac{E_{c}\Pr }{\left( 1-\phi \right) ^{2.5}}\left( \frac{\partial ^{2}\Psi }{\partial y^{2}}\right) ^{2}=0, \end{aligned}$$
(12)

The non-dimensionless boundary conditions

$$\begin{aligned} \Psi= & {} \frac{F}{2},\,\frac{\partial \Psi }{\partial y}=-\beta \frac{ \partial ^{2}\Psi }{\partial y^{2}}-1,\quad {\text{at}} \quad y=h_{1}=1+a\cos x, \end{aligned}$$
(12a)
$$\begin{aligned} \Psi= -\frac{F}{2},\,\frac{\partial \Psi }{\partial y}=\beta \frac{ \partial ^{2}\Psi }{\partial y^{2}}-1,\quad {\text{at}}\quad y=h_{2}=-d-b\cos \left( x+\phi \right), \end{aligned}$$
(12b)
$$\begin{aligned} \theta +\gamma \frac{\partial \theta }{\partial y}= 0,\quad {\text{at}}\quad y=h_{1},\,\theta -\gamma \frac{\partial \theta }{\partial y}=1,\quad {\text{at}}\quad y=h_{2}, \end{aligned}$$
(12c)

The flow rates in fixed and wave frame are related by

$$\begin{aligned} Q=F+1+d. \end{aligned}$$
(13)

Solution profiles

Exact solutions for stream function, temperature profile and pressure gradient can be written as

$$\begin{aligned} \Psi \left( x,y\right)&= \left( \cosh \left( y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) -\sinh \left( y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5} }\right) \right) \left( L_{2}\right. \\&\quad+L_{1}\cosh \left( 2y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) +L_{1}\sinh \left( 2y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad+L_{3}y. \end{aligned}$$
(14)
$$\begin{aligned} \frac{{\text{d}}P}{{\text{d}}x}=-1-\frac{F\beta }{2}-\frac{F\coth \left( \frac{1}{2} (h_{1}-h_{2})\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) }{2\sqrt{ M^{2}\left( 1-\phi \right) ^{2.5}}}, \end{aligned}$$
(15)
$$\begin{aligned} \theta \left( x,y\right)&= (E_{c}\Pr {\left (\frac {k_{f}} {k_{nf}} \right)} (-\left( L_{4}^{2}+L_{5}^{2}\right) \cosh \left( 2y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) -2(\left( L_{4}^{2}-L_{5}^{2}\right) M^{2}y^{2} \nonumber \\&\quad\left( 1-\phi \right) ^{2.5}+L_{4}L_{5}\sinh \left( 2y\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) )/8M^{2}\left( 1-\phi \right) ^{5}+L_{10}y+L_{11}, \end{aligned}$$
(16)

\(L_{1}-L_{9}\) are constants evaluated using Mathematica 8.

$$\begin{aligned} L_{1}&= \frac{1}{4}F\csc h\left( (h_{1}-h_{2})\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \left( \cosh \left( h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \right. \\&\quad+\cosh \left( h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) -\sinh \left( h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad-\sinh \left( h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) , \\ L_{2}&= -\frac{1}{4}F\csc h\left( (h_{1}-h_{2})\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \left( \cosh \left( h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \right. \\&\quad+\cosh \left( h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) +\sinh \left( h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad+\sinh \left( h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) , \\ L_{3}&= -1-\frac{F\beta }{2}-\frac{F\coth \left( \frac{1}{2}(h_{1}-h_{2}) \sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) }{2\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}}, \\ L_{4}&= (L_{1}+L_{2}),\,L_{5}=(L_{1}-L_{2}),\,L_{6}=E_{c}\Pr (-\left( L_{4}^{2}+L_{5}^{2}\right) \cosh \left( 2h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad\left. -2\left( h_{1}^{2}\left( L_{4}^{2}-L_{5}^{2}\right) M^{2}\left( 1-\phi \right) ^{2.5}+L_{4}L_{5}\sinh \left( 2h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \right. \right) /8M^{2}\left( 1-\phi \right) ^{5}, \\ L_{7}&= E_{c}\Pr (-\left( L_{4}^{2}+L_{5}^{2}\right) \cosh \left( 2h_{2} \sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) -2\left( h_{1}^{2}\left( L_{4}^{2}-L_{5}^{2}\right) M^{2}\left( 1-\phi \right) ^{2.5}+\right. \\&\quad\left. L_{4}L_{5}\sinh \left( 2h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5} }\right) \right) /8M^{2}\left( 1-\phi \right) ^{5}, \\ L_{8}&= E_{c}\Pr (-2(2h_{1}\left( L_{4}^{2}-L_{5}^{2}\right) M^{2}\left( 1-\phi \right) ^{2.5}+2L_{4}L_{5}M\left( 1-\phi \right) ^{\frac{5}{4}}\cosh \left( 2h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad+2\left( -L_{4}^{2}-L_{5}^{2}\right) \sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\sinh \left( 2h_{1}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) )/8M^{2}\left( 1-\phi \right) ^{5}, \\ L_{9}&= E_{c}\Pr (-2(2h_{2}\left( L_{4}^{2}-L_{5}^{2}\right) M^{2}\left( 1-\phi \right) ^{2.5}+2L_{4}L_{5}M\left( 1-\phi \right) ^{\frac{5}{4}}\cosh \left( 2h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) \\&\quad+2\left( -L_{4}^{2}-L_{5}^{2}\right) \sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\sinh \left( 2h_{2}\sqrt{M^{2}\left( 1-\phi \right) ^{2.5}}\right) )/8M^{2}\left( 1-\phi \right) ^{5}, \\ L_{10}&= -\frac{\left( h_{1}+\gamma \right) \left( 1+L_{6}-L_{7}+L_{8}\gamma +L_{9}\gamma \right) }{h_{1}-h_{2}+2\gamma },\,L_{11}=-\frac{\left( 1+L_{6}-L_{7}+L_{8}\gamma +L_{9}\gamma \right) }{ h_{1}-h_{2}+2\gamma }. \end{aligned}$$

The dimensionless pressure rise \(\Delta P\) is

$$\begin{aligned} \Delta P=\mathop {\displaystyle \int }\limits _{0}^{1}\left( \frac{{\rm d}P}{{\rm d}x}\right) {\rm d}x. \end{aligned}$$
(17)

Graphical illustration

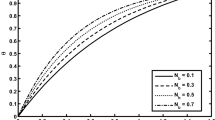
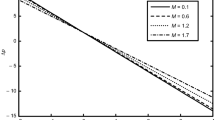
Here we discussed the characteristics of the flow, the heat transfer, pressure rise, pressure gradient, velocity, temperature profile, nanoparticle fraction and streamlines. For the flow parameters numerical values are plotted in Figs. 1, 2, 3, 4, 5. Analysis has been done for Cu nanoparticles with water as a base fluid in connection with velocity and thermal slips. Numerical integration is carried out for the pressure rise per wavelength. The pressure rise against volume flow rate for the solid volume fraction of the nanoparticles \(\phi,\) Hartmann number \(M\), velocity slip parameter \( \beta \) and amplitude \(a\) is portrayed in the Fig. 1a–d. It is noticed that the pressure rise and volume flow rate have opposite behaviors. From Fig.1a–d it is found that in pumping region (\(\Delta P>0\)), the pressure rise decreases with the increase of Hartmann number \(M\) while pressure rise increase with the increase in the solid volume fraction of the nanoparticles \(\phi,\) velocity slip parameter \(\beta \) and amplitude \(a.\) Fig.1a–d also show that in the augmented pumping region for (\(\Delta P<0\)), pressure rise gives the opposite results for all the parameter as compared to the pumping region (\(\Delta P>0\)). Free pumping region exists when \(\left( \Delta P=0\right) \). It is also seen that pressure rise for Cu–water is greater than for pure water \((\phi =0)\). Variations of Hartmann number \(M,\) velocity slip parameter \(\beta \) and solid volume fraction of the nanoparticles \(\phi \) on the velocity profile are shown in the Fig.2a–c. It is depicts that the behavior of velocity is not similar in view of the Hartmann number \(M\) and solid volume fraction of the nanoparticles \(\phi \). The velocity field increases due to increase in \(\phi \) while velocity field decreases with an increase in \(M.\) It is also observed that velocity field for Cu–water is greater than for pure water \((\phi =0).\) It is also noticed that velocity field increases with increase in velocity slip parameter \( \beta .\)

The pressure gradient for different values of \(M,\,a\) and \(\phi \) are plotted in the Fig. 3a–d. Magnitude of pressure gradient increases with the increase in \(M\) and \(\phi \). It is also observed that the maximum pressure gradient occurs when \(x=0.48\ \)and near the channel walls the pressure gradient is small. This leads to the fact that flow can easily pass in the middle of the channel. It is analyzed that near the channel walls pressure gradient increases with an increase in \( a,\) while at centre pressure gradient decreases for large values of \(a.\) It is also observed that pressure gradient for Cu–water is greater than for pure water \((\phi =0).\)

Variations of temperature profile for different values of Prandtl number \( P_{r}\), Eckert number \(E_{c}\) thermal slip parameter \(\gamma \) and solid volume fraction of the nanoparticles \(\phi \) are seen through Fig. 4a–d that when we increase Prandtl number \(P_{r}\), Eckert number \(E_{c},\) thermal slip parameter \(\gamma \) and solid volume fraction of the nanoparticles \(\phi \) the temperature profile increases. It is also seen that temperature for Cu–water is greater than for pure water \((\phi =0)\) with the varying values of Eckert number \(E_{c}\) and thermal slip parameter \(\gamma \) but for varying values of Prandtl number \( P_{r}\) temperature for Cu–water is smaller than for pure water \((\phi =0).\)

The trapping for different values of \(M,\) \(\beta \) and \(\phi \) are shown in the Fig. 5a–d. It is seen from Fig. 5a, b that with the increase in the value of the \(M\) size of the trapping bolus decreases in upper part of the channel but increases in the lower part of the channel. Streamlines for different values of \(\phi \) have been plotted in the Fig. 5c, d. It is found that when we go from pure water to Cu–water, the size of the trapping bolus increases while number of bolus decreases. With the increase in slip parameter \(\beta \) size of the trapping bolus decreases in upper part of the channel but increases in the lower part of the channel. Number of bolus increases in upper part of the channel but decreases in the lower part of the channel with increase in \(\beta.\)

Fig. 1
figure 1

Pressure rise versus flow rate for \(d=1,\,b=0.7\) and \(\omega =0.7\)

Full size image
Fig. 2
figure 2

Velocity profile for \(a=0.3,\,d=1,\,\phi =0.7,\,b=0.5,\,x=1,\, Q=-2\)

Full size image
Fig. 3
figure 3

Pressure gradient for \(d=1,\,\phi =0.7,\,b=0.5,\,Q=-2\)

Full size image
Fig. 4
figure 4

Temperature profile for a Pr = 0.3, b Ec = 0.1, c Pr = 6.8 and \(E_{c}=0.1\) other parameters \(a=0.3,\,d=1,\,\phi =0.7,\,b=0.5,\,x=1,\,Q=-2\)

Full size image
Fig. 5
figure 5

Streamlines for a, b where \(M=2,\,4, \) c, d for \(\phi =0.0,\,0.1,\) e, f \(\beta =0.2,\,0.4\) other parameters are \(d=1,\,\phi =0.7,\,b=0.5,\,Q=-2\)

Full size image
Table 1 Thermal properties of base fluid (water) and nanoparticles
Full size table