Introduction

Waterflooding is a commonly used method to enhance the recovery in oil field development (Stenger et al. 2009; Wen et al. 2014). The ratio of injection–production control area acts as an important role in waterflooding reservoir, which is applied to evaluate the development effect (Siavashi et al. 2016) and calculate oilfield development index (Song et al. 2000; Feng et al. 2013). The ratio of injection–production control area is influenced by permeability, oil saturation, injection–production pressure drop and injector–producer spacing (Jiang 2013). There are three typical approaches to determine the ratio of injection–production control area: (1) streamline numerical simulation, (2) empirical method and (3) dynamical split method.

In order to apply streamline numerical simulation to determine the ratio of injection–production control area, geology model, fluid property and well schedule are needed to build the streamline model. The FrontSim Numerical Simulator, a separate simulator in ECLIPSE (GeoQuest 2010), is usually applied to calculate the distribution of streamline. Based on the distribution of streamline, the ratio of injection–production control area can be determined. Siavashi et al. (2016) used streamline-based simulation to obtain the injection–production control area, which is also called sweep region, to reflect the development performance of waterflooding reservoir. However, this method calls for a long time to build and calculate the streamline model, making itself time-consuming work (Stenerud et al. 2008; Bhambri and Mohanty 2011). Besides, considering the available parameters and expense, not all waterflooding reservoirs have the ability to conduct the streamline numerical simulation. For the empirical method, the angular bisector of two neighboring injector–producer lines is used to divide the injection–production control area (Ji et al. 2008; Feng et al. 2013). This method is fit for the homogeneous reservoir and it is easy to be applied. Ji et al. (2008) divided the injection–production control area by the angular bisector of two neighboring injector–producer lines to calculate oil production for 4-spot, 5-spot and invert 9-spot areal well patterns. However, this method neglects the influence from geological parameters and well schedule. Therefore, this method is not fit for the heterogeneous reservoir. In order to deal with the ratio of injection–production control area in heterogeneous reservoir, Feng et al. (2013) developed a dynamical split method. This method calculates the ratio of injection–production control area according to percolation resistance and displacement pressure. However, it needs a lot of iterations in the process of development index calculation which is also a time-consuming work.

Having addressed these problems, there is an important need to establish a comprehensive and reliable prediction formula for the ratio of injection–production control area that can simultaneously consider the heterogeneous parameters and well schedule and quickly determine the ratio. One approach to get the relationship between the ratio of injection–production control area and multiple factors is artificial neural networks (ANNs). ANN is a powerful tool to model the complex relationship between inputs and outputs (Ketineni et al. 2015; Kurt and Kayfeci 2009). There are input hidden and output layers included in the widely used ANN models (Enab and Ertekin, 2014; Togun and Baysec 2010; Valeh-e-Sheyda et al. 2010). By training the data, the relationship between inputs and outputs can be obtained (Jung and Kwon 2013; Sayyad et al. 2014). However, this method cannot provide explicit function forms. In order to get the explicit function between independent and dependent variables, multivariate parametric regressions are usually applied (Yuan et al. 2007). Origin is a commonly used software for analyzing data and fitting curve, which is one of the most powerful and most widely used analysis tools (Bimbo et al. 2016; Böllmann et al. 2016). In this paper, we apply Origin software to obtain the prediction formula for ratio of injection–production control area.

This paper develops a prediction formula for ratio of injection–production control area. Firstly, 410 sets of streamline models, which have the different permeability, oil saturation, injection–production pressure drop and injector–producer spacing, are built to acquire the database of ratio of injection–production control area. Then based on the database, the prediction formula is built by multivariate parametric regression. The error analysis of this prediction formula is conducted by normality and homoscedasticity tests and standardized residual diagnostics to confirm the statistical significance. Finally, in order to approve the accuracy of the established formula, this formula is applied to calculate the ratio of injection–production control area for a new synthetic reservoir model.

Methodology

In order to get the prediction formula, the database is acquired from a series of simulation models firstly. Then based on the database, multivariate parametric regression is applied to obtain the explicit function form. To validate the accuracy of this established prediction formula, error analysis is conducted by normality and homoscedasticity tests, standardized residual and prediction formula application.

Database acquirement

In this study, we apply the FrontSim Numerical Simulator to calculate the streamline distribution for a series of reservoir models. Then the injection–production control area can be measured and a database can be acquired.

There are totally 410 simulation schemes which are utilized to establish the prediction formula for ratio of injection–production control area. The basic parameters for these models are same. The reservoir model is a single-layer model. The depth of the top face is 2000 m. The initial reservoir pressure is 20 MPa. The porosity is 0.25. The density of oil is 890 kg/m3, and the density of formation water is 1000 kg/m3.

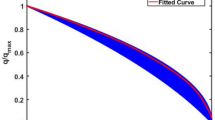
The basic assumptions include: (1) the model contains oil and water two-phase flow; (2) the fluid flow obeys Darcy’s law; (3) the displacement process is isothermal; (4) the fluid flow without considering gravity and capillary pressure. The oil and water relative permeability curve is plotted in Fig. 1. There is one injector and two producers. All producers and injectors are controlled by bottom hole pressure (BHP). There is no flow through the reservoir boundary. The total production time is 1800 days. All models have the same area.

Fig. 1
figure 1

Oil and water relative permeability curve

Full size image

According to the relative positions of injectors and producers, each reservoir model is separated into two regions (shown in Fig. 2). Because the waterflooding process is mainly affected by the parameters on mainstream line (Zhou et al. 2016; Feng et al. 2013), the parameters of each part are assumed to be equal to the average parameters of injector–producer line.

Fig. 2
figure 2

Sketch of reservoir model

Full size image

There are four parameters changed for these 410 simulation schemes. They are (1) permeability k, (2) the present oil saturation S o, (3) injection–production pressure drop Δp calculated by the bottom hole pressure (BHP) of injector minus the BHP of producer and (4) injector–producer spacing L. The ratios of the two regions’ permeability k 1/k 2, oil saturation S o1/S o2, injection–production pressure drop Δp 1/Δp 2 and injector–producer spacing L 1/L 2 can affect the ratio of injection–production control area θ 1/θ 2. These four parameters are changed for each model. The ranges of k 1/k 2, S o1/S o2, Δp 1/Δp 2 and L 1/L 2 are from 0.14 to 7.00, from 0.42 to 2.33, from 0.33 to 2.00 and from 0.58 to 1.72, respectively. The permeability and oil saturation for each region in one model is different while the average permeability and oil saturation of all models is same. The simulation models with different injector–producer spacing and permeability distribution can be seen in Fig. 3. Based on the streamline distribution, θ 1/θ 2 is measured.

Fig. 3
figure 3

Simulation models of different injector–producer spacing and permeability distribution

Full size image

Fitting tool

The ratio of injection–production control area θ 1/θ 2 is influenced by the joint action of multiple factors. Their respective effect may be masked or enforced by another, which increases the difficulty in discovering the underlying relationship between them (Feng et al. 2014). In order to obtain the explicit function form, multivariate parametric regression is applied. Based on the 410 results, it is easily to acquire the regression forms relating dependent and independent variables. The four independent variables are independent of each other.

In order to conduct the multivariate parametric regression, the explicit function form of the ratio of injection–production control area θ 1/θ 2 and one independent variable, which is one of the ratio of the two regions’ permeability k 1/k 2, oil saturation S o1/S o2, injection–production pressure drop Δp 1/Δp 2 and injector–producer spacing L 1/L 2, is obtained through the 410 results, respectively. By combining the four explicit function forms into one comprehensive function, the mathematical correlation between the dependent and four independent variables can be obtained. In this work, the parameters are calculated using the comprehensive function in the nonlinear curve fitting tool available in Origin Pro 8.5 (OriginLab Corporation, Northampton, MA, USA).

Error analysis

Normality and homoscedasticity tests

Normality and homoscedasticity tests are important measures in analyzing the statistical correlation errors. We use T-test to analyze the normality and F-test to assess the homoscedasticity. The null hypothesis is evaluated by T-test where the data are coming from an unspecified normal distribution (Zhang et al. 2015). If the test result is zero, the null hypothesis cannot be rejected at the 5% significance level, in which case the data are normal distribution. The F-test is to evaluate the null hypothesis by comparing the variance of two independent samples. If the variance is equal, the null hypothesis cannot be rejected at the 5% significant level.

Standardized residual

Standardized residual is used to describe the division of a residual by an estimate of its standard deviation, which is a useful method to find the hidden structures in the data (Huisman et al. 1993; Mohammadi et al. 2012). The standardized residual can be formulated as:

$$e_{\text{is}} = \frac{{y_{\text{cal}} - y_{\text{mea}} }}{{\sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {y_{\text{cal}} - y_{\text{mea}} } \right)^{2} } }}{N - 1}} }}$$
(1)

where e is is the standardized residual; y cal is the calculated result by the prediction function; y mea represents the measured result; N is the total number of data used to obtain the prediction function.

Then the standardized residual distribution can be plotted, in which x-coordinate is for the calculated y cal and y-coordinate is for the standardized residual. If there are more than 95% standardized residuals falling in the range [−2, 2] randomly and the standardized residuals have zero mean, it represents the prediction model is correct (Chelgani et al. 2010; Rousseeuw and Leroy 1987).

Prediction formula application

The development of the prediction formula aims at quickly dividing the injection–production control area. In order to validate the feasibility and accuracy of this prediction formula, we apply this prediction formula to predict the ratio of injection–production control area for a synthetic reservoir model. Then the ratio of injection–production control area for a synthetic reservoir model is also calculated by streamline numerical simulator. If the results calculated by the two methods match well, it means that this prediction formula can be used to predict the ratio of injection–production control area without running streamline numerical simulator.

Results and discussion

Based on 410 sets of measured results, the prediction formula for ratio of injection–production control area in triangle well pattern is established. The results of error analysis validate the accuracy of this prediction formula. Then analysis of range is applied to determine the influence degree of each variable on the ratio of injection–production well control area θ 1/θ 2. Finally, the comparison of the injection–production control area for a new synthetic reservoir model calculated by this prediction formula and streamline numerical simulator is conducted.

Prediction formula

There are totally 410 sets of measured results. The typical curves of the ratio of injection–production control area are illustrated in Fig. 4. In order to give a comprehensive prediction formula, the function form of the ratio of injection–production control area θ 1/θ 2 and one independent variable is obtained according to the trend of these curves.

Fig. 4
figure 4

Division of injection–production control area versus the ratio of two regions’ a permeability; b oil saturation; c injection–production pressure drop; d injector–producer spacing

Full size image

For the ratio of the two regions’ injector–producer spacing and oil saturation, the data can be fitted with a quadratic polynomial and linear, respectively:

$$\frac{{\theta_{1} }}{{\theta_{2} }} = a_{1} \left( {\frac{{L_{1} }}{{L_{2} }}} \right)^{2} + a_{2} \left( {\frac{{L_{1} }}{{L_{2} }}} \right) + a_{3}$$
(2)
$$\frac{{\theta_{1} }}{{\theta_{2} }} = b_{1} \left( {\frac{{S_{{{\text{o}}1}} }}{{S_{{{\text{o}}2}} }}} \right) + b_{2}$$
(3)

where θ 1/θ 2 is the ratio of injection–production control area; L 1/L 2 is the ratio of two regions’ injector–producer spacing; S o1/S o2 is the ratio of two regions’ oil saturation; a 1, a 2, a 3, b 1, b 2 are the fitting parameters.

For the ratio of the two regions’ injection–production pressure drop and permeability, the fitting type can be written as:

$$\frac{{\theta_{1} }}{{\theta_{2} }} = c_{1} {\text{e}}^{{c_{2} \ln \left( {\frac{{\Delta p_{1} }}{{\Delta p_{2} }}} \right)}} + c_{3}$$
(4)
$$\frac{{\theta_{1} }}{{\theta_{2} }} = d_{1} \left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right)^{2} +\,d_{2} \left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right) + d_{3}$$
(5)

where Δp 1/Δp 2 is the ratio of two regions’ injection–production pressure drop; k 1/k 2 is the ratio of two regions’ permeability; c 1, c 2 c 3, d 1, d 2, d 3 are the fitting parameters.

Therefore, the mathematical model between the dependent and four independent variabilities can be written as:

$$\frac{{\theta_{1} }}{{\theta_{2} }} = a_{1} \left( {\frac{{L_{1} }}{{L_{2} }}} \right)^{2} +\,a_{2} \left( {\frac{{L_{1} }}{{L_{2} }}} \right) + b_{1} \left( {\frac{{S_{{{\text{o}}1}} }}{{S_{\text{o2}} }}} \right) + c_{1} {\text{e}}^{{c_{2} \ln \left( {\frac{{\Delta p_{1} }}{{\Delta p_{2} }}} \right)}} + d_{1} \left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right)^{2} +\,d_{2} \left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right) + f$$
(6)

where f is the constant.

Equation (6) is the prediction formula for ratio of injection–production control area in triangle well pattern. The ratios of two regions’ permeability k 1/k 2, oil saturation S o1/S o2, injection–production pressure drop Δp 1/Δp 2 and injector–producer spacing L 1/L 2 are the basic parameters of the reservoir. There is no need to run the reservoir simulator to obtain them. By inputting these four parameters of waterflooding reservoir into Eq. (6), the ratio of injection–production control area for this reservoir can be acquired. It is a convenient approach to determine the ratio of injection–production control area, and it can minimize the work volume and time required in running streamline numerical simulator and complex iterations. This model can predict the ratio of injection–production control area θ 1/θ 2 under the same ranges of k 1/k 2, S o1/S o2, Δp 1/Δp 2 and L 1/L 2 with these 410 sets of simulation models and the same assumptions.

These parameters a 1, a 2, b 1, c 1, c 2, d 1, d 2 and f are calculated using Eq. (6) in the nonlinear curve fitting function in OriginLab (Origin Pro 8.5) based on 410 measured results. The fitting curve of these four variables is obtained with a R 2 of 0.96, which shows a very satisfactory performance for the prediction formula (Coulibaly and Baldwin 2005; Ali Ahmadi et al. 2013):

$$\frac{{\theta_{1} }}{{\theta_{2} }} = 0.03194\left( {\frac{{L_{1} }}{{L_{2} }}} \right)^{2} + 0.00322\left( {\frac{{L_{1} }}{{L_{2} }}} \right) - 0.04319\left( {\frac{{S_{{{\text{o}}1}} }}{{S_{{{\text{o}}2}} }}} \right) + 1.89133{\text{e}}^{{0.41604\ln \left( {\frac{{\Delta p_{1} }}{{\Delta p_{2} }}} \right)}} - 0.00013\left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right)^{2} +\,0.20045\left( {\ln \frac{{k_{1} }}{{k_{2} }}} \right) - 0.88330$$
(7)

Normality and homoscedasticity

The measured data and calculated data for θ 1/θ 2 are shown in Fig. 5. It can be seen that the data set are generally fall in a small range around the 45 degree line, indicating a high correlation for the whole database.

Fig. 5
figure 5

Correlation of predicted θ 1/θ 2 versus measured θ 1/θ 2

Full size image

Figure 6 illustrates the difference between measured θ 1/θ 2 and predicted θ 1/θ 2. As illustrated in Fig. 6, the difference follows a normal distribution with a mean of −0.001. T-test and F-test return a decision value of zero. These results indicate that the null hypothesis cannot be rejected at the 5% significance level which confirms the accuracy of the prediction formula.

Fig. 6
figure 6

Difference of predicted θ 1/θ 2 versus measured θ 1/θ 2

Full size image

Residual plots

The distribution of standardized residuals is plotted in Fig. 7. As observed from this figure, there are only 16 out of 410 data points fall out of the domain of −2 ≤ e is ≤+2. This result indicates that more than 95% points fall in [−2, +2] and distribute randomly. It also can approve that the prediction formula satisfies the equal variance.

Fig. 7
figure 7

Calculated standardized residual of predicted θ 1/θ 2 versus measured θ 1/θ 2. Dots represent the outliers

Full size image

Analysis of range

In order to analyze the influence degree of each variable on the ratio of injection–production well control area θ 1/θ 2, analysis of range is applied. There are two steps to conduct analysis of range.

Firstly, the orthogonal experiment is designed to acquire the basic values for analysis of range. The ratio of the two regions’ permeability k 1/k 2, oil saturation S o1/S o2, injection–production pressure drop Δp 1/Δp 2 and injector–producer spacing L 1/L 2 are determined as four factors of the orthogonal experiment. The level for each parameter is three. Therefore, according to the orthogonal design table L 9(34) (Liu et al. 2010), the orthogonal experiment is designed and listed in Table 1.

Table 1 Orthogonal experiment design
Full size table

Secondly, the analysis of range for this designed orthogonal experiment is conducted as shown in Table 2. Each factor in the same level i (i = 1, 2, 3) corresponds to three θ 1/θ 2 values which are listed in Table 1. These three θ 1/θ 2 values of level i are summed by.

$$\left( {\frac{{\theta_{1} }}{{\theta_{2} }}} \right)_{i} = \sum\limits_{j = 1}^{3} {\left( {\frac{{\theta_{1} }}{{\theta_{2} }}} \right)_{i,j} }$$
(8)

where (θ 1/θ 2) i is the sum of three θ 1/θ 2 values of each factor in level i; (θ 1/θ 2) i,j is the jth θ 1/θ 2 value of each factor in level i.

Table 2 Analysis of range table
Full size table

The influence of level i of each factor on the ratio of injection–production control area θ 1/θ 2 is represented by K i and it can be calculated by:

$$K_{i} = \sum\limits_{i = 1}^{3} {\left( {\frac{{\theta_{1} }}{{\theta_{2} }}} \right)_{i} } /3$$
(9)

R is used to denote the range of K i . It reflects the influence degree of each factor on the ratio of injection–production control area θ 1/θ 2. The factor with higher R means a strong effect on θ 1/θ 2 (Cui et al. 2007). R is calculated as:

$$R = K_{\hbox{max} } - K_{\hbox{min} }$$
(10)

From Table 2 we can see that the ratio of two regions’ injector–producer pressure drop has the most influence on the ratio of injection–production control area θ 1/θ 2. The second and the third are the ratio of two regions’ permeability and injector–producer spacing, respectively. The ratio of two regions’ oil saturation has the minimal effect on the ratio of injection–production control area θ 1/θ 2.

Application

The prediction formula Eq. (7) is applied to predict the control area of a new synthetic reservoir model. There are four five-spot well patterns. Nine injectors and four producers are placed in this reservoir. Injectors and producers are all controlled by bottom hole pressure. There are total 16 injector–producer lines, and the whole reservoir model is divided into 32 parts.

Equation (7) is applied to calculate the ratio of injection–production control area. Then based on the total angle between two adjacent injector–producer lines, the control area can be calculated. Streamline numerical simulator is also applied to calculate the control area according to the distribution of streamline. The streamline distribution of this model reflects the actual control area. In order to compare the actual and predicted control areas, the division of control area of this model is shown in Fig. 8. The black lines are calculated by Eq. (7). From Fig. 8 we can see that the predicted and actual results match well. A comparison between predicted and actual control angles is presented in Fig. 9. As shown in Fig. 9, the predicted results by Eq. (7) show a good agreement with the actual control angles. Therefore, the prediction formula established in this paper gives a precise prediction formula for ratio of injection–production control area in triangle well pattern.

Fig. 8
figure 8

Comparison between actual and predicted divisions of control area

Full size image
Fig. 9
figure 9

Comparison between actual and predicted control angle

Full size image

Conclusions

  1. 1.

    A prediction formula for ratio of injection–production control area has been established based on 410 sets of simulation results. The ratio of injection–production control area is influenced by the ratio of the two regions’ permeability, oil saturation, injection–production pressure drop and injector–producer spacing. Based on this prediction formula, the ratio of injection–production control area can be quickly decided.

  2. 2.

    The error analysis of this prediction formula has been conducted. Both normality and homoscedasticity tests and standardized residual diagnostics have confirmed the statistical significance of the results. The application of this prediction formula has also approved the accuracy of this formula.

  3. 3.

    Based on the analysis of range, the ratio of injection–production control area is most affected by the ratio of two regions’ injector–producer pressure. The ratio of two regions’ oil saturation has the minimal effect on the ratio of injection–production control area. The influences of the ratio of two regions’ permeability and injector–producer spacing are moderate.