Introduction

During the last 70 years, engineers developed a significant number of PVT correlations due to the high importance empirical correlations for PVT properties in oil and gas engineering. These correlations are sensitive to the region and number of data points. PVT correlations accuracy varies from one region to another. Therefore, significant numbers of correlations have been developed based on the regional variation, and it is recommended in the previous studies that one should use their own region PVT correlation. A brief overview of the widely used PVT correlation is give below.

Standing (1947, 1977) presented correlations for bubble point pressure and oil formation volume factor. Standing’s correlations were based on laboratory experiments carried out on 105 samples from 22 different crude oils in California. Katz (1942) presented five methods for predicting the reservoir oil shrinkage. Vazquez and Beggs (1980) presented correlations for oil formation volume factor. They divided oil mixtures into two groups, above and below 30 ° API gravity. More than 6000 data points from 600 laboratory measurements were used in developing the correlations. Glaso (1980) developed the correlation for formation volume factor using 45 oil samples from North Sea hydrocarbon mixtures. Al-Marhoun (1988) published correlations for estimating bubble point pressure and oil formation volume factor for the Middle East oils. He used 160 data sets from 69 Middle Eastern reservoirs to develop the correlation. Abdul-Majeed and Salman (1988) published an oil formation volume factor correlation based on 420 data sets. Their model is similar to that of Al-Marhoun (1988) oil formation volume factor correlation with new calculated coefficients.

Labedi (1990) presented correlations for oil formation volume factor for African crude oils. He used 97 data sets from Libya, 28 from Nigeria, and 4 from Angola to develop his correlations. Dokla and Osman (1992) published a set of correlations for estimating bubble point pressure and oil formation volume factor for UAE crudes. They used 51 data sets to calculate new coefficients for Al-Marhoun (1988) Middle East models. Al-Yousef and Al-Marhoun (1993) pointed out that the Dokla and Osman (1992, 1993) bubble point pressure correlation was found to contradict the physical laws. Al-Marhoun (1992) published a second correlation for oil formation volume factor. The correlation was developed with 11,728 experimentally obtained formation volume factors at, above, and below the bubble point pressure. The data set represents samples from more than 700 reservoirs from all over the world, mostly from Middle East and North America.

Macary and El-Batanoney (1992) presented correlations for bubble point pressure and oil formation volume factor. They used 90 data sets from 30 independent reservoirs in the Gulf of Suez to develop the correlations. The new correlations were tested against other Egyptian data of Saleh et al. (1987), and showed improvement over published correlations. Omar and Todd (1993) presented oil formation volume factor correlation, based on Standing’s (1947) model. Their correlation was based on 93 data sets from Malaysian oil reservoirs. Petrosky and Farshad (1993) developed new correlations for the Gulf of Mexico.

Kartoatmodjo and Schmidt (1994) used a global data bank to develop new correlations for all PVT properties. Data from 740 different crude oil samples gathered from all over the world provided 5392 data sets for correlation development. Almehaideb (1997) published a new set of correlations for UAE crudes using 62 data sets from UAE reservoirs. These correlations were developed for bubble point pressure and oil formation volume factor. The bubble point pressure correlation of Omar and Todd (1993) uses the oil formation volume factor as input in addition to oil gravity, gas gravity, solution gas oil ratio, and reservoir temperature. Saleh et al. (1987) evaluated the empirical correlations for Egyptian oils. They reported that Standing’s (1947) correlation was the best for oil formation volume factor. Sutton and Farshad (1990a, b) published an evaluation for Gulf of Mexico crude oils. They used 285 data sets for gas-saturated oil and 134 data sets for undersaturated oil representing 31 different crude oils and natural gas systems. The results show that Glaso (1980) correlation for oil formation volume factor perform the best for most of the data of the study. Later, Petrosky and Farshad (1993) published a new correlation based on the Gulf of Mexico crudes. They reported that the best performing published correlation for oil formation volume is the Al-Marhoun (1988) correlation. McCain (1991) published an evaluation of all reservoir properties correlations based on a large global database. He recommended Standing’s (1947) correlations for formation volume factor at and below the bubble point pressure.

Al-Fattah and Al-Marhoun (1994) published an evaluation of all available oil formation volume factor correlations. They used 674 data sets from published literature. They found that Al-Marhoun (1992) correlation has the least error for global data set. Also, they performed trend tests to evaluate the model’s physical behavior. Finally, Al-Shammasi (1997) evaluated the published correlations and neural network models for bubble point pressure and oil formation volume factor for accuracy and flexibility to represent hydrocarbon mixtures from different geographical locations worldwide. He presented a new correlation for bubble point pressure based on global data of 1661 published and 48 unpublished data sets. Also, he presented neural network models and compared their performance to numerical correlations. He concluded that statistical and trend performance analysis showed that some of the correlations violate the physical behavior of hydrocarbon fluid properties.

De Ghetto et al. (1994) performed a comprehensive study on PVT properties correlation based on 195 global data sets collected from the Mediterranean Basin, Africa, Middle East, and the North Sea reservoirs. They recommended Vazquez and Beggs (1980) correlation for the oil formation volume factor. Elsharkawy et al. (1994) evaluated the PVT correlations for Kuwaiti crude oils using 44 samples. Standing’s (1947) correlation gave the best results for bubble point pressure, while Al-Marhoun (1988) oil formation volume factor correlation performed satisfactorily.

Hanafy et al. (1997) published a study to evaluate the most accurate correlation to apply to Egyptian crude oils. For formation volume factor, Macary and El-Batanoney (1992) correlation showed an average absolute error of 4.9 %, while Dokla and Osman (1992) showed 3.9 %. The study strongly supports the approach of developing a local correlation versus a global correlation.

Mahmood and Al-Marhoun (1996) presented an evaluation of PVT correlations for Pakistani crude oils. They used 166 data sets from 22 different crude samples for the evaluation. Al-Marhoun (1992) oil formation volume factor correlation gave the best results. The bubble point pressure errors reported in this study, for all correlations, are among the highest reported in the literature. It is also possible to increase the accuracy by updating the coefficients of Al-Marhoun correlation, but it is not necessary that the update correlation captures nonlinear behavior completely. Therefore, Mahmood and Al-Marhoun (1996) also recommended new PVT correlations for Pakistani crude oils and this recommendation is the basis for this research.

Artificial neural network

Neural networks are composed of simple elements operating in parallel. These elements are inspired by biological nervous systems. We can train a neural network to perform a particular function by adjusting the values of the connections (weights) between elements. Typically, neural networks are adjusted, or trained, so that a particular input leads to a specific target output (MathWorks, Inc 2008).

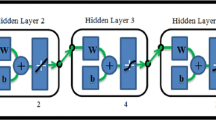
Neural network consists of input and output neurons (elements) and layers, which are connected by further neurons and layers known as hidden layer and hidden layer neurons (Fauset 1996). These neurons are connected in a highly parallel and distributed way, so that they can map any nonlinear complex function as shown in Fig. 1. Each connection in the neural network assigns weights and layers and are connected by transfer functions. The response from each neuron is given by

$$y_{j} = f\left( {\sum\limits_{i = 1}^{\text{Ni}} {w_{ji} { \times }x_{i} } + b_{j} } \right),$$

where x i are the input parameters, i is the index for input parameters, Ni is the total number of input parameters, j is the index for hidden layer neurons, b j  is the bias for hidden layer neuron j, y j  is the output of hidden layer neuron j, w ji  are weights between the input and hidden layer, f is the tan-sigmoid transfer functionand

$$z_{k} = f_{\text{L}} \left( {\sum\limits_{j = 1}^{\text{Nh}} {w_{jk} { \times }y_{j} } + b_{k} } \right).$$

In this, k is the index for a number of output parameters, b k  is the bias for the output layer, w jk  are the weights between the hidden and output layer, Nh is the total number of hidden layer neurons, z k  are the outputs of the output layer, and f L is the linear transfer function.

Fig. 1
figure 1

Generalized ANN model architecture with input, hidden, and output layer

Full size image

The work flow for the neural network design process has the following primary steps:

  • Collect data.

  • Create the network.

  • Configure the network.

  • Initialize the weights and biases.

  • Train and validate the network.

  • Test and use the network.

In recent years, neural networks have gained popularity in petroleum applications. Many authors have discussed the applications of neural network in petroleum engineering (Kumoluyi and Daltaban 1994; Ali 1994; Mohaghegh and Ameri 1994; Mohaghegh 1995). Few studies have been carried out to model the PVT properties using neural networks. Gharbi and Elsharkawy (1997) published neural network models for estimating bubble point pressure and oil formation volume factor for Middle East crude oils. Both neural network models were trained using 498 data sets collected from the literature and unpublished sources. The models were tested by other 22 data points from the Middle East. The results showed improvement over the conventional correlation methods with reduction in the average error for the bubble point pressure oil formation volume factor.

Varotsis et al. (1999) presented a novel approach for predicting the complete PVT behavior of reservoir oils and gas condensates using artificial neural network (ANN). The method uses key measurements that can be performed rapidly either in the laboratory or at the well site as input to an ANN. The ANN was trained by a PVT study database of over 650 reservoir fluids originating from all parts of the world. Tests of the trained ANN architecture utilizing a validation set of PVT studies indicate that, for all fluid types, most PVT property estimates can be obtained with a very low mean relative error of 0.5–2.5 %, with no data set having a relative error in excess of 5 %. Osman and Al-Marhoun (2002) developed PVT correlations using ANN for Saudi crude oils. The models were developed using 283 data sets, which were collected from Saudi Reservoirs. Gupta (2010) developed PVT correlations using artificial neural network for Indian crude oils. The models were developed using 372 data sets, which were collected from Indian reservoirs. All of the regional ANN PVT correlations outperform the previously published correlations. Mahmood and Al-Marhoun (1996) presented an evaluation of PVT correlations for Pakistani crude oils. In this study (Mahmood and Al-Marhoun 1996), they concluded that new PVT correlations for Pakistani crude oils are required and therefore this recommendation and conclusion are the basis for this research. Moreover due to the previous success of ANN in regional PVT correlations, ANN is used as an algorithm for PVT correlations of Pakistani crude oil.

Data acquisition and analysis

Data used for this work were collected from Mahmood and Al-Marhoun (1996) publication related to evaluation of PVT correlations for Pakistani crude oil. In general, this data set covers a wide range of bubble point pressure, oil FVF, solution gas/oil ratio, and gas relative density values; whereas the temperature and oil gravity belong to relatively higher values attributed to regional trends prevailing in Pakistani crude oils. Each data set contains reservoir temperature, oil gravity, total solution gas oil ratio, and average gas gravity, bubble point pressure, oil formation volume factor at the bubble point pressure, and viscosity at the bubble point pressure. The data set was randomly divided into two groups of seen data (70 % of total data) and unseen data (30 % of total data). Out of a total of 166 data points, 70 % (seen data by ANN) were used for training, validation, or cross-validation of the ANN models, the remaining 30 % (unseen data by ANN) were used to test the model to evaluate its accuracy. For viscosity at P b data, 128 data points are available in Mahmood and Al-Marhoun’s (1996) publication and these are divided in the same way as bubble point pressure and formation volume factor at P b . A statistical description of training (seen) and test (unseen) data are given in Tables 1 and 2, respectively.

Table 1 Statistical description of the input and output data used for training and cross-validation
Full size table
Table 2 Statistical description of the input and output data used for testing
Full size table

Bubble point pressure artificial neural network model

The bubble point pressure ANN model consists of four input neurons or input parameters, which are related to temperature, specific gravity of gas, API gravity of oil and solution gas–oil ratio, one hidden layer and one output neuron related to bubble point pressure. The hidden layer consists of 12 neurons, which were obtained after sensitivity runs of the number of neurons from 5 to 50. Tan-sigmoid and linear transfer functions were used in the hidden and output layer, respectively. The algorithm of ANN model for bubble point pressure is given below:

$$P_{b} = f_{\text{L}} \left( {\sum\limits_{j = 1}^{\text{Nh}} {w_{jk} { \times }\left( {f\left( {\sum\limits_{i = 1}^{\text{Ni}} {w_{ji} { \times }x_{i} } + b_{j} } \right)} \right)} + b_{k} } \right).$$

The above ANN algorithm for bubble point pressure can also be written in the following way:

$$\begin{aligned} (P_{b})_N &= f_{\text{L}} \left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times (T)_N + \, w_{j2} \times (\gamma_{g})_N + w_{j3} \times ({\text{API}})_N \right. \\ & \quad \left.\vphantom{\left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times T + \, w_{j2} \times \gamma_{g} + w_{j3} \times {\text{API}} \right.} + w_{j4} \times ({\text{Rs}})_N) + b_{j} \big) \big) + b_{k} \right).\end{aligned}$$

Subscript N shows the normalized input and output parameters for ANN model. The bias values are constant and have a similar concept to constants in linear or nonlinear regression. The architecture of the ANN model for bubble point pressure is shown in Fig. 2.

Fig. 2
figure 2

Architecture of ANN model for bubble point pressure

Full size image

To obtain weights and bias values, training of neural network was performed by Levenberg–Marquardt back-propagation algorithm. To avoid local minimum, 5000 multiple realizations with different weight and bias initialization of training were implemented and the minimum error realization was selected as the best one. After training, the optimal weights and bias values were obtained for bubble point pressure ANN and these are shown in Table 3.

Table 3 Weights and bias values for P b artificial neural network model
Full size table

All input parameters should be normalized in the range of [−1, 1] before using in the ANN algorithm for bubble point. The general equation for input normalization is given below:

$${\text{Input}}_{\text{norm}} = \frac{{\left( {{\text{Input}}_{ \hbox{max} } - {\text{Input}}_{ \hbox{min} } } \right)\left( {x - x_{ \hbox{min} } } \right)}}{{\left( {x_{ \hbox{max} } - x_{ \hbox{min} } } \right)}} + {\text{ Input}}_{ \hbox{min} } ,$$
$${\text{Input}}_{ \hbox{min} } = \, - 1,$$
$${\text{Input}}_{ \hbox{max} } = { 1} .$$

The x max and x min values (ranges of input parameters) are given in Table 1. Therefore, the input parameters should be normalized by using the following equations:

$$\left( T \right)_{N} = \frac{{2\left( {T - 182} \right)}}{{\left( {296 - 182} \right)}} - 1,$$
$$\left( {\gamma_{g} } \right)_{N} = \frac{{2\left( {\gamma_{g} - 0.825} \right)}}{{\left( {3.444 - 0.825} \right)}} - 1,$$
$$\left( {\text{API}} \right)_{N} = \frac{{2\left( {{\text{API}} - 29} \right)}}{{\left( {43.8 - 29} \right)}} - 1,$$
$$\left( {\text{Rs}} \right)_{N} = \frac{{2\left( {{\text{Rs}} - 92} \right)}}{{\left( {2496 - 92} \right)}} - 1.$$

The proposed ANN model gives normalized bubble point pressure in the range [−1, 1]; therefore for real value of the bubble point pressure, the output value should be de-normalized by the following equation:

$${\text{Output}} = \frac{{\left( {y_{ \hbox{max} } - y_{ \hbox{min} } } \right)\left( {{\text{Output}}_{\text{norm}} - ( - 1)} \right)}}{(1) - ( - 1)} + y_{ \hbox{min} } ,$$

where y max and y min values (minimum and maximum bubble point pressures) are given in Table 1. Therefore, the output parameter should be de-normalized by using following equation:

$$P_{b} = \frac{{\left( {4975 - 79} \right)\left( {(P_{b} )_{N} - ( - 1)} \right)}}{2} + 79.$$

Oil formation volume factor of the P b (B ob) ANN model

The oil formation volume factor of the P b ANN model consists of four input neurons or input parameters, which are related to temperature, specific gravity of gas, API gravity of oil and solution gas–oil ratio, one hidden layer and one output neuron related to B ob. The hidden layer consists of 8 neurons, which were obtained after sensitivity runs of number of neurons from 5 to 50. Tan-sigmoid and linear transfer functions were used in the hidden and output layer, respectively. The algorithm of the ANN model for B ob is given below:

$$B_{\text{ob}} = f_{\text{L}} \left( {\sum\limits_{j = 1}^{\text{Nh}} {w_{jk} { \times }\left( {f\left( {\sum\limits_{i = 1}^{\text{Ni}} {w_{ji} { \times }x_{i} } + b_{j} } \right)} \right)} + b_{k} } \right).$$

The above ANN algorithm for B ob can also be written in the following way:

$$\begin{aligned} (B_{\text{ob}})_N &= f_{\text{L}} \left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times (T)_N + \, w_{j2} \times (\gamma_{g})_N + w_{j3} \times ({\text{API}})_N \right. \\ &\quad \left.\vphantom{\left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times T + \, w_{j2} \times \gamma_{g} + w_{j3} \times {\text{API}} \right. } + w_{j4} \times ({\text{Rs}})_N) + b_{j} \big) \big) + b_{k} \right). \end{aligned}$$

Subscript N shows the normalized input and output parameters for ANN model. The bias values are constant values, which have a similar concept to constants in linear or nonlinear regression. The architecture of ANN model for B ob is shown in Fig. 3.

Fig. 3
figure 3

Architecture of ANN model for B ob

Full size image

To obtain weights and bias values, training of neural network was performed by Levenberg–Marquardt back-propagation algorithm. To avoid local minimum, 5000 multiple realizations with different weight and bias initialization of training were implemented and minimum error realization was selected as the best one. After training, the optimal weights and bias values were obtained for B ob artificial neural network and these are shown in Table 4.

Table 4 Weights and bias values for B ob artificial neural network model
Full size table

All input parameters should be normalized in the range of [−1, 1] before using in the ANN algorithm for B ob. The procedure for normalization of input parameters is the same as of bubble point ANN algorithm.

The input parameters should be normalized using the following equations for the ANN algorithm of B ob:

$$\left( T \right)_{N} = \frac{{2\left( {T - 182} \right)}}{{\left( {296 - 182} \right)}} - 1,$$
$$\left( {\gamma_{g} } \right)_{N} = \frac{{2\left( {\gamma_{g} - 0.825} \right)}}{{\left( {3.444 - 0.825} \right)}} - 1,$$
$$\left( {\text{API}} \right)_{N} = \frac{{2\left( {{\text{API}} - 29} \right)}}{{\left( {56.5 - 29} \right)}} - 1,$$
$$\left( {\text{Rs}} \right)_{N} = \frac{{2\left( {{\text{Rs}} - 96} \right)}}{{\left( {2496 - 96} \right)}} - 1.$$

The proposed ANN model gives normalized B ob in the range [−1, 1]; therefore for the real value of B ob, the output B ob value should be de-normalized by the following equation:

$$B_{\text{ob}} = \frac{{\left( {2.916 - 1.214} \right)\left( {(B_{\text{ob}} )_{N} - ( - 1)} \right)}}{2} + 1.214.$$

Viscosity in the P b (µ ob) ANN model

The viscosity in the P b ANN model consists of four input neurons or input parameters, which are related to temperature, specific gravity of gas, API gravity of oil and solution gas–oil ratio, one hidden layer and one output neuron related to µ ob. The hidden layer consists of 26 neurons, which were obtained after sensitivity runs of number of neurons from 5 to 50. Tan-sigmoid and linear transfer functions were used in the hidden and output layer, respectively. It is important to note that the hidden layer neurons in µ ob ANN model is higher than the bubble point and B ob ANN models, because nonlinearity in µ ob is higher than bubble point and B ob. The algorithm of the ANN model for µ ob is given below:

$$\mu_{\text{ob}} = f_{\text{L}} \left( {\sum\limits_{j = 1}^{\text{Nh}} {w_{jk} { \times }\left( {f\left( {\sum\limits_{i = 1}^{\text{Ni}} {w_{ji} { \times }x_{i} } + b_{j} } \right)} \right)} + b_{k} } \right).$$

The above ANN algorithm for µ ob can also be written in the following way:

$$\begin{aligned} (\mu_{\text{ob}})_N &= f_{\text{L}} \left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times (T)_N + \, w_{j2} \times (\gamma_{g})_N + w_{j3} \times ({\text{API}})_N \right. \\ & \quad \left. \vphantom{\left( \sum\limits_{j = 1}^{\text{Nh}} w_{jk} \times \big( f\big( w_{j1} \times T + \, w_{j2} \times \gamma_{g} + w_{j3} \times {\text{API}} \right.} + w_{j4} \times ({\text{Rs}})_N) + b_{j} \big) \big) + b_{k} \right). \end{aligned}$$

Subscript N shows the normalized input and output parameters for ANN model. The bias values are constant values, which have similar concept to constants in linear or nonlinear regression. The architecture of the ANN model for µ ob is shown in Fig. 4.

Fig. 4
figure 4

Architecture of ANN model for µ ob

Full size image

To obtain the weights and bias values, the training of neural network was performed by the Levenberg–Marquardt back-propagation algorithm. To avoid local minimum, 5000 multiple realizations with different weight and bias initialization of training were implemented and minimum error realization was selected as the best one. After training, the optimal weights and bias values were obtained for µ ob ANN and these are shown in Table 5.

Table 5 Weights and bias values for µ ob artificial neural network model
Full size table

All input parameters should be normalized in the range of [−1, 1] before using in the ANN algorithm for µ ob. The procedure for normalization of input parameters is the same as of bubble point pressure and B ob ANN algorithms.

The input parameters should be normalized using the following equations for the ANN algorithm of µ ob:

$$\left( T \right)_{N} = \frac{{2\left( {T - 188} \right)}}{{\left( {296 - 188} \right)}} - 1,$$
$$\left( {\gamma_{g} } \right)_{N} = \frac{{2\left( {\gamma_{g} - 0.825} \right)}}{{\left( {3.444 - 0.825} \right)}} - 1,$$
$$\left( {\text{API}} \right)_{N} = \frac{{2\left( {{\text{API}} - 29} \right)}}{{\left( {43.8 - 29} \right)}} - 1,$$
$$\left( {\text{Rs}} \right)_{N} = \frac{{2\left( {{\text{Rs}} - 92} \right)}}{{\left( {2496 - 92} \right)}} - 1.$$

The proposed ANN model gives normalized µ ob in the range [−1, 1]; therefore for real value of µ ob, output µ ob value should be de-normalized by the following equation:

$$\mu_{\text{ob}} = \frac{{\left( {0.636 - 0.205} \right)\left( {(\mu_{\text{ob}} )_{N} - ( - 1)} \right)}}{2} + 0.205.$$

Results and discussion

After training the neural network models for P b , B ob and µ ob, the models become ready for testing and evaluation. To perform this, the first training data set (seen data) and the second testing data set, which were not seen by the neural network during training, were used.

To compare the performance and accuracy of the neural network model of P b to other empirical correlations, five mostly used P b correlations were selected. These are those of Standing (1947), Vazquez and Beggs (1980), Glaso (1980), and Lasater (1958). The statistical results of the comparison are given in Table 6. The ANN model of P b outperforms all these empirical correlations.

Table 6 Statistical comparison of bubble point pressure correlations and proposed bubble point pressure ANN model
Full size table

To compare the performance and accuracy of the neural network model of B ob to other empirical correlations, five mostly used B ob correlations were selected. These are those of Standing (1947), Vazquez and Beggs (1980), Glaso (1980), and Al-Marhoun (1988, 1992). The statistical results of the comparison are given in Table 7. The ANN model of B ob outperforms all these empirical correlations.

Table 7 Statistical comparison of B ob correlations and the proposed B ob ANN model
Full size table

To compare the performance and accuracy of the neural network model of µ ob to other empirical correlations, four mostly used µ ob correlations were selected. These are those of Beggs and Robinson (1975), Chew and Connaly (1959), Khan et al. (1987), and Labedi (1992). The statistical results of the comparison are given in Table 8. The ANN model of µ ob outperforms all these empirical correlations.

Table 8 Statistical comparison of µ ob correlations and the proposed µ ob ANN model
Full size table

The proposed neural network models showed high accuracy in predicting the P b , B ob, and µ ob values, and achieved the lowest relative error, lowest absolute percent relative error, lowest minimum error, lowest maximum error, and lowest standard deviation of relative error.

Conclusion

  • A new ANN model was developed to predict the bubble point pressure, oil formation volume factor at P b , and viscosity at P b . The P b and B ob models were developed using 166 published data sets from the Pakistani crude oil samples. The µ ob model was developed using 128 published data sets from the Pakistani crude oil samples.

  • Out of the 166 data points, 70 % were used to train and cross-validate the ANN models for P b and B ob, and the remaining 30 % used to test the accuracy of P b and B ob models. Similarly, for the µ ob model, out of the 128 data points, 70 % were used to train and cross-validate the ANN model and the remaining 30 % used to test the µ ob accuracy.

  • The results show that the developed models provide better predictions and higher accuracy than the published empirical correlations and have the capability to fulfill the need of more accurate correlations for Pakistani crude oil. The present models provide predictions of P b , B ob, and µ ob with an absolute average percent error of 4.4250, 0.4975, and 2.99 %, respectively, to unseen (testing) data and correlation coefficient of 0.99789, 0.997, and 0.97022, respectively, to unseen (testing) data.