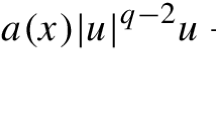Abstract
In this paper we study asymptotics as \(p\rightarrow \infty \) of the Dirichlet eigenvalue problem for the \(1\)-homogeneous \(p\)-Laplacian, that is,
Here \(\Omega \) is a bounded starshaped domain in \(\mathbb{R }^n\) and \(p>n\). There exists a principal eigenvalue \(\lambda _{1,p} (\Omega )\), which is positive, and has associated a non-negative nontrivial eigenfunction. Moreover, we show that \(\lim _{p\rightarrow \infty }\lambda _{1,p}(\Omega )= \lambda _{1,\infty }(\Omega ) \), where \(\lambda _{1,\infty }(\Omega )\) is the first eigenvalue corresponding to the \(1\)-homogeneous infinity Laplacian, that is, \( -\left( D^2u\frac{Du}{|Du|}\right) \cdot \frac{Du}{|Du|} =\lambda u\).
Similar content being viewed by others
References
Aronsson, G., Crandall, M.G., Juutinen, P.: A tour of the theory of absolutely minimizing functions. Bull. Am. Math. Soc. 41, 439–505 (2004)
Barles, G., Busca, J.: Existence and comparison results for fully nonlinear degenerate elliptic equations without zeroth-order term. Comm. Partial Differ. Equ. 26, 2323–2337 (2001)
Berestycki, H., Nirenberg, L., Varadhan, S.R.S.: The principal eigenvalue and maximum principle for second-order elliptic operators in general domains. Comm. Pure Appl. Math. 47, 47–92 (1994)
Birindelli, I., Demengel, F.: First eigenvalue and maximum principle for fully nonlinear singular operators. Adv. Differ. Equ. 11(1), 91–119 (2006)
Birindelli, I., Demengel, F.: Eigenvalue, maximum principle and regularity for fully non linear homogeneous operators. Commun. Pure Appl. Anal. 6(2), 335–366 (2007)
Charro, F., De Philippis, G., Di Castro, A., Máximo, D.: On the Aleksandrov-Bakelman- Pucci estimate for the infinity Laplacian. Calc. Var. PDE. (2013, to appear)
Crandall, M.G., Ishii, H., Lions, P.L.: User’s guide to viscosity solutions of second order partial differential equations. Bull. Am. Math. Soc. 27, 1–67 (1992)
Giga, Y.: Surface evolution equations. A level set approach. In: Monographs in Mathematics, vol. 99, Birkhäuser, Basel (2006)
Jensen, R.: Uniqueness of Lipschitz extensions: minimizing the sup norm of the gradient. Arch. Ration. Mech. Anal. 123, 51–74 (1993)
Juutinen, P.: Principal eigenvalue of a very badly degenerate operator and applications. J. Differ. Equ. 236, 532–550 (2007)
Juutinen, P., Lindqvist, P., Manfredi, J.J.: On the equivalence of viscosity solutions and weak solutions for a quasi-linear elliptic equation. SIAM J. Math. Anal. 33, 699–717 (2001)
Juutinen, P., Lindqvist, P., Manfredi, J.J.: The \(\infty \)-eigenvalue problem. Arch. Ration. Mech. Anal. 148, 89–105 (1999)
Leoni, G.: A first course in Sobolev spaces. In: Graduate Studies in Mathematics, vol. 105. American Mathematical Society, New York (2009)
Manfredi, J.J., Parviainen, M., Rossi, J.D.: An asymptotic mean value characterization of \(p\)-harmonic functions. Proc. Am. Math. Soc. 138, 881–889 (2010)
Manfredi, J.J., Parviainen, M., Rossi, J.D.: On the definition and properties of \(p\)-harmonious functions. Ann. Scuola Normale Sup. Pisa. XI(2), 215–241 (2012)
Martínez-Aparicio, P. J., Pérez-Llanos, M., Rossi, J. D.: The sublinear problem for the 1-homogeneous \(p\)-Laplacian. Proc. Amer. Math. Soc. (to appear)
Peres, Y., Pete, G., Somersielle, S.: Biased Tug-of-War, the biased infinity Laplacian and comparison with exponential cones. Calc. Var. PDE 38, 541–564 (2010)
Peres, Y., Schramm, O., Sheffield, S., Wilson, D.: Tug-of-war and the infinity Laplacian. J. Am. Math. Soc. 22, 167–210 (2009)
Peres, Y., Sheffield, S.: Tug-of-war with noise: a game theoretic view of the \(p\)-Laplacian. Duke Math. J. 145(1), 91–120 (2008)
Acknowledgments
The authors wish to thank to J. García-Azorero for his useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
P. J. Martínez-Aparicio supported by MICINN Ministerio de Ciencia e Innovación (Spain) MTM2012- 31799 and Junta de Andalucía FQM-116. M. Pérez-Llanos and J. D. Rossi supported by project MTM2010-18128 (Spain).
Rights and permissions
About this article
Cite this article
Martínez-Aparicio, P.J., Pérez-Llanos, M. & Rossi, J.D. The limit as \(p\rightarrow \infty \) for the eigenvalue problem of the 1-homogeneous \(p\)-Laplacian. Rev Mat Complut 27, 241–258 (2014). https://doi.org/10.1007/s13163-013-0124-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13163-013-0124-4