Modeling, Analysis and Simulations of a Dynamic Thermoviscoelastic Rod-Beam System

Abstract

This work models, analyses and simulates a coupled dynamic system consisting of a thermoviscoelastic rod and a linear viscoelastic beam. It is motivated by recent developments in MEMS systems, in particular the “V-shape” electro-thermal actuator that realizes large displacement and reliable contact in MEMS switches. The model consists of a system of three coupled partial differential equations for the beam’s and the rods’ displacements, and the rod’s temperature. Moreover, the rod may come in contact with a reactive foundation at one end, which is the main aspect of the actuating or switching property of the system. The thermal interaction at the contacting end of the rod is described by Barber’s heat exchange condition. The system is analyzed by setting it in an abstract form for which the existence of a weak solution is shown by using tools from the theory of variational inequalities and a fixed point theorem. A numerical algorithm for the system is constructed; its implementation yields computational depiction of the system’s behavior, with emphasis on the combined vibrations of the beam-rod system, dynamic contact force and thermal interaction.

A Appendix: Dimensionless System

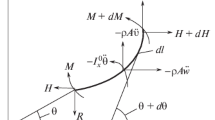
We describe the dimensional and dimensionless forms of the system. The full system, where the dimensional variables are with tildes, is as follows. The dynamic equation for the vibrations of the beam is

$$\begin{aligned} \rho _{b} \widetilde{w}_{\widetilde{t} \widetilde{t}}+k_{b}\widetilde{w}_{ \widetilde{x}\widetilde{x}\widetilde{x}\widetilde{x}} +\widetilde{\nu }_{b} w_{\widetilde{x}\widetilde{x}\widetilde{x}\widetilde{x}\widetilde{t}}= \widetilde{f}_{b}, \end{aligned}$$

the equation for the vibrations of the rod is

$$\begin{aligned} \rho _{d}\widetilde{u}_{\widetilde{t}\widetilde{t}}-k_{d}\widetilde{u}_{ \widetilde{y}\widetilde{y}} -\widetilde{\nu }_{d}\widetilde{u}_{\widetilde{y} \widetilde{y}\widetilde{t}}+\widetilde{\alpha } \theta _{amb}\widetilde{\theta } _{\widetilde{y}} =\widetilde{f}_{d}, \end{aligned}$$

and the heat conduction equation for the rod is

$$\begin{aligned} \rho _{d} \widetilde{c}_{th}\widetilde{\theta }_{\widetilde{t}}-\widetilde{ \kappa }_{th}\widetilde{\theta }_{\widetilde{y}\widetilde{y}} +\widetilde{ \alpha } \widetilde{u}_{\widetilde{y}\widetilde{t}}+\widetilde{h}_{d}\big ( \widetilde{\theta } -\theta _{amb}\big )=\widetilde{Q}_{d}. \end{aligned}$$

Here, $\widetilde{\theta }(\widetilde{t})$ is the absolute temperature of the rod and $\theta _{amb}$ is the ambient temperature, assumed to be constant; $\rho _{b}, \rho _{d}, k_{b}, k_{d}, \widetilde{\nu }_{b}$, and $\widetilde{\nu } _{d}$, are the densities (per unit length), the elastic coefficients, and the viscosity coefficients of the beam and rod, respectively. The rod’s thermal capacity is $\widetilde{c}_{th}$, the coefficient of heat conduction is $\widetilde{\kappa }_{th}$, and $\widetilde{\alpha }=\alpha ^* (3\lambda +2\mu )$ is its scaled coefficient of thermal expansion. Here, $\alpha ^*$ is the actual coefficient of thermal expansion and $\lambda$ and $\mu$ are the Lame coefficients of the rod. Also, $\widetilde{h}_{d}$ is the coefficient of heat exchange between the rod and the environment. Moreover, $\widetilde{f}_{b}$ and $\widetilde{f}_{d}$ are the (volume) forces acting of the beam and the rod (such as gravity), respectively, and $\widetilde{Q}_{d}$ is a heat source in the rod, such as heat generated by electric current.

We use, in addition to $x=\widetilde{x}/L_{b}$ and $y=\widetilde{y}/L_{b}$, the following dimensionless variables:

$$\begin{aligned} t=\frac{\widetilde{t}}{L_b}\sqrt{\frac{k_d}{\rho _d}},\quad w=\frac{ \widetilde{w}}{L_b}, \quad u=\frac{\widetilde{u}}{L_b}\quad \end{aligned}$$

and scale the temperature as

$$\begin{aligned} \theta (y, t)=\frac{\widetilde{\theta }\big (\widetilde{y}, \widetilde{t}\big ) -\theta _{amb}}{\theta _{amb}} -\frac{(l-y)}{l}\frac{\big (\widetilde{\theta }_{e} \big (\widetilde{t\big )}-\theta _{amb}\big )}{\theta _{amb}} \end{aligned}$$

where $\widetilde{\theta }_{e}(\widetilde{t)}$ is the absolute temperature applied at the junction $y=0$. This scaling is such that $\theta (0,t)=0$ which helps with some of the mathematical manipulations below.

Next, we let

$$\begin{aligned} c_{b}^{2}=\frac{k_{b}\rho _{d}}{L^{2}_{b}\rho _{b}k_{d}},\qquad \nu _{b}=\frac{ \widetilde{\nu }_{b}}{\rho _{b}L^{3}_{b}}\sqrt{\frac{\rho _{d}}{k_{d}}},\quad \nu _d= \frac{\widetilde{\nu }_{d}}{L_{b}\sqrt{\rho _{d} k_{d}}}, \end{aligned}$$

and

$$\begin{aligned}&\alpha = \frac{\widetilde{\alpha } \theta _{amb}}{L_{b}},\qquad h_{d} = \widetilde{h_d}\theta _{amb} \sqrt{\frac{\rho _d}{k_d}},\qquad \kappa _{th}=\frac{\widetilde{\kappa }_{th} \theta _{amb}}{L_{b}^{2}} \sqrt{\frac{ \rho _d}{k_d}},\\&\quad c_{th}= \frac{\rho _d \widetilde{c}_{th}\theta _{amb}}{ L_{b}}. \end{aligned}$$

Finally, we set

$$\begin{aligned} f_{b}(x, t)= & {} \frac{L_{b}\rho _{d}}{k_{d}} \widetilde{f}_{b}\big (\widetilde{x}, \widetilde{t}\big ),\\ f_{d}(y, t)= & {} \frac{L_{b}}{k_{d}}\widetilde{f}_{d}(\widetilde{y}, \widetilde{t} )+ \frac{\widetilde{\alpha }L_{b} \big (\widetilde{\theta }_{e}\big (\widetilde{t\big )} -\theta _{amb}\big )}{k_{d} L_{d}}, \end{aligned}$$

and

$$\begin{aligned} Q_{d}(y, t)=\sqrt{\frac{ \rho _d}{k_d}}\widetilde{Q}_{d}- \sqrt{\frac{ \rho _d}{k_d}}\frac{(l-y)}{ l} \left( \widetilde{c}_{th}\dot{\widetilde{\theta }}_{e} - \widetilde{h}_{d} (\widetilde{\theta }(\widetilde{t}) -\theta _{amb}) \right) , \end{aligned}$$

where the dot represents the time derivative.

The dimensionless systems that results is

$$\begin{aligned} w_{tt}+c^{2}_{b}w_{xxxx}+\nu _{b}w_{xxxxt}=f_{b}, \end{aligned}$$

the equation for the vibrations of the rod is

$$\begin{aligned} u_{tt}-u_{yy}-\nu _{d}u_{yyt}+\alpha \theta _{y}=f_{d}, \end{aligned}$$

and the heat conduction equation for the rod is

$$\begin{aligned} c_{th}\theta _{t}-\kappa _{th}\theta _{yy}+\alpha u_{yt}+h_{d}\theta =Q_{d}. \end{aligned}$$

The last part is to set the heat exchange condition in a dimensionless form. The dimensional condition at $y=l$ is

$$\begin{aligned} - \widetilde{\kappa }_{th}\widetilde{\theta }_{\widetilde{y}} =\widetilde{ h} _{NC} \big (\widetilde{\theta } - \theta _{amb}\big ). \end{aligned}$$

Hence, if we set $r(t)=\widetilde{r}(\widetilde{t)}/L_{b}$, we find

$$\begin{aligned} q(r, t)=\big ( \widetilde{\kappa }_{th} - \widetilde{ h}_{NC}(\widetilde{r} )(l-y)\big )\frac{\big (\widetilde{\theta }_{e}(t) -\theta _{amb}\big )}{l\,L_{b}}, \end{aligned}$$

and also

$$\begin{aligned} h_{NC}(r(t))= \frac{\widetilde{ h}_{NC}\big (\widetilde{r}(\widetilde{t)}\big )}{L_{b}}, \end{aligned}$$

we obtain the heat exchange condition at $y=l$,

$$\begin{aligned} -\kappa _{th}\theta _{y} =h_{NC}(r) \theta -q(r). \end{aligned}$$

We note that the assumptions on the problem data

$$\begin{aligned} {\mathbf {f}}=(f_{d}, f_{b}) \in L^{2}\left( 0,T: H \times H_{0}\right) , \qquad Q_{d}\in L^{2}( 0,T: H_{0}), \end{aligned}$$

and

$$\begin{aligned} h_{NC}, q \in C^{1},\qquad |h_{NC}'|, |q'|\le C_{h}, \end{aligned}$$

are very reasonable from the point of view of applications. Moreover, they imply that the normal compliance function has at most linear growth. We note that if we assume that $h_{NC}$ is Lipschitz, the theorem still holds true.