Abstract
When too few photons reach detector elements, strong streaks appear through paths of high X-ray attenuation and an image becomes completely useless. This photon starvation artifact phenomenon occurs frequently when a pelvis or shoulder is scanned with thin slices. The common understanding regarding photon starvation streaks is that they are a manifestation of irregularities caused by noise in the raw data profile. Therefore, the common countermeasure is local raw-data filtering, which detects and smoothes out the highly noisy part of the raw data. However, the photon starvation artifact can be solved only partly with such a method and a more effective solution is necessary. Here, we examined the mean level shift of raw data attributable to the nonlinear nature of logarithmic conversion, which is the process required for generating raw data from detected X-ray data. We judge that the real culprit of the photon starvation artifact is this mean level shift. When the noise level is very high or the photon level is very low, this mean level shift can become prominent and can become manifest as thick streaks against which the conventional local raw data filtering has no power. To solve this problem, we propose a new scheme of local raw data filtering, which consists of reverting log-converted raw data to a form that is equivalent to pre-log detector data. With this method, not only fine streaks, but also thick streaks are removed effectively. A better image quality with lower X-ray doses is possible with this method.







Similar content being viewed by others
References
Hsieh J. Adaptive streak artifact reduction in computed tomography resulting from excessive x-ray photon noise. Med Phys. 1998;25(11):2139–47.
Hsieh J. Generalized adaptive median filters and their application in computed tomography. Proc SPIE. 1994;2298:662–72.
Kachelriess M, Watzke O, Kalender W. Generalized multi-dimensional adaptive filtering for conventional and spiral single-slice, multislice, and cone-beam CT. Med Phys. 2001;28(4):475–90.
Yang Z, Zamyatin A, Akino N. Effective data-domain noise and streak reduction for X-ray CT. In: Fully 3D 2011 Proceedings; 2011. p. 290–3.
Shi D, Zou Y, Zamyatin A. Weighted simultaneous algebraic reconstruction technique. In: Fully 3D 2011 Proceedings; 2011. p. 2139–47.
Rivière P. Penalized-likelihood sinogram smoothing for low-dose CT. Med Phys. 2005;32(6):1676–83.
Wang J, Li T, Lu H, et al. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography. IEEE Trans Med. 2006;25(10):1272–83.
Mori I, Kazama M. Method for suppressing streak artifacts in CT resulting from excessive noise. Med Imaging Technol. 2003;21(4):272–6.
Iwamoto S, Shiozaki A. Correction of nonlinear projection in photon shortage condition of X-ray CT using together adaptive filter. IEICE Technical Report MI2005; 105(580):17–20.
Iwamoto S, Shiozaki A. Statistical influence of logarithmic transform of projection data with noise and a simple correction method. Med Imaging Technol. 2006;24(3):209–15.
Mori I, Machida Y, Yamagata H. CT and MRI. San Antonio: Corona Publishing; 2010. p. 53–5.
Williamson J, Whiting B, Benak J, et al. Prospects for quantitative CT imaging. Med Phys. 2002;29(10):2404–18.
Bracewell R. The Fourier transform and its application. 3rd ed. New York: McGraw-Hill; 1999. p. 186–90.
Joseph P, Spital R, Stockham C. The effects of sampling on CT images. Comput Tomogr. 1980;4(3):189–206.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Statistics of raw data processed by local filtering
For analysis, we assume that x and p are uniform within the support of filter, except for the variation attributable to noise. The filter dimension might be 2 or 3, but we use its flattened one-dimensional expression f m , whose number of elements is M.
1.1 Conventional LRF
The mean level of processed raw data p′ is the same as that of untreated raw data:
The variance of p′ is
By use of Eq. (6) of the main text, the above can be rewritten as
1.2 Idealistic LRF
We first consider the statistics of an intermediate variable y, which is the filtered x. The iLRF handles non-clamped x, and not x c .
The mean level is unchanged:
According to the central limit theorem [13], the probability density distribution of y approaches a Gaussian distribution no matter how the x is distributed. The variance of y is the weighted sum of the variance of x:
Therefore, the mean and variance of the filtered raw data p′ is the following, by definition:
However, the system constant C in Eq. (20) is irrelevant for the variance. Therefore,
1.3 Reverted LRF
Although the choice of K does not affect the result, we now use the system constant K s for K. The reverted value x′ is the following:
The mean and variance of x′ involve the integral of the probability density function of x:
The filtered value x” is
We now need the probability density distribution of x″. Again, according to the central limit theorem, it can be well approximated by a Gaussian distribution.
The mean and variance of the final raw data p′ are as follows:
Appendix 2: Choice of Gaussian filter
The conventional understanding of PS is such that irregularities of raw data attributable to noise constitute fine streaks in an image. Therefore, we want to seek the most appropriate filter shape to suppress fine streaks because of irregularities, although our intention in this paper is to assert that the mean level shift caused by noise is also important. For minimizing the amplitude of fine streaks, the noise amplitude after, not before, the convolution correction must be minimized.
We analyze the filter profile for the ray direction only because the convolution correction is in the ray direction. The local raw data p are first smoothed by filter h and then convolved by the convolution kernel c before back-projection. For both h and c, we assume symmetric profiles. We take the case of a five-point filter for h to show a computational example. For c, we use only seven central points. Beyond that, the sidelobe of c is virtually zero and is thus negligible.
Then t is the following, where h 0 is replaced by 1 − 2(h 1 + h 2) because of the constraint that the total of h is unity:
The variance of the convolution-corrected p c ′ is
Solving a system of differential equations, we can obtain h 1 and h 2 as functions of c which minimize the variance above.
Although the mathematical solution of the above differential equations is simple in form, it is too lengthy to write here. Instead, below is the numerical result when c is the Shepp–Logan convolution kernel:
This five-point h and its Gaussian fitting are shown in Fig. 8 together with cases of three points and seven points. In all cases, the optimal profile can be approximated well by a Gaussian. Regarding the use of convolution kernels other than the Shepp–Logan type, again the details are omitted here, but they also result in nearly a Gaussian h. Therefore, we conclude that a Gaussian filter is nearly optimal for suppression of fine streak.
We next want to discuss briefly whether the filter for LRF should be one-dimensional (ray direction only) or two-dimensional (view direction also). For conventional LRF applied to post-log raw data, the use of a two-dimensional filter was reported [3], but its efficacy was not shown. We presume that a one-dimensional filter was sufficient for conventional LRF, because backprojection is merely the superposition of plural neighboring views onto the same pixel, except for the peripheral area of an image and its effect is tantamount to view-directional filtering on a sinogram. In contrast, a one-dimensional filter was tried for pre-log LRF [1]. In this case, we presume that a two-dimensional filter should have been more effective as follows: the noise fluctuation range of pre-log data means the used range of the log conversion curve. A small range of a curve can be well approximated by a line segment, but the use of a wide range of a curve involves nonlinearity. Consequently, the noise fluctuation range of the pre-log data should be minimized to minimize both the noise amplification and the mean level shift. For that, we need to add view-directional filtering. By the same token, the use of two-dimensional filters is important for our rLRF and iLRF. The filter profile for view direction can be almost arbitrary. However, partly for simplicity and partly because such an isotropic Gaussian filter is intuitively natural and clean, we adopt the ray-directional Gaussian profile for the view direction also.
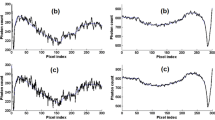
Our choice of an isotropic Gaussian filter can be justified by comparison with a two-dimensional boxcar (flat-square) filter, which is simple and which might be in use for conventional LRF of some CT scanners. Figure 9 is the point-spread function (PSF) of simulation images with use of a strong 7 × 7 Gaussian filter and a boxcar filter. In this case, noiseless raw data of a wire scan are used and the entire, not local, raw data are filtered. The PSF of the boxcar filter has an unnatural dent in the center, like a volcano. This phenomenon corresponds to the artifact which occurs when the raw data blur in a ray direction is too large compared with the sharpness of the image reconstruction kernel [14]. We have some concern that LRF by use of the boxcar filter might be accompanied by some subtle artifact of this type. The PSF of the Gaussian filter is natural in shape. The full-width half maximum (FWHM) of the line spread function obtained from the PSF is 3.15 mm for the Gaussian filter and 4.01 mm for the boxcar filter. The image noise was also compared with use of objectless (flat), but noisy raw data. The standard deviation of the CT number was 6.0 for the Gaussian filter and 6.5 for the boxcar filter.
Simulation conditions for the above PSF and noise experiments are: raw data generation and image reconstruction were done by PC with use of the C-language program. The convolution kernel was of the Shepp–Logan type. All other system geometries and parameters for simulation were identical to those of the actual CT machine, which is described in the main text.
In conclusion, in terms of sharpness, noise suppression, and naturalness of the PSF shape, the Gaussian filter is preferable to the boxcar filter.
About this article
Cite this article
Mori, I., Machida, Y., Osanai, M. et al. Photon starvation artifacts of X-ray CT: their true cause and a solution. Radiol Phys Technol 6, 130–141 (2013). https://doi.org/10.1007/s12194-012-0179-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12194-012-0179-9