Dynamics of hybrid switching diffusions SIRS model

Abstract

The main aim of this paper is to study the effect of the environmental noises in the asymptotic properties of a stochastic version of the classical SIRS epidemic model. The model studied here include white noise and telegraph noise modeled by Markovian switching. We obtained conditions for extinction both in probability one and in pth moment. We also established the persistence of disease under different conditions on the intensities of noises, the parameters of the model and the stationary distribution of the Markov chain. The highlight point of our work is that our conditions are sufficient and almost necessary for extinction and persistence of the epidemic. The presented results are demonstrated by numerical simulations.

1 Introduction

In recent years, mathematical models have been used increasingly to support public health policy making in the field of infectious disease control. The first roots of mathematical modeling date back to the eighteenth century, when Bernoulli [1] used mathematical methods to estimate the impact of smallpox vaccination on life expectancy. However, a rigorous mathematical framework was first worked out by Kermack and Mckendrick [2]. Their model, nowadays best known as the SIR model, has been the basis of all further modeling [3–6]. The SIR epidemic model, classifies individuals as one of susceptible, infectious and removed with permanent acquired immunity. In fact, some removed individuals lose immunity and return to the susceptible compartment. This case can be modeled by SIRS epidemic model studied by many scholars (see, e.g., [3, 7] and the references cited therein). For a fixed population size, let S(t) be the frequency of susceptible individuals, I(t) be the frequency of infective individuals and R(t) be the frequency of removed individuals at time t. A simple SIRS epidemic model is described by the following differential system:

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)=\left[ \mu -\mu S(t)-\beta S(t)I(t)+\gamma R(t)\right] dt, \\ dI(t)=\left[ -(\mu +\lambda )I(t)+\beta S(t)I(t) \right] dt,\\ dR(t)=\left[ -(\mu +\gamma )R(t)+\lambda I(t)\right] dt,\\ \end{array} \right. \end{aligned}$$

(1)

The meaning of parameters is as follows: $\mu$ represents the birth and death rates, $\beta$ is the infection coefficient, $\lambda$ is the recovery rate of the infective individuals, $\gamma$ is the rate at which recovered individuals lose immunity and return to the susceptible class. The dynamics of system (1) has been discussed in [3] in terms of the basic reproduction number $\mathcal {R}_0=\frac{\beta }{\mu +\lambda }$. It is shown that if $\mathcal {R}_0 \le 1$, the free-disease equilibrium state $E_0\left( 1,0,0\right)$ is globally asymptotically stable. while $\mathcal {R}_0>1$, $E_0$ becomes unstable and there exists an endemic equilibrium state $E_*\left( \frac{1}{\mathcal {R}_0},\frac{(\mu +\lambda )(\mu +\gamma )(\mathcal {R}_0-1)}{\beta (\mu +\lambda +\gamma )},\frac{\lambda (\mu +\lambda )(\mathcal {R}_0-1)}{\beta (\mu +\lambda +\gamma )}\right)$ which is globally asymptotically stable.

In real situation, parameters involved with the model are not absolute constants and always fluctuate randomly around some average value due to continuous fluctuation in the environment. Hence equilibrium distributions obtained from the deterministic analysis are not realistic rather they fluctuate randomly around some average value. Lu [8] introduced stochasticity into the SIRS model (1) via the technique of parameter perturbation. He replaced the infection coefficient $\beta$ by $\beta +\sigma \frac{dB}{dt}$, where B is a Brownian motion defined on the complete probability space $(\Omega ,\mathcal {F}, \{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ with a filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions and $\sigma$ is the intensity of the noise. So, the stochastic version of the deterministic system (1) is

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)=\left[ \mu -\mu S(t)-\beta S(t)I(t)+\gamma R(t)\right] dt-\sigma S(t)I(t)dB_t, \\ dI(t)=\left[ -(\mu +\lambda )I(t)+\beta S(t)I(t) \right] dt+\sigma S(t)I(t)dB_t,\\ dR(t)=\left[ -(\mu +\gamma )R(t)+\lambda I(t)\right] dt.\\ \end{array} \right. \end{aligned}$$

(2)

Lu [8] showed the local stability in probability of the disease-free equilibrium $E_0$ under the condition

$$\begin{aligned} \beta -(\mu +\lambda )+\frac{1}{2}\sigma ^2<0. \end{aligned}$$

(3)

Lahrouz et al. [9] improved the model (2) by supposing the saturated incidence rate $\frac{\beta SI}{1+a I}$ and disease-inflicted mortality. They proved the uniqueness and positivity of the solution and showed that the condition (3) is sufficient for the global stability in probability of $E_0$. they also established condition for the global stability in pth moment of $E_0$. Recently, in [10], Lahrouz and Settati found the threshold between persistence and extinction of the disease from the population. The technique of parameter perturbation has been used by many scholars (see, e.g., [11–13] and the references cited therein). However, this is not the only way to introduce stochasticity into the deterministic model (2).

There is another type of environmental noise, namely color noise, say telegraph noise [14–18]. Telegraph noise can be illustrated as a switching between two or more regimes of environment, which differ by factors such as nutrition, climatic characteristics or socio-cultural factorsfactors. The latter may cause the disease to spread faster or slower. Frequently, the switching among different environments is memoryless and the waiting time for the next switch is exponentially distributed. The regime-switching can hence be modeled by a finite-state Markov chain. Let r(t) be Markov chain defined in a finite state space $\mathbb {S}=\{1,2,\ldots ,m\}$ with the generator $\Theta =(\theta _{uv})_{1\le u,v\le m}$ given, for $\delta >0$, by

$$\begin{aligned} \mathbb {P}\left( r(t+\delta )=v|r(t)=u\right) ={\left\{ \begin{array}{ll}\theta _{uv}\delta +o(\delta ), &{}\,\, \text{ if }\,\,\, u\ne v,\\ 1+\theta _{uu}\delta +o(\delta ), &{}\,\, \text{ if }\,\,\, u= v.\, \end{array}\right. } \end{aligned}$$

(4)

Here, $\theta _{uv}$ is the transition rate from u to v while

$$\begin{aligned} \theta _{uu}=-\sum _{u\ne v}\theta _{uv}. \end{aligned}$$

(5)

In this paper, we set up a stochastic SIRS model in random environments using the following stochastic differential equation under regime switching:

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)=\left[ \mu _{r(t)}-\mu _{r(t)} S(t)-\beta _{r(t)} S(t)I(t)+\gamma _{r(t)} R(t)\right] dt-\sigma _{r(t)} S(t)I(t)dB_t, \\ dI(t)=\left[ -(\mu _{r(t)}+\lambda _{r(t)})I(t)+\beta _{r(t)} S(t)I(t) \right] dt+\sigma _{r(t)} S(t)I(t)dB_t,\\ dR(t)=\left[ -(\mu _{r(t)}+\gamma _{r(t)} )R(t)+\lambda _{r(t)} I(t)\right] dt.\\ \end{array} \right. \end{aligned}$$

(6)

The mechanism of the SIRS epidemic model described by system (6) can be explained as follows: Assume that initially, the Markov chain $r(0)=i\in \mathbb {S}$, then the model (6) satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)=\left[ \mu _i-\mu _i S(t)-\beta _i S(t)I(t)+\gamma _i R(t)\right] dt-\sigma _i S(t)I(t)dB_t, \\ dI(t)=\left[ -(\mu _i+\lambda _i)I(t)+\beta _i S(t)I(t) \right] dt+\sigma _i S(t)I(t)dB_t,\\ dR(t)=\left[ -(\mu _i+\gamma _i )R(t)+\lambda _i I(t)\right] dt,\\ \end{array} \right. \end{aligned}$$

until r(t) jumps to another state, say, $j\in \mathbb {S}$. Then the model obeys

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)=\left[ \mu _j-\mu _j S(t)-\beta _j S(t)I(t)+\gamma _j R(t)\right] dt-\sigma _j S(t)I(t)dB_t, \\ dI(t)=\left[ -(\mu _j+\lambda _j)I(t)+\beta _j S(t)I(t) \right] dt+\sigma _j S(t)I(t)dB_t,\\ dR(t)=\left[ -(\mu _j+\gamma _j )R(t)+\lambda _j I(t)\right] dt,\\ \end{array} \right. \end{aligned}$$

for a random amount of time until r(t) jumps to a new state again.

Since system (6) describes an epidemic model, it is critical to find out when the epidemic die out from the population and when does not. As far as we know, there are no persistent and extinction results for system (6). The aim of this work is to investigate this problem. The remainder of the paper is organized as follows: In Sects. 2, 3 and 4, we study the extinction case of the SDE model (6) under different types of convergence. In Sects. 5 and 6, we prove that the non-linear SDE (6) is persistent under certain parametric conditions. In Sect. 7, we introduce numerical simulations to illustrate the main results. Finally, we close the paper with conclusions and future directions.

2 The global stability of the disease-free equilibrium state

In this section, we will discuss the extinction of SDE system (6) in order to provide the threshold condition for disease control or eradication. We introduce the notation

$$\begin{aligned} \mathbb {R}_+^3=\left\{ (x_1,x_2,x_3)|x_i>0,\,i=1,2,3\right\} . \end{aligned}$$

To begin the analysis of the model, define the subset

$$\begin{aligned} \Delta =\left\{ x\in \mathbb {R}_{+}^{3};\,x_{1}+x_{2}+x_{3}=1\right\} . \end{aligned}$$

System (6) can be written as the following form:

$$\begin{aligned} dX(t)=f(X(t),r(t))dt+g(X(t),r(t))dB_t, \end{aligned}$$

(7)

where $X(t)=\left( S(t),I(t),R(t)\right)$, B is a Brownian motion defined on the complete probability space $(\Omega ,\mathcal {F}, \{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ and $(r(t))_{t\ge 0}$ is a right-continuous Markov chain defined on the same probability space, taking values in the finite state space $\mathbb {S}=\{1,2,\ldots ,m\}$ and having the generator $\Theta =(\theta _{uv})_{1\le u,v\le m}$ defined as in (4) and (5). With the reference to Zhu and Yin [19], the diffusion matrix is defined, for each $j\in \mathbb {S}$ by

$$\begin{aligned} G(X,j)=g(X,j)g^T(X,j) \end{aligned}$$

(8)

For use in rest of this paper, we introduce the generator $\mathcal {L}$ associated with (7) as follows. For each $j\in \mathbb {S}$, and for any twice continuously differentiable V(y, j),

$$\begin{aligned} \mathcal {L}V(X,j)= & {} f^T(X,j).\nabla V(y,j)+\frac{1}{2}Tr\left( g^T(X,j).\nabla ^2V(y,j).g(X,j)\right) \nonumber \\&+\,\Theta (y)V(y,.)(j), \end{aligned}$$

where

$$\begin{aligned} \Theta (y)V(y,.)(j)=\sum _{k\ne j,k\in \mathbb {S} }\theta _{jk}\left( V(y,k)-V(y,j)\right) . \end{aligned}$$

To ensure that the model is well posed and thus biologically meaningful, we need to prove that the solution remains in $\Delta$. By the similar proof of Theorem 2.1 in [20] or Theorem 2 in [9], we have the following theorem:

Theorem 2.1

The set $\Delta$ is almost surely positively invariant by the system (6), that is, if $\left( S(0),I(0),R(0)\right) \in \Delta ,$ then $\mathbb {P}\left( \left( S(t),I(t),R(t)\right) \in \Delta \right) =1$ for all $t\ge 0.$

With reference to Khasminskii et al. [21] and Yuan and Mao [22], we have the following lemma giving sufficient condition for asymptotical stability in probability in term of Lyapunov fuctions. We refer to Khasminskii et al. [21] for the precise meaning of asymptotical stability in probability.

Lemma 2.1

Assume that that there are functions $V\in \mathcal {C}^2\left( \mathbb {R}^3\times \mathbb {S};\mathbb {R}^+\right)$ and $w\in \left( \mathbb {R}^3;\mathbb {R}^+\right)$ vanishes only at $E_0$ such that

$$\begin{aligned} \mathcal {L}V(x,j)\le -w(x) \quad \quad \forall (x,j)\in \mathbb {R}^3\times \mathbb {S}, \end{aligned}$$

(9)

and

$$\begin{aligned} \underset{|x|\rightarrow \infty }{\lim }\underset{j\in \mathbb {S}}{\inf }V(x,j)=\infty . \end{aligned}$$

(10)

Then the equilibrium $E_0$ of the system (6) is globally asymptotically stable in probability.

In what follows, we shall give a condition for extinction of disease expressed in terms of the parameters of the model. To begin with, let us define the following quantities. For all $x\in \mathbb {R}$ and $j\in \mathbb {S}$,

$$\begin{aligned} A_j(x)=-\frac{1}{2}\sigma _{j}^{2}x^{2}+\beta _j x-(\mu _{j}+\alpha _{j}),\,\,\, \text{ and }\,\,\, C_{j}=A_j(1)=\beta _{j}-\mu _{j}-\lambda _{j} -\frac{1}{2}\sigma _{j}^{2}.\nonumber \\ \end{aligned}$$

(11)

Theorem 2.2

For any initial values $(S_{0},I_{0}, R_{0})\in \Delta$. If $\beta _{j}\ge \sigma _{j}^{2}$ for all $j\in \mathbb {S}$, and

$$\begin{aligned} \sum _{j=1}^m\pi _j C_{j} <0, \end{aligned}$$

(12)

then the disease-free $E_{0}$ of system (6) is globally asymptotically stable in probability.

Proof

Let $\left( S(0),I(0),R(0)\right) \in \Delta$. Let us define the Lyapunov functions

$$\begin{aligned} V_{1}(S,I,R,j) = \omega _{1}(1-S)^2+(\kappa + a_{j})I^{\frac{1}{\kappa }}+\omega _{2}R^2, \,\,\,j\in \mathbb {S}, \end{aligned}$$

(13)

where $\omega _{1}$, $\kappa$, $\omega _{2}$ and $a_{j}$ are real positive constants to be chosen in the following. We have

$$\begin{aligned} \mathcal {L}V_{1}= & {} -2\omega _{1}\mu _{j}(1-S)^2+2\omega _{1}\beta _{j}SI(1-S) -2\omega _{1}\gamma _{j}R(1-S)\\&+\,\omega _{1}\sigma _{j}^{2}S^2I^2-\frac{1}{\kappa }(\kappa + a_{j})(\mu _{j}+\lambda _{j})I^{\frac{1}{\kappa }} +\frac{1}{\kappa }(\kappa + a_{j})\beta _{j}SI^{\frac{1}{\kappa }}\\&+\,\frac{1}{2\kappa }\left( \frac{1}{\kappa }-1\right) (\kappa + a_{j})\sigma _{j}^{2}S^2I^{\frac{1}{\kappa }} -2\omega _{2}(\mu _{j}+\gamma _{j})R^{2}+2\omega _{2}\lambda _{j}IR\\ \\&+\,I^{\frac{1}{\kappa }}\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(a_k-a_j). \end{aligned}$$

Since $S,I\in (0,1)$ and $I\le 1-S$, we have, for all $\kappa \ge 1$,

$$\begin{aligned} \mathcal {L}V_{1}\le & {} -2\omega _{1}\mu _{j}(1-S)^2+2\omega _{1}\beta _{j}I^{\frac{1}{\kappa }} +\omega _{1}\sigma _{j}^{2}I^{\frac{1}{\kappa }}\\&-\,\frac{1}{\kappa }(\kappa + a_{j})(\mu _{j}+\lambda _{j})I^{\frac{1}{\kappa }}+ \frac{1}{\kappa }(\kappa + a_{j})\beta _{j}SI^{\frac{1}{\kappa }}\\&+\,\frac{1}{2\kappa }\left( \frac{1}{\kappa }-1\right) (\kappa + a_{j})\sigma _{j}^{2}S^{2}I^{\frac{1}{\kappa }}-2\omega _{2}(\mu _{j}+\gamma _{j})R^{2}\\&+\,2(\omega _{2}\lambda _{j}-\omega _{1}\gamma _{j})IR +I^{\frac{1}{\kappa }}\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(a_k-a_j). \end{aligned}$$

Hence, by choosing $\omega _{2}<\min _{j\in \mathbb {S}}\left\{ \frac{\omega _{1}\gamma _{j}}{\lambda _{j}}\right\} ,$ we get, for $\kappa \ge 1$,

$$\begin{aligned} \mathcal {L}V_{1}\le & {} -2\omega _{1}\mu _{j}(1-S)^2 -2\omega _{2}(\mu _{j}+\gamma _{j})R^{2} +\frac{1}{\kappa }(\kappa + a_{j})I^{\frac{1}{\kappa }}\Bigg ( \frac{\kappa \omega _{1}}{\kappa + a_{j}}(2\beta _{j}+\sigma _{j}^{2})\\&+\, \frac{1}{2\kappa }\sigma _{j}^{2}+ A_{j}(S)+ \frac{\kappa }{ \kappa + a_{j}}\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}\left( a_k-a_j\right) \Bigg ), \end{aligned}$$

where the functions $A_{j}$ are defined in (11). One can easily show, that if $\beta _{j}\ge \sigma _{j}^{2}$ then the functions $A_{j}$ are all increasing on (0,1), which means $A_{j}(S)\le A_{j}(1)$ and then

$$\begin{aligned} \nonumber \mathcal {L}V_{1}\le & {} -2\omega _{1}\mu _{j}(1-S)^2 -2\omega _{2}(\mu _{j}+\gamma _{j})R^{2} +\frac{1}{\kappa }(\kappa + a_{j})I^{\frac{1}{\kappa }}\left( \frac{\kappa \omega _{1}}{\kappa + a_{j}}(2\beta _{j}+\sigma _{j}^{2})\right. \\&\left. +\,\frac{1}{2\kappa }\sigma _{j}^{2}-\frac{a_j}{ \kappa + a_{j}}\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}\left( a_k-a_j\right) + C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}\left( a_k-a_j\right) \right) ,\nonumber \\ \end{aligned}$$

(14)

where $C_{j}=A_{j}(1)$ is defined in (11). Since the generator matrix $\Theta$ is irreducible, then for $C=(C_1,\ldots ,C_m)^T$, there exists $\Lambda =(a_1,\ldots ,a_m)^T$ solution of the Poisson system [21]

$$\begin{aligned} \Theta \Lambda =-C+\left( \sum _{j=1}^m\pi _jC_j\right) \mathbf {e}, \end{aligned}$$

(15)

where $\mathbf {e}$ denotes the column vector with all its entries equal to 1. Inject (15) in (14), we obtain

$$\begin{aligned} \nonumber \mathcal {L}V_{1}\le & {} -2\omega _{1}\mu _{j}(1-S)^2 -2\omega _{2}(\mu _{j}+\gamma _{j})R^{2} +\frac{1}{\kappa }(\kappa + a_{j})I^{\frac{1}{\kappa }}\left( \frac{\kappa \omega _{1}}{\kappa + a_{j}}(2\beta _{j}+\sigma _{j}^{2})\right. \\&+\left. \frac{1}{2\kappa }\sigma _{j}^{2}+\frac{a_j}{ \kappa + a_{j}}\left( C_{j}-\sum _{j=1}^{m}\pi _jC_{j}\right) +\sum _{j=1}^{m}\pi _jC_{j}\right) \nonumber \\\triangleq & {} - K^{1}_j(1-S)^2 -K^{2}_{j}R^{2}-K^{3}_jI^{\frac{1}{\kappa }}. \end{aligned}$$

(16)

By (12), we can choose a sufficiently large $\kappa _{0}$ such that

$$\begin{aligned} \max _{j\in \mathbb {S}}\left\{ \frac{1}{2\kappa _{0}}\sigma _{j}^{2}+\frac{a_j}{ \kappa _{0}+ a_{j}}\left( C_{j}-\sum _{j=1}^{m}\pi _jC_{j}\right) +\sum _{j=1}^{m}\pi _jC_{j}\right\} <0. \end{aligned}$$

Let us then choose $\kappa$ and $\omega _{1}$ such that $\kappa >\max \{-\min _{j\in \mathbb {S}}\{ a_{j}\},\kappa _{0},1\},$ and

$$\begin{aligned} 0<\omega _{1}< & {} -\frac{\kappa + \min _{j\in \mathbb {S}}\{a_{j}\}}{\kappa \left( 2\max _{j\in \mathbb {S}}\{\beta _{j}\}+ \max _{j\in \mathbb {S}}\{\sigma _{j}^{2}\}\right) }\\&\times \max _{j\in \mathbb {S}}\left\{ \frac{1}{2\kappa }\sigma _{j}^{2}+\frac{a_j}{ \kappa + a_{j}}\left( C_{j}-\sum _{j=1}^{m}\pi _jC_{j}\right) +\sum _{j=1}^{m}\pi _jC_{j}\right\} , \end{aligned}$$

which means that the coefficients of $(1-S)^{2}, I^{2}$ and $R^{2}$ in (16) are all negatives. According to Lemma 2.1 the proof is completed. $\square$

3 Almost sure exponential stability

Theorem 3.1

For any initial values $(S_{0},I_{0}, R_{0})\in \Delta$, the solution of the stochastic differential equation (6) obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\log \left( 1-S(t)+I(t)+R(t)\right) \le \sum _{j=1}^{m}\pi _j\left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) \,\,\,\,\,a.s., \end{aligned}$$

(17)

Moreover, if

$$\begin{aligned} \sum _{j=1}^{m}\pi _j\left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) <0, \end{aligned}$$

then the disease-free $E_{0}$ is almost surely exponentially stable in $\Delta$. In other words, the disease dies out with probability one.

Proof

Let us define the functions $V_{2}(S,I,R,j)=\log \left( 1-S+I+R\right) .$ By the Itô’s formula, we have

$$\begin{aligned} dV_{2}= & {} \frac{1}{1-S+I+R}\left( -\mu _{r}(1-S)+2\beta _{r}SI-\mu _{r}I-(\mu _{r}+2\gamma _{r})R\right) dt\\&-\,2\sigma _{r}^{2} \left( \frac{SI}{1-S+I+R}\right) ^{2}dt+ \frac{2\sigma _{r}SI}{1-S+I+R}dB. \end{aligned}$$

Since

$$\begin{aligned} \frac{1}{1-S+I+R}\left( -\mu _{r}(1-S)-\mu _{r}I-(\mu _{r}+2\gamma _{r})R\right) \le -\mu _{r}, \end{aligned}$$

we can easily obtain

$$\begin{aligned} \nonumber dV_{2} \nonumber\le & {} \left( -2\sigma _{r}^{2}\left( \frac{SI}{1-S+I+R} -\frac{\beta _{r}}{2\sigma _{r}^{2}}\right) ^{2}+\frac{\beta _{r}^{2}-2\mu _{r}\sigma _{r}^{2}}{2\sigma _{r}^{2}}\right) dt+ \frac{2\sigma _{r}SI}{1-S+I+R}dB\\ \nonumber\le & {} \left( \frac{\beta _{r}^{2}-2\mu _{r}\sigma _{r}^{2}}{2\sigma _{r}^{2}}\right) dt+ \frac{2\sigma _{r}SI}{1-S+I+R}dB . \end{aligned}$$

By integration, we get

$$\begin{aligned} V_{2}(t)\le V_{2}(0)+\int _{0}^{t}\left( \frac{\beta _{r(s)}^{2}-2\mu _{r(s)}\sigma _{r(s)}^{2}}{2\sigma _{r(s)}^{2}} \right) ds+M_{t}, \end{aligned}$$

(18)

where

$$\begin{aligned} M_{t}=\int _{0}^{t}\frac{2\sigma _{r}S(s)I(s)}{1-S(s)+I(s)+R(s)}dB(s). \end{aligned}$$

We can easily show that the quadratic variation of $M_{t}$ satisfies

$$\begin{aligned}{}[M_{t},M_{t}]=\int _{0}^{t}\left( \frac{2\sigma _{r}S(s)I(s)}{1-S(s)+I(s)+R(s)}\right) ^{2}ds\le 4(\max _{j\in \mathbb {S}}\sigma _{j}^{2})t. \end{aligned}$$

Thus, by the large number theorem for martingales (see Mao [23]), we have

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{M_t}{t}=0\,\,\,\,\,a.s, \end{aligned}$$

(19)

and by the ergodic theory of the Markov chain

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\int _{0}^{t}\left( \frac{\beta _{r(s)}^{2}-2\mu _{r(s)}\sigma _{r(s)}^{2}}{2\sigma _{r(s)}^{2}} \right) ds=\sum _{j=1}^{m}\pi _j\left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) \,\,\,\,\,a.s. \end{aligned}$$

(20)

From (18), (19) and (20) we obtain the desired asseration. $\square$

4 Moment exponential stability

Now, we present the following theorem which gives conditions for the moment exponential stability of the free-disease equilibrium state of the stochastic model (6).

Theorem 4.1

For any initial values $(S_{0},I_{0}, R_{0})\in \Delta$ and $p>0$, the solution of the stochastic differential equation (6) obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\log \mathbb {E}\left[ (1-S(t)+I(t)+R(t))^p\right] \le p\sum _{j=1}^{m}\pi _j\left( \left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +2p\sigma _j^2\right) .\nonumber \\ \end{aligned}$$

(21)

Moreover, if

$$\begin{aligned} \sum _{j=1}^{m}\pi _j\left( \left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +2p\sigma _j^2\right) <0, \end{aligned}$$

then the free-disease equilibrium state $E_{0}$ is pth moment exponentially stable in $\Delta$.

Proof

Let $p>0$. From (18), we have

$$\begin{aligned} \nonumber \log ((1-S(t)+I(t)+R(t))^p)\le & {} \log ((1-S_0+I_0+R_0)^p)+ pM_t\\&+p\int _{0}^{t}\left( \frac{\beta _{r(s)}^{2}-2\mu _{r(s)}\sigma _{r(s)}^{2}}{2\sigma _{r(s)}^{2}} \right) ds. \end{aligned}$$

(22)

By the ergodic theory of Markov chain, we have, for all $\varepsilon >0$ and for all t sufficiently large

$$\begin{aligned} \int _{0}^{t}\left( \frac{\beta _{r(s)}^{2}-2\mu _{r(s)}\sigma _{r(s)}^{2}}{2\sigma _{r(s)}^{2}} \right) ds\le \left( \sum _{j=1}^{m}\pi _j\left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +\frac{\varepsilon }{2p}\right) t. \end{aligned}$$

(23)

Combining (22) and (23) and taking expectation yields

$$\begin{aligned} \mathbb {E}\left( \frac{(1-S(t)+I(t)+R(t))^p}{(1-S_0+I_0+R_0)^p}\right) \le e^{p\left( \sum _{j=1}^{m}\pi _j\left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +\frac{\varepsilon }{2p}\right) t}\times \mathbb {E}e^{pM_t}, \end{aligned}$$

(24)

where $pM_t$ is a real-valued continuous martingale, with $pM_0=0$, having the quadratic variation

$$\begin{aligned}{}[pM_t]=p^2\int _{0}^{t}\left( \frac{2\sigma _{r}S(s)I(s)}{1-S(s)+I(s)+R(s)}\right) ^{2}ds\le 4p^2\int _{0}^{t}\sigma _{r(s)}^2ds, \end{aligned}$$

which implies, by using the ergodic propriety of r(t),

$$\begin{aligned}{}[pM_t]\le p^2 \left( \sum _{j=1}^{m}4\pi _j\sigma _j^2+\frac{\varepsilon }{p^{2}}\right) t, \quad \text{ for } \text{ large } \text{ t }. \end{aligned}$$

Hence, the associated exponential of $pM_t$, that is $e^{pM_t-\frac{1}{2}[pM_t]}$, is martingale. So, for t sufficiently large, we have

$$\begin{aligned} \mathbb {E}\left( e^{pM_t}\right) = \mathbb {E}\left( e^{\frac{1}{2}[pM_t]}\right) \le e^{\frac{1}{2}p^2\left( \sum _{j=1}^{m}4\pi _j\sigma _j^2+\frac{\varepsilon }{p^{2}}\right) t}. \end{aligned}$$

(25)

Combining (24) and (25) yields

$$\begin{aligned} \mathbb {E}\left( \frac{(1-S(t)+I(t)+R(t))^p}{(1-S_0+I_0+R_0)^p}\right) \le e^{p\sum _{j=1}^{m}\left( \pi _j\left( \left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +2p\sigma _j^2\right) +\frac{\varepsilon }{p}\right) t}. \end{aligned}$$

Then

$$\begin{aligned}&\limsup _{t\rightarrow \infty } \frac{1}{t}\log \mathbb {E}\left[ (1-S(t)+I(t)+R(t))^p\right] \\&\quad \le p\sum _{j=1}^{m}\pi _j\left( \left( \frac{\beta _{j}^{2}-2\mu _{j}\sigma _{j}^{2}}{2\sigma _{j}^{2}}\right) +2p\sigma _j^2\right) +\varepsilon . \end{aligned}$$

By letting $\varepsilon \rightarrow 0$, we obtain the desired results. $\square$

5 Persistence of the disease

Firstly, let us begin with the following proposition which will be useful in our study of the persistence of SDE model (6).

Proposition 5.1

Let X and Y be two positive processus with initial values $X_{0}$ and $Y_{0}$ and satisfying the differential equation

$$\begin{aligned} dX(t)=\left( -a_{r(t)}X(t)+b_{r(t)}Y(t)\right) dt, \quad \text{ for } \text{ all } \quad t>0, \end{aligned}$$

(26)

where $a_{j}>0$ and $b_{j}>0$ are positives constants for all $j\in \mathbb {S}.$ Then, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }X(t)\le \frac{\max _{j\in \mathbb {S}}b_{j}}{\min _{j\in \mathbb {S}}a_{j}} \limsup _{t\rightarrow \infty }Y(t), \end{aligned}$$

(27)

$$\begin{aligned} \liminf _{t\rightarrow \infty }Y(t)\le \frac{\max _{j\in \mathbb {S}}a_{j}}{\min _{j\in \mathbb {S}}b_{j}} \liminf _{t\rightarrow \infty }X(t). \end{aligned}$$

(28)

Proof

Let $\varepsilon >0$ be sufficiently small. Then there exists $t_{0}$ such that for all $t\ge t_{0}$,

$$\begin{aligned} Y(t)\le \limsup _{t\rightarrow \infty }Y(t)+\varepsilon . \end{aligned}$$

(29)

From (26), we have

$$\begin{aligned} dX(t)+(\min _{j\in \mathbb {S}}a_{j})X(t)dt\le (\max _{j\in \mathbb {S}}b_{j})Y(t)dt. \end{aligned}$$

By integration, we get

$$\begin{aligned} X(t)\le & {} (\max _{j\in \mathbb {S}}b_{j})\int _{t_{0}}^{t}Y(s)e^{(\min _{j\in \mathbb {S}}a_{j})(s-t)}ds+X(t_{0})e^{(\min _{j\in \mathbb {S}}a_{j})(t_{0}-t)}. \end{aligned}$$

(30)

From (29) and (30), we obtain

$$\begin{aligned} X(t)\le & {} \frac{\max _{j\in \mathbb {S}}b_{j}}{\min _{j\in \mathbb {S}}a_{j}}\left( \limsup _{t\rightarrow \infty }Y(t)+\varepsilon \right) \left( 1-e^{(\min _{j\in \mathbb {S}}a_{j})(t_{0}-t)}\right) \nonumber \\&+X(t_{0})e^{(\min _{j\in \mathbb {S}}a_{j})(t_{0}-t)}. \end{aligned}$$

(31)

By letting $t\rightarrow \infty$ and $\varepsilon \rightarrow 0$, we get the required assertion (27).

Similarly, from (26) we have for all sufficiently small $\varepsilon >0$, there exists $t_{0}'$ such that for all $t\ge t_{0}'$,

$$\begin{aligned} X(t)\ge & {} \frac{\min _{j\in \mathbb {S}}b_{j}}{\max _{j\in \mathbb {S}}a_{j}}\left( \liminf _{t\rightarrow \infty }Y(t)-\varepsilon \right) \left( 1-e^{(\max _{j\in \mathbb {S}}a_{j})(t_{0}'-t)}\right) \nonumber \\&+X(t_{0})e^{(\max _{j\in \mathbb {S}}a_{j})(t_{0}'-t)}, \end{aligned}$$

(32)

and by letting $t\rightarrow \infty$ and $\varepsilon \rightarrow 0$, we obtain th desired assertion (28). $\square$

Thereafter, we shall establish the persistence of disease under different conditions on the intensities of noises and the parameters of the model. To begin with, let us define the two sets $J_{\ge }=\{j\in \mathbb {S}, \beta _{j}\ge \sigma ^{2}_{j}\}$, $J_{<}=\{j\in \mathbb {S}, \beta _{j}<\sigma ^{2}_{j}\},$ and recall the following functions which will be used extensively in what follows,

$$\begin{aligned} A_j(x)=-\frac{1}{2}\sigma _{j}^{2}x^{2}+\beta _j x-(\mu _{j}+\alpha _{j}),\,\,\, \text{ for } \text{ all }\,x\in (0,1)\, \text{ and } \, j\in \mathbb {S}. \end{aligned}$$

(33)

Theorem 5.1

For any initial values $(S_{0},I_{0}, R_{0})\in \Delta$, if for any $j\in J_{<}$

$$\begin{aligned} C_{j}>0 \,\,\text{ and } \,\,\sum _{j\in J_{\ge }} \pi _{j}C_{j}>0, \end{aligned}$$

(34)

where the quantities $C_{j}$ are defined in (11), then the solution of SDE (6) obeys

• (a) $\limsup _{t\rightarrow \infty }S(t)\ge \nu _{1}$, a.s.,

• (b) $\liminf _{t\rightarrow \infty }S(t)\le \nu _{2}$, a.s,

• (c) $\limsup _{t\rightarrow \infty }I(t)\ge \frac{\min _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})}{\min _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})+\max _{j\in \mathbb {S}}\lambda _{j}} (1-\nu _{2})$, a.s.,

• (d) $\liminf _{t\rightarrow \infty }I(t)\le \frac{\max _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})}{\max _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})+\min _{j\in \mathbb {S}}\lambda _{j}} (1-\nu _{1})$ , a.s.,

• (e) $\limsup _{t\rightarrow \infty }R(t)\ge \frac{\min _{j\in \mathbb {S}}\lambda _{j}}{\max _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})+\min _{j\in \mathbb {S}}\lambda _{j}} (1-\nu _{2})$, a.s.,

• (f) $\liminf _{t\rightarrow \infty }R(t)\le \frac{\max _{j\in \mathbb {S}}\lambda _{j}}{\min _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})+\max _{j\in \mathbb {S}}\lambda _{j}} (1-\nu _{1})$ , a.s.,

where, for $j\in J_{<}$, $\xi _{j}$ and $\xi$ are, respectively the unique positives roots, on (0, 1), of

$$\begin{aligned} A_{j}(x)=0 \,\,\,\text{ and }\,\,\,\sum _{j\in J_{\ge }} \pi _{j}A_{j}(x)=0, \end{aligned}$$

and $\nu _{1}=\min \left\{ \xi ,\min _{j\in J_{<}}\{\xi _{j}\}\right\}$ and $\nu _{2}=\max \left\{ \xi ,\max _{j\in J_{<}}\{\xi _{j}\}\right\}$.

Proof

(a) By the Itô’s formula, we get from (6)

$$\begin{aligned} \log (I(t))=\log (I(0))+\int _{0}^{t}A_{r(s)}(S(s))ds+ \int _{0}^{t}\sigma _{r(s)}S(s)dB(s). \end{aligned}$$

(35)

From (34), we have for any $j\in J_{<}$,

$$\begin{aligned} A_j(0)=-(\mu _{j}+\alpha _{j})<0 \quad \text{ and }\quad A_j(1)=C_{j}>0. \end{aligned}$$

(36)

Then, for any $j\in J_{<}$, the equation $A_j(x)=0$ admits a unique root $\xi _j\in (0,1)$. Moreover $A_j(x)$ is increasing on $(0,\xi _j)$ and for all sufficiently small $\varepsilon >0$, for any $j\in J_{<}$ and all x such that $0<x\le \xi _{j}-\varepsilon$, we have

$$\begin{aligned} A_j(x)\le A_j(\xi _j-\varepsilon )<0. \end{aligned}$$

(37)

Similarly, by (34), the equation $\sum _{j\in J_{\ge }}\pi _j A_j(x)=0$ admits a unique root $\xi \in (0,1)$. So, one can easily show that, for all sufficiently small $\varepsilon >0$, and x such that $0<x\le \xi -\varepsilon$, we have

$$\begin{aligned} \sum _{j\in J_{\ge }}\pi _jA_j(x)\le \sum _{j\in J_{\ge }}\pi _jA_j(\xi -\varepsilon )<0. \end{aligned}$$

(38)

We now begin to prove assertion (a). If it is not true, then there is a sufficiently small $\varepsilon >0$ such that

$$\begin{aligned} \mathbb {P}\left( \limsup _{t\rightarrow \infty }S(t)\le \min \left\{ \xi ,\min _{j\in J_{<}}\{\xi _{j}\}\right\} -2\varepsilon \right) >0. \end{aligned}$$

Let us put

$$\begin{aligned} \Omega _{1}=\left\{ \limsup _{t\rightarrow \infty }S(t)\le \min \left\{ \xi ,\min _{j\in J_{<}}\{\xi _{j}\}\right\} -2\varepsilon \right\} . \end{aligned}$$

(39)

Hence, for every $\omega \in \Omega _{1}$, there is a $T(\omega )>0$ such that

$$\begin{aligned} S(t)\le \min \left\{ \xi ,\min _{j\in J_{<}}\{\xi _{j}\}\right\} -\varepsilon <1\,\,\,\,\,\, \,\,\forall \,\, t\ge T(\omega ), \end{aligned}$$

(40)

which means, for any $s\ge T(\omega )$ such that $r(s)\in J_{<}$, we have

$$\begin{aligned} 0\le S(s)\le \xi _{r(s)}-\varepsilon . \end{aligned}$$

(41)

Form (37) and (41) we have, for any $s\ge T(\omega )$ such that $r(s)\in J_{<}$

$$\begin{aligned} A_{r(s)}(S(s))\le A_{r(s)}(\xi _{r(s)}-\varepsilon )<0. \end{aligned}$$

(42)

On the other hand, for any $j\in J_{\ge }$, the function $A_j$ is increasing on (0, 1). This implies, by (40), that

$$\begin{aligned} A_{r(s)}(S(s))\le A_{r(s)}(\xi -\varepsilon ) \,\,\,\,\,\, \,\,\forall \,\, s\ge T(\omega ),\,\,\,r(s)\in J_{\ge }. \end{aligned}$$

(43)

Moreover, by the large number theorem for martingales, there is a $\Omega _{2}\subset \Omega$ with $\mathbb {P}(\Omega _{2})=1$ such that for every $\omega \in \Omega _{2}$,

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t}\int _{0}^{t}\sigma _{r(s)}S(s)dB(s)=0. \end{aligned}$$

(44)

Now, fix any $\omega \in \Omega _{1}\cap \Omega _{2}$. It then follows from (35), (42) and (43) that, for $t\ge T(\omega )$

$$\begin{aligned} \log (I(t))\le & {} \log (I(0))+ \int _{0}^{T(\omega )}A_{r(s)}(S(s))ds+ \int _{T(\omega )}^{t}1_{\{r(s)\in J_{\ge }\}}A_{r(s)}(\xi -\varepsilon )ds\nonumber \\&+ \int _{T(\omega )}^{t}1_{\{r(s)\in J_{<}\}}A_{r(s)}(\xi _{r(s)}-\varepsilon )ds+ \int _{0}^{t}\sigma _{r(s)}S(s)dB(s). \end{aligned}$$

(45)

By the ergodic theory of the Markov chain, we have,

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\int _{T(\omega )}^{t}1_{\{r(s)\in J_{\ge }\}} A_{r(s)}(\xi -\varepsilon )ds=\sum _{j\in J_{\ge }}\pi _{j}A_{j}(\xi -\varepsilon ), \end{aligned}$$

(46)

and

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\int _{T(\omega )}^{t}1_{\{r(s)\in J_{<}\}} A_{r(s)}(\xi _{r(s)}-\varepsilon )ds=\sum _{j\in J_{<}}\pi _{j}A_{j}(\xi _{j}-\varepsilon ). \end{aligned}$$

(47)

From (37), (38), (44), (45), (46) and (47), we get

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\log (I(t))\le \sum _{j\in J_{\ge }}\pi _{j}A_{j}(\xi -\varepsilon )+ \sum _{j\in J_{<}}\pi _{j}A_{j}(\xi _{j}-\varepsilon ) <0. \end{aligned}$$

(48)

Whence $\lim _{t\rightarrow \infty } I(t)=0$. On the other hand, form the third equation of (6) and (27), wa have

$$\begin{aligned} \limsup _{t\rightarrow \infty }R(t)\le \frac{\max _{j\in \mathbb {S}}\lambda _{j}}{\min _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})} \limsup _{t\rightarrow \infty }I(t). \end{aligned}$$

(49)

Hence, $\lim _{t\rightarrow \infty } R(t)=0$ and then $\lim _{t\rightarrow \infty }S(t)=1$. But this contradicts (40). The required assertion (a) must therefore hold.

(b) Similarly, if it were not true, we can then find an $\varepsilon '>0$ sufficiently small such that $\mathbb {P}\left( \Omega _{3}\right) >0,$ where

$$\begin{aligned} \Omega _{3}=\left\{ \liminf _{t\rightarrow \infty }S(t)\ge \max \left\{ \xi ,\max _{j\in J_{<}}\{\xi _{j}\}\right\} +2\varepsilon '\right\} . \end{aligned}$$

Hence, for every $\omega \in \Omega _{3}$, there is a $T'(\omega )>0$ such that

$$\begin{aligned} S(t)\ge \max \left\{ \xi ,\max _{j\in J_{<}}\{\xi _{j}\}\right\} +\varepsilon ' \,\,\,\,\,\, \,\,\forall \,\, t\ge T'(\omega ), \end{aligned}$$

(50)

As in (42) and (43), we can easily check, by choosing $\varepsilon '>0$ sufficiently small that

$$\begin{aligned}&A_{r(s)}(S(s))\ge A_{r(s)}(\xi _{r(s)}+\varepsilon ')>0 \,\,\,\,\,\,\,\,\forall \,\, s\ge T'(\omega ),\,\,\,r(s)\in J_{<}, \end{aligned}$$

(51)

$$\begin{aligned}&\sum _{j\in J_{\ge }}\pi _{j}A_{j}(\xi +\varepsilon ')>0\,\,\,\,\text{ and }\quad A_{r(s)}(S(s))\ge A_{r(s)}(\xi +\varepsilon ')\,\,\,\,\,\,\,\, \forall \,\, s\ge T'(\omega ),\,\,\,r(s)\in J_{\ge }.\nonumber \\ \end{aligned}$$

(52)

By (51), (52) and similarly to (48), we obtain

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} \log (I(t))\ge \sum _{j\in J_{\ge }}\pi _{j}A_{j}(\xi +\varepsilon ')+ \sum _{j\in J_{<}}\pi _{j}A_{j}(\xi _{j}+\varepsilon ')>0. \end{aligned}$$

Whence $\lim _{t\rightarrow \infty } I(t)=\infty .$ This contradicts $I(t)<1$. The proof of (b) is completed.

(d) By (a) and the fact that $I+R=1-S$, we have

$$\begin{aligned} \liminf _{t\rightarrow \infty }I(t)+\liminf _{t\rightarrow \infty }R(t)\le 1-\min \left\{ \xi ,\min _{j\in J_{<}}\{\xi _{j}\}\right\} ,\,\,\,\,\,a.s. \end{aligned}$$

(53)

By the third equation of (6) and (28), wa have

$$\begin{aligned} \liminf _{t\rightarrow \infty }I(t)\le \frac{\max _{j\in \mathbb {S}}(\mu _{j}+\gamma _{j})}{\min _{j\in \mathbb {S}}\lambda _{j}} \liminf _{t\rightarrow \infty }R(t). \end{aligned}$$

(54)

Combining (53) and (54) we get the required assertion (d).

(c) Similarly to (d) , it follows easily by (27), (b) and $I+R=1-S$.

(e)–(f) they follow immediately from $R=1-S-I$, (a), (b), (c) and (d). $\square$

Now, we make Theorem 5.1 more explicit in the tow following special cases.

Corollary 5.1

If for any $j\in \mathbb {S}$,

$$\begin{aligned} \beta _{j}\ge \sigma ^{2}_{j}\, \text{ and } \,\sum _{j\in \mathbb {S}}\pi _{j}C_{j}>0, \end{aligned}$$

then the estimates (a)–(f) of Theorem 5.1 hold with $\nu _{1}=\nu _{2}=\xi$. Else if for any $j\in \mathbb {S}$,

$$\begin{aligned} \beta _{j}< \sigma ^{2}_{j} \, \text{ and } \, C_{j}>0, \end{aligned}$$

then (a)–(f) hold with $\nu _{1}=\min _{j\in \mathbb {S}}\{\xi _{j}\}$ and $\nu _{2}=\max _{j\in \mathbb {S}}\{\xi _{j}\}$.

6 Positive recurrence

In this section, we show the persistence of the disease in the population, but from another point of view. Precisely, we find a domain $\mathcal {D }\subset \mathbb {R}^2_+$ which is positive recurrent for the process (S(t), I(t)). Generally, the process $X^x_t$ where $X_0=x$ is recurrent with respect to $\mathcal {D}$ if, for any $x\notin \mathcal {D}$, $\mathbb {P}\left( \tau _{D}<\infty \right) =1$, where $\tau _{D}$ is the hitting time of $\mathcal {D}$ for the process $X^x_t$, that is

$$\begin{aligned} \tau _{D}=\inf \left\{ t>0, X^x_t\in \mathcal {D}\right\} . \end{aligned}$$

The process $X^x_t$ is said to be positive recurrent with respect to $\mathcal {D}$ if $\mathbb {E}(\tau _{D})<\infty$, for any $x\notin \mathcal {D}$.

Theorem 6.1

Consider the stochastic system (6) with initial condition in $\Delta$. Assume that

$$\begin{aligned} \sum _{j=1}^m\pi _jC_j>0, \end{aligned}$$

(55)

then there exists $\alpha >0$ such that (S(t), I(t)) is positive recurrent with respect to the domain

$$\begin{aligned} \mathcal {D}=\left\{ x\in \mathbb {R}^2_+; x_{1}+x_{2}\le 1, \frac{1}{\alpha }<x_{1}<1-\frac{1}{\alpha }, \frac{1}{\alpha }<x_{2}<1-\frac{1}{\alpha }\right\} . \end{aligned}$$

Proof

Consider the positive functions defined on $(0,1)^{2}\times \mathbb {S}$ by

$$\begin{aligned} \psi ((x_{1},x_{2}),j)= & {} \left( \frac{1}{\eta }+\varpi _j\right) x_{1}^{-1} x_{2}^{-\eta }. \end{aligned}$$

Here, $\eta$ is a positive number sufficiently small satisfying $\frac{1}{\eta }>-\underset{j\in \mathcal {S}}{\min }\varpi _j$, where $\varpi =(\varpi _1,\ldots ,\varpi _m)^T$ will be determined in the rest of the proof. The differential operator $\mathcal {L}$ acting on the Lyapunov function $\psi$ gives

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)= & {} -\eta \left( \frac{1}{\eta }+\varpi _j\right) S^{-1}I^{-\eta -1 }\left( -(\mu _j+\lambda _j)I+\beta _jSI\right) \nonumber \\&+\,\frac{1}{2}\eta (1+\eta )\left( \frac{1}{\eta }+\varpi _j\right) \sigma _j^2SI^{-\eta }+ S^{-1}I^{-\eta }\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)\nonumber \\&-\,\left( \frac{1}{\eta }+\varpi _j\right) I^{-\eta }S^{-2}\left( \mu _j-\mu _jS-\beta _j SI +\gamma _jR\right) \nonumber \\&+\,\sigma _{j}^{2}\left( \frac{1}{\eta }+\varpi _j\right) I^{-\eta +2 }S^{-1} +\eta \left( \frac{1}{\eta }+\varpi _j\right) \sigma _j^2I^{-\eta +1 } \nonumber \\= & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ \frac{1}{1+\eta \varpi _j} \sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)\right. \nonumber \\&+\,\frac{1}{2}(1+\eta )\sigma _j^2S^2+\mu _j+\lambda _j-\beta _jS \nonumber \\&+\,\sigma _j^2SI -\left. \frac{S^{-1}}{\eta }\left( \mu _j-\mu _jS-\beta _j SI +\gamma _jR-\sigma _{j}^{2}SI^{2}\right) \right] . \end{aligned}$$

(56)

Using $S=1-I-R$, we get, from (56),

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)= & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ \mu _j+\lambda _j-\beta _j +\frac{1}{2} \sigma _j^2 +\frac{1}{2}\eta \sigma _j^2+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\right. \nonumber \\&\left. -\,\frac{\eta \varpi _j}{1+\eta \varpi _j}\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+ \beta _j I+\beta _j R +\sigma _j^2SI\right. \nonumber \\&-\left. \frac{S^{-1}}{\eta }\left( \mu _j-\mu _jS-\beta _j SI +\gamma _jR-\sigma _{j}^{2}SI^{2}\right) \right] \nonumber \\= & {} \,\,\left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\beta _j I+\beta _j R+\sigma _{j}^{2}SI \right. \nonumber \\&+\left. \frac{S^{-1}}{\eta }\left( -\mu _j+\mu _jS+\beta _j SI -\gamma _jR+\sigma _{j}^{2}SI^{2}\right) +\mathcal {O}(\eta )\right] . \end{aligned}$$

(57)

Let $S,I\in \mathcal {D}^c$, which implies by $S+I<1$ that either $S<\frac{1}{\alpha }$ or $I<\frac{1}{\alpha }$. Firstly, if $S<\frac{1}{\alpha }$ then from $I,\,R,\, I+R\in (0,1)$ and (57), we have

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)\le & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\beta _j +\sigma _{j}^{2} \right. \nonumber \\&+\left. \frac{S^{-1}}{\eta }\left( -\mu _j+\frac{\mu _j+\beta _j+\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}(\eta )\right] , \end{aligned}$$

therefore, for all $\alpha > \max _{j\in \mathbb { S}}\left\{ \frac{\mu _j+\beta _j+\sigma _{j}^{2}}{\mu _j}\right\}$ and $\eta$ sufficiently small, we have

$$\begin{aligned} \nonumber \mathcal {L}\psi ((S,I),j)\le & {} \left( 1+\eta \varpi _j\right) \alpha \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\beta _j +\sigma _{j}^{2} \right. \nonumber \\&+\left. \frac{\alpha }{\eta }\left( -\mu _j+\frac{\mu _j+\beta _j+\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}(\eta )\right] \le -1. \end{aligned}$$

(58)

Secondly, if $I<\frac{1}{\alpha }$, then, from $-\mu _j+\mu _jS<0$ and (57), we have

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)\le & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\beta _j I+\beta _j R+\sigma _{j}^{2}SI \right. \nonumber \\&+\left. \frac{S^{-1}}{\eta }\left( \beta _j SI -\gamma _jR+\sigma _{j}^{2}SI^{2}\right) +\mathcal {O}(\eta )\right] \\\le & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)+\frac{\beta _j}{\alpha }+\frac{\sigma _{j}^{2}}{\alpha } \right. \\&\left. +\,R\left( \beta _j-\frac{\gamma _j}{\eta }\right) + \frac{1}{\alpha \eta }\left( \beta _j+\frac{\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}(\eta )\right] . \end{aligned}$$

For $\eta$ sufficiently small such that $\frac{1}{\eta }>\max _{j\in \mathbb {S}}\frac{\beta _j}{\gamma _j }$, we have

$$\left( \beta _j-\frac{\gamma _j}{\eta }\right) <0, \,\,\,\text{ for } \text{ all }\,\, j\in \mathbb {S},$$

then

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)\le & {} \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -C_{j}+\sum _{k\ne j, k\in \mathbb { S}}\theta _{jk}(\varpi _k-\varpi _j)\nonumber \right. \\&\left. + \,\frac{1}{\alpha \eta }\left( \beta _j+\frac{\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}\left( \frac{1}{\alpha }\right) +\mathcal {O}(\eta )\right] . \end{aligned}$$

(59)

On the other hand, the generator matrix $\Theta$ is irreducible, then for $C=(C_1,\ldots ,C_m)^T$ there exists $\varpi ^T=(\varpi _1,\ldots ,\varpi _m)^T$ solution of the Poisson system [21]

$$\begin{aligned} \Theta \varpi =C-\left( \sum _{j=1}^m\pi _jC_j\right) \mathbf {e}, \end{aligned}$$

(60)

where $\mathbf {e}$ denotes the column vector with all its entries equal to 1. Substituting (60) in (59) yields

$$\begin{aligned}&\mathcal {L}\psi ((S,I),j)\nonumber \\&\quad \le \left( 1+\eta \varpi _j\right) S^{-1}I^{-\eta } \left[ -\sum _{j=1}^m\pi _jC_j+\frac{1}{\alpha \eta }\left( \beta _j+\frac{\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}\left( \frac{1}{\alpha }\right) +\mathcal {O}(\eta )\right] .\nonumber \\ \end{aligned}$$

(61)

One can easily verify that for $\eta$ sufficiently small there exists $\alpha _{0}=\alpha _{0}(\eta ,\varpi _1,\ldots ,\varpi _m)$ such that for all $\alpha >\alpha _{0}$ we have

$$\begin{aligned} -\sum _{j=1}^m\pi _jC_j+ \frac{1}{\alpha \eta }\left( \beta _j+\frac{\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}\left( \frac{1}{\alpha }\right) +\mathcal {O}(\eta )<0, \end{aligned}$$

(62)

which is allowed by the condition (55). Combining (61) and (62), we obtain in the case when $I<\frac{1}{\alpha }$ such that $\eta$ sufficiently small and $\alpha >\alpha _{0}$

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)\le & {} \left( 1+\eta \varpi _j\right) \alpha ^{\eta } \left[ -\sum _{j=1}^m\pi _jC_j + \frac{1}{\alpha \eta }\left( \beta _j+\frac{\sigma _{j}^{2}}{\alpha }\right) +\mathcal {O}\left( \frac{1}{\alpha }\right) +\mathcal {O}(\eta )\right] \nonumber \\\le & {} -1. \end{aligned}$$

(63)

From (58) and (63), we have for $\eta$ sufficiently small and $\alpha >\max \left( \alpha _{0}, \max _{j\in \mathbb { S}} \left\{ \frac{\mu _j+\beta _j+\sigma _{j}^{2}}{\mu _j}\right\} \right)$,

$$\begin{aligned} \mathcal {L}\psi ((S,I),j)\le -1,\quad \text{ for } \text{ all } ((S,I),j)\in \mathcal {D}^c\times \mathbb {S}. \end{aligned}$$

(64)

Now, Let $(S(0),I(0))\in \mathcal {D}^c$. Thanks to the generalized Itô formula established by Skorokhod [24] (Lemma 3, p.104) and using (64), we obtain

$$\begin{aligned}&\mathbb {E}\left[ \psi \left( \left( S(\tau _{\mathcal {D}}),I(\tau _{\mathcal {D}})\right) ,r(\tau _{\mathcal {D}})\right) \right] - \psi \left( \left( S(0),I(0)\right) ,r(0)\right) \\&\quad = \mathbb {E}\int ^{\tau _{\mathcal {D}}}_0\mathcal {L}\psi ((S(t),I(t)),r(t))dt \\&\quad \le \mathbb {E}(\tau _{\mathcal {D}}). \end{aligned}$$

Thus, by the positivity of $\psi$, one can deduce that

$$\begin{aligned} \mathbb {E}(\tau _{\mathcal {D}})\le \psi \left( \left( S(0),I(0)\right) ,r(0)\right) . \end{aligned}$$

The proof is complete. $\square$

7 Examples and computer simulations

Let $(r(t))_{t\ge 0}$ be a right-continuous Markov chain taking values in $\mathbb {S} = \{1, 2\}$ with the generator

$$\begin{aligned} \Theta =\begin{pmatrix} -1 &{}\quad 1 \\ 2 &{}\quad -2 \end{pmatrix}. \end{aligned}$$

Given a stepsize $\Delta >0$, the Markov chain can be simulated by Computing the one-step transition probability matrix $P=e^{\Delta \Theta }$. We refer the reader to Anderson [25] for more details. Hence for $\Delta =0.0001$, the transition probability matrix and the stationary distribution are given, respectively, by

$$\begin{aligned} P=\begin{pmatrix} 0.9999 &{}\quad 0.0001 \\ 0.0002 &{}\quad 0.9998 \end{pmatrix},\,\,\,\,(\pi _{1},\,\pi _{2})=( 0.6667,\,0.3333). \end{aligned}$$

7.1 Extinction

Example 7.1

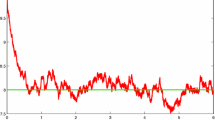
($C_{1}<0$ and $C_{2}<0$). To illustrate the extinction case of Theorem 2.2, firstly we set

$$\begin{aligned}&(\mu _{1},\mu _{2})=(0.014, 0.015 ),\,(\beta _{1},\beta _{2})=(0.3, 0.31),\,(\gamma _{1},\gamma _{2})=(0.3, 0.301),\\&\quad (\lambda _{1},\lambda _{2})=(0.4, 0.27),\, (\sigma _{1},\sigma _{2})=(0.1, 0.2). \end{aligned}$$

This implies that $\pi _{1}{C_{1}}+\pi _{2}C_{2}=0.6667\times (-0.164) + 0.3333\times (-0.075)=-0.1343<0.$ Hence, the extinction condition of Theorem 2.2 is satisfied. The computer simulations in Fig. 1, using the Euler Maruyama method (see e.g., [26]), support these results clearly.

Fig. 1

Computer simulation of a single path of $\left( S(t),I(t),R(t)\right)$ for the SDE model (6) with initial condition (0.975, 0.03, 0.02) and its corresponding Markov chain r(t) using the parameter values of Example 7.1

Example 7.2

($C_{1}<0$ and $C_{2}>0$.) Let us choose

$$\begin{aligned}&(\mu _{1},\mu _{2})=(0.014,\, 0.01401 ),\,(\beta _{1},\beta _{2})=(0.3, \, 0.301),\,(\gamma _{1},\gamma _{2})=(0.3,\, 0.302),\\&\quad (\lambda _{1},\lambda _{2})=(0.4,\, 0.09),\, (\sigma _{1},\sigma _{2})=(0.1,\, 0.2). \end{aligned}$$

This gives $\pi _{1}{C_{1}}+\pi _{2}C_{2}= 0.6667\times (-0.1640) + 0.3333\times (0.0960)= -0.0773<0.$ Then, the extinction condition of Theorem 2.2 is satisfied. The computer simulations in Fig. 2 , illustrates these results.

Fig. 2

Computer simulation of a single path of $\left( S(t),I(t),R(t)\right)$ for the SDE model (6) with initial condition (0.975, 0.03, 0.02) and its corresponding Markov chain r(t) using the parameter values of Example 7.2

7.2 Persistence

Example 7.3

($C_{1}<0$ and $C_{2}>0$). Let us choose

$$\begin{aligned}&(\mu _{1},\mu _{2})=(0.0142,\, 0.014 ),\,(\beta _{1},\beta _{2})=(0.302,\, 0.301),\,(\gamma _{1},\gamma _{2})=(0.3,\, 0.302),\\&\quad (\lambda _{1},\lambda _{2})=(0.091,\, 0.4),\, (\sigma _{1},\sigma _{2})=(0.2,\, 0.11). \end{aligned}$$

We compute $\pi _{1}{C_{1}}+\pi _{2}C_{2}=0.286>0$ and $\beta _{1}\sigma _{1}>^{2}$, $\beta _{2}\sigma _{2}>^{2}$. Hence, on one hand, the persistence condition of Corollary 5.1 is satisfied and the corresponding estimates hold with $\xi =0.7168$, that is, S(t) rises to or above the level $\xi _s=\xi =0.7168$,

$$\begin{aligned} I\in [\xi ^i_{\min }= 0.2326,\, \xi ^i_{\max }=0.0584 ] \quad \mathrm{and}\quad R \in [\xi ^r_{\min }=0.2248,\, \xi ^r_{\max } =0.0506], \end{aligned}$$

infinitely often with probability one, which is clearly illustrated by Fig. 3.

Fig. 3

Results of one simulation run of SDE (6) with initial condition (0.975, 0.03, 0.02) and its corresponding Markov chain r(t) using the parameter values of Example 7.3. Here, respectively, S(t), I(t) and R(t) rises to or above 0.7168, $[ 0.2326,\, 0.0584 ]$ and $[0.2248, \,0.0506]$ infinitely often with probability one

8 Conclusion

In this paper, we extended the classical SIRS epidemic model from a deterministic framework to a stochastic one by incorporating both white and color environmental noise. we have looked at the long-term behavior of our stochastic SIRS epidemic model. We established conditions for extinction and persistence of disease which are close to necessary. We also proved that the SIRS model (6) has a unique stationary distribution and the ergodic property.

The results show that The stationary distribution $(\pi _1,\ldots , \pi _m)$ of the Markov chain r(t) plays a very important role in determining extinction or persistence of the epidemic in the population. That is, if r(t) spends enough time in the states where $C_j$ is negative, then the epidemic die out speedily from the population. If r(t) spends many time in the states where $C_j$ is positive, then the epidemic will persists in the population if it is initially present.

We have not been able to determine the nature of the epidemic model for the case when $\sum _{j=1}^m\pi _jC_j=0$, but the computer simulation shows that the disease would die out after a long period of time, as we suspect. We have illustrated our theoretical results with computer simulations. Finally, this paper is only a first step in introducing switching regime into an epidemic model. In future investigations we plan to introduce white and color noises into more realistic epidemic models such as the SEIRS models.