Introduction

Interacting systems of structured populations are typically hard to describe. The challenges of representing hierarchical dynamics apply in multi-species ecological ensembles (Auger 1983; Coyte et al. 2015), multi-strain micro- bial pathogens (Gupta et al. 1996; Gomes and Medley 2002; Ferguson et al. 2003) and more generally across ecosystems (Levin et al. 1997). To address these challenges, models have to rely on simplification, such as aggregation methods, separation of time scales and suitable approximation (Levins 1966; Levin 1992; Adler and Brunet 1991; Auger and Poggiale 1998; De Roos et al. 2008; Rossberg and Farnsworth 2011). The study of multi-strain pathogens is growing rapidly, thanks to technological and molecular advances quantifying microbial diversity and host immunological history to unprecedented resolution (Grenfell et al. 2004; Biek et al. 2015). Yet, the principles that govern strain composition, interactions, and dynamics at the within- and between- host levels remain largely undefined.

Complex systems, such as polymorphic pathogens, typically require a high dimensional description with many degrees of freedom. Yet, their behaviour can sometimes be approximated or represented in less dimensions (Adler and Brunet 1991; Kryazhimskiy et al. 2007). The main challenge for model reduction lies in the identification of meaningful aggregated variables and projection of the effective dynamics in this low dimensional representation (Singer et al. 2009). Here, we report a new analytical framework for endemic multi-strain pathogens, characterized by direct interactions among strains upon co-infection. A resident microbial strain can decrease or increase the rate of a secondary strain acquisition for the host, and different strains might exhibit different interaction types and magnitudes (Faust and Raes 2012). How do these altered susceptibilities affect global epidemiological dynamics? We address this question focusing on a parsimonious epidemiological model that describes colonization and co-colonization dynamics by circulating subtypes of such a pathogen. We start by analyzing multi-type coexistence under symmetric interactions, and derive the explicit links with the non-symmetric system using a slow-fast dynamic decomposition, from singular perturbation theory (Tikhonov 1952; Fenichel 1979).

Our approach is inspired by Goldstone’s idea of symmetry breaking yielding slow dynamics (Goldstone et al. 1962), with applications in physics (Sethna 2006; Golubitsky 2002), and Hubell’s neutral hypothesis for community assembly processes (Hubbell 2001). A long-standing debate in ecology is whether coexistence of different species results from niche adaptation (Gause 1934), or because of a balance of neutral processes such as immigration, speciation and extinction (MacArthur 1967). This question often applies when studying genetic or antigenic polymorphisms in pathogens (Gupta and Maiden 2001; Grenfell et al. 2004; Lipsitch and O’Hagan 2007; Lipsitch et al. 2009). Most likely, neutral and niche mechanisms combine to generate coexistence patterns within and between species (Leibold et al. 2004), and one or the other may dominate depending on the scale of consideration (Adler et al. 2007; Wiegand et al. 2012). The difficulty lies in disentangling the two. In the ongoing debates on biodiversity, one way to link niche and neutral perspectives has been to address the essential role that stochasticity plays on species coexistence and community assembly processes (Chase 2003; Tilman 2004; Chisholm and Pacala 2010). Here, we follow the efforts to bridge these two macroecological theories, but we take a different path. We focus on the symmetry characteristics of pairwise interactions between biological entities and their emergent competition.

Recent studies have highlighted the shape of competition kernels as a major determinant of the equilibrium distributions of species along the phenotype space and their demographic stability (Scheffer and van Nes 2006; Leimar et al. 2013). The role of transient dynamics for species persistence on ecological timescales has also been increasingly appreciated, especially in cyclic systems (Hastings 2001). With the advent of the microbiome era (Pepper and Rosenfeld 2012; Bucci and Xavier 2014; Flint et al. 2007; Bosch et al. 2013), elucidating the dynamical components and consequences of inter- and intra-species interactions is becoming ever more important (Widder et al. 2016). Simulations of food-webs and Lotka-Volterra competitive communities have addressed the magnitude of interaction strengths (McCann et al. 1998), and the diversity of interaction types (Mougi and Kondoh 2012) for ecological community stability. Yet, analytical advances to tackle these questions across scales are still needed.

In the present study, we advocate that the slow-fast dynamics decomposition offers a useful tool to provide insight into microbial interactions. Although we analyze an endemic multi-strain pathogen and its dynamics on the epidemiological scale, our results have implications beyond this immediate system, contributing to novel conceptual unification in community ecology. We show that neutral dynamics between interacting strains occurs on a fast timescale, whereas the non-neutral stabilizing forces act on a slow timescale, dependent on trait differences manifested upon co-colonization. We quantify exactly which asymmetries matter for multi-strain coexistence, and how overall transmission intensity affects stabilization of diversity. Together, our results define a promising analytical approach to better understand microbial ecosystems.

Methods

Slow-fast systems

Separation of dynamics into fast and slow components has been invoked in numerous studies of ecological and eco-evolutionary dynamics (Rinaldi and Muratori 1992; Auger and Poggiale 1998; Rinaldi and Scheffer 2000; Hastings 2004; Cortez 2011), and more generally in the analysis of complex dynamical systems (Singer et al. 2009). The approach relies on a canonical system of equations where the variables change in two (or more) time scales, as follows:

$$\begin{array}{@{}rcl@{}} \frac{dx}{dt}&=&f(x,y) \\ \frac{dy}{dt}&=&\varepsilon g(x,y) \end{array} $$

with the small parameter 0<ε≪1, where f(x,y) and g(x,y) are bounded. In this example, y is the slow variable and x is the fast one. By taking ε=0 in this system, we obtain the critical fast system, where the slow variable may be treated as a constant: y = c o n s t. Now, assume that for any initial value x(0), x(t)→Φ(y) as \(t \to +\infty \) for some smooth function Φ satisfying f(Φ(y),y)=0 (*). The set (Φ(y),y) is called the slow manifold. When making the change of timescale τ = ε t, one obtains an equivalent slow system:

$$\begin{array}{@{}rcl@{}} \varepsilon \frac{dx}{d\tau}&=&f(x,y) \\ \frac{dy}{d\tau}&=&g(x,y) \end{array} $$
(1)

whereby taking ε=0, we obtain the critical slow dynamics. When reducing to the slow manifold x=Φ(y), this slow dynamics is defined by:

$$ \frac{d}{d\tau} z(\tau)=g({\Phi}(z),z). $$
(2)

Under the above assumption (*), the dynamics of system (1) tends to the dynamics of (2) as ε→0. The precise statement is given by Tikhonov’s theorem (Tikhonov 1952; Lobry and Sari 1998; 2005; Hoppensteadt 1966). A more geometrical point of view was obtained by Fenichel (1979) (see also (Verhulst 2007) and the references therein for a most recent overview of these methods). Identifying the slow manifold in systems with two time scales is nontrivial, the slow and fast components being often implicit functions of the original variables. Knowledge of a good parametrisation of such a slow manifold is key to the understanding and computation of complex multi-scale systems.

Multi-strain model with direct interactions at co-infection

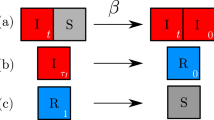
We consider a multi-type pathogen, transmitted via direct contact, following susceptible-infected-susceptible (SIS) epidemiological dynamics. Examples could include bacteria of the respiratory tract (García-Rodríguez and Martinez 2002) such as Streptococcus pneumoniae and Haemophilus influenzae, displaying several genetic and antigenic variants. In the model, we group the pathogen types in two subsets, denoted by V and N, assuming types within each group share similar features (Fig. 1). With a set of ordinary differential equations, we then track the proportion of hosts in six compartments: susceptibles, S, hosts colonized by one V type I V , hosts colonized by one N type I N , and co-colonized hosts I V V , I N N , and I V N with two types of each combination, independent of the order of their acquisition. We have:

$$ \left\{\begin{array}{ll} \frac{d}{dt} S&=\mu(1-S)-S(\lambda_V+\lambda_N)+\gamma I\\ \frac{d}{dt} I_{V}&=\lambda_V S-I_{V}(k_{VV}\lambda_V+k_{VN}\lambda_N)-(\mu+\gamma)I_{V}\\ \frac{d}{dt} I_{N}&=\lambda_N S-I_{N}(k_{NV}\lambda_V+k_{NN}\lambda_N)-(\mu+\gamma)I_{N}\\ \frac{d}{dt} I_{VV}&=k_{VV} \lambda_V I_{V}-(\mu+\gamma) I_{VV}\\ \frac{d}{dt} I_{NN}&=k_{NN} \lambda_N I_{N}-(\mu+\gamma) I_{NN}\\ \frac{d}{dt} I_{VN}&= k_{VN} \lambda_N I_{V}+k_{NV} \lambda_V I_{N}-(\mu+\gamma) I_{VN}, \end{array}\right. $$
(3)

where I = I V + I N + I V V + I N N + I V N , and the forces of infection for V and N strains are \(\lambda _V=\beta (I_{V}+I_{VV}+\frac 12 I_{VN})\) and \(\lambda _N=\beta (I_{N}+I_{NN}+\frac 12 I_{VN}). \)

Fig. 1
figure 1

Model diagram. a Pathogen subtypes grouped in two sets, V and N, characterized by within-group and between-group interaction. b SIS model structure with single and dual colonization. The black arrows refer to acquisition of a first clone with forces of infection: λ V = β(I V + I V V + I V N /2) and λ N = β(I N + I N N + I V N /2). The grey arrows refer to altered acquisition of a secondary clone k i j λ i in an already colonized host, where clone interactions can range from competition (k i j <1) to cooperation (k i j ≥1). The dashed arrows depict colonization clearance at rate γ. The white arrows reflect host demographic processes: birth and death at equal rate μ

Full size image

Because all variables refer to proportions, the last equation can be omitted using S + I=1. Susceptibles are recruited at constant rate μ, equal to the per-capita departure rate. Upon exposure, a host can become colonized by one V or N type. Single and dual carriers contribute equally to the force of infection for each group of types, and hosts carrying two pathogen clones transmit either with equal probability. β denotes the per-capita transmission rate, while γ denotes the clearance rate of any colonization episode, assuming no immune memory. Our assumption of direct clearance of co-colonization, back to the susceptible state reflects strain-transcending immunity as the main player in pathogen clearance, and is in accord with evidence from some pneumococcus studies (e.g. Malley et al. 2005). Single carriers can acquire an additional pathogen clone at a rate modified by a relative factor k i j , describing the interaction between the resident and the challenge type upon encounter. Values of k i j below 1 correspond to antagonism/competition between types from group i and j, while k i j ≥1 correspond to facilitation between clones and enhancement of host susceptibility.

Differently from an early model by Adler and Brunet (1991), also dealing with interacting strains and altered susceptibilities, we focus on strains with the same R 0 (Diekmann et al. 1990), and consider in addition interactions within strains. This structure can be traced back to a study by van Baalen and Sabelis (1995), allowing for co-infection by the same strain, which is deemed more technically correct in light of evolutionary epidemiology (Alizon and Lion 2011; Alizon 2013). In addition, we assume that two co-infecting clones share host resources, i.e. β is equal for single and dual colonization. The vulnerability factor in co-infection, detailed here by the k i j parameters, has also been modelled previously (Adler and Brunet 1991; Lipsitch et al. 2009; Alizon and Lion 2011; Alizon 2013). Thus, our formulation shares features with other co-infection models, while lending itself to analytical tractability.

We describe pathogen diversity only with a reduced number of, in this case two, groupings, assuming equivalence with respect to transmission and clearance rate. Realistic differences between pathogen types arise only in their direct interaction abilities, and are studied as symmetry-breaking perturbations to the system (Golubitsky 2002). The same model has recently been used and tested on data, in the context of competing pneumococcal capsular serotypes and vaccination effects (Gjini et al. 2016). In this new study, we go deeper in the analysis, and generalize to any form of interaction, including competition (Dawid et al. 2007) and cooperation (Xavier et al. 2011; McNally et al. 2014) between strains. These may arise from host environment modification by colonizing bacteria (Odling-Smee et al. 2003), secretion of proteins and metabolites (West et al. 2006; Nogueira et al. 2009) or immunomodulation (Brown et al. 2008), and could include the release of toxins that kill competitors (Riley and Gordon 1999), enzymes that alter the nutrient state (Dinges et al. 2000) and biofilms that protect against harsh environments (Drenkard and Ausubel 2002; Muñoz-Elías et al. 2008). By changing the local conditions in one host, these types of bacterial secretions could affect the growth of the strains producing them, but also modulate environmental features to which competitors may be relatively better or worse adapted.

In the following, we investigate the epidemiological consequences of such clone interactions, modelled through the four directed co-colonization rate modifiers (k i j ’s). We apply the slow-fast dynamics perspective to understand how minor variations in these interaction traits drive the time evolution of an endemic multi-strain system, over short and long timescales. The uncovered slow-fast dynamic decomposition directly relates to the structure of the interaction matrix, thus providing new avenues for theoretical exploration of microbial competition and facilitation networks.

Results

The rationale behind slow-fast dynamics in our model

Neutral model

The simple version of the epidemiological model uses the equivalence assumption for strain interaction at co-colonization:

$$ k_{VV}=k_{NN}= k_{VN}= k_{NV}=k. $$
(4)

We find that the neutral system always admits the trivial disease-free equilibrium, stable for \(R_{0}=\frac {\beta }{\mu +\gamma }<1\), which corresponds to a sub-critical basic reproduction number of the pathogen (Diekmann et al. 1990). In contrast, if R 0>1, the system has a full curve S 0 of neutrally-stable equilibria (see Eq. (12)), which is given by

$$\begin{array}{@{}rcl@{}} S_{0}=\left\{\left( S,I_{V}(z),I_{N}(z),I_{VV}(z),I_{NN}(z),I_{VN}(z)\right),\;z\in[-1,1]\right\}, \end{array} $$

and satisfies

$$\begin{array}{@{}rcl@{}} S&=&\frac{1}{R_{0}}, \\ I_{V}(z)+I_{N}(z)&=&I_{1}^{*} \\ I_{VV}(z)+I_{NN}(z)+I_{NV}(z)&=&I_{2}^{*}=1-S-I_{1}^{*}. \end{array} $$
(5)

More specifically,

$$I_{1}^{*}=\frac{R_{0}-1}{R_{0}(k(R_{0}-1)+1)}\text{ and }I_{2}^{*}=\frac{k(R_{0}-1)^{2}}{R_{0}(k(R_{0}-1)+1)},$$

defining a conservation law for single and dual colonization prevalence. Free variation of z∈[−1,1] fine-tunes the relative frequency distribution between types, and enables correlated hierarchies to emerge between V and N in colonization and co-colonization. If R 0>1, S 0 attracts all trajectories of the dynamical system (see Appendix B). Depending on the exact values of R 0 and k, single or dual colonization may dominate in the population. In particular if k(R 0−1)>1, co-colonization is more prevalent. Clearly, the neutral model is simple analytically, but somewhat degenerate: depending on the initial conditions, any point of S 0 may be a final attractor.

Such results stem from the symmetry constraints, related to the population-dynamic neutrality principle postulated by Hubbell (2001), in which populations can achieve equilibria at arbitrary population sizes, the requirement being a conservation law for total population size summed over all species. Here, we show analogously that in an epidemiological multi-strain system, a conservation law applies to the overall prevalence of single and dual colonization in the population, which can be freely partitioned among indistinguishable constituent strains.

The slow-fast dynamics decomposition

Our approach is to take neutrality as a first approximation, to then study the effects of deviations from it. Thus, we next consider system (3), without the neutral assumption (4), which makes it more biologically realistic, but still remains hard to analyze. We investigate the effect of differential interaction coefficients at dual colonization by two different pathogen types, thus the dynamics of (3) for

$$ k_{VV}\approx k_{NN}\approx k_{VN}\approx k_{NV}. $$
(6)

We denote by k the average within-group interaction coefficient:

$$ k =\frac{1}{2}(k_{VV}+k_{NN}). $$
(7)

Defining ε as the Euclidean distance of [k V V ,k V N ,k N V ,k N N ] from [k,k,k,k] in \(\mathbb {R}^{4}\):

$$ \epsilon=\sqrt{(k_{VV}-k)^{2}+(k_{NN}-k)^{2}+(k_{VN}-k)^{2}+(k_{NV}-k)^{2}}, $$

we can rewrite each interaction coefficient of the original system as:

$$ k_{ij}^{\varepsilon}=k+\varepsilon \alpha_{ij}, \text{ for }i,j \in\{V,N\}\text{ and \(0<\varepsilon\ll 1\)}. $$
(8)

Essentially, 𝜖 represents the deviation from neutrality in this interaction trait space between strains. By the definition of k, it follows that α V V + α N N =0. In a first approximation (ε=0), one obtains the neutral model, which we characterized above. We want to show that if ε>0 is sufficiently small, in a first time, the dynamics follow the neutral system tending quickly to some point of S 0, and in a second time, the dynamics move slowly on S 0.

Because there are two timescales which are nontrivially coupled in the system, in the following, we disentangle them by explicitly finding the fast and the slow variables. Thus, we are able to compute the slow dynamics, which are described by a single equation dependent on the coefficients α i j . By virtue of the Tikhonov theorem (Tikhonov 1952), we obtain that the long time behaviour of solutions of (3) is asymptotically close to the behavior of solutions of the slow dynamics on S 0.

Broken symmetry of strain interactions and the slow manifold

An equivalent representation by change of variables

The more detailed mathematical derivations for the dynamics for general ε ≠ 0, are given in Supporting Appendices. Here, we provide only the key for the method. The first step is to write the original system in an equivalent slow-fast form allowing the use of singular perturbation theory. For this, it is convenient to adopt the following change of variables:

$$I_{1}:=I_{V}+I_{N}, \quad I:=I_{1}+I_{VV}+I_{NN}+I_{VN} $$

and

$$J_{1}:=I_{V}-I_{N},\quad J=I_{V}-I_{N}+I_{VV}-I_{NN}. $$

With these notations, we get \(\lambda _V=\frac {\beta }{2}(I+J)\) and \(\lambda _N=\frac {\beta }{2}(I-J).\) Replacing these variables and k i j = k + ε α i j for i,j∈{N,V}, the system reads:

$$ \left\{\begin{array}{ll} \frac{d}{dt} S&=m(1-S)-\beta SI\\ \frac{d}{dt} I&=\beta S I-mI\\ \frac{d}{dt} I_{1}&=\beta SI-mI_{1}-\beta k II_{1}+\varepsilon \frac{\beta}{4}g_{0}(I,I_{1},J,J_{1})\\ \frac{d}{dt} J&=\beta S J-m J+\frac{ k\beta}{2}\left( I_{1} J-J_{1} I\right)+\varepsilon \frac{\beta}{4}g_{1}(I,I_{1},J,J_{1})\\ \frac{d}{dt} J_{1}&=\beta SJ-mJ_{1}- k\beta J_{1} I+\varepsilon \frac{\beta}{4}g_{2}(I,I_{1},J,J_{1})\\ \frac{d}{dt} I_{VN}&= -m I_{VN}+\frac{k\beta}{2}(I_{1} I-J_{1} J)+\varepsilon \frac{\beta}{4}g_{3}(I,I_{1},J,J_{1})\\ \end{array}\right. $$
(9)

where m = γ + μ and the functions g k are explicit quadratic functions of the variables I,I 1,J and J 1 and of the parameters α i j (Appendix A). The main aim for this change of variables arises from the following two facts about system (9): (i) The system is triangular by (three) blocks: the dynamics of (S,I) depend only on (S,I), the dynamics of (I 1,J,J 1) do not depend on I V N . (ii) The dynamics of the first block (S,I) do not depend on ε.

The explicit slow-fast system

The point (ii) above ensures that (S,I) tends to \((S^{*},I^{*})=\left (\frac {1}{R_{0}},1-\frac {1}{R_{0}}\right )\) as \(t\to +\infty \) and uniformly in ε. Hence, without loss of generality, we may suppose that S = S ∗ and I = I ∗ and we note

$$g_{i}^{*}(J,J_{1})=g_{i}(I^{*},I_{1}^{*},J,J_{1}). $$

Moreover, since the dynamics of I V N does not have any effect on the dynamics of the variables (I 1,J,J 1), we may reduce our analysis to the system of the block (I 1,J,J 1). Finally, since we are interested only on the approximation of the order 1 in ε, we write \(I_{1}(t)=I_{1}^{*}+\varepsilon x(t)\) where \(I_{1}^{*}\) is the stationary solution of the equation of I 1 for ε=0, that is

$$I_{1}^{*}=\frac{\beta S^{*} I^{*}}{m+\beta k I^{*}}=\frac{ (R_{0}-1)}{R_{0}\left( 1+ k(R_{0}-1)\right)}. $$

We will also denote the stationary solution of I 2 = I−I 1 for ε=0 by

$$I_{2}^{*}=I^{*}-I_{1}^{*}=\frac{k\beta (I^{*})^{2}}{m+k\beta I^{*}} = \frac{k(R_{0}-1)^{2}}{R_{0}(1+k(R_{0}-1))}. $$

Using these notations, we focus on the system

$$ \left\{\begin{array}{ll} \frac{d}{dt} x&=-(m+\beta k I^{*})x+ \frac{\beta}{4}g_{0}^{*}(J,J_{1})+O(\varepsilon)\\ \frac{d}{dt} \left( \begin{array}{c}J\\J_{1}\end{array}\right)&=A\left( \begin{array}{c}J\\J_{1}\end{array}\right)+\frac{\varepsilon}{2} k\beta x \begin{pmatrix} 1&0\\0&0\end{pmatrix} \left( \begin{array}{c}J\\J_{1}\end{array}\right) \\ &\phantom{=A\left( \begin{array}{c}J\\J_{1}\end{array}\right)}+\varepsilon \frac{\beta}{4}\left( \begin{array}{c}g_{1}^{*}(J,J_{1})\\g_{2}^{*}(J,J_{1}) \end{array} \right)+O(\varepsilon^{2}) \end{array}\right. $$
(10)

where the linear part of the dynamics of (J,J 1) is given by the matrix

$$A=\left( \begin{array}{ll}\frac{1}{2} k\beta I_{1}^{*}&-\frac{1}{2} k\beta I^{*}\\ m& -(k\beta I^{*}+m) \end{array}\right). $$

The system (10) is not yet written on a slow-fast form. However, the order 0 terms of the dynamics of (J,J 1)t are linear, and independent of x. This implies that the slow and fast directions can be computed by a simple spectral analysis of the matrix A. This matrix has two real eigenvalues: 0 and \(-\mu =tr(A)=\frac {1}{2}k\beta I_{1}^{*}-(k\beta I^{*}+m)<0.\)

Denoting \(V_{\mu }=(I_{2}^{*},2I^{*})^{t}\) and \(V_{0}=(I^{*},I_{1}^{*})^{t}\) the two corresponding eigenvectors, we see that the component y(t) of (J(t),J 1(t))t in the direction of V μ goes exponentially fast to zero, while the component z(t) of (J(t),J 1(t))t in the direction of V 0 varies very slowly. Hence, V μ and V 0 give respectively the fast and the slow directions. The new variables y(t) and z(t) are obtained explicitly from \(J(t) = I_{2}^{*}y(t)+ I^{*} z(t)\) and \(J_{1} (t)= 2I^{*}y(t)+I_{1}^{*}z(t).\) This leads to

$$z=a \frac{J}{I^{*}} +(1-a)\frac{J_{1}}{I_{1}^{*}} $$

with \(a=\frac {2(I^{*})^{2}}{2(I^{*})^{2}-I_{2}^{*}I_{1}^{*}}\in [0,1]\). Since J/I ∗ and \(J_{1}/I_{1}^{*}\) both belong to (−1,1), we get z∈(−1,1). With these new variables, one obtains the explicit slow-fast system:

$$ \left\{\begin{array}{ll} \frac{d}{dt} x&=-(m+\beta k I^{*})x+ \frac{\beta}{4}f_{0}(y,z)+O(\varepsilon)\\ \frac{d}{dt} y&=-\mu y+O(\varepsilon)\\ \frac{d}{dt} z&=\varepsilon \big(f_{2}(x,y,z)+O(\varepsilon)\big) \end{array}\right. $$
(11)

where \(f_{0}(y,z)=g_{0}^{*}\big (I_{2}^{*}y+ I^{*} z,2I^{*}y+I_{1}^{*}z\big )\) and f 2 may be computed explicitly (see Appendix D). At this point, we can apply Tikhonov’s Theorem (Tikhonov 1952). This is done in two steps, as detailed in Supporting Appendices: (i) first, we show that the fast dynamics of the fast variables x and y (taking ε=0) goes exponentially fast in time to a (slow) manifold parametrized by the slow variable z (Appendix B); (ii) secondly, we describe the slow dynamics of z while (x,y) belong to this slow manifold (Appendix C).

Fig. 2
figure 2

The system trajectories (black arrows) reach an ε neighborhood of the slow manifold (in blue) in a time of the order \(O(\varepsilon \ln (1/\varepsilon ))\). Once in this neighbourhood, the trajectories stay ε-close to the slow manifold and follow the slow dynamics, taking a time of order O(ε) to reach the equilibria. Left panel: single colonization variables. Right panel: dual colonization variables

Full size image

The key drivers of slow-fast strain dynamics

Starting with the neutral model, and studying realistic deviations from neutrality, we have obtained a fast and slow component for the dynamics of a multi-strain pathogen system characterized by asymmetric interaction among subtypes in co-colonization. In particular, the dynamics first follow the neutral system, tending to the slow manifold. On this slow manifold, the epidemiological variables are given by

$$ I_{V}= \frac12 I^{*}_{1} (1+z),\quad I_{N}= \frac12 I^{*}_{1} (1-z),\quad I_{VN}= \frac{k R_{0} I^{*}_{1} I^{*}} {2}(1-z^{2}) $$
(12)
$$\begin{array}{@{}rcl@{}} I_{VV}&=&\frac {1+z}{2} I_{2}^{*} -\frac{k R_{0} I^{*}_{1} I^{*}}{4}(1-z^{2}), \quad \text{and} \\ I_{NN}&=&\frac {1-z}{2} I_{2}^{*} -\frac{k R_{0} I^{*}_{1} I^{*}}{4}(1-z^{2}), \end{array} $$

and z remains constant. Once on this slow manifold, the trajectories stay close to this slow manifold and z follows the slow dynamics (Fig. 2), over the time scale τ = ε t. This slow dynamics is given by

$$ \frac{d}{d\tau} z=C({\Theta}-{\Gamma} z)(1-z^{2}),\; z(0)\in[-1,1]. $$
(13)

Thus, we find that two hyper-parameters:

$${\Theta}= \alpha_{VV}-\alpha_{NN}+\left( 1+\frac{2}{k (R_{0}-1)} \right)(\alpha_{NV}-\alpha_{VN}) $$

and

$${\Gamma}=\alpha_{NV}+\alpha_{VN}, $$

govern the asymptotic dynamics of the system for small ε, i.e. for small deviation from neutrality. In the above expressions, \(I_{2}^{*}, I_{1}^{*}\) and their sum I ∗ are derived from the neutral system, and C is a positive constant (see Appendix C), given by:

$$C=\frac{\beta I^{*} I_{1}^{*} I_{2}^{*}}{8(I^{*})^{2}-4I_{1}^{*}I_{2}^{*} }. $$

In particular, C affects the tempo of the slow dynamics. The larger C is, for example the higher the transmission rate β, the faster the slow dynamics are.

From Eq. (13), we can see that the slow dynamics depend nontrivially on the basic reproduction number R 0, the average within-group interaction k, and the relative interaction asymmetries in the α i j . While Γ represents the general dominance of between-group versus within-group interaction, Θ is a function of more parameters, including R 0 and k. More specifically, Θ reflects the hierarchical dominance of one group in the system, in this case V. It comprises a first term that represents Δ s e l f = α V V −α N N , a measure of how different the two groups of pathogen types are in relation to self-interaction. It also comprises a second term Δ n o n−s e l f = α N V −α V N , a measure of how different the two strains are in relation to interaction with n o n−s e l f, i.e. the other group, weighted by a k- and R 0- dependent factor. From the conservation law of the neutral model (Eqs. (3), (4)), this factor can be related to the ratio between dual and single colonization in the symmetric system as follows:

$${\Theta}= {\Delta}_{self}+\left( 1+2 \frac{I_{1}^{*}}{I_{2}^{*}} \right){\Delta}_{non-self}, $$

indicating that it is also the odds in favour of single colonization that amplify the relative importance of cross-group interaction differences Δ n o n−s e l f in the slow dynamics. The reason is that cross-group interaction coefficients effectively modulate the transition from pure single (I V or I N ) to mixed dual colonization (I V N ), thus the more prevalent single colonization is, the more significant become any asymmetries in outward fluxes from this host class favouring one of the two strains. This difference in ‘investment’ in the commonly shared host pool I V N acts to reinforce the net fitness differential and emergent hierarchy between strains at the epidemiological level.

Θ and Γ and the endemic prevalence equilibria

Essentially, Θ and Γ drive the stabilizing forces between strains on the slow manifold. Arising from asymmetric interaction among co-colonizing clones, these forces also configure in detail strain composition at endemic equilibrium. The steady states of the slow variable z can be calculated from solving Eq. (13). They are z ∗=±1 and \(z^{*}=\frac {\Theta }{\Gamma }\). Plugging these solutions into Eq. 12, we recover the endemic equilibria of the original epidemiological system in terms of V and N prevalences. These are described in Fig. 3. The V-N coexistence steady state corresponds to the solution \(z^{*}=\frac {\Theta }{\Gamma }\) which is positive and biologically feasible for \(\left |z^{*}\right |<1\), i.e. \(\left |{\Theta }\right |<\left |{\Gamma }\right |\). Linearization about \(z^{*}=\frac {\Theta }{\Gamma }\) reveals that this steady state is stable whenever Γ>0 (represented by the dark grey region in Fig. 3). The N-only steady state corresponds to the z ∗=−1 solution, while the V-only equilibrium corresponds to the z ∗=1 solution. The latter two solutions may be stable or unstable. The V-only equilibrium is stable for Θ>Γ, while the N-only equilibrium is stable for Θ<−Γ. In particular, a scenario of bistability of the exclusion equilibria (z ∗=±1) arises for Γ<0 and |Θ|<|Γ|, where the coexistence solution \(z^{*}=\frac {\Theta }{\Gamma }\) is unstable.

Fig. 3
figure 3

Graphical summary of the system equilibria for multi-strain dynamics on the slow manifold described by Eq. (13), as a function of the hyper-parameters \({\displaystyle {\Theta }=\alpha _{VV}-\alpha _{NN}+\left (1+\frac {2}{k (R_{0}-1)} \right )}\) (α N V −α V N ) and Γ = α N V + α V N . The insets show the dynamics of the slow variable d z/d τ versus z for canonical cases of Eq. (13). The zero solutions of d z/d τ (z=−1,1,Θ/Γ) correspond via Eq.12 to the endemic equilibria of the original system (N-only, V-only, V-N coexistence). Their stability conditions are illustrated through the different shaded regions. For example, the darker shaded region on top delimits stable V-N coexistence, matching the z ∗=Θ/Γ solution of Eq. (13). The line Θ=0 (Γ>0) corresponds to equal prevalence of the two strains at the epidemiological level, where differences in interaction traits cancel out. This represents maximal diversity and maximal stability of the coexistence equilibrium

Full size image

Thus, all these asymptotic scenarios and their stability properties are determined by the magnitudes of the asymmetries in interaction coefficients, as summarized by Θ and Γ. The stability condition for \(z^{*}=\frac {\Theta }{\Gamma }\), Γ>0, reflects a strong exchange (high inter-connectance) between groups. It becomes evident that stable V-N coexistence is possible only if net exchange between groups is sufficiently high, relative to within-group exchange. Linearization about this equilibrium shows that the stability of V-N coexistence is maximized on the line Θ=0, where the trait differences between pathogen types balance out, and as a result they coexist at equal frequencies.

Inspecting Θ and Γ for special cases yields further insight. For example, the case of equal cross-strain interaction translates to α N V = α V N , and the condition for stable coexistence reduces to |α V N |>|α V V −α N N |/2. We thus recover in our system an analogy with intra- and inter-specific competition driving stable coexistence at higher ecological scales (Tilman 1987). Another feature of the system is that when α N V −α V N >0, Θ decreases as R 0 increases. This means that for the same interaction coefficients between strains, we may move from a V-only endemic state to a coexistence regime, and even to an N-only state, if Θ becomes too low. In other words, just due to altered overall transmission, the epidemiological dominance between strains can shift.

The role of R 0 is evident also in the bistability regime. In our system, bistability occurs when cross-group interaction is weak (relative to within-group interaction) Γ = α N V + α V N <0, and when |Θ|<|Γ|. Such low values of |Θ|, all else equal, could be obtained by increasing the basic reproduction number R 0; in other words, higher transmission intensities would favour bistability over a wider range of weak cross-group interactions. This could be related to an ecological prediction on community assembly processes (Chase 2003), stating that in systems where species inter-connectance rates are low and productivity is high, multiple stable equilibria are more likely than single stable steady states. When the exclusion equilibria are bistable, merely the order of pathogen strains entering a community of hosts can lead to a different final colonization composition. In outcomes depending on initial conditions, stochasticity can play a big role, and in reality, we might observe flips between circulation of one pathogen group, and periods where only the other strain is present, with transient ecological coexistence in between.

Approximation error

Since our approximation is derived from a singular perturbation expansion for small deviation from neutrality, we expect that convergence of the approximation to the exact solution improves as the perturbation becomes smaller and is uniform over all time, as our system does not have chaotic or periodic attractors. Thus, we measure accuracy through the maximum error over all times when approximating five-dimensional trajectories (S equation omitted), similar to the approach by Rossberg and Farnsworth (2011), evaluating aggregation methods for multi-species dynamics. The overall error of our slow-fast approximation is given by:

$$ E= \sqrt{\sum\limits_{i=1}^{5} \max_{t}\bigg(var_{i}^{approx}(t)-var_{i}(t)\bigg)^{2}}, $$
(14)

where variable var is indexed to represent I V (t), I N (t), I V V (t), I N N (t) and I V N (t).

To test the quality of our approximation, we ran trajectories of the original and approximated systems, starting from the slow manifold at the point z(0)=0, for a period of time equal to T=108. As expected, we found that the error tends to zero as ε tends to zero, i.e. as the deviation from neutrality in interaction coefficients decreases. Furthermore, the speed of convergence is independent of R 0 or k (Fig. 4). This illustrates the validity of our approximation, and its robustness to variation in overall intensity of transmission or global interaction strength between types.

Fig. 4
figure 4

As the asymmetries among interaction coefficients vanish 𝜖→0, the error of the slow-fast approximation tends to zero. The different lines depict random combinations of R 0 and k, in the range R 0∈(1,8] and k∈(0,8], and random choice of α i j ∈(−1,1). The simulations were performed with fixed m = μ + γ=0.5, thus different R 0 can be related to variation in transmission rate β

Full size image

Discussion

Microbial pathogens display diversity on many levels, including genetic and antigenic polymorphisms, and are thus bound to be resilient in nature. Understanding the ecology underpinning this diversity is crucial to explain how these systems might respond to human interventions, such as vaccines and drugs (Lipsitch 1997; Martcheva et al. 2008; Colijn and Cohen 2015), and how they might spontaneously evolve (Dercole et al. 2002). We must therefore seek for comprehensive models that can provide mathematical and ecological insight into the short- and long-term dynamics of such systems. On one hand, computer simulations may offer quick illustrations of hypotheses and investigation of scenarios. Yet, they cannot provide a deep understanding, required for successful control. Given the complexity and nonlinearity of such multi-strain systems, approximations are key to maximize insight and explanatory power at minimal complexity.

In this paper, we have presented a new application of singular perturbation theory to analyze the transmission dynamics of an endemic pathogen with multiple interacting subtypes. These dynamics evolve on a fast and slow timescale at the epidemiological level. While the neutral model, based on symmetric interactions upon co-colonization, provides the template of neutrally-stable equilibria for strain coexistence reachable on a fast time scale, the non-neutral model, allowing for asymmetric interactions, captures the slow stabilizing dynamics. Proponents of the neutral theory have recognized that trophically similar species in communities might be ecologically equivalent, at least to a first approximation (Chave 2004; Hubbell 2006). Although the notion that species differences promote coexistence, by inducing stabilizing effects at the community level which is generally accepted, it is still unclear which differences matter for coexistence, or whether differences are necessarily needed for coexistence. The quest is ongoing across systems, from large commensal microbial communities such as the gastrointestinal microbiome (Jeraldo et al. 2012), to pathogens, most-prominently multi-strain systems such as the bacteria pneumococci (Cobey and Lipsitch 2012; Gjini et al. 2016) and dengue viruses (Wearing and Rohani 2006; Mier-y Teran-Romero et al. 2013).

Here, using a simple epidemiological framework, and focusing on direct interaction between strains at co-colonization as our trait of interest, we have addressed the question of which differences matter at the group level, summarizing the slow stabilizing forces with only two hyper-parameters Γ and Θ. In these hyper-parameters, the asymmetries in intra-group and inter-group interactions at co-colonization combine with type-transcending basic reproduction number R 0 and average within-group interaction coefficient k. Asymptotically effective multi-strain coexistence occurs only within certain regions of parameter space, depending on Γ and Θ. However, and most importantly, the slow dynamics, revealed here, details also the transient behaviour of the system, which may be substantially long in the case of related strains. A similar perspective to ours, based on trait asymmetries and slow-fast dynamics, has also been used to analyze the competition between bacterial populations in a chemostat (Rapaport et al. 2009), showing that coexistence of species with similar growth functions can last for a very long time, even when the competitive exclusion principle applies asymptotically.

The present study extends and generalizes findings in (Gjini et al. 2016), by detailing how asymmetric direct interaction (competition/facilitation) between clones at the epidemiological level acts as an alternative route to stabilization of polymorphism in endemic pathogen systems, with the neutral model as a first-order approximation (Lipsitch et al. 2009). When pathogen sub-types are aggregated in two sets, interaction parameters that describe each group might vary with type composition. While the symmetric system accommodates a family of neutrally-stable steady states, realistic small perturbations drive slow stabilizing dynamics nearby, that we have characterized here. Similarly to Adler and Brunet (1991), also modeling interacting strains which alter host susceptibility, we highlight here deviation from neutrality in interaction parameters as a key aspect of the dynamics and of the corresponding model reduction. A difference, however, between our approach and the one by Adler and Brunet (1991) is that our starting aim was not to aggregate the original variables for ultimately working with the reduced model. Starting from the fast-slow dynamic decomposition and the reduced model equations, here we were able to deconvolute the aggregated variables, in order to recover back the original system, including the full resolution of co-colonization. With increasing technologies that can detect and quantify co-occurrence in pathogen systems, there comes greater potential for including its details in theoretical analyses.

Future prospects

Our method can be extended to study various perturbations of the epidemiological system and its relaxation time back to equilibrium, to consider the effects of stochasticity, or of globally changing trends such as a time-varying R 0. Although in our model, we have assumed a constant transmission intensity, this does not exclude the possibility that R 0 may change or fluctuate over time, for example due to weather conditions, seasonality or antibiotic use. Indeed, from the definition of Θ and the equilibria on the slow manifold (Fig. 3), we can see that under fixed interaction parameters, changes in R 0 alone can be sufficient to alter the pattern of dominance among strains at the stable coexistence equilibrium, or even shift the system from stable coexistence to an exclusion state. For such changes in R 0 to effectively impact the slow dynamics, a necessary requirement is that they must occur over a time scale slower than O(ε). Depending on the amplitude and timescale of R 0 variation, interesting effects could emerge. Time-varying R 0 may occur alone or in conjunction with specific interventions such as vaccines that target a subset of pathogen strains. Thus, it is possible that parallel changes in overall transmission, during such targeted vaccination programme, might boost the decline of vaccine subtypes, or counteract it, depending on the underlying interaction strengths between vaccine and non-vaccine strains. The interplay of timescales with regards to R 0 and strain interactions deserves further theoretical investigation, and may turn out especially relevant to explain epidemiological trends across geographical settings, for example of S. pneumoniae serotypes (O’Brien 2008; Moore and Whitney 2008).

In the conservation law, central to our neutral model (fast dynamics), prevalence of susceptible hosts at equilibrium, S ∗, is independent of the interaction parameter k. This is a direct consequence of assuming direct clearance of co-colonization, as opposed to sequential clearance, and is consistent with general strain-transcending immunity. Relaxing this assumption would imply allowing co-colonized hosts to clear one clone at a time and transit into the single colonization class instead. This would make the prevalence of susceptibles in the neutral model a direct function of k, different from the 1/R 0 value in this paper. Application of the slow-fast dynamics approach to this case might prove more difficult since we would lose the triangular block structure of the equations in system (9), but remains of interest for the future.

Although we have considered groups of pathogen subtypes equivalent in most life-history traits, e.g. transmission and clearance rates, a more realistic model could allow for some variation, as in (Adler and Brunet 1991). This would introduce another layer of variability between the two groups, namely in their ability to colonize susceptible hosts, besides simply their ability to co-colonize. Such transmission rate differential would alter the landscape of steady-states, potentially allowing for multistability of alternative coexistence equilibria. Furthermore, the magnitude of such differential (\({R_{0}^{V}}/{R_{0}^{N}}\)) would reshape the slow-fast dynamics decomposition that we obtained here, possibly enabling a third relevant timescale to emerge. This scenario could apply in studies of antibiotic resistance dynamics, where strains may vary in their direct competitive abilities, as well as in their fitness cost of resistance (e.g. lower transmission rate). Co-variation between group-specific R 0 and interaction strengths k i j will likely drive interesting dynamics, enabling exploration of colonization-competition trade-offs.

Our findings may bear relevance also to studies on the evolution of traits modifying competitive performance (Dercole et al. 2002), or the evolution of microbial social interactions (West et al. 2006). The main players in our system are closely related strains, namely equal in all life-history traits, except for slight differences in how they modify the rate of co-colonization in already colonized hosts. This interaction trait, acting both within the same strain and between strains, is shown to critically drive coexistence and transient dynamics between these pathogen types in a population. Viewing these results under the light of microbial life-history evolution, i.e. k i j as representing microbial social interactions, our framework could be useful to study the dynamics of this trait. Once a mutant arises and competes with a resident strain, we obtain the model studied in this paper, where the distance between mutant and resident (𝜖), and the hyper-parameters Θ and Γ need to be considered. The system response to such trait differences could display the slow-fast dynamic characteristics that we have described here. Only in particular cases, the trait differential, combined with R 0 and mean k, should lead to coexistence of the mutant and the resident, each with their own repertoire of ‘social’ behaviours. Besides the final evolutionary outcome, it is important to relate the timescale over which such polymorphisms in social interactions can be maintained, with the magnitude of the polymorphism itself. As ecological interactions in microbial communities often evolve on the same timescales as the species themselves evolve, we must seek to develop frameworks that connect the two. This is an active research field, where mathematical approaches could be useful, especially if integrated with experimental evolution in synthetic or natural microbial communities (Xavier 2011; Widder et al. 2016).

Finally, our model considers a relatively simple ecological scenario (n=2), with only two sets of pathogen subtypes characterized by net pairwise interactions. The next challenge is to extend the slow-fast dynamic decomposition to a higher n. Will multiple nested slow-fast dynamics emerge? Can these be related to previous aggregation frameworks (Adler and Brunet 1991), proposed for multi-strain systems? In reality, we might always want to restrict analysis to a relatively small set of functionally relevant groups of types, defined by taxonomic or antigenic properties, or practical purposes such as types targeted by a vaccine vs. non-target ones. Thus, an explicit resolution at the level of individual types and all their concurrent combinations may not strictly be needed. Generalising our framework to a larger number of competing entities is an exciting avenue for the future, and the basic setup for slow-fast dynamic decomposition that we develop here will provide a useful foundation.