Spillover from marine reserves related to mechanisms of population regulation

Abstract

Spillover of fish from marine reserves to adjacent harvested waters may be mediated by density-independent movement, density-dependent movement, or both. If dispersal is by random movement, populations within the reserve must be regulated by density-dependent population growth (DDG). Density-dependent movement (DDM) can also regulate the population if accelerated emigration from a reserve to the surrounding fishing grounds leads to substantially increased mortality. Using spatially explicit models, we show that stock per unit area is bounded for DDG and increases with size for DDM. With DDG, spillover rate per unit area of reserve is maximized with reserves around 50% larger in linear dimension than the minimum size for population persistence. With DDM, spillover per unit area of reserve increases with reserve size. The results highlight the need for the mechanism of population regulation to be incorporated into theoretical and empirical investigations of marine reserve ecology.

Appendix

This appendix contains analyses to support the findings in Table 1.

Recasting equations in non-dimensional form

Reduction in the DDG model to a non-dimensional form is described by Gurney and Nisbet (1998, pp 53–54). We define base units of length, time, and population density by

$$L_{\text{s}} = \sqrt {\frac{{D_0 }}{r};} {\text{ }}t_{\text{s}} = r^{ - 1} ;{\text{ }}n_{\text{s}} = K$$

(8)

and define dimensionless variables

$$\tilde x = {x \mathord{\left/ {\vphantom {x {L_{\text{s}} }}} \right. \kern-\nulldelimiterspace} {L_{\text{s}} }},\;\tilde y = {y \mathord{\left/ {\vphantom {y {L_{\text{s}} }}} \right. \kern-\nulldelimiterspace} {L_{\text{s}} }},\;\tilde t = {t \mathord{\left/ {\vphantom {t {t_{\text{s}} }}} \right. \kern-\nulldelimiterspace} {t_{\text{s}} }},\;\tilde n = {n \mathord{\left/ {\vphantom {n K}} \right. \kern-\nulldelimiterspace} K}.$$

(9)

The dynamics of the DDG model within the reserve can now be expressed as

$$\frac{{\partial \tilde n}}{{\partial \tilde t}} = \left[ {\frac{{\partial ^2 \tilde n}}{{\partial \tilde x^2 }} + \frac{{\partial ^2 \tilde n}}{{\partial \tilde y^2 }}} \right] + \tilde n\left( {1 - \tilde n} \right)$$

(10)

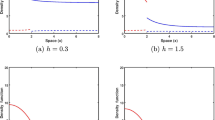
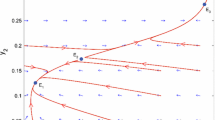
with $\tilde n = 0$ at the reserve boundary. The entire behavior of the system is now determined by a single parameter group $\tilde L = {L \mathord{\left/ {\vphantom {L {L_{\text{s}} }}} \right. \kern-\nulldelimiterspace} {L_{\text{s}} }}$. Because the length scale L _s is proportional to the critical reserve size (see Eq. 7), this implies that the dynamics are controlled completely by the ratio ${L \mathord{\left/ {\vphantom {L {L_{\text{c}} }}} \right. \kern-\nulldelimiterspace} {L_{\text{c}} }}$ used as independent variables in Figs. 2 and 3. The results in Table 1 regarding the dependence of system behavior on parameters other than L (i.e., r, D ₀, K) are obtained by using Eqs. 8 and 9 to convert properties of the dimensionless equations back to the original unscaled variables.

A similar rescaling is used for the DDM model, the only difference being that the base unit of population density is $n_{\text{s}} = {{D_0 } \mathord{\left/ {\vphantom {{D_0 } {D_n }}} \right. \kern-\nulldelimiterspace} {D_n }}$. The DDM model dynamics within the reserve are then described by the equation

$$\frac{{\partial \tilde n}}{{\partial \tilde t}} = \left[ {\frac{\partial }{{\partial \tilde x}}\left( {\left( {1 + \tilde n} \right)\frac{{\partial \tilde n}}{{\partial \tilde x}}} \right) + \frac{\partial }{{\partial \tilde y}}\left( {\left( {1 + \tilde n} \right)\frac{{\partial \tilde n}}{{\partial \tilde y}}} \right)} \right] + \tilde n.$$

(11)

Analysis of DDG model

The steady states of this model have been extensively studied in 1D (Kot 2001, pp 294–301). For any model whose steady states are defined by an equation of the form

$$0 = \frac{{\partial ^2 \tilde n}}{{\partial \tilde x^2 }} + f\left( {\tilde n} \right)$$

(12)

with absorbing boundary conditions at $\pm {{\tilde L} \mathord{\left/ {\vphantom {{\tilde L} 2}} \right. \kern-\nulldelimiterspace} 2}$, there is a first integral

$$\frac{1}{2}\left( {\frac{{\partial \tilde n}}{{\partial \tilde x}}} \right)^2 + F\left( {\tilde n} \right) = F\left( {\tilde n_{\max } } \right)\;{\text{where}}\;F\left( {\tilde n} \right) = \int\limits_0^{\tilde n} {f\left( v \right){\text{d}}v} $$

(13)

and $\tilde n_{\max }$ is the maximum population density (attained at the center of the reserve), and v is a dummy integration variable.

For the DDM model, $f\left( {\tilde n} \right) = \tilde n\left( {1 - \tilde n} \right)$, so $F\left( {\tilde n} \right) = \frac{1}{2}\tilde n^2 - \frac{1}{3}\tilde n^3$. At the reserve boundaries, $F\left( {\tilde n} \right) = 0$, and the total (scaled) spillover rate from the two edges of the reserve is given by

$${\text{Scaled}}\;{\text{spillover}}\;{\text{rate}} = 2\frac{{\partial \tilde n}}{{\partial \tilde x}} = 2\sqrt {2F\left( {\tilde n_{\max } } \right)} $$

(14)

which has a finite upper bound as $\tilde n_{\max } \leqslant 1$. For small reserves (L close to L _c ), the flux is easily shown to be directly proportional to L − L _c . Thus, as L increases, spillover rate per unit length initially rises, then falls asymptotically to zero as L→∞.

For the 2D circular system considered in the paper, we know of no first integral analogous to Eq. 13. In this case, it follows from previous work by Murray and Sperb (1983, p 180) that Eq. 14 is replaced by an inequality

$${\text{Scaled}}\;{\text{spillover}}\;{\text{rate}} = \pi L\sqrt {\left( {\frac{{\partial \tilde n}}{{\partial x}}} \right)^2 + \left( {\frac{{\partial \tilde n}}{{\partial y}}} \right)^2 } \leqslant \pi L\sqrt {2F\left( {\tilde n_{\max } } \right)} .$$

(15)

For small reserves (L close to L _c), the flux is easily shown to be directly proportional to $\left( {L - L_{\text{c}} } \right)^2$. Thus, spillover rate per unit area will have a unimodal form analogous to the 1D situation. This was demonstrated numerically in Fig. 3c.

Analysis of the DDM model

A change of variable transforms the scaled DDM in 1D to the form in Eq. 12. If we define

$$u = \tilde n + \frac{1}{2}\tilde n^2 ,$$

(16)

then, after some algebra, we obtain

$$0 = \frac{{\partial ^2 u}}{{\partial \tilde x^2 }} + f\left( u \right)\;{\text{with}}\;f\left( u \right) = - 1 + \sqrt {1 + u} \;$$

(17)

The maximum value of u (attained at the center of the reserve) is related to the scaled size by (cf. Kot 2001, Eq. 17.17)

$$\tilde L = 2\int\limits_0^{u_{\max } } {\frac{{{\text{d}}u}}{{\sqrt {F\left( {u_{\max } } \right) - F\left( u \right)} }}} \;{\text{with}}\;F\left( u \right) = \int\limits_0^u {f\left( v \right){\text{d}}v} $$

(18)

In contrast with the DDG case, there is no upper bound to u _max for the DDM model, and with some algebra, it can be shown that as L→∞, $u_{\max } \propto L^4$. To see this, first note from Eqs. 17 and 18 that

$$F\left( u \right) = - u + \frac{2}{3}\left( {1 + u} \right)^{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \sim \frac{2}{3}u^{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \;{\text{as}}\;L \to \infty .$$

(19)

Then, substitute $z = {u \mathord{\left/ {\vphantom {u {u_{\max } }}} \right. \kern-\nulldelimiterspace} {u_{\max } }}$ in Eq. 18 to obtain

$$\tilde L = 2\int\limits_0^{u_{\max } } {\frac{{du}}{{\sqrt {F(u_{\max } ) - F(u)} }}} \propto u_{\max } ^{1/4} \int\limits_0^1 {\frac{{dz}}{{\sqrt {1 - z^{3/2} } }}} .$$

(20)

The last integral does not involve u _max, so the result follows.

Equation 16 then implies that the maximum scaled population density $\tilde n_{\max } \propto L^2$, and hence total population size (TPS) is proportional to L ³. In this model, spillover rate is proportional to TPS, so spillover rate per unit length increases as the reserve increases, and there is no optimum reserve size that maximizes spillover.

We are unable to construct a proof of the analogous result for 2D because of the lack of a simple first integral (the use of the Murray–Sperb inequality does not help here), but the very strong 1D result makes very plausible our numerically-based conclusion that there is no optimum reserve size for DDM.