Introduction

Powder bed fusion (PBF) additive manufacturing (AM)1,2 enables fabrication of a three-dimensional (3D) metallic component in a layer-by-layer fashion. The process involves local delivery of powder feedstock, its selective melting by a heat source (laser or electron beam) (see Fig. 1a), and subsequent solidification of the molten material, which fuses to the layer below. This manufacturing technique results in highly complex geometries hardly machinable using conventional subtractive and formative manufacturing approaches. As a result, metal powder bed fusion is continuing to gain importance across a diverse application space, such as aerospace, transportation, and medical applications to name but a few.1

Fig. 1
figure 1

(a) The dominant physical phenomena (such as heat transfer, molten pool fluid flow, and phase transitions); (b) thermal cycles at a monitoring location highlighted by a dashed square in (a); (c) the attending solidification of β phase and (d) precipitation of α and/or α′ from β matrix during powder bed fusion additive manufacturing

Full size image

Ti-6Al-4V (Ti-64) is the single most extensively studied alloy in metal AM.3,4,–5 Similar to conventionally manufactured Ti-64,6 the microstructures in additively manufactured Ti-64 microstructures consist primarily of two simple phases: a high-temperature β phase that has a body-centered cubic structure, and a low-temperature α(α′) phase that has a hexagonal close-packed structure. Depending on whether the powder bed temperature is above or below the α′ martensitic transformation (Ms = 575°C7), the resulting precipitate microstructure varies from the equilibrium α precipitate (e.g., in Ti-64 fabricated by electron beam-based AM approaches8) to acicular α′ martensite, e.g., in Ti-64 fabricated by laser-based AM approaches such as laser power bed fusion (LPBF) AM.9 In general, the primary β solidification grain structures (size, morphology, and crystallographic texture) govern the ductility, while the α(α′) second-phase precipitate microstructure features such as volume fraction, size, shape, orientation, coherency state, and spatial distribution profoundly influence the deformation mechanisms and thus strength.

However, the microstructures in additively manufactured Ti-64 are complex, often exhibiting spatially variable features within a build.2,10 Taking LPBF additive manufacturing as an example, three unique attributes of the process contribute to the microstructure inhomogeneities: First, LPBF is fundamentally a highly localized solidification process. The evolution of the β phase grain structure and the solidification morphology are governed by the shape and size of the moving melt pool. Columnar grains tend to grow from the boundary toward the center of the melt pool along the maximum heat flow direction, which is perpendicular to the solidifying surface of the melt pool (see Fig. 1c). The geometrical features of the melt pool are influenced by the flow of the liquid metal due to the surface tension gradient on the top surface of the melt pool and the recoil pressure (see Fig. 1a). Second, the underlying layers from previous scan cycles are subjected to repeated heating and cooling during deposition of successive layers; see Fig. 1b as an example, in which the first and the strongest peak corresponds to a position of the laser beam just above the monitoring location, while the subsequent weaker peaks occur during the deposition of the successive layers. These repeated thermal cycles affect not only the β grain structure due to both partial melting of the grains in the previous layer and the curvature-driven grain growth in the solid state, but also the second-phase α(α′) precipitate microstructure. Upon further cooling, the microstructures change from colony, basket weave Widmanstätten α structure to martensitic α′ depending on the cooling rate; upon heating, the α precipitates will dissolve in the β matrix or transform back to the β phase if the temperature exceeds the β transus temperature (Tβ). The martensitic α′ may decompose, resulting in the formation of a fine lamellar α/β structure.3 Third, the spatially variable nonlinear time–temperature profile results in a location-dependent, inhomogeneous microstructure and properties. Spatial variation of the local temperature gradient and solidification growth rate, which determine the solidification morphology and direction of maximum heat flow from the melt pool to the substrate or the underlying layer, occurs in different layers of the deposit.1,2

This hierarchical microstructure, including texture, grain size, and morphology, and the number density and size distribution of (meta)stable precipitates, is intimately affected by the thermal profile.10,11 This is determined in a complex way by the choice of several LPBF process parameters, mainly laser power, laser scan speed, and scan strategy, as well as the choice of the powder size distribution and powder bed thickness. Since LPBF is a highly transient process with multiple complex physical effects (violent melt flow, evaporation, rapid solidification, and thermal cycling, to name but a few) that combine to offer a challenging optimization problem, it is difficult to develop fundamental and comprehensive understanding of the AM process and its influence on microstructural evolution and related properties by experimental study alone.12,13

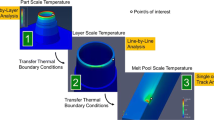
The primary goals of the present work are to (a) develop a rigorous and realistic framework to predict microstructure evolution during the entire LPBF-AM cycle (including powder melting, solidification, and subsequent cooling and reheating), and (b) carry out a parametric study to correlate microstructures developed and resulting mechanical properties with the unique thermal history of the AM process. The key microstructures to be simulated include: the solidification β grain structure and the solid-state second-phase α(α′) precipitate microstructure. As shown in Fig. 2, the modeling framework is developed on the basis of the interaction between (a) an arbitrary Lagrangian–Eulerian (ALE)-based powder-scale model to predict spatiotemporal evolution of thermal history,12 (b) a cellular automaton (CA)14 model to simulate grain structure evolution (size as well as orientation), and (c) a quantitative phase-field (PF)15,16 model to predict the subgrain/intragranular precipitate microstructure.

Fig. 2
figure 2

An integrated multiscale modeling framework to predict microstructure evolution during the entire AM cycle, developed on the basis of the interaction among (a, b) an arbitrary Lagrangian–Eulerian (ALE)-based powder-scale model to predict spatiotemporal evolution of thermal history, (c) a cellular automaton (CA) model to simulate solidification grain structure evolution (size as well as orientation), and (d) a quantitative phase-field (PF) model to predict the subgrain/intragranular solid-state precipitate microstructure

Full size image

We apply our integrated framework by simulating the melt pool in a single-laser-track LPBF of Ti-64 powder followed by consideration of the solid microstructure. In addition, the simulated α + β microstructure is used as an input for a full-field microstructure-based effective elastic modulus calculation to investigate the influence of microstructure inhomogeneity on the resulting mechanical properties. This integrated modeling framework for accurately predicting the thermal fields and histories, and thereby controlling microstructures, is expected to enable engineering location-specific properties in an additively manufactured build.

Multiphysics and Multiscale Modeling Framework

3D Transient Temperature Fields and Melt Pool Geometries

Three-dimensional (3D), transient temperature fields and melt pool dynamics during single-track LPBF of Ti-64 are obtained by solving the equations of conservation of mass, momentum, and energy. This is carried out by using the ALE3D code,17,18 a multiphysics numerical software tool developed at Lawrence Livermore National Laboratory utilizing arbitrary Lagrangian–Eulerian techniques. The code addresses the three-dimensional model using a hybrid finite element and finite volume formulation on an unstructured grid.

The powder bed considered in the simulation is 760 μm long, 260 μm wide, and one layer thick (~ 40 μm), sitting on a 220-μm-thick substrate. Random particle packing (45% density) and the particle size distribution are modeled using the ALE3D utility code, ParticlePack. A laser track with two different processing parameters are considered: a power (p) of 75 W and scanning speed (s) of 500 mm/s (referred to as p75s500 hereafter), and a power 200 W and scanning speed of 1300 m/s (referred to as p200s1300 hereafter). Thus, the energy density Q is the same for the two parameter sets, being defined as Q = P/vtwb, where P, v, t, and wb denote laser power, scan speed, powder layer thickness, and beam size, respectively. The study uses a ray-tracing laser source that consists of vertical rays with a Gaussian energy distribution (D4σ = 57 μm). The model output provides the transient temperature field throughout the entire build from melting to solidification and serves as input for the CA simulation of solidification grain structures (see Fig. 2a).

The quality of our framework’s prediction relies on an accurate thermal profile. This is achieved by incorporating the main physical effects acting on the temperature in the melt pool. This requires a high degree of fidelity19 by accounting for multiple, closely coupled physical processes operating simultaneously during the LPBF process, which all have a strong dependence on temperature. The processes include Marangoni convention (driven by the temperature-dependent surface tension of the melt) and the depression of the melt pool surface below the laser spot (caused by recoil pressure due to vaporization of the melt), both having significant effects in shaping the melt pool flow and thus heat transfer. The latter, if too strong, could create pores as well. Moreover, the incorporation of the contribution from an evaporative cooling caps the maximum melt surface temperature under the laser. Furthermore, instead of using traditional volumetric energy deposition, the utilization of laser ray-tracing energy deposition in the model allows the consideration of partial melting, which contributes to the formation of pore defects in the denudation zone.

Cellular Automaton (CA) Simulation of Solidification Grain Structures

The CA algorithm consists of two main phases: nucleation and growth.14,20,21 In nucleation, different cells are randomly chosen to act as nucleation sites. However, no nucleation takes place in the melt pool, since Ti-64 does not produce equiaxed grains during AM.2 Thus, the main simulated microstructure evolution consists of epitaxial growth from the previous underlying grains in the substrate. This growth is governed by a cellular automata-like set of rules. Instead of simulating the complex development of the dendritic patterns (e.g., network of dendrite trunks and arms), the method simulates the development of the external envelope of each dendritic grain using simplified growth kinetic laws. The envelope can be used to represent any other developing structure, including planar and cellular, as long as the time-dependent growth velocity is accounted for. In 3D, the envelope is a regular octahedron whose center is located at the center of a CA cell. Each octahedron grows along its main diagonals corresponding to the \( \left\langle {001} \right\rangle \) crystallographic orientations of the dendrite. Apices of the octahedron correspond to the leading dendrite tips of the crystal. The position of apices defined by the half-diagonal are updated at a velocity v(ΔT), which depends on the undercooling of its cell approximated by a polynomial law:22

$$ v\left( {\Delta T} \right) = a_{1} \cdot \Delta T + a_{2} \cdot \left( {\Delta T} \right)^{2} $$
(1)

where ΔT is the undercooling below the liquidus temperature Tm and the coefficients are material-dependent parameters, taken from Refs. 22 and 23 for the current study.

Once an octahedron grows large enough to encompass the center of a neighboring undercooled liquid cell, this neighboring cell (μ) is then captured. The captured cell μ inherits the grain properties (i.e., grain identification number and orientation) from the capturing cell. A new, smaller octahedral envelope is created at the cell μ, with its size and center determined according to the decentered octahedron algorithm,14 which prevents mesh imprinting on the grain growth. All liquid cells with ΔT > 0 are successively scanned for capture by their direct neighbors, i.e., 26 neighbors in 3D. Octahedra grow independently until all neighboring cells are captured.

The main input to the method is the thermal profile, which is taken from the coarse FE mesh and projected onto the finer CA mesh. Temperature fields are interpolated between the FE mesh and the CA mesh. A CA grid made of a regular lattice of cubic cells is defined and superimposed onto the CA mesh. The size of the CA grid used is 380Δx × 130Δy × 180Δz with grid size of Δx = Δy = Δz = 2 μm, which corresponds to 760 μm × 260 μm × 360 μm. The thickness of the original substrate along the z direction is 220 μm.

Phase-Field Simulation of α Precipitation Upon Continuous Cooling

Phase-Field Model

A three-dimensional multi-phase field model for an elastically and structurally inhomogeneous system15,16 is employed to simulate microstructural evolution (α precipitation) in a bicrystalline Ti-64. In this approach (Fig. 2d), an arbitrary α + β two-phase microstructure in the ternary Ti-64 system is characterized by two concentration fields (i.e., conserved order parameters), \( \left\{ {X_{i} \left( {\mathbf{r}} \right)} \right\}_{{i = {\text{Al, V}}}} \), and 12 structural order parameters (i.e., nonconserved order parameters), \( \left\{ {\phi_{p} \left( {\gamma ,{\mathbf{r}}} \right)} \right\}_{p = 1 }^{12} \left( {\gamma = \beta_{i = 1 \ldots N} } \right) \), within each prior β grain (where N denotes the total number of prior β grains). Both conserved and nonconserved order parameters vary continuously across the α/β interfaces. Even though the β phase grain structure can be taken directly from a representative volume element from the CA simulation, here for simplicity, we consider a bicrystalline β sample. The bicrystal is constructed by first halving the perfect crystal along the (010)β plane and rotating the two resulting grains by 10.52° for β2 on the left-hand side and – 5.26° for β1 on the right-hand side, around the [101]β direction. The total free energy of the system, F, is formulated as a functional of these two sets of order parameters. The phase-field model associated with the precipitation process has been employed in our previous works,15,16 to address the influence of applied stress/strain and grain boundary dislocation on variant selection of α precipitates upon isothermal aging. The only difference in the methodology is the replacement of Langevin noise terms in the governing equations by the explicit nucleation algorithm to account for the nucleation process under continuous cooling conditions, as described in detail in “Explicit Nucleation Algorithm” section. Therefore, here we omit the model framework and formulation, which can be found in Refs. 15 and 16 (e.g., chemical free energy, elastic strain energy of elastically and structurally inhomogeneous solid) and only specify the kinetic governing equations that describe the microstructure evolution represented by the temporal and spatial evolution of both conserved and nonconserved order parameters, as follows:

$$ \frac{{\partial X_{i} \left( {{\mathbf{r}},t} \right)}}{\partial t} = \nabla M_{c} \nabla \frac{\delta F}{{\delta X_{i} }} $$
(2)
$$ \frac{{\partial \phi_{p} \left( {{\mathbf{r}},t} \right)}}{\partial t} = - M_{\phi } \nabla \frac{\delta F}{{\delta \phi_{p} }} $$
(3)

where Mc and Mϕ denote the chemical mobility and the mobility of the order parameter, respectively. The former links directly with an atomic mobility database, while the latter is determined to guarantee a diffusion-controlled process. The size of the computation cell we considered is 256Δx × 128Δy × 64Δz. with grid size of Δx = Δy = Δz = 12.5 nm, which corresponds to 3.2 μm × 1.6 μm × 0.8 μm. The grain boundary is placed along the yz plane at x = 128Δx.

Explicit Nucleation Algorithm

Microstructure development under nonisothermal conditions involves concurrent nucleation, growth, and coarsening (i.e., nucleation may occur while other particles are growing). Nucleation needs separate treatment, as the phase-field kinetics equations (Eqs. 2 and 3) are driven by total free energy reduction. This excludes any activation process, which requires a temporary increase in total free energy. The use of the conventional Langevin force terms in Eqs. 2 and 3 for nucleation in mesoscale microstructural simulations is qualitative in nature, and its applications are limited to site-saturation conditions. In the present work, nucleation is implemented though an explicit nucleation algorithm (ENA)24,25,26,–27 that stochastically seeds nuclei in an evolving microstructure according to a nucleation rate assessed as a function of local temperature, concentration, and crystalline defects (such as dislocations and grain boundaries). As compared with the traditional Langevin force approach, ENA allows for consideration of nucleation events that may occur at any time whenever the driving force permits.24

By treating a local nucleation event as a thermally activated process, the nucleation rate is given by

$$ \varvec{J}\left( {{\mathbf{r}},t} \right) = \varvec{J}_{0} \left( {{\mathbf{r}},t} \right){ \exp }\left( { - \Delta G^{*} \left( {{\mathbf{r}},t} \right)/k_{\text{B}} T} \right) $$
(4)

where J denotes the rate of either homogeneous Jhom or heterogenous Jhet nucleation with the respective prefactors \( \varvec{J}_{0}^{ \hom } \) and \( \varvec{J}_{0}^{\text{het}} \) on the right-hand side of Eq. 4. ΔG* represents the activation energy barrier of homogeneous \( (\Delta G_{ \hom }^{*} ) \) and heterogeneous nucleation \( (\Delta G_{\text{het}}^{*} ) \). In the same equation, kB is Boltzmann’s constant and T is absolute temperature.

Nucleation events are explicitly introduced into the matrix through a probabilistic Poisson seeding process at a probability of forming a critical nucleus:

$$ P\left( {{\mathbf{r}},t} \right) = 1 - \exp \left( { - \varvec{J}\left( {{\mathbf{r}},t} \right)\Delta V\Delta t} \right) $$
(5)

where P is the probability of forming a critical nucleus in a volume ΔV and a time interval Δt, which are predefined according to the length and time scale of the model. To actuate a nucleation event, at each time step, a random number, Pr, with uniform distribution between 0 and 1, is generated for each untransformed phase-field cell. A phase-field cell is considered to transform provided that P > Pr. If a nucleation event is determined to occur, an overcritical α nucleus of its equilibrium composition will be introduced to the computational cell. To ensure mass conservation, a solute depletion zone in the adjacent β matrix is also considered. The size and composition within the depletion zone are determined according to Zenner approximation.28 If nucleation occurs at a grain boundary (GB), α nuclei are introduced in the form of a spherical cap.

From Eq. 5, ENA does not specify the method for computing the activation energy of nucleation ΔG* in Eq. 4, which offers the flexibility to choose any state-of-the-art nucleation theory available for the model. Here, the classical nucleation theory (CNT) is employed. By assuming a spherical critical nucleus, \( \Delta G_{ \hom }^{*} = 16\pi \sigma^{3} /3\left( {\Delta G_{\text{V}} } \right)^{2} \), where σ is the interface energy associated with the coherent α/β interface and ΔGV is the chemical driving force for nucleation as a function of alloy composition and temperature, computed on the fly using the available thermodynamic database for Ti-64.

The prefactor in Eq. 4 for homogeneous nucleation is given by

$$ \varvec{J}_{0}^{\hom } \left( {{\mathbf{r}},t} \right) = N_{0} Z\beta^{*} $$
(6)

where N0 (units: # m−3) is the number of available nucleation sites per unit volume. Z is the dimensionless Zeldovich factor, used to measure the probability that a supercritical nucleus with radius slightly larger than the critical radius passes back across the free energy barrier and dissolves in the matrix, being related solely to the thermodynamics of the nucleation process. β* is defined as the rate at which atoms or molecules are attached to the critical nucleus and so quantifies the kinetics of mass transport in the nucleation process. The values of Z and β* in Eq. 6 are calculated by linking with the thermodynamic and kinetic databases of Ti-64.29 For heterogenous nucleation at a GB, \( J_{0}^{\text{het}} \left( {{\text{r}},t} \right) \) is related to \( J_{0}^{ \hom } \left( {{\text{r}},t} \right) \) by \( J_{0}^{\text{het}} \left( {{\text{r}},t} \right) = \delta /DJ_{0}^{ \hom } \left( {{\text{r}},t} \right) \), where δ and D denote grain boundary thickness and average grain boundary length, respectively.

Numerical Evaluation of Micro- and Mesoscopic Elastic Properties of AM Microstructures

To evaluate the elastic behaviors of complex AM microstructures, we compute: (1) the microscopic local stress field under applied load, and (2) the corresponding effective elastic moduli. We employ a numerical method similar to that described in Ref. 30 based on the Fourier-spectral iterative perturbation method.31,32 We first take final (α + β) two-phase microstructures generated by phase-field simulations under different cooling rates as described in “Phase-field Simulation of α Precipitation Upon Continuous Cooling” section as inputs. Note that these two-phase microstructures are elastically inhomogeneous since the heterogeneously distributed two phases have different elastic properties. Therefore, the local elastic response of the microstructures to the applied load is nontrivial, leading to a nonuniform distribution of local stress/strain fields. This may lead to local regions incorporating highly concentrated stresses, so-called stress hotspots.33

To capture the elastic inhomogeneity, we assign elastic moduli of α and β phases to corresponding parts in the polycrystalline two-phase microstructure by the following elasticity model:34

$$ \varvec{C}_{ijkl}^{\text{total}} \left( {\mathbf{r}} \right) = \mathop \sum \limits_{g} \theta \left( g \right) \cdot a_{ip}^{g} \cdot a_{jq}^{g} \cdot a_{kr}^{g} \cdot a_{ls}^{g} \cdot \varvec{C}_{pqrs}^{\text{Ti64}} \left( {\mathbf{r}} \right) $$
(7)

where θ(g) is the grain shape function (θ = 1 within the gth β grain and θ = 0 outside), \( a_{ip}^{g} \) (i, p = 1–3) is the transformation matrix describing the grain orientation, and \( \varvec{C}_{pqrs}^{\text{Ti64}} \) is the phase-dependent elastic modulus of two-phase Ti-64 defined on the reference grain. This phase-dependent modulus is modeled as: \( \varvec{C}_{ijkl}^{\text{Ti64}} = (1 - \sum\nolimits_{p = 1}^{12} {h(\phi_{p} )} ) \cdot \varvec{C}_{ijkl}^{\beta } + \sum\nolimits_{v = 1}^{12} {h(\phi_{p} )} \cdot \varvec{C}_{ijkl}^{\alpha } (p) \), where \( \varvec{C}_{ijkl}^{\alpha } \) and \( \varvec{C}_{ijkl}^{\beta } \) are the elastic moduli of α and β phase, respectively, ϕp are the order parameters identifying α variants, and \( h(\phi ) \equiv \phi^{3} (6\phi^{2} - 15\phi + 10) \) is the interpolation function. The elastic moduli for the individual α and β phases were taken from Ref. 35.

Employing the inhomogeneous elasticity model described above, we numerically solve the mechanical equilibrium equation under applied loads as follows:

$$ \nabla_{j} \sigma_{ij} \left( {\mathbf{r}} \right) = \nabla_{j} \left[ {\varvec{C}_{ijkl}^{\text{total}} \left( {\mathbf{r}} \right) \cdot \epsilon_{kl}^{\text{el}} \left( {\mathbf{r}} \right)} \right] = 0 $$
(8)

where σij (i, j = 1–3) is the stress tensor and \( \epsilon_{kl}^{\text{el}} \) is the elastic strain tensor. By solving Eq. 8, we obtain the microscopic stress and strain profiles over the employed complex microstructure. In addition, we can extract the effective elastic modulus \( \varvec{C}_{ijkl}^{\text{eff}} \) of the two-phase Ti-64 microstructure using the following equation: \( \sigma_{ij}^{\text{avg}} = C_{ijkl}^{\text{eff}} \cdot \bar{\epsilon }_{kl} \), where \( \sigma_{ij}^{\text{avg}} = (1/V)\int_{V} {\sigma_{ij} ({\mathbf{r}}){\text{d}}V} \) is the average stress over the complex microstructure when the applied strain \( \bar{\epsilon }_{kl} \) is imposed. The computed effective modulus represents the collective/macroscopic elastic response of the nonuniform two-phase microstructure.

Results and Discussion

CA Simulations of Solidification Grain Structure

We first study the development of solidification grain structure in a single-layer sample of Ti-64 deposited in a single laser track to identify key features of grain structure formed. The prior β grain structure in the substrate, created using DREAM.3D,36 is fully equiaxed with random crystallographic orientation (there are 22,496 grains in total with average grain size of 22.6 μm).

Figure 3 shows the evolution of the computed temperature distribution in the part (left column) and the attending grain structure (right column) in the track. Only one longitudinal half-slice of the track is presented to show the temperature fields and grain structures on the surface and in the interior. Inside the melt pool (bounded by the black contour line indicating liquidus temperature), the temperature is highest near the heat source and lowest near the boundary of the pool.

Fig. 3
figure 3

Time snapshots showing the evolution of thermal profile (left column: (a) t = 327 μs, (c) t = 647 μs, (e) t = 967 μs) and grain structure (right column: (b) t = 327 μs, (d) t = 647 μs, (f) t = 967 μs) during a single-track L-PBF AM of Ti-64. The laser scan speed is 500 mm/s, moving to the right with a power of 75 W. In the left column, the red pseudocolor corresponds to temperature scale capped at 3200 K, where blue is 298 K. The black contour line denotes the melting temperature line, T = 1923 K. In the right column, grains are visualized with the inverse pole figure coloring scheme. The liquid molten pool is visualized in red. Reference frame: X, scanning direction; Y, transverse direction; Z, build direction (Color figure online)

Full size image

During the deposition of the first layer, the substrate below is partially remelted and resolidified. As the laser moves away, cooling and solidification of the fusion zone occur. The grains produced during solidification grow epitaxially from the partially melted prior equiaxed grain in the substrate (Fig. 3b). Epitaxial grain growth initiates at the fusion line and tends to grow normal to the moving solidification front (i.e., the local maximum temperature gradient), leading to the formation of columnar grains (Fig. 3d and f). The direction of the thermal gradient (i.e., maximum heat flow direction) in the melt pool is perpendicular to the boundary of the melt pool at the trailing edge. For a continuously moving melt pool, the maximum heat flow direction changes as the pool progresses. See the variation of melt pool size, geometry, and local curvature as shown in Fig. 3a, c, and e.

The formation of the grain structure is also demonstrated in three two-dimensional (2D) cross-sections, including a horizontal slice (at 14 μm below the surface of the original substrate, left column of Fig. 4), longitudinal slice (through the center of the simulation box, right column of Fig. 4), and transverse slice (at X = 450 μm, as indicated by the vertical dashed line in Fig. 4a). The trapped pores formed in the melt track are shown in green.

Fig. 4
figure 4

Sequence of images depicting grain structure evolution. Left column: top-down view at 14 μm below the original substrate surface, (a) horizontal slice at t = 0 μs, (c) t = 327 μs, (e) t = 647 μs, and (g) t = 967 μs; Right column: longitudinal slice through the center of the simulation box, (b) longitudinal slice at t = 0 μs, (d) t = 327 μs, (f) t = 647 μs, and (h) t = 967 μs; Bottom row: transverse cross-section at X = 450 μm at (i) t = 807 μs, (j) t = 967 μs, and (k) t = 1127 μs. Grains in the original substrate are colored in light blue, with corresponding grain boundaries (GBs) in black. New grains generated by nucleation in the melt pool during scan are colored using inverse pole figure color scheme with corresponding GBs colored in dark red. Cells in liquid state and their boundaries are colored in red, indicating the boundary of melt pool. Cells filled by vapor (i.e., pores) and their boundaries are colored light green. Curved white dashed lines in (g), (h), and (k) indicate the fusion boundary (Color figure online)

Full size image

Epitaxial growth of grains near the melt pool boundary proceeds by shifting their growth directions to align with the temperature gradient, which is normal to the melt pool boundary. The local growth direction shown is spatially changing during the movement of the melt pool, depending on the 3D temperature gradients, which affects the local curvature of the solidification interface. Thus, it appears macroscopically that the curved columnar grains are pulled by the curvature of the trailing edge of the melt pool, as shown in both horizontal and longitudinal slices. The microstructure near the fusion line is influenced by the substrate (dashed lines in Fig. 4g and h). However, further away from the fusion line, the microstructure is governed by the competitive growth of grains with various crystallographic orientations in the polycrystalline substrate. Grains with preferential growth directions (i.e., \( \left\langle {100} \right\rangle \) for metals with bcc structure) more aligned with the temperature gradient outgrow slower-growing misaligned grains, leading to the development of a columnar structure. Such a competitive growth mechanism can be observed in Fig. 4h, where grain A is outgrown by the more favored grain B.

The transverse cross-sections in the bottom row of Fig. 4 show another distinct growth pattern: the grains adopt a radial growth direction toward the top center of the melt pool. The columnar grains grow as the bottom of the melt pool moves upwards during the subsequent cooling process. The simulation results show that the columnar grains grow continuously from the fusion zone boundary towards the curved top surface of the deposit. Near the melt pool boundary (dashed line in Fig. 4k), the grain growth direction is approximately in plane within the transverse section, because columnar grain growth occurs perpendicular to the melt pool boundary. However, in other parts of the sample, the grain growth is out of plane, so the full length of the columnar grains is not observable. Although many grains in the resolidified zone may look equiaxed, they are actually columnar grains growing into the cross-section plane. It is important to note that, when performing experimental electron backscatter diffraction (EBSD) cross-section measurements, transverse slices could incorrectly imply equiaxed grain growth, when in reality, the observed texture is caused by these columnar grains that are extending across the plane of the measurements.

The melt pool geometry as a function of processing parameters is presented in Fig. 5. Two scanning speed are selected: 500 mm/s and 1300 mm/s, with respective laser power of 75 W and 200 W. Comparing Fig. 5a and b, an increased scanning speed (while keeping the energy density the same) results in a more elongated melt pool shape. As shown in Fig. 5c, the curvature at the trailing edge of the melt pool is reduced, and in particular, the bottom of the elongated melt pool is nearly horizontally oriented due to fast scanning (Fig. 5d). Thus, the columnar grains grow epitaxially from the substrate, along the bulid direction, which is perpendicular to the bottom of the melt pool.

Fig. 5
figure 5

Comparison of melt pool geometry as a function of processing variables: laser power (p) and scanning speed (s): (a) p75s500: horizontal slice; (b) p200s1300: horizontal slice; (c) longitudinal slice; (d) longitudinal slice at t = 483 μs

Full size image

The difference in the melt pool geometry (size and shape) results in different grain orientations, as demonstrated in Fig. 6. The resulting grain structures are compared in the horizontal, transverse, and longitudinal sectional planes. In the melted and resolidified regions (highlighted by the dashed lines), grains are columnar with elongation observed on all three cross-sections. From the top-down view, in the case of p200s1300, grains develop a shape with a main elongation direction normal to the moving direction of the heat source, i.e., the transverse or Y-direction. They are terminated at the center line (horizontal dashed line in Fig. 6b). With decreased scanning velocity (i.e., p75s500), the columnar grains appear tilted and seem to follow the trajectory of the heat source, as shown in Fig. 6a, not being interrupted by other grains developing on their side. Since these grains tend to follow the trajectory of the heat source, they appear small and more evenly distributed in the transverse cross-section perpendicular to the movement of the heat source (Fig. 6c), as compared with the case of p200s1300 (Fig. 6d). From the longitudinal cross-section, the columnar grains tend to align along the build direction with increased scanning speed (Fig. 6f) as compared with the case with reduced scanning speed. To demonstrate the trend, the inverse pole figure of the longitudinal slice is presented, where the build direction (BD) is projected to the crystal reference frame of grains. As shown in Fig. 6g, \( \left\langle {111} \right\rangle \) directions of the columnar grains align preferentially along the BD in the case of p75s500, which indicates that the preferred grow directions, \( \left\langle {100} \right\rangle \), make a certain angle with the BD. In contrast, the columnar grains in the case of p200s1300 grow epitaxially from the substrate, preferentially along the build direction, which is perpendicular to the bottom of the melt pool. The trends shown in the present simulations agree well with those commonly observed in literature on grain structure evolution in fusion welding processes.37,38

Fig. 6
figure 6

Resulting solidification grain structure (in three different cross-sections) as a function of laser power (p) and scanning speed (s): (a) p75s500: horizontal slice; (b) p200s1300: horizontal slice; (c) p75s500: transverse slice; (d) p200s1300: transverse slice; (e) p75s500: longitudinal slice; (f) p200s1300: longitudinal slice; (g) inverse pole figure of (e); (h) inverse pole figure of (f)

Full size image

Phase-Field Simulations of α Precipitation Upon Continuous Cooling

Different scan strategies in LPBF can lead to varying thermal histories that differ between laser scanned tracks and layers. Volume elements in different layers are subjected to different numbers of thermal cycles during processing, each of which may have a different peak temperature and time duration, leading to significant spatial heterogeneity in the microstructure. It is then advantageous and possible to control these variations in the microstructure through optimization of the scan strategy, or more generally, through optimized control over the thermal history. In this work, we investigate the influence of the cooling rate experienced by different volume elements on the key precipitate microstructure features, i.e., the density and spatial uniformity of the α precipitate.

Figure 7 shows α precipitation upon cooling at a rate of 5°C/s from a temperature (950°C) above the β transus temperature to 700°C (above Ms = 570°C). The rates of both homogeneous (Jhom) and heterogeneous (Jhet) nucleation of α phase in Ti-6Al-4V are shown as functions of temperature in Fig. 7a. The shape of the distribution is determined by the temperature dependence of the nucleation prefactor (Eq. 3) and nucleation barrier. Both Jhom and Jhet increase sharply with cooling (increased undercooling), and eventually decrease at low temperatures, leading to a maximum nucleation rate at an intermediate temperature. The maximum is of greater magnitude and occurs at a higher temperature for Jhet.

Fig. 7
figure 7

(a) Rates for both homogeneous nucleation and heterogeneous nucleation of α phase as function of temperature; (b–f) α precipitation upon cooling from 950°C to 700°C at a rate of 5°C/s: (b) 860°C, (c) 855°C, (d) 770°C, (e) 765°C, (f) 740°C; (g) Color scheme for all 12 α variants (Color figure online)

Full size image

Nucleation first occurs heterogeneously at the prior β GB upon cooling (Fig. 7b). The variant selected for GB α maintains a Burgers orientation relationship (BOR) with β1, and the OR is described as \( [\bar{1}11]_{{\beta_{1} }} ||[\bar{1}\bar{1}20]_{\alpha } \) and \( (101)_{{\beta_{1} }} ||(0001)_{\alpha } \). Such a variant selection is made based on Refs. 39 and 40: the selected GB α maintains an OR with β2 (or non-Burgers grain) that has the smallest deviation from the BOR. In other words, the misorientation angle θm associated with such a deviation matrix (β∆JβBOR) is the smallest among all 24 θm, and θm ≤ 15°. The catalytic factor due to heterogenous nucleation is \( \Delta G_{\text{het}}^{*} /\Delta G_{\hom }^{*} , = 0.18 \).

Heterogenous nucleation occurs at t = 17.5 s (i.e., T = 862.5°C) with a maximum rate reached at t = 18.7 s (856.3°C), and ceases at t = 19.1 s (i.e., T = 854.5°C). During this period (1.6 s), a total number of 11 α precipitates nucleate heterogeneously at the GB. The corresponding microstructure evolution is shown Fig. 7b, c, and d. The introduced α nuclei take an initial shape of a spherical cap at the GB. As shown in Fig. 7b, two GB α at 860°C already grow and exhibit a typical Widmanstätten lath-like morphology, i.e., side plates are developing from the GB α. Upon further cooling from 860°C to 855°C, eight more α precipitates of the same variant nucleate heterogeneously at the GB and have grown to exhibit a lath-like morphology as well (Fig. 7c). The variation in the size (length of an α lath along the growing direction) scale of the α precipitate microstructure in Fig. 7c clearly indicates the occurrence of concurrent nucleation and growth of GB α. Upon further cooling to 770°C, the progressive growth of α side plates towards the grain interior results in the formation of a complete colony structure in the β1 grain, which consists of parallel α laths separated by β lamella, as shown in Fig. 7d. It is also observed that the lateral growth of the GB α along the grain boundary plane leads to formation of a continuous layer of α phase decorating the whole GB.

Upon further cooling from 770°C to 700°C, homogenous nucleation of α phase starts to occur in both prior β grains. It firstly occurs in β2 at t = 35.1 s (i.e., T = 774.5°C) with a maximum rate reached at t = 37.0 s (765°C), and completes at t = 39.7 s (i.e., T = 751.5°C). During this period (4.6 s), a total number of 391 α precipitates nucleate homogeneously in β2. In β1, α precipitation through homogeneous nucleation starts later at t = 36.1 s (i.e., T = 769.5°C) and completes at t = 43.7 s (i.e., T = 731.5°C). During this period (7.6 s), a total number of 36 α precipitates nucleate homogeneously in β1. The corresponding microstructure evolution is shown in Fig. 7d, e, and f.

As shown in Fig. 7d, at 770°C, α precipitates have nucleated homogeneously in the β2 with the nucleation sites apparently at a certain distance away from the grain boundary plane. This occurs because the growth of GB α rejects β stabilizing elements to the adjacent β matrix. Different from the GB α, for which a single variant is often observed, homogenously nucleated α precipitates may belong to multiple variants (see the color scheme for each α variant in Fig. 7g). With further cooling down to 765°C, more α precipitates nucleate homogeneously in the β2 grain, which occur during the growth of the early nucleated α precipitates, as shown in Fig. 7e. The concurrent nucleation of new α and growth of early formed α precipitates, of multiple variants, leads to a development of a basket-weave microstructure throughout the β2 grain interior upon cooling. Concurrently, α precipitates also nucleate homogeneously and grow in the β1, with the nucleation sites preferentially distributed within β lamellae in the colony structure. Spatial variation of α + β two-phase microstructure across the GB is clearly seen in Fig. 7f. The colony microstructure develops from the GB α layer in β1, while the basket-weave microstructure forms in β2.

Figure 8 demonstrates the variation of the resulting α precipitate microstructure in Ti-64 as a function of cooling rate. The cooling rate range considered was from 5°C/s to 20°C/s. As can be seen from Fig. 8a, b, and c, precipitate microstructures vary significantly with the cooling rate. In the β1 grain, a slow cooling rate generates a microstructure with large α colonies and coarsely spaced α lamellae (Fig. 8a). With increasing cooling rate, the development of a colony structure is interrupted by the basket-weave structure formed through homogenous nucleation in the untransformed β1 matrix (Fig. 8c). In β2 grain, even though the microstructure is predominantly of basket-weave type under the three different cooling rates considered, the size scale and number density of the constituent α laths are dramatically different, with the size and number density decreasing and increasing, respectively, with increasing cooling rate.

Fig. 8
figure 8

(a–c) Influence of cooling rate on the resulting α + β two-phase microstructure, (a) 5°C/s, (b) 10°C/s, and (c) 20°C/s; (d–f) Temporal evolution of the rates of homogeneous and heterogeneous nucleation of the α phase under different cooling rates

Full size image

Key microstructural features in the lamellar microstructure formed upon cooling include a continuous GB α layer, an α colony, and α lamellae (laths).41 Variations of these microstructure features with cooling rates are captured by the simulations. For example, the thickness of α laths and the size of an α colony (region inside which the α lamellae are parallel) increase with decreasing cooling rate. The spacing among α laths in the colony structure increases with decreasing cooling rate as well.

Variations of these key microstructure features with the cooling rate from the β phase region agree well with available experimental observations42 and can be explained by the interplay between homogeneous and heterogenous nucleation as a function of cooling rate. For each cooling rate, α precipitation occurs preferentially at the GB through heterogenous nucleation. Taking a cooling rate of 5°C/s as an example (Fig. 8d), the microstructure evolution is accompanied by nucleation starting from T = 870°C down to T = 850°C, which is referred to as the first peak of nucleation. This peak is followed by a period of time within which nucleation is completely shut down (no nucleation events occur). A new peak of nucleation starts at T = 780°C, reaching a maximum rate at T = 760°C, and continues down to 730°C. A small peak is also observed at T = 740°C. This indicates that the system exhibits three peaks of well-separated nucleation. While the first corresponds to heterogenous nucleation at the GB, the second and third result from homogenous nucleation in both adjacent β grains. During the interval between the first and second peaks, the microstructure evolves through growth of α laths developing from GB α, leading to the formation of a colony structure with the depletion of supersaturation in the adjacent β matrix. Upon further cooling, this supersaturation increases again, resulting in an increase of the driving force for nucleation to the point where homogenous nucleation occurs. During the third peak of nucleation, some smaller particles are introduced in both β grains. The trimodal size of α precipitates results from the three peaks of well-separated nucleation, with those bigger particles being formed during the first peak of nucleation (e.g., α laths within colony).

It becomes clear that the influence of the cooling rate on the interplay between homogeneous and heterogenous nucleation can be characterized using the number of nuclei generated within each peak, the time duration of each peak, and the time interval between different peaks, as shown in Fig. 8d, e, and f. Even though the onset temperature of each peak looks similar and the maximum of each peak appears at a similar temperature as well, the number of nuclei generated within each peak increases dramatically with increasing cooling rate due to a rapid increase in the chemical driving force for nucleation. The time duration of each peak and the time interval between them decrease with increasing cooling rate. As a result, the size difference between the larger α laths and the smaller ones in the β2 grain is less significant as compared with that in the case of a cooling rate of 5°C/s, because shorter growth times are available for the growth of the precipitates with increasing number density associated at the fast cooling rate. Comparing the microstructures shown in Fig. 8a, b, and c, there is a clear tendency for the particle density to increase and the overall particle size to decrease with increasing cooling rate.

It is also evident that α + β microstructure formation upon cooling from the β phase region is complex, not only because it involves features spanning a wide range of length scales, but also because those features are interdependent due to the interplay between heterogenous nucleation at GB and homogeneous nucleation within the grain interior, which is strongly dependent on cooling rate.

Note that cooling rates slower than 20°C/s result in the Widmanstätten structure, while rates larger than 410°C/s lead to a fully martensitic microstructure.7 In view of the current standard LPBF practice, which is conducted at powder bed temperatures below the α′ martensitic transformation temperature (Ms, 575°C7), and the high cooling rates (e.g., up to ~ 6000°C/s) experienced by the solidified metal close to the melt pool, the resulting microstructure often features columnar prior-β grains filled with acicular α′ martensite.3,9 In particular, the successive layers exert a cyclic thermal influence leading to in situ decomposition of a near α′ martensitic structure or precipitation of the equilibrium α precipitate. Simulation of the precipitation reaction of α′ phase in a representative prior β polycrystalline structure (formed during solidification provided by the CA simulation) subjected to complex thermal cycles (including multiple heating/cooling cycles) is currently underway.

Computed Elastic Responses of AM Ti-64 Microstructures

We first examine the microscopic elastic responses of the microstructure to applied strain by examining the resulting von Mises equivalent stress (σv) fields, defined as

$$ \sigma_{\text{v}} = \sqrt {(1/2)[(\sigma_{11} - \sigma_{22} )^{2} + (\sigma_{22} - \sigma_{33} )^{2} + (\sigma_{33} - \sigma_{11} )^{2} ] + 3[\sigma_{12}^{2} + \sigma_{23}^{2} + \sigma_{31}^{2} ]} $$
(9)

where σij (i, j = 1–3) is the stress tensor obtained from Eq. 8. Figure 9a and b show the computed σv profiles under the applied strain \( \varepsilon_{11}^{\text{appl}} \sim 1.75\% \) for two (α + β)microstructures formed at cooling rates of 5°C/s and 20°C/s, respectively. Note that local stress is more concentrated at specific α precipitaates. To explicitly show the difference in the mechanical response, we define the stress hotspots using a simple criterion: σv ≥ σY, where σY is the yield strength. We choose σY = 1.0 GPa for Ti-64 in this study.43 Note that this criterion does not necessarily predict and/or determine the local yield points. Instead, we evaluate and compare the microstructures in terms of the propensity for mechanical failure. Figure 9c and d shows the spatial distribution of the identified stress hotspots (see the red regions in the figures) for two given microstructures. It is found that, under the same loading condition, the total volume fraction of hotspots in the microstructure for the cooling rate of 5°C/s is higher than that in the microstructure for the cooling rate of 20°C/s, while the hotspots for 20°C/s are more finely and uniformly distributed than those for 5°C/s. To better quantify the microstructure-dependent mechanical responses, we also monitor the evolving volume fractions of stress hotspots with increasing strain applied to microstructures formed at three different cooling rates, as shown in Fig. 9e. Even though the onset of the stress hotspots occurs at \( \varepsilon_{11}^{\text{appl}} \sim 1.75\% \) for all three different microstructures considered, the one for 5°C/s exhibits stronger susceptibility to the formation of hotspots than the other two microstructures under the same applied strain. This clearly demonstrates the differences in microscopic elastic responses to the applied loads among the (α + β) microstructures resulting from different thermal histories.

Fig. 9
figure 9

Microstructure-based elastic response calculations: Computed von Mises stress profiles σv in Ti-64 two-phase microstructures under \( \epsilon_{11}^{\text{appl}} \) for cooling rates of (a) 5°C/s and (b) 20°C/s; Spatial distribution of the identified stress hotspots (i.e., σv > yield strength) for the microstructures formed at the cooling rates of (c) 5°C/s and (d) 20°C/s, and (e) evolution of hotspot volume fractions (fHS) with increasing \( \epsilon_{11}^{\text{appl}} \) (Color figure online)

Full size image

Our computational approach is also employed to extract the effective elastic moduli of α + β microstructures as explained above. The computed effective elastic moduli for three different microstructures are presented in Supplementary Table 1, which indicates that the effective elastic properties also depend on the phase microstructural features. Note that the computed effective elastic moduli can serve as inputs for part-scale mechanical modeling (e.g., effective medium modeling44).

We emphasize that the results of micro- and mesoscopic elastic responses demonstrate the importance of the microstructure generated by solid-state phase transformation, which may play an important role in determining the deformation mechanisms and mechanical behaviors of additively manufactured titanium components. However, several assumptions made in the current study and limitations of the elastic response calculations need to be noted. First, the elastic moduli of the individual α and β phases used in calculations are temperature independent. Second, the mechanical response of microstructures under a given applied strain is assumed to be within the elastic deformation regime, without accounting for any possible plastic deformation. Third, the (α + β) two-phase microstructures considered in the current study are formed upon cooling down to a temperature (700°C) above the martensite starting temperature and at a relatively slow cooling rate (≤ 20°C/s). Therefore, the elastic response of the martensitic phase (α′) that would form at relatively faster cooling rates is not addressed in this study.

Conclusion

By formulating an integrated simulation framework, we simulate the microstructure evolution in Ti-6Al-4V (Ti-64) during a single-track laser powder bed fusion (LPBF) process and investigate its correlation with processing variables:

  1. 1.

    The temporal evolution and spatial distribution of the three-dimensional temperature field, melt pool geometry, and resulting grain structure and solidification morphology are simulated during a single-layer LPBF process of Ti-64 by using an integrated powder-scale ALE3D heat transfer and fluid flow model and mesoscale cellular automaton model;

  2. 2.

    The variation of the melt pool geometry, grain growth direction and morphology with processing parameters (i.e., laser power and scanning speed) agrees well with available experimental data. An increase of the scanning speed results in the development of grains mainly oriented in a direction normal to the scanning direction.

  3. 3.

    During subsequent solid-state phase transformation upon cooling, concurrent nucleation, growth, and coarsening of the equilibrium α phase in a bicrystalline β matrix is simulated by the integrated quantitative phase-field model and the explicit nucleation algorithm, with their inputs linked directly with thermodynamic and atomic mobility databases.

  4. 4.

    The key precipitate microstructure features such as number density and spatial uniformity are determined by the interplay between homogeneous nucleation in the grain interior and heterogeneous nucleation at a prior grain boundary. Their variations with cooling rate agree well with available experimental observations.

  5. 5.

    Micro- and mesoscopic elastic response calculations for Ti-64 microstructures under different cooling rates explicitly show the impacts of the solid-state phase microstructures on the mechanical responses to the applied loads.

The maturation of metal AM away from rapid prototyping to meet its end goal of rapid manufacturing of high-quality parts calls for a fundamental understanding of the interplay of physics at different time and length scales, ranging from the laser–powder interaction, to the melt pool dynamics, thermal history, microstructure, and resulting mechanical properties. The modeling framework developed herein is successfully applied to a single track, but its validity extends to the full AM build process.