Pareto optimality and robustness in bi-blending problems

Abstract

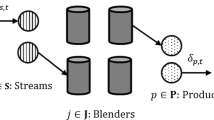
The mixture design problem for two products concerns finding simultaneously two recipes of a blending problem with linear, quadratic and semi-continuity constraints. A solution of the blending problem minimizes a linear cost objective and an integer valued objective that keeps track of the number of raw materials that are used by the two recipes, i.e. this is a bi-objective problem. Additionally, the solution must be robust. We focus on possible solution approaches that provide a guarantee to solve bi-blending problems with a certain accuracy, where two products are using (partly) the same scarce raw materials. The bi-blending problem is described, and a search strategy based on Branch-and-Bound is analysed. Specific tests are developed for the bi-blending aspect of the problem. The whole is illustrated numerically.

Appendices

Appendix 1: Products

• RumCoke

Dimension = 3; Raw materials involved = {RM1,RM2,RM4};

Raw material cost = (0.1,0.7,4.0);

Linear constraints:

h ₁(x)=−1.5x ₁+0.5x ₂−0.5x ₃≥0.0,

h ₂(x)=0.3x ₁−0.5x ₂−0.3x ₃≥0.0;

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0;\ i=1,2 )$.

• Case2

Dimension = 3; Raw materials involved = {RM1,RM2,RM3};

Raw material cost = (0.1,0.7,1.0);

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0,\ i=3,\ldots,7 )$.

• Case3

Dimension = 3; Raw materials involved = {RM1,RM2,RM4};

Raw material cost = (0.1,0.7,4.0);

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0,\ i=7,\ldots, 10 )$.

• Case4

Dimension = 3; Raw materials involved = {RM2,RM3,RM4};

Raw material cost = (0.7,1.0,4.0);

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0,\ i=2,7,9,11 )$.

• UniSpec1-5

Dimension = 5; Raw materials involved = {RM5,RM6,RM7,RM8,RM9};

Raw material cost = (114,115,107,127,115);

Linear constraint:

h ₃(x)=0.1493x ₁+0.6927x ₂+0.4643x ₃+0.7975x ₄+0.5967x ₅≥0.35;

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0,\ i=12,\ldots,14 )$.

• UniSpec5b-5

Dimension = 5; Raw materials involved = {RM5,RM6,RM7,RM8,RM9};

Raw material cost = (114,115,107,127,115);

Quadratic constraints $(g_{i}(x)=x^{T}A_{i} x + b^{T}_{i} x + d_{i} \leq0,\ i=15,\ldots,18 )$.

• Quadratic constraints

A ₁[3×3]=(0,−16,0,−16,0,0,0,0,0);

b ₁[3×1]=(8,8,0);d ₁=−1

A ₂[3×3]=(10,0,2,0,0,0,2,0,2);

b ₂[3×1]=(−12,0,−4);d ₂=3.7

A ₃[3×3]=(0.001,−0.001,0.0085,−0.001,0.008,−0.0105,0.0085,−0.0105,−0.021)

b ₃[3×1]=(−0.0145,−0.0205,0.073); d ₃=−0.0165

A ₄[3×3]=(−0.004,0.0005,0.002,0.0005,−0.001,−0.003,0.002,−0.003, 0.014)

b ₄[3×1]=(0.0155,0.0515,−0.121); d ₄=−0.006

A ₅[3×3]=(20.605,−5.087,−10.9885,−5.087,32.003,−43.476,−10.9885, −43.476, −81.278)

b ₅[3×1]=(0.1995,−0.097,126.7685); d ₅=−20.5063

A ₆[3×3]=(0.766,−0.1205,2.4735,−0.1205,0.528,1.9835,2.4735,1.9835,−7.822)

b ₆[3×1]=(−2.432,−15.191,10.712); d ₆=3.21125

A ₇[3×3]=(116.75,−3.09,168.553,−3.09,−67.424,515.114,168.553,515.114,−845.215)

b ₇[3×1]=(−287.43,−645.926,354.537); d ₇=115.0953

A ₈[3×3]=(1.0,3.0,−0.5,3.0,−5.0,−3.5,−0.5,−3.5,−2.0)

b ₈[3×1]=(0.832,0.832,0.832); d ₈=0.968

A ₉[3×3]=(2.0,−1.5,1.0,−1.5,1.0,−1.0,1.0,−1.0,3.0)

b ₉[3×1]=(0.12,0.12,0.12); d ₉=−1.60

A ₁₀[3×3]=(4.0,−1.5,−1.5,−1.5,4.0,−2.5,−1.5,−2.5,4.0)

b ₁₀[3×1]=(−0.026,−0.026,−0.026); d ₁₀=−2.141

A ₁₁[3×3]=(4.0,−1.0,−2.0,−1.0,5.0,−3.0,−2.0,−3.0,4.0)

b ₁₁[3×1]=(−0.019,−0.019,−0.019); d ₁₁=−2.631

A ₁₂[5×5]=(−1.473, 8.215, −27.204, 46.119, 2.059, −11.929, −12.768, 8.215, 37.733346, 5.127, 95.691, 34.954, 20.165, 19.445, −27.204, 5.127, −21.743, 36.843, −7.126, 4.029, −4.152, 46.119, 95.691, 36.843, 189.643, 93.359, 52.904, 54.802, 2.059, 34.954, −7.126, 93.356, 31.885, 7.528, 10.248, −11.929, 20.165, 4.029, 52.904, 7.528, 11.951, 10.964, −12.768, 19.445, −4.152, 54.802, 10.248, 10.964, 7.197)

b ₁₂[5×1]=(4.5675, 34.7289, 70.5707, −82.2761, 29.3169); d ₁₂=−35

A ₁₃[5×5]=(1.35, −4.41, 17.60, −92.45, 2.74, −29.94, −14.05, −4.41, −39.13, −6.11, −126.38, −29.81, −63.42, −43.97, 17.60, −6.11, 15.45, −76.60, 5.93, −44.05, −20.54, −92.45, −126.38, −76.60, −240.64, −117.46, −125.18, −114.98, 2.74, −29.81, 5.93, −117.46, −22.90, −47.37, −30.68, −29.94, −63.42, −44.05, −125.18, −47.37, −73.39, −73.99, −14.05, −43.97, −20.54, −114.98, −30.68, −73.99, −55.33)

b ₁₃[5×1]=(−2.1232, −9.0403, −42.2072, 190.5292, −9.9529); d ₁₃=10

A ₁₄[5×5]=(−0.670, 4.284, −12.837,23.708, 1.677, −8.964, −4.859, 4.284, 21.380, −1.188, 28.990, 13.216, 17.177, 16.620, −12.837, −1.189, −21.376, 9.841, −7.298, −10.043, −8.981, 23.708, 28.990, 9.841, 49.385, 25.574, 15.561, 21.666, 1.677, 13.216, −7.298, 25.574, 8.419, 4.149, 6.595, −8.965, 17.177, −10.043, 15.561, 4.149, 1.090, 6.292, −4.859, 16.620, −8.981, 21.666, 6.594, 6.292, 5.906)

b ₁₄[5×1]=(0.7097, −13.0982, 27.5078, −49.1608, −7.3725); d ₁₄=−2

A ₁₅=−A ₁₂; b ₁₅=−b ₁₂; d ₁₅=45

A ₁₆=−A ₁₃; b ₁₆=−b ₁₃; d ₁₆=−21

A ₁₇[5×5]=(0.0, −11.556, −1.114, 14.690, −11.411, 0.121, −0.150, −11.556, −3.316, −2.116, 7.313, −8.800, 19.897, 9.051, −1.114, −2.116, 4.728, 16.250, −4.535, 18.319, 11.537, 14.690, 7.313, 16.250, 40.428, 9.766, 21.512, 15.266, −11.412, −8.800, −4.535, 9.766, −10.165, 10.088, 1.889, 0.121,19.897, 18.319, 21.511, 10.088, 28.569, 27.239, −0.150,9.051, 11.537, 15.266, 1.889, 27.239, 19.965)

b ₁₇[5×1]=(1.7278, 23.5166, 5.6724, −32.0798, 19.0154); d ₁₇=−5

A ₁₈=A ₁₄; b ₁₈=b ₁₄; d ₁₈=−1

Appendix 2: Linear and quadratic feasibility

• Linear infeasibility

If for one of the linear constraints h _i (x)≤0 all vertices are infeasible (h _i (v _k,s )>0, s=1,…,t _k ), then C _k does not fulfil h _i (x)≤0.

• Quadratic infeasibility

Given a simplex C _k ∈Λ _j and the set of quadratic constraints {g _i (x)≤0, i=1,…,m _j }, C _k can be rejected if ∀x∈C _k ∃ i:g _i (x)>0.

Around each vertex v _k,s , s=1,…,t _k , a so-called infeasibility sphere B _k,s is defined:

B _k,s cannot contain a feasible point. Different ways of calculating values of radii ρ _k,s are described in Casado et al. (2007).

If none of the vertices of C _k is feasible, the spheres can be used to prove that C _k cannot contain a feasible quadratic solution. The following tests to prove the infeasibility of simplex C _k are used by the following Algorithm 1:

SCTest:

(Single Cover Test). One of the spheres B _k,s with radius ρ _k,s , s=1,…,t _k , covers the simplex completely, i.e. C _k is proved infeasible if there exists a vertex v _k,s such that ρ _k,s >max _z ∥v _k,s −v _k,z ∥, z≠s, z=1,…,t _k .

MCTest:

(Multiple Cover Test). A simplex C _k which is not covered by a single sphere B _k,s can still be covered by $\bigcup_{s=1}^{t_{k}} B_{k,s}$. In Casado et al. (2007), it is proven that if a mixture x∈C _k is covered by all spheres, i.e. $x \in\bigcap_{s=1}^{t_{k}}B_{k,s}$, then $C_{k} \subset\bigcup_{s=1}^{t_{k}} B_{k,s}$. This means that all the possible mixtures in C _k are covered by at least one sphere B _k,s , and consequently C _k is infeasible.

PCTest:

If the SCTest and MCTest fail, Algorithm 1 focuses on the infeasibility sphere centred at a generated interior point. If it is shown to be infeasible for at least one of the constraints, a new infeasibility sphere is generated. The advantage of using an interior point is that its distance to the farthest vertex is smaller than the largest distance in between two vertices of the simplex.

• ε-Infeasibility

The ε-robustness requirement gives the opportunity to reject a simplex C _k that is close enough to an infeasible solution. A simplex C _k with an infeasible point x such that max _s ∥x−v _k,s ∥<ε cannot contain an ε-robust solution.