Phase Diagram for the System RuO₂-TiO₂ in Air

Abstract

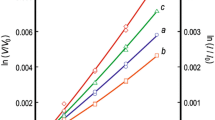
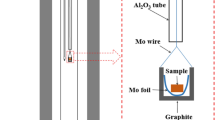
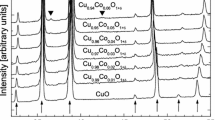
There are conflicting reports in the literature regarding solid solubility in the system RuO₂-TiO₂. To resolve this issue a few experiments were conducted in air at 1673, 1723, and 1773 K. The results show limited terminal solid solubility. There is an extended solid-state miscibility gap that intersects the decomposition curve for the RuO₂-rich solid solution generating a peritectoid reaction at 1698 K. The measured equilibrium compositions of the solid solutions are used to develop a thermodynamic description of the oxide solid solution with rutile structure. Using the subregular solution model, the enthalpy of mixing can be represented by the expression, $\Delta H^{\rm M} /{\text{J}} \cdot {\text{mol}}^{{ - 1}} = X_{{{\text{TiO}}_{2} }} X_{{{\text{RuO}}_{2} }} {\left( {34,100X_{{{\text{TiO}}_{2} }} + 30,750X_{{{\text{RuO}}_{2} }} } \right)}$. The binodal and spinodal curves and T-X phase diagram in air are computed using this datum and Gibbs energy of formation of RuO₂ available in the literature. The computed results suggest that equilibrium was not attained during solubility measurements at lower temperatures reported in the literature.