1 Introduction

Aluminum, magnesium, and their alloys are widely used as lightweight materials in various industrial applications. In particular, magnesium has attracted much attention because it is the lightest practical metal. However, magnesium exhibits inferior plastic processing and anti-corrosive behavior compared to aluminum. To compensate for the demerits inherent to both metals, production of porous aluminum is desirable. The strength of conventional porous aluminum with isotropic spherical pores is quite low due to the stress concentration occurring around the pores and the poor mechanical strength limits the applications of conventional porous aluminum.[1] On the other hand, porous metals with slender cylindrical pores aligned in one direction (lotus-type[2] (hereafter lotus metals) and gasar[3] porous metals) do not significantly contribute to stress in the slender pore growth direction. Consequently, the mechanical strengths of lotus and gasar metals are higher than those of conventional porous metals. Therefore, lotus aluminum possessing slender directional pores aligned in one direction is one of the most promising candidates for lightweight structural materials.[4] Numerous investigations have focused on the fabrication of porous aluminum and its alloys with slender directional pores formed by unidirectional solidification in a hydrogen atmosphere. Particularly, solidification defects have been emphasized for basic and applied research of a lightweight material. Table I is a compilation of these works.[5–15] Although aluminum alloys have high porosities, especially alloys with Si[15] and Fe,[12] none of the previous works produced porous aluminum with directional pores and a high porosity; the porosity is limited to 5 pct at most.

Table I Previously Reported Porosity and Pore Size Results in Porous Aluminum and Its Alloys with Directional Pores Fabricated in a Hydrogen Atmosphere
Full size table

Lotus aluminum can be fabricated utilizing the hydrogen solubility gap between a liquid and solid at the melting point in the unidirectional solidification process in a hydrogen atmosphere. When the melt dissolving hydrogen is solidified, the insoluble hydrogen is precipitated to evolve directional pores in the solidified region at the solid/liquid interface. Therefore, the following conditions are critical to fabricate highly porous lotus metals.

  1. (1)

    The hydrogen concentration dissolved in the molten metal should exceed several at. pct.

  2. (2)

    The metal should hold a smaller solid solubility of hydrogen so that the solubility gap between liquid and solid metals becomes larger.

The system of hydrogen with copper, magnesium, and several transition metals such as iron, nickel, cobalt, and chromium can satisfy these conditions, and produce highly porous lotus metals.[4] However, the hydrogen solubility in liquid and solid aluminum[16] is only about 2 pct of those for magnesium, copper, and transition metals.[17,18] Consequently, previous researchers considered the fabrication of highly porous lotus aluminum difficult; none of the previous reports successfully fabricated lotus aluminum with a porosity above 5 pct.

On the other hand, extensive research on porous aluminum with directional pores has been conducted considering pores to be defects.[5,6,8–12,14] The formation of pores during aluminum solidification is a major drawback because porousness is detrimental to the mechanical properties, and reduces both fatigue performance and total elongation. Experimental studies on the formation of pores during solidification of aluminum alloys have classically correlated the final pore structure with the solidification processing parameters such as the initial hydrogen solubility, solidification velocity, etc.[11] The two main causes of porosity are hydrogen and inadequate feeding to compensate for the volumetric shrinkage upon solidification. When a process is kinetically complicated, distinguishing between the relative importance of these two factors is difficult. However, a few in situ observations of pore formation during aluminum solidification have clarified that pore growth during the initial stage is primarily controlled by a hydrogen diffusion mechanism, while growth in the second stage, is controlled by volume shrinkage.[11]

The morphology of the growth of lamellar and rod eutectics in duel phased alloys is affected by the solidification conditions such as solute concentration, solidification velocity, temperature gradient in the solidification front (hereafter referred to as the temperature gradient), molten temperature, etc.[19,20] Consequently, solute diffusion controls the morphology of both the microstructure and the porous structure. Thus, to increase porosity and to clarify the pore formation mechanism in lotus aluminum, it is reasonable to consider the competitive growth between directional pores and solid metal because the hydrogen flux is related to the solidification conditions.

Several experimental investigations have examined the effects of partial pressure and solidification velocity on the porosity and pore size in metals (copper,[15,21] stainless steel,[22] and magnesium[23]) to evaluate the porosity and pore size from the solidification processing parameters. On the other hand, pore growth in lotus metals has been theoretically evaluated from the viewpoint of competitive growth between directional pores and solid metal. Based on the mass balance between insoluble hydrogen due to the solubility gap and formed pores corresponding hydrogen, Yamamura et al.[21] and Liu et al.[23] have theoretically investigated the porosity of lotus metals as a function of hydrogen solubility, which depends on the partial gas pressure and molten temperature. The calculated porosities with the appropriate fitting parameters agree well with the experimental results. However, the conclusive formula to calculate porosity depends on only the initial hydrogen concentration between the liquid and solid phases, and is independent of the solidification conditions. On the other hand, Drenchev et al.[24] have proposed a comprehensive model for pore formation in lotus copper using classical nucleation theory; they analyzed the diffusion boundary layer ahead of the solid/liquid interface with respect to the diffusion process and structure formation. The calculated porosities and pore diameters did not agree with the experimental results because heterogeneous nucleation modeling of the pores was insufficient.

In the present work, the influence of solidification conditions (solidification velocity, hydrogen partial pressure, temperature gradient, and melt temperature) on pore formation of lotus aluminum is experimentally and theoretically investigated to elucidate the pore formation mechanism as well as to control porosity. We fabricated lotus aluminum with slender unidirectional pores using a continuous casting technique under controlled solidification conditions. In particular, the present work clarifies that the porosity and the pore size are affected significantly by the solidification velocity, which is decreased by one to two orders of magnitude compared to those for copper, magnesium, and transition metals. Based on this knowledge, lotus aluminum with a porosity as high as 40 pct is obtained for the first time.

2 Experimental Procedure

A continuous casting technique was utilized for unidirectional solidification in a pressurized hydrogen atmosphere under controlled solidification conditions. Figure 1(a) schematically illustrates the continuous casting apparatus. The apparatus consisted of three parts: an upper part to melt the metal and dissolve hydrogen, a middle part to solidify the melt, and a lower part to mechanically transfer the solidified rod or slab.[15] Pure aluminum (purity 99.99 pct) was melted by inductive heating in a crucible, and molten aluminum was held for 600 seconds at a given melt temperature to ensure a uniform distribution of dissolved hydrogen in the melt. The temperature of the melt in the crucible was measured using two WRe 5/26-type thermocouples located 5 mm from the bottom of the crucible. Then to solidify the melt continuously in a downward direction, a graphite dummy bar pulled molten aluminum through a cooling mold at a constant solidification velocity.

Fig. 1
figure 1

(a) Schematic drawings of the continuous casting apparatus and (b) temperature measurement of the solidification front near the dummy bar

Full size image

Figure 1(b) shows the setup to measure the solidification temperature using two K-type thermocouples inserted in the graphite dummy bar. To ensure the temperature gradient was at a steady state, the temperature was measured 20 mm above the top of the dummy bar. The measured temperature was recorded every second using a temperature recorder (Keyence Co., Ltd.; GR-3500). The temperature gradient was calculated using the obtained cooling curve in the temperature range from 933 K to 873 K (660 °C to 600 °C) (temperature-time curve). The temperature gradient was determined using the following equation:

$$ G = \frac{V}{R} $$
(1)

where G, V, and R are the temperature gradient (K/mm), cooling rate during unidirectional solidification (K/s), and solidification velocity [mm/s], respectively. The temperature gradient was determined from the average of two temperature gradients, whose difference was less than 0.3 K/mm.

The effects of different characteristics on pore morphology were examined. The influence of the solidification rate was probed by melting pure aluminum and unidirectionally solidifying in a mixture of hydrogen 0.25 MPa and argon 0.25 MPa with a constant temperature gradient and melt temperature of 9.7 K/mm and 1223 K (950 °C), respectively, while changing the solidification velocity from 0.5 to 0.9 mm/minute. The impact of hydrogen partial pressure was investigated by melting aluminum and unidirectionally solidifying in three different atmospheres: hydrogen 0.5 MPa, argon 0.5 MPa, or mixed gas (0.5 MPa) consisting of hydrogen (0.25 MPa) and argon (0.25 MPa) when the solidification velocity, temperature gradient, and melt temperature were set to 0.9 mm/minute, 9.5 K/mm and 1223 K (950 °C), respectively.

Additionally, the impact of the temperature gradient on pore morphology was probed by changing the temperature gradient while melting pure aluminum and unidirectionally solidifying in a mixed atmosphere of hydrogen (0.5 MPa) and argon (0.5 MPa). The temperature gradient was controlled by adjusting the contact area between the mold and cooling block; the contact area with the cooling block was decreased by introducing a groove on the contact surface of the mold, suppressing the temperature gradient. The temperature gradients were set to 7.2, 9.1, 10.1, or 14.5 K/mm. The solidification velocity and molten temperature were maintained at 0.5 mm/minute and 1373 K (1100 °C), respectively.

The influence of melt temperature on pore morphology was examined by melting pure aluminum in a 0.5 MPa hydrogen atmosphere. The melt temperatures were changed in the range from 1173 K to 1273 K (900 °C to 1000 °C). Because the melt temperature significantly influenced the temperature gradient, a constant temperature gradient of 9.5 ± 0.5 K/mm was achieved by changing the contact area between the mold face and the cooling block face. On the other hand, the solidification velocity was kept constant at 0.9 mm/minute.

The solidified aluminum ingot slabs were cut with a spark-erosion wire cutting machine (AQ325L, Sodik Corp., Yokohama, Japan) either parallel or perpendicular to the solidification direction. An optical microscope (Digital HD Microscope, VHX-200, Keyence Corp.) and a scanning electron microscope (SEM; JSM-6360T, JEOL Corp., Tokyo, Japan) were used for cross-sectional observations, while an image analyzer (WinRoof, Mitani Corp., Fukui, Japan) was used to obtain the porosity and pore diameter.

3 Experimental Results

Figure 2 shows the typical pore morphology perpendicular (upper row) and parallel (lower row) to the solidification direction of lotus aluminum as a function of solidification velocity from 0.5 to 0.9 mm/minute. Lotus aluminum was fabricated by unidirectional solidification in a mixture of hydrogen (0.25 MPa) and argon (0.25 MPa). Figure 2(f) shows an outer view of lotus aluminum with the highest porosity of nearly 40 pct. Unidirectional pores aligned parallel to the solidification direction are observed in the solidified lotus aluminum. Figure 3 shows the influence of solidification velocity on the porosity and average pore diameter in lotus aluminum fabricated in the same manner as that shown in Figure 2. The porosity and average pore diameter decrease as the solidification velocity increases.

Fig. 2
figure 2

Cross-sections perpendicular (upper row) and parallel (lower row) to the solidification direction of lotus aluminum. Solidification velocity: (a) 0.5 mm/minute, (b) 0.6 mm/minute, (c) 0.7 mm/minute, (d) 0.8 mm/minute, and (e) 0.9 mm/minute. (f) Outer view of lotus aluminum with the highest porosity of nearly 40 pct

Full size image
Fig. 3
figure 3

Porosity and pore diameter versus solidification velocity of lotus aluminum fabricated in a mixture of hydrogen (0.25 MPa) and argon (0.25 MPa). Temperature gradient and melt temperature are 9.7 K/mm and 1223 K (950 °C), respectively

Full size image

Figure 4 shows the pore morphology in lotus aluminum fabricated by unidirectional solidification at a solidification velocity of 0.9 mm/minute as a function of the hydrogen partial pressure; photos in the upper and lower rows are the cross-sectional views perpendicular and parallel to the solidification direction, respectively. The atmospheric total pressure was kept constant at 0.5 MPa, while the partial pressure of hydrogen was either 0, 0.25, or 0.5 MPa and the partial pressure of argon was 0.5, 0.25, or 0 MPa, respectively. The ingot solidified in an argon atmosphere does not exhibit pores (Figure 4(a)). In contrast, ingots prepared in a hydrogen atmosphere contain pores (Figures 4(b) and (c)). It is apparent that dissolving gas in the melt is responsible for the evolution of pores, because hydrogen but not argon can dissolve in molten aluminum. Figure 5 shows the dependence of porosity and pore diameter on the partial pressure of hydrogen in the mixture gas at a pressure of 0.5 MPa. Porosity and pore diameter increase as the hydrogen partial pressure increases.

Fig. 4
figure 4

Cross-sections perpendicular (upper row) and parallel (lower row) to the solidification direction of lotus aluminum fabricated in different atmospheres: (a) argon (0.5 MPa), (b) mixed gas of hydrogen (0.25 MPa) and argon (0.25 MPa), and (c) hydrogen (0.5 MPa). Temperature gradient and melt temperature are 9.5 K/mm and 1223 K (950 °C), respectively

Full size image
Fig. 5
figure 5

Dependence of porosity and pore diameter on hydrogen partial pressure. Lotus aluminum fabrication conditions are the same as those in Fig. 4

Full size image

Figure 6 shows cross-sectional views of the pore morphology perpendicular and parallel to the solidification direction of lotus aluminum fabricated at different temperature gradients. Figure 7 shows the dependence of porosity and average pore diameter of lotus aluminum fabricated in a mixed gas containing hydrogen (0.5 MPa) and argon (0.5 MPa) on the temperature gradient at a melting temperature of 1373 K (1100 °C) and a fixed solidification velocity of 0.5 mm/minute. The porosity and average pore diameter decrease as the temperature gradient increases. Figure 8 shows the change in pore morphology due to the difference in the melt temperature of lotus aluminum fabricated with a solidification velocity of 0.9 mm/minute in a 0.5 MPa hydrogen atmosphere. Figure 9 shows the dependence of porosity and pore diameter of lotus aluminum on the melt temperature. The porosity and average pore diameter increase as the melt temperature increases.

Fig. 6
figure 6

Cross-sections perpendicular (upper row) and parallel (lower row) to the solidification direction of lotus aluminum fabricated with different temperature gradients at the solid/liquid interface. Lotus aluminum is fabricated in a mixed gas of hydrogen (0.5 MPa) and argon (0.5 MPa) at a melt temperature of 1373 K (1100 °C) and a fixed solidification velocity of 0.5 mm/minute

Full size image
Fig. 7
figure 7

Dependence of porosity and pore diameter on temperature gradient. Lotus aluminum fabrication conditions are the same as those in Fig. 6

Full size image
Fig. 8
figure 8

Dependence of porosity and pore diameter on melt temperature of lotus aluminum fabricated with solidification velocity of 0.9 mm/minute in 0.5 MPa hydrogen. Temperature gradient is 9.5 ± 0.5 K/mm

Full size image
Fig. 9
figure 9

Comparison between the calculated porosity values and the experimental data from the temperature gradient effect on porosity of lotus aluminum. Porosity is evaluated in terms of Yamamura’s model by fitting the calculated value to the experimental result of porosity at a temperature gradient of 7.2 K/mm

Full size image

4 Discussion

Lotus aluminum can be fabricated via unidirectional solidification in a hydrogen atmosphere. Although hydrogen has a low solubility in aluminum, this work demonstrates that a porosity as high as 30 pct can be realized via a unidirectional solidification with a slow solidification velocity. Typically, the porosity and pore size are the parameters used to characterize pore morphology of lotus metals. On the other hand, solidification conditions are characterized by processing parameters, including solidification velocity, atmospheric hydrogen pressure, temperature gradient, melt temperature, etc. The porosity and pore diameter of lotus aluminum depend on the solidification velocity, hydrogen partial pressure, temperature gradient, and melt temperature. Below we discuss the influence of each processing parameter on the morphology parameters (the porosity and pore size) in lotus aluminum.

4.1 Effect of Hydrogen Partial Pressure on Porosity and Pore Size

The porosity and pore size increase as the hydrogen partial pressure increases (Figure 5). The dependence of porosity on hydrogen partial pressure has the same tendencies as those reported for lotus copper[21] and lotus stainless steel.[22] The effect of hydrogen pressure on the porosity can be explained in terms of Sieverts’ law because the experimental results show that the porosity is approximately proportional to the square root of the hydrogen partial pressure.

On the other hand, considering the increase in pore size due to the increase in hydrogen partial pressure, it is surmised that insoluble hydrogen is rejected at the solid/liquid interface when the aluminum melt solidifies, and this rejected hydrogen accumulates in the liquid. Hydrogen then inspissates, enhancing pore growth near the solid/liquid interface.

4.2 Effect of Solidification Velocity on Porosity and Pore Size

The present work demonstrates that both porosity and pore size in lotus aluminum decrease as the solidification velocity increases (Figure 3). Park et al. have investigated the effect of the solidification velocity on the porosity and pore size in lotus copper fabricated by a continuous casting technique.[25] They found that the pore size decreases as the solidification velocity increases, but the porosity is nearly independent of the solidification velocity. Park et al. have suggested that when the solidification velocity increases, the number of pore nucleation sites increases due to an increase in the degree of supercooling, and consequently, the average pore diameter decreases.[25] Similarly, the decrease in pore size in lotus aluminum can be also explained by supercooling.

However, supercooling cannot explain the decrease in porosity. The pores, which are considered to nucleate heterogeneously,[26] are grown by hydrogen diffusion of the insoluble hydrogen rejected at the solid/liquid interface. The amount of hydrogen diffusing from the liquid and solid into the pores increases as the solidification velocity decreases because long distance diffusion occurs more significantly. This is the reason why the porosity increases with decreasing solidification velocity.

4.3 Effect of Temperature Gradient on Porosity and Pore Size

To date, the lotus metal fabrication while controlling the temperature gradient near the solid/liquid interface has not been systematically investigated during directional solidification. However, one study has observed the difference in the pore morphology with and without a blower (existent or nonexistent cooling) during directional solidification using continuous zone melting. Ikeda et al.[22] fabricated lotus stainless steel, and found that the porosity and pore size increase as the temperature gradient decreases without a blower. Their finding is qualitatively consistent with the present result described in Figure 7.

According to Yamamura et al.’s model[21] (hereafter Yamamura’s model), the porosity was evaluated by considering the influence of the temperature gradient on hydrogen solubility and the resultant change on the pore volume in lotus copper. Because the soluble hydrogen content in solidified copper decreases with decreasing temperature, more hydrogen is evolved, increasing the porosity at lower temperatures. It is considered that the steeper the temperature gradient, the larger the porosity is. On the other hand, Boyle-Charles law predicts that the pore volume decreases as the temperature decreases. Thus, as the temperature gradient increases the volume of pores decreases, thereby decreasing the porosity.

Here, we discuss how the temperature gradient affects the porosity. However, the model calculation for lotus copper by Yamamura et al. cannot be applied as originally designed to lotus aluminum because the solubility difference between liquid and solid aluminum is much smaller than that in copper. Hence, to apply Yamamura’s model to lotus aluminum, the porosity was evaluated by fitting a variable parameter a, which is the ratio of the amount of escaped hydrogen to the amount of hydrogen remaining in the melt. Table II lists the aluminum parameters used in this study.

Table II Property Parameters of Aluminum Used in the Calculation with Respect to the Present Model
Full size table

Figure 10(a) compares the calculated porosity to the experimental data as a function of the temperature gradient. The discrepancy in porosity increases as the temperature gradient decreases. Therefore, to explain the increase in porosity as the temperature gradient decreases, other factors besides the hydrogen content diffusing from the solid into pores and the change in pore volume should be considered.

Fig. 10
figure 10

Comparison between the calculated values (dotted line) of porosity and the experimental data (solid line) from the influences of (a) temperature gradient and (b) melt temperature on porosity of lotus aluminum. Porosity is evaluated in terms of Yamamura’s model by fitting the calculated value to the experimental result of porosity at (a) temperature gradient of 12.5 K/minute and (b) melt temperature of 1173 K (900 °C)

Full size image

4.4 Effect of Melt Temperature on Porosity and Pore Size

As the melt temperature increases, the concentration of hydrogen dissolved in the liquid phase increases along the liquidus. When the temperature decreases during directional solidification, the concentration of hydrogen decreases along the liquidus up to the equilibrium solubility of hydrogen. Therefore, the porosity of lotus metals should be independent of the melt temperature. Consequently, the effect of melt temperature on pore morphology has not been investigated. On the other hand, in Yamamura’s model the porosity is evaluated by considering the hydrogen concentration dissolved in the liquid phase due to the change in the melt temperature. Considering that the initial concentration of hydrogen dissolved in the liquid phase changes in accordance with the melt temperature, the porosity in lotus aluminum is evaluated with change of the melt temperature of aluminum based on Yamamura’s model. However, Yamamura’s model is not suited to lotus aluminum because the model was originally designed for lotus copper, which has a sufficient hydrogen solubility, and lotus aluminum has a low hydrogen solubility.

To fit the calculated value to the experimental value at the melt temperature 1173 K (900 °C), a was set to 1.0 using the parameters in Table II. Figure 10(b) shows the dependences of the measured and evaluated porosities on the melt temperature. Although both porosities exhibit positive temperature dependences, the calculated porosity is much smaller than the measured one, suggesting more hydrogen than the increment of hydrogen concentration due to the increase in the melt temperature flows into pores to increase the porosity. Consequently, other factors should also be considered.

4.5 Mechanism of Pore Formation in Lotus Aluminum

As mentioned above, the porosity of lotus aluminum in the present work depends on not only hydrogen partial pressure but also the solidification velocity, temperature gradient, and melt temperature. These dependencies are similar to those of dual-phase formation in eutectic alloys; the flux of solute atoms due to solidification conditions affects the morphology of the phases. This suggests that a change in the hydrogen flux by different solidification conditions significantly affects pore formation in lotus aluminum.

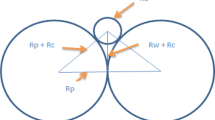
Table III compiles the solubility difference of hydrogen at the melting point between the liquid and solid as well as the diffusion coefficients of hydrogen at the melting point in aluminum and copper. The solubility difference of hydrogen in aluminum is more than one order of magnitude smaller than that in copper, whereas the diffusion coefficients are similar in both aluminum and copper. To promote pore growth in lotus aluminum, hydrogen in aluminum should diffuse over a longer distance than in copper because the solubility of hydrogen is lower in aluminum. Figure 11 schematically depicts the effect of a long diffusion distance of hydrogen rejected in a solid in the vicinity of the solid/liquid interface on pore evolution in lotus aluminum. Assuming the diffusion distance of hydrogen increases, the porosity and pore diameter in lotus aluminum increase as the number of hydrogen atoms increase, resulting in the formation and growth of pores. Thus, the mechanism for pore evolution in lotus aluminum may be the opposite of the mechanism for lotus copper and stainless steel where the formation and growth of pores easily occur even for short distant diffusion of hydrogen due to the high content of hydrogen rejected in the solid. Therefore, the condition of a lower solidification velocity is certainly crucial to realize highly porous lotus aluminum.

Table III Hydrogen Solubility Difference in Liquid and Solid Metals (Aluminum and Copper), and Diffusion Coefficients in Liquid
Full size table
Fig. 11
figure 11

Two-dimensional model for the growth of unidirectional pores near the liquid/solid interface. Hydrogen rejected in solidified aluminum accumulates in the liquid near the liquid/solid interface. (a) When the solidification velocity is fast, hydrogen diffuses only a short distance. Consequently, the impact of hydrogen on growth is small, leading to small pores and a low porosity. (b) When the solidification velocity is slow, hydrogen diffuses over a longer distance. Because a large amount of hydrogen contributes to growth, large pores and a high porosity are obtained

Full size image

The porosity and pore diameter decrease as the solidification velocity and temperature gradient increase, but increase as the hydrogen partial pressure and melt temperature increase. Previous works have reported the effects of solidification velocity and hydrogen partial pressure on pore formation of lotus metals. However, the influence of solidification velocity on pore formation in lotus aluminum differs from previous reports using other lotus metals such as copper[21] and stainless steel.[22] Similar to the fabrication of lotus copper or stainless steel, the pore diameter decreases as the solidification velocity increases. However, unlike for lotus aluminum, the porosity for lotus copper or stainless steel is independent of solidification velocity. Such a difference is attributed to the hydrogen solubility between the liquid and solid phases. For example, the hydrogen solubility gap between the liquid and solid phases in aluminum (4.93 × 10−4 mol pct under H2 0.1 MPa[16]) is about 40 times smaller than that of copper (2.09 × 10−2 mol pct at H2 0.1 MPa[17]) (Table III), but there is not a significant difference in the diffusion coefficients.[27,28] Therefore, the supersaturated hydrogen atoms in aluminum have to migrate a relatively long distance toward the pores to contribute to pore formation and growth. For a fast solidification velocity, the hydrogen atoms in aluminum cannot migrate a sufficient distance to grow large pores. On the other hand, for a slow solidification velocity, the hydrogen atoms in aluminum can migrate a longer distance, allowing more supersaturated hydrogen atoms to contribute to pore formation and growth, producing a larger porosity.

Next, we discuss effects of a hydrogen flux, which depends on the solidification conditions, on pore formation in lotus aluminum. In eutectic alloys, the morphology of a lamellar or rod structure is affected by solidification conditions. Such a change is due to the change in the flux of the solute. For a binary system composed of metal and hydrogen, we consider a dual phase, which consists of a combination of pores and aluminum. Figure 12 shows a two-dimensional model for the competitive growth between directional pores and solid aluminum under steady state conditions. In the present work, the dual phase can be treated in two dimensions, and due to symmetry, only half of a lamellae for each phase needs to be considered.[29] As shown in Figure 12, aluminum rejects hydrogen atoms due to the solubility gap in the melt, whereas the pore rejects aluminum atoms during unidirectional solidification. As well as the solute distribution in the eutectic structure, the mass of diffusing hydrogen (aluminum) atoms into pore (aluminum) per unit of time can be obtained by solving the diffusion equation for solute in the diffusion layer at the solidification front. Therefore, when the z-axis is parallel to the solidification direction and the y-axis is perpendicular to the solidification direction in the y-z coordinate system (Figure 12), the distribution of the solute concentration, C, at the solidification front can be expressed by[29]

Fig. 12
figure 12

Schematic drawing of the diffusion flux of hydrogen and aluminum during pore evolution and growth in the solidification front

Full size image
$$ C = C_{0} + A\exp \left( {\frac{ - Vz}{D}} \right) + B\exp \left( {\frac{ - 2\pi z}{\lambda }} \right)\cos \left( {\frac{ - 2\pi y}{\lambda }} \right), $$
(2)

where C 0 and D are concentration (mol) and diffusion coefficient (m2/s) of solute in molten metal, respectively. V is the growth velocity (m/s) and λ is the distance between periodic phase structure (m). Here A and B are respectively

$$ A = f\left( {C_{\text{S}}^{\beta } - C_{\text{S}}^{\alpha } } \right) + C_{\text{E}} - C_{\text{S}}^{\beta } , $$
(3)
$$ B = \frac{{f(1 - f)V\lambda \left( {C_{\text{S}}^{\beta } - C_{\text{S}}^{\alpha } } \right)}}{2D\sin (\pi f)} $$
(4)

where f is the volume fraction of the α phase, \( C_{\text{S}}^{\alpha } \) and \( C_{\text{S}}^{\beta } \) are the solid solubility limit of B atoms in the α and β phases (mol/m3), respectively. When B atoms are rejected by the α phase and diffuse into the β phase through y = fλ/2, the flux of B atoms, J (mol/s/m2) is obtained by

$$ J = - D\left( {\frac{\partial C}{\partial y}} \right)_{{y = \frac{f\lambda }{2}}} = \pi f\left( {1 - f} \right)V\left( {C_{\text{S}}^{\beta } - C_{\text{S}}^{\alpha } } \right)\exp \left( { - \frac{2\pi z}{\lambda }} \right) $$
(5)

Here, the width of the inspissated solute layer (diffusion layer) is considered to be about λ/2. When a small distance dl is solidified, the amount of diffusing hydrogen, C dl (mol/m), into the nearby phase through the small ∆l is given by

$$ J_{dl} = \int\limits_{0}^{\lambda /2} {Jdz \times \frac{dl}{V} = f(1 - f)} \left( {C_{\text{S}}^{\beta } - C_{\text{S}}^{\alpha } } \right)\lambda dl $$
(6)

where α and β are the aluminum and pore phases, respectively, and A and B atoms denote aluminum and hydrogen atoms, respectively. \( {\text{C}}_{\alpha } \) and \( {\text{C}}_{\beta } \) are the hydrogen solubility in solid aluminum and the gas phase (mol/m3), respectively. Because solid aluminum is not dissolved in the gas phase, the molar ratio of hydrogen is equal to 1. Therefore, \( {\text{C}}_{\alpha } \) and \( {\text{C}}_{\beta } \) are expressed as

$$ C_{\alpha } = \frac{{\eta_{{T_{n} }} }}{{V_{\text{Al}} }} \times \sqrt {P_{{{\text{H}}_{2} }} } , $$
(7)
$$ C_{\beta } = \frac{{2RT_{n} }}{P} \times \sqrt {P_{{{\text{H}}_{2} }} } . $$
(8)

Here the volume fraction in the equilibrium phase diagram is used as the volume fraction f. However, because the porosity of lotus aluminum depends on the solidification conditions, the volume fraction of aluminum phase f is obtained from the experimental results. In the present work, Yamamura’s model for mass balance of lotus copper is modified by considering hydrogen diffusion, i.e., the terms indicating the mass of hydrogen are substituted using Eqs. [4] through [6].

[Initial amount of hydrogen contained in the liquid in the volume element]

+ [Amount of hydrogen contained in the liquid flowing into the volume element to compensate for solidification shrinkage]

− [Amount of hydrogen contained in the liquid flowing out of the volume element due to pore formation]

+ [Amount of hydrogen dissolved in solid copper around the pore with a length of l + dl].

In Yamamura’s model, the hydrogen mass balance for a unit length as the solidification front advances dl is considered. Because the number of pores per unit length and supplied hydrogen from both sides of the pores have to be considered as the solidification front advances dl, the mass of diffusing hydrogen is written as

$$ W_{\text{H}} = f(1 - f)(C_{\beta } - C_{\alpha } )\lambda \times \frac{2}{\lambda } \times \frac{M}{2}dl $$
(9)

In the present work, λ is given by following equation using porosity ε [pct] where pore diameter d p [m] given by experimental results

$$ \lambda = \frac{{d_{\text{p}} }}{\varepsilon } $$
(10)

Equation [9] is substituted in Yamamura’s model and the porosity of lotus metal is expressed as

$$ \varepsilon = \frac{{fM(1 - f)(C_{\beta } - C_{\alpha } ) + \left( {\eta_{{T_{n} }} - \eta_{{T_{n} - Gl}} } \right)\sqrt P \times \frac{M}{{2V_{\text{Al}} }}}}{{\frac{MP}{{R(T_{n} - Gl)}} + \left( {\eta_{{T_{n} }} - \eta_{{T_{n} - Gl}} } \right)\sqrt P \times \frac{M}{{2V_{\text{Al}} }}}} $$
(11)

Table II lists the values of select aluminum characteristics used in the calculation. Figure 13 shows the dependence of porosity on (a) solidification velocity, (b) hydrogen partial pressure, (c) melt temperature, and (d) temperature gradient. To compare the experimental results and the calculated results predicted using Eq. [11] with Yamamura’s model,[21] closed circles, open circles, and the dotted line denote the experimental results, calculated results using Eq. [11], and the results predicted by Yamamura’s model, respectively. The calculated porosities using Eq. [11] agree well with the experimental results. In Yamamura’s model, we calculated the porosity by assuming that all of the rejected hydrogen atoms due to the solubility gap form pores; parameter a = 1. Although the dependence of the porosity calculated from Yamamura’s model on the hydrogen partial pressure is consistent with the experimental results, the dependence of the porosity for the other factors using Yamamura’s model is inconsistent with the experimental results. These observations are reasonable because Yamamura’s model does not consider the effect of the solidification condition.

Fig. 13
figure 13

Dependence of porosity on (a) solidification velocity, (b) hydrogen partial pressure, (c) melt temperature, and (d) temperature gradient. Closed and open circles indicate experimental data and the calculated results using Eq. [11], respectively. Dotted lines are the predicted results using Yamamura’s model

Full size image

Moreover, even if all of hydrogen atoms rejected in the solidified metal evolves into pores, the maximum porosity calculated by Yamamura’s model is less than 15 pct, which is far below the maximum experimental porosity of 40 pct. This discrepancy suggests that the contribution of hydrogen diffusion in the melt rejected in the solid phase near the solid/liquid interface is critical. Thus, control of solidification conditions such as the solidification velocity, hydrogen partial pressure, temperature gradient, and melt temperature is crucial to increase the porosity of lotus metal with a low hydrogen solubility.

Finally, the present model is applied to previous experimental results on the dependence of porosity on the solidification velocity for lotus copper, which shows a different tendency from lotus aluminum. Figure 14 compares the experimental results and the results calculated using Eq. [11] for the solidification velocity dependences of porosities of lotus aluminum and copper.[25] Because the dependence of porosity on the temperature gradient during unidirectional solidification for lotus copper was not reported, we calculated the porosity assuming temperature gradients of 10, 30, and 50 K/mm. The calculated porosities for lotus copper based on the present model are consistent with the tendencies observed in the experimental results. Thus, it is concluded that the pores in lotus metal are formed predominantly due to hydrogen diffusion in the melt rejected by solidified metal. This pore formation mechanism is similar to that of eutectic phase structure formation.

Fig. 14
figure 14

Dependence of porosity of aluminum and copper[25] on the solidification velocity. Experimental results and the results calculated using Eq. [11] are shown

Full size image

5 Conclusions

Lotus-type porous aluminum is fabricated by the continuous casting technique in pressurized hydrogen or a mixed gas of hydrogen and argon. The porosity and pore size increase with increasing hydrogen partial pressure or melt temperature, while those decrease with increasing solidification velocity or temperature gradient. Since the hydrogen solubility is low in aluminum, low solidification velocity is crucial to obtain high porosity of lotus aluminum. It is concluded that the diffusion of hydrogen rejected in the solidified aluminum near the solid/liquid interface is the most important for pore formation.