Micro–macro multilevel latent class models with multiple discrete individual-level variables

Abstract

An existing micro–macro method for a single individual-level variable is extended to the multivariate situation by presenting two multilevel latent class models in which multiple discrete individual-level variables are used to explain a group-level outcome. As in the univariate case, the individual-level data are summarized at the group-level by constructing a discrete latent variable at the group level and this group-level latent variable is used as a predictor for the group-level outcome. In the first extension, that is referred to as the Direct model, the multiple individual-level variables are directly used as indicators for the group-level latent variable. In the second extension, referred to as the Indirect model, the multiple individual-level variables are used to construct an individual-level latent variable that is used as an indicator for the group-level latent variable. This implies that the individual-level variables are used indirectly at the group-level. The within- and between components of the (co)varn the individual-level variables are independent in the Direct model, but dependent in the Indirect model. Both models are discussed and illustrated with an empirical data example.

1 Introduction

In many research areas, data are collected on individuals (micro-level units) that are nested within groups (macro-level units) (Goldstein 2011). For example, data can be collected on children nested in schools, on employees nested in organizations, or on family members nested in families. The variables involved may be either measured at the individual level or at the level of the groups. Following, Snijders and Bosker (2012), one can distinguish between macro–micro and micro–macro situations. In a macro–micro situation, the outcome or dependent variable is measured at the individual level, while in a micro–macro situation, the outcome variable is measured at the group level. The current article focuses on the latter type of multilevel analysis that is needed when, for example, characteristics of household members are related to household ownership of financial products, or when psychological characteristics of employees are related to organizational performance outcomes. Furthermore, attention is focused on micro–macro analysis for discrete data.

In micro–macro analysis, the individual-level data need to be aggregated to the group level, so the aggregated scores can be related to the group-level outcome. When a group mean or mode is used for aggregation, measurement and sampling error in the individual scores is not accounted for and Croon and van Veldhoven (2007) showed that this neglect of random fluctuation in the individual scores causes bias in the estimates of the group-level parameters. Moreover, this type of aggregation wipes out all individual differences within the groups and it is well known that the variability of the group means and modes not only represents between-group variation but also partly reflects within-group variation. Therefore, the analysis of observations from micro–macro designs requires an appropriate methodology that takes into account the measurement and sampling error of the individual scores and neatly separates the between- and within-group association among the variables (Preacher et al. 2010).

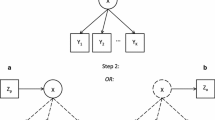
Such techniques have been developed by using a group-level latent variable for the aggregation. For continuous data, Croon and van Veldhoven (2007) provide a basic example of this methodology. The scores of the individuals i from group j on an explanatory variable $Z_{ij}$ are interpreted as exchangeable indicators of an unobserved group score on the continuous latent group-level variable $\zeta _j$. Furthermore, the latent variable is treated as a group-level mediating variable between a group-level predictor $X_j$ and a group-level outcome $Y_j$. Figure 1 represents this model graphically. Any theory in which a group-level intervention is not only expected to influence a group-level (performance) measure directly, but also indirectly through a characteristic of the group members, can be tested with this model.

Fig. 1

Micro–macro latent variable model with one micro-level variable

The model belongs to the general framework of generalized latent variable models described by Skrondal and Rabe-Hesketh (2004) and can also be formulated for categorical data (Bennink et al. 2013), by using a latent class model instead of a factor–analytic model that was used for continuous variables. The latent variable $\zeta _j$ then becomes a categorical variable with C categories, $c=1,\ldots ,C$. The scores $Z_{ij}$ of the $I_j$ individuals in group j (collected in the vector $\mathbf{Z}_j$) are treated as ‘unreliable’ indicators of the group score $\zeta _j$. For an arbitrary group j, the relevant conditional probability distribution for the manifest variables $Y_j$ and $\mathbf{Z}_j$ given $X_j$ is:

$$\begin{aligned} P(Y_j, \mathbf{Z}_j|X_j) = \sum _{c=1}^C{P(Y_j, \zeta _j=c|X_j)P(\mathbf{Z}_j|\zeta _j=c)}. \end{aligned}$$

(1)

The terms on the right hand side of the equation are the between and within part that can be further decomposed as

$$\begin{aligned} P(Y_j, \zeta _j=c|X_j) = P(\zeta _j=c|X_j)P(Y_j|X_j, \zeta _j=c), \end{aligned}$$

(2)

and

$$\begin{aligned} P(\mathbf{Z}_j|\zeta _j=c) = \prod _{i=1}^{I_j}{P(Z_{ij}|\zeta _j=c)}. \end{aligned}$$

(3)

Since in the social and behavioral sciences it is very common to use multiple individual-level variables instead of only a single one, in the present article two multilevel latent class models are presented that extend the univariate case to the situation with multiple $Z_{ij}$-variables. As in the existing method, the $Z_{ij}$-variables are summarized by a single discrete latent variable at the group level ($\zeta _j$). In the first model, that is referred to as the Direct model, the $Z_{ij}$-variables are directly used as indicators for $\zeta _j$, while in the second model, that is referred to as the Indirect model, this is done indirectly through an individual-level latent variable ($\eta _{ij}$). The Direct model can, for example, be used to construct a latent classification of households based on the age, gender and educational level of the household members to predict household ownership of financial products. In other words, individual-level information can be summarized at the group-level by constructing a group-level typology based on the individual-level variables. The Indirect model can, for example, be used when multiple individual-level items on the satisfaction of employees with respect to their relationships at work are used to construct the individual-level latent variable $\eta _{ij}$ that is used as an indicator for $\zeta _j$ to predict organizational performance measures, such as the level of organizational conflicts. The Indirect model makes it possible to allow groups to differ with respect to the proportion of individuals that belong to the various individual-level latent classes. In the remaining article, both methods and their estimation procedures are discussed and applied to empirical data examples.

2 Direct model

Figure 1 is extended to a situation with K individual-level variables. These individual-level variables $Z_{1ij}, Z_{kij}\ldots Z_{Kij}$, can be directly used as indicators of the discrete latent group-level variable $\zeta _j$, as done in the model with a single $Z_{kij}$. In this way, a (latent) typology of groups is constructed based on the multiple individual-level variables. For example, the age, gender and educational level of household members can be used to construct a classification of households. This classification of groups is used as a predictor for the observed group-level outcome $Y_j$, for example, the household ownership of a financial product. An application with three group-level outcomes is shown in the Empirical data example section. Also other (observed) group-level predictors represented by $X_j$, can be included in the model. For example, the household income can be used as an additional group-level predictor.

Although not necessarily in a model with a single $Z_{kij}$, in a model with multiple $Z_{kij}$-variables it needs to be accounted for that the individual-level variables can be dependent within individuals, since it is not reasonable to assume that all of the association between the individual-level indicators is explained by $\zeta _j$. This can be done in two ways. As a first alternative, all two-way within associations among the $Z_{kij}$-variables can be incorporated in the model as shown in the left panel of Fig. 2. This model is referred to as the ‘Direct_ass model’. A second alternative consists of defining a discrete individual-level latent variable $\eta _{ij}$ with D categories, $d=1,\ldots ,D$, as shown in the right panel of Fig. 2. This model is referred to as the ‘Direct_lv model’.¹

Fig. 2

Direct models

As in Eq. (1), the probability distribution of an arbitrary group j contains a between and a within term. For both models the between part is still represented by Eq. (2), but they differ with respect to the within part. For the Direct_ass model, the within part is

$$\begin{aligned} P(\mathbf{Z}_j|\zeta _j=c) = \prod _{i=1}^{I_j}{P(Z_{1ij},\ldots Z_{kij},\ldots Z_{Kij}|\zeta _j=c)}, \end{aligned}$$

(4)

whereas for the Direct_lv model, the within part is

$$\begin{aligned} P(\mathbf{Z}_j|\zeta _j=c) = \prod _{i=1}^{I_j}{\sum _{d=1}^D{P(\eta _{ij}=d)\prod _{k=1}^K{P(Z_{kij}|\zeta _j=c, \eta _{ij}=d)}}} . \end{aligned}$$

(5)

The group members are used as exchangeable indicators, this implies that $P(Z_{1ij}, Z_{kij},\ldots Z_{Kij}|\zeta _j=c)$ in the Direct_ass model and $P(Z_{kij}|\zeta _j=c, \eta _{ij}=d)$ in the Direct_lv model, are identical for all individuals. In the Direct_ass model, there is by definition local dependency among the indicators given $\zeta _j$, but in the Direct_lv model, the indicators are locally independent given $\eta _{ij}$ and $\zeta _j$. It is also important to note is that $\eta _{ij}$ and $\zeta _j$ are assumed to be independent.

3 Indirect model

When the K individual-level variables were intended in the first place to measure an individual-level construct, the relationship between the group-level latent variable and the individual-level items can be specified indirectly rather than directly. For example, suppose that the satisfaction of employees with their relationships at work is measured by three indicators: (1) their satisfaction with the relation with their supervisor, (2) the satisfaction with their relation with other coworkers, and (3) the degree in which they experience a family culture at their working environment. These three $Z_{kij}$-variables may be treated as indicators of an underlying latent construct at the individual-level ($\eta _{ij}$). In the current article $\eta _{ij}$ is a discrete variable with D categories, $d=1,\ldots ,D$.² Since there may exist group differences on $\eta _{ij}$, a group-level latent variable ($\zeta _j$) may be invoked to represent these between-group differences on $\eta _{ij}$.

This model containing a single group-level outcome $Y_{j}$ is graphically shown in Fig. 3 and referred to as the ‘Indirect model’. We will show an example with two group-level outcomes in the Empirical data examples section.

Fig. 3

Indirect model

Referring to the formal general description in Eq. (1), the between part of this model is represented again by Eq. (2), but the within part is now:

$$\begin{aligned} P(\mathbf{Z}_j|\zeta _j=c) = \prod _{i=1}^{I_j}{\sum _{d=1}^D{P(\eta _{ij}=d|\zeta _j=c) \prod _{k=1}^K{P(Z_{kij}|\eta _{ij}=d)}}}. \end{aligned}$$

(6)

The group members are again treated as exchangeable, so that $P(Z_{kij}|\eta _{ij}=d)$ has the same form for all individuals. The individual-level variables are locally independent given $\eta _{ij}$ and the two latent variables are dependent since the distribution of $\eta _{ij}$ depends on $\zeta _j$. In this model there is no immediate need to allow for residual association among the individual indicators since $\eta _{ij}$ is assumed to account for all of the associations that exist among the indicators.

4 Estimation, identification, and model selection

The micro–macro models presented above are extended versions of the multilevel latent class model proposed by Vermunt (2003). The extension involves that, in addition to having discrete latent variables at two levels, these models contain an outcome variable at the group level. Vermunt (2003) showed how to obtain maximum likelihood estimates for multilevel latent class models using an EM algorithm, and a very similar procedure can be used here. The log-likelihood to be maximized equals:

(7)

while the complete data likelihood equals:

$$\begin{aligned} L_{comp}= & {} \prod _{j=1}^{J}{P(Y_{j},\mathbf {Z}_{j}, X_{j}, \zeta _{j}, \mathbf {\eta }_{j})} \nonumber \\= & {} \prod _{j=1}^{J}{\left[ P(X_j)P(\zeta _{j}|X_{j})P(Y_{j}|X_j, \zeta _{j}) \prod _{i=1}^{I_{j}}{P(\eta _{ij}|\zeta _{j})P(Z_{ij}|\zeta _{j},\eta _{ij})} \right] } {.} \end{aligned}$$

(8)

The expected complete-data log-likelihood, which is computed in the E-step and maximized in the M-step, has the following form:

$$\begin{aligned} E(\log ~L_{comp})= & {} \sum _{j=1}^{J}\sum _{c=1}^{C}\pi _{j}^{c}\log {~P(\zeta _{j}=c|X_{j})} \nonumber \\&{+\sum _{j=1}^{J}\sum _{c=1}^{C}\pi _{j}^{c}\log P(Y_{j}|X_j,\zeta _{j}} {=c)} \nonumber \\&{+\sum _{j=1}^{J}\sum _{i=1}^{I_{j}}\sum _{c=1}^{C}\sum _{d=1}^{D}\pi _{ij}^{cd}\log P(}\eta _{ij}=d{|\zeta _{j}=c)} \nonumber \\&{+\sum _{j=1}^{J}\sum _{i=1}^{I_{j}}\sum _{c=1}^{C}\sum _{d=1}^{D}\pi _{ij}^{cd}}\log {{P(Z_{ij}|\zeta _{j}=c,\eta {_{ij}=d})}.} \end{aligned}$$

(9)

Here, $\pi _{j}^{c}$ and ${\pi _{ij}^{cd}}$ denote the posterior class membership probabilities $P(\zeta _{j}=c|{Y_{j}},\mathbf {Z}_{j},X_{j})$ and $P(\zeta _{j}=c,\eta _{ij}=d|{Y_{j},}\mathbf {Z}_{j},X_{j})$, respectively. These posterior probabilities can be obtained in an efficient manner using an upward–downward algorithm. In the upward step we obtain $\pi _{j}^{k}$ and in the downward step we obtain ${\pi _{ij}^{cd}}$ as $\pi _{j}^{c}P( \mathbf {\eta }_{ij}=d|\zeta _{j}=c,{Y_{j}},\mathbf {Z}_{ij},X_{j})$. This algorithm is implemented in the Latent GOLD program (Vermunt and Magidson 2013) that we used for parameter estimation in the empirical examples presented in the next section.

Since the four sets of model probabilities are parametrized using logit models, the M step involves updating the estimates of a set of logistic parameters in the usual way. Note that the three special cases of the micro–macro model are all restricted versions of the general model for which we defined the expected complete-data log-likelihood. The Direct_ass model does not contain a lower-level latent variable, which can be specified by setting $D=1$. In this model, the joint distribution of $\mathbf {Z}_{ij}$ is modeled with a multivariate logistic model containing the two-variable associations between the responses. In the Direct_lv model and the Indirect model, we assume responses $Z_{kij}$ to be locally independent, meaning that the associations between the responses are fixed to zero. Moreover, in the former $Z_{kij}$ is assumed to be independent of $\zeta _{j}$ given $P(Z_{1ij},\ldots Z_{kij},\ldots Z_{Kij}$ and in the latter $\eta {_{ij}}$ is assumed to be independent of $\zeta _{j}$, which are restrictions that can be obtained by fixing the logistic parameters concerned to zero.

As regards the identifiability of the models proposed in this article, similar conditions apply as for regular latent class models. There is no sufficient and necessary condition available to unassailable determine the identifiability of complex latent class models. A sufficient, but not necessary, condition for identification is that both the individual- and the group-level part of the model are identified latent class models (Vermunt 2005). For the individual-level model this means that we need at least three $Z_{kij}$-variables ($K\ge 3$), whereas for the group-level model this means that most groups should have at least three individuals ($I_{j}\ge 3$). However, also when these conditions are not fulfilled, the micro-macro model concerned may be identified. For example, the Direct_ass model, which contains only a group-level latent variable, is also identified with two individuals per group when $K\ge 2$, and the Indirect model is also identified with $K=2$ and $I_{j}\ge 3$. A formal way to check identification is to determine the rank of the Jacobian matrix and the empirical identifiability, and not the algebraic identifiability, of a model can be checked in Latent GOLD.

Another important issue concerns the selection of the number of classes at the individual and the group level. For multilevel latent class models, Lukočiene et al. (2010) recommended to use either the BIC (with the number of groups as sample size in the formula) or the AIC3 for making this decision. In the Direct_ass model, there is only a group-level latent variable, meaning that we can simply select the model with the number of group-level classes that provides the best fit. For the Direct_lv model and the Indirect model, on the other hand, the number of classes at both levels have to be determined simultaneously. Here, we follow the suggestion by Lukočiene et al. (2010) to first determine the number of classes at the individual-level (D), keeping the number of group-level classes fixed to one ($C=1)$. The second step is then to fix D at this value to determine the number of group-level classes (C). In the final step, the number of individual-level latent classes (D) is reconsidered again while fixing C at the previously determined value.

5 Empirical data examples

In this section, the Direct_ass model and the Indirect model are applied to empirical data. In the first example, data on Italian households are used to investigate how demographic characteristics of the household members affect household ownership of financial products. Contrarily to Fig. 2, this example does not contain an additional group-level predictor $X_j$. In the second example, data on small firms are used to investigate how the perceived quality of employees of their relationships at work affects organizational performance measures, and whether this relationship is moderated by organizational size. Both examples contain multiple group-level outcome variables and residual associations among these outcomes are included in the models because there might me association among the outcome variables that cannot be explained by the explanatory variables in the model. A Wald test can be used to test whether these associations are significant. All analyses are carried out in Latent GOLD 5.0 (Vermunt and Magidson 2013).

5.1 Example Direct model

From the 2010 Survey of Italian Household Budgets (Bank of Italy 2012), information is available on the ownership of financial products by 7951 Italian families. Three such financial products are taken here as group-level outcomes: the number of postal and bank accounts (ACC), the number of postal and bank savings accounts (SAV), and the number of credit cards (CRD). In the same survey, information is available on various demographic characteristics, such as age (AGE), educational level (EDU), and sex (SEX), of the 19836 individual family members. These individual-level variables are used to construct a latent typology of the families ($\zeta _j$). The research question of interest is whether these different types of households show significant differences with respect to ownership of the three financial products. The Direct model can be used to answer this research question since the individual-level demographical information is summarized at the family level to construct a (latent) typology of families. At the same time can be investigated whether these typology of families differs with respect to their consumer behavior.

For the analysis, the variables on ownership of the financial products were categorized into two categories: either the family owned the financial product (score $=$ 1) or it did not (score $=$ 0). For the variables measured at the individual-level, age and educational level were categorized into five categories (1 $=$ $<$30, 2 $=$ 30–40, 3 $=$ 41–50, 4 $=$ 51–65, 5 $=$ $>$65; 1 $=$ none, 2 $=$ elementary school, 3 $=$ middle school, 4 $=$ high school, 5 $=$ bachelor or higher) and sex had two categories (1 $=$ male, 2 $=$ female).

For the Latent GOLD analyses, six multinomial logit equations were defined, one for each group-level outcome and one for each individual-level variable. In all equations, a discrete group-level variable $\zeta _j$ was used as a predictor. All two-way associations among the group-level outcomes and all two-way associations among the individual-level variables were specified as well. The model is graphically displayed in Fig. 4.

Fig. 4

Example Direct model

Both the selection criteria BIC (based on the number of groups) and AIC3 suggested a model with at least 18 household-level classes. This large number of latent classes required to obtain an acceptable statistical fit is probably a consequence of the huge size of the sample on which the analyses were carried out, but it simply precludes a straightforward and illuminative interpretation of the results. For illustrative purposes, the solution with three classes is interpreted here. These classes are well separated as indicated by the Entropy R-squared measure (Vermunt and Magidson 2005), $R^2_{entr}=.74$, that is in general labeled to be good when it is larger than .70. Latent GOLD was used to check whether the model is empirically identified.

Table 1 Class proportions and class-specific probabilities Example Direct model

The estimates of the logit parameters of the fitted model are all significant at the 1 % significance-level and the model contained 65 parameters: two intercepts for the group-level latent classes (two parameters), four intercepts and eight slopes for age and educational level and one intercept and two slopes for sex (2 $\times$ 12 + 1 $\times$ 3 = 27 parameters), an intercept and two slopes for each of the three group-level outcomes (3 $\times$ 3 = 9 parameters), 24 parameters were needed to model all the two-way associations among the individual-level variables, and three parameters were needed to model the two-way associations among the group-level outcomes (24 + 3 $=$ 27 parameters).

The corresponding class-specific response probabilities together with the class proportions are given in Table 1. The first group-level class contains 36 % of the households. From Table 1a can be seen that the household members in this class are relatively old, lowly educated and a small majority of the family members is female. The second group-level class contains 32 % of the households. The members from this class are relatively young, moderately educated with an equal balance between males and females. Finally, the third group-level category contains also 32 % of the households. The members are relatively old, highly educated and gender is again equally distributed.

From Table 1b can be seen that, compared to the other two classes, the households from the first class have the lowest probability to own bank accounts (.72), the highest probability to own savings accounts (.25), and a very low probability to own credit cards (.08). The households from the second class have a higher probability to own bank accounts (.85) than the households from the first class (.72) but a lower probability than the households from the third class (.97). They have a lower probability to own savings accounts (.19) than the first class (.25) but a higher probability than the third class (.16). With regard to credit cards, the second type of households is in the middle of the other two classes as well (.38). The households from the third class have the highest probability to own bank accounts (.97) and credit cards (.53) but the lowest probability to own savings accounts (.16).

The two-way associations among the individual-level variables are all significant at the 1 % significance level. Since they were only included in the model to account for any residual within-group association that could not be explained at the group-level and not for substantive reasons, the estimates of the associations are not reported here. The two-way associations among the group-level outcomes are all significant at the 5 % significance level. The number of postal and bank accounts and the number of postal and bank savings accounts are negatively related ($r=-1.01, Wald=185.14, df=1, p<.001$), while the number of postal and bank accounts and the number of credit cards, as well as the number of postal and bank savings accounts and the number of credit cards, are positively related ($r=4.81, Wald=92.30, df=1, p<.001$; $r=0.23, Wald=10.37, df=1, p=0.0013$).

To conclude, our analysis yielded a classification of the households in three types that especially differ in composition with respect to age and educational level of the family members. Moreover, the different types of households show clear differences with respect to ownership of financial products. The households with older, lower educated members have a higher probability of owning savings accounts than the other two types of households, but a lower probability of owning bank accounts or credit cards. The households with relatively young and moderately educated members have the highest probability to own savings accounts and fall in between the other two classes with respect to owning bank accounts and credit cards. The households with relatively old and highly educated members have the highest probability to own bank accounts and credit cards, and fall in between the other two classes with respect to savings accounts.

5.2 Example Indirect model

In the literature on small-firm Human Resource Management (HRM), it is often assumed that working in a small firm is either fantastic or gruesome (Wilkinson 1999). This assumption is tested on data collected by Dr. B. Kroon by administering two questionnaires. In the first questionnaire, 96 HR managers of small organizations provided information about their HR system and other organizational characteristics. In the second questionnaire, 516 employees provided information about their perceptions of work-related issues, such as their experience of positive relationships at work. The research question of interest is how the perception of employees on their relationships at work affects two organizational performance measures: the level of absenteeism and the amount of conflict in the organization. At the same time, it is investigated whether this relationship is moderated by organizational size. The Indirect model is used to explore this theory since the individual-level variables are intended to measure an individual-level (latent) construct. The individual-level latent classes are aggregated to the group-level using group-level latent classes so the individual-level information can be used at the group level to explain the group-level outcome variables.

Organizational size (SIZE) was measured by the total number of employees in the organization, including working owners and part-time employees, as reported by the HR manager. The variable is dichotomized into two categories; one with firms having less than ten employees, and one with firms having 11–50 employees. This corresponds to micro organizations and small organizations as defined by the European Commission (2005). The level of absence (ABS) and industrial conflict (CON) was originally measured on a five point Likert scale ranging from very low to very high (Guest and Peccei 2001). Since the scores reported by the HR managers were very skewed, the variables are dichotomized to organizations that have very low levels (Cat $=$ 1) and low to very high levels (Cat $=$ 2) of absenteeism or conflict.

At the individual-level, the perception of work relationships were measured by three indicators: (1) satisfaction with the direct supervisor (SUP), (2) satisfaction with colleagues (COL), and (3) the perception of the degree in which the individual experience a family culture at work (FAM). These three indicators were originally measured with multiple items, but to keep the illustration simple and as close as possible to Fig. 3, the mean scale scores of each of the three scales are computed and used to construct three categorical variables with three about equally sized categories (low, medium, high). These discrete variables were used as indicator variables in the latent class analysis. Satisfaction with the direct supervisor was originally measured by nine items on a four point Likert scale ranging from never to always (Van Veldhoven et al. 2002). An example item is: ”Can you count on your supervisor when you come across difficulties in your work?”. Satisfaction with colleagues was originally measured with the same four answer categories on six items (Van Veldhoven et al. 2002). An example item is: ”If necessary, can you ask your colleagues for help?”. The perception of a family culture at work was originally measured by three items on a five point scale ranging from totally disagree to totally agree (Goss 1991). An example item is: ”People here are like family to me”.

The model can be formally described with seven multinomial logit models: (1) two for the group-level outcomes in which the main effect of $\zeta _j$, the main effect of organizational size and their interaction effect are used as predictors, (2) one for the group-level latent variable $\zeta _j$ in which organizational size is used as a predictor, (3) one for the individual-level latent variable $\eta _{ij}$ for which $\zeta _j$ is a predictor, and (4) three for the individual-level variables for which $\eta _{ij}$ is a predictor. Furthermore, a two-variable association among the two firm-level outcomes is added to the model. The model is graphically displayed in Fig. 5 (the effects that were not significant are colored gray).

The number of classes for the two latent variables are determined following the stepwise procedure of Lukočiene et al. (2010) using BIC based on the number of groups. This resulted in two classes at the individual-level and five classes at the group-level. The class separation of the latent variables is sufficient to good ($R_{entr}^{\eta }=.67$ and $R_{entr}^{\zeta }=.92$). Again, Latent GOLD was used to check whether the model is empirically identified.

All effects were significant at the 5 % level, except the main effect of organizational size and its interaction effect with $\zeta _j$ on both group-level outcomes. Therefore, these effects were removed from the model and the final model contains 36 parameters: for each of the three observed individual-level variables, an intercept and three slopes are estimates (3 $\times$ 4 $=$ 12 parameters), for the individual-level latent classes, an intercept and four slopes are estimated (five parameters), for each of the two group-level outcomes an intercept and four slopes are estimated (2 $\times$ 5 $=$ 10 parameters), for the group-level latent classes, four intercepts and four slopes are estimated (eight parameters), and the association among the group-level variables is estimated with an additional parameter (one parameter).

Fig. 5

Example Indirect model

The class proportions and class-specific probabilities based on the final fitted model are given in Table 2. Table 2a shows that at the individual-level, there is one class that contains 53 % of the employees and these employees are not very satisfied with their relationships at work. The second class of individuals contains 47 % of the employees that are satisfied with their relationships at work.

Table 2 Class proportions and class-specific probabilities Example Indirect model

Table 2b provides the conditional probabilities of the discrete categories of the indicators given the discrete categories of the group-level latent variable $\zeta _j$, and the conditional probabilities of the latent categories of $\zeta _j$ given the categories of the group-level predictor organizational size are provided in Table 2c. From the first two rows of Table 2b can be seen that at the group-level, the five classes differ with respect to the composition of employees from the two individual-level classes. The group-level latent classes are ordered from the lowest probability of an employee belonging to the satisfied individual-level class (.19) through the highest (.82). The first and second group-level classes contain firms with employees from the unsatisfied individual-level classes (.81 and .65, respectively). The class sizes are 17 and 13 %. The fourth and fifth group-level classes contain firms that have the highest probability of employees from the satisfied individual-level class (.61 and .82, respectively). These classes contain 39 and 10 % of the firms. The remaining 20 % of the firms belong to the third group-level class. In this class a mixture of employees from the two individual-level classes is found.

In Table 2c is shown that, the micro firms with maximum ten employees (SIZE $=$ 1), have the highest probability to belong to the fourth group-level class (.56) and the small firms with 11–50 employees (SIZE $=$ 2) have the highest probability to belong to the first group-level class (.28). The micro organizations have a higher probability to belong to the fourth class than the small organizations, but for the remaining four classes it is the other way around.

Table 2b shows that the fourth group-level class contains firms with very low probabilities of absenteeism (.00) and conflict (.00). The second and third group-level classes have, respectively, high probabilities on either absenteeism (1.00) or conflict (1.00). The first and fifth group-level classes have high probabilities to encounter both (1.00 and 1.00). The fact that these probabilities are this extreme (.00 and 1.00) is likely to be caused by the fact that before recoding the variables, about half of the firms don’t report any levels of conflict and absenteeism. The association among the levels of absenteeism and conflict is not significant (r=5.26, Wald=.91, df=1, p=.34).

To conclude, at the individual-level, the assumption that working at a firm with less than 50 employees is either fantastic or gruesome is supported, since the two individual-level classes could be interpreted as a satisfied and an unsatisfied class of employees. At the group-level the situation becomes more complex. Although about half of the organizations contain mostly employees from the satisfied individual-level class, these organization belong either to a group-level class that encounters low or high levels of absenteeism and conflict. So at the group-level, there is no clear positive effect of having satisfied employees on organizational levels of absenteeism and conflict. Organizational size matters in this context, since micro organizations have a higher probability to belong to the group-level class with no troubles than small firms.

6 Discussion

In the current article, two latent class models, referred to as the Direct model and the Indirect model, are presented that can be used to predict a group-level outcome by means of multiple individual-level variables by extending an existing method for micro-macro analysis with a single individual-level variable to the multivariate case. Both models involve the construction of a group-level latent class variable based on the individual-level variables to summarize the individual-level information at the group-level. The group-level latent variable can then be related to other group-level variables, such as a group-level outcome. In the Direct model, the group-level latent classes affect the individual-level variables directly, while in the Indirect model these are affected indirectly via an individual-level latent variable. The Direct model seems most appropriate when the aim of the research is to construct a typology of groups that affect one or more group-level outcomes. In this situation the within and between component of the individual-level variables are independent. The Indirect model seems more appropriate when the individual-level variables are intended to measure an individual-level construct and groups are allowed to differ on the individual-level variable. The within and between component of the individual-level variables are now dependent. Both methods are applied to real data examples.

In the models with a discrete latent variable at each level, the number of classes of the latent variables had to be decided simultaneously since the full model was estimated at once. Although Lukočiene et al. (2010) provided guidelines on how to make this decision, further research should be devoted to study whether their approach is also optimal in the current context. Especially when the latent variables are dependent, one might prefer to determine the number of latent classes of the two variables independently. A stepwise procedure to do this without introducing bias in the group-level parameter estimates, is presented in Bolck et al. (2004), Vermunt (2010), and Bakk et al. (2013). A further limitation of the current method is that the group-level outcome functions as an additional indicator of the latent group-level variable. This implies that the formation of the group-level classes is affected by the outcome variable. This may be counter intuitive since the latent variable is intended to predict the outcome. An additional advantage of using the stepwise procedure just referred to, is that the latent classes can not only be defined independent of each other, but also independent of the group-level outcome.