Extragradient algorithms for equilibrium problems and symmetric generalized hybrid mappings

Abstract

In this paper, we propose new algorithms for finding a common point of the solution set of a pseudomonotone equilibrium problem and the set of fixed points of a symmetric generalized hybrid mapping in a real Hilbert space. The convergence of the iterates generated by each method is obtained under assumptions that the fixed point mapping is quasi-nonexpansive and demiclosed at 0, and the bifunction associated with the equilibrium problem is weakly continuous. The bifunction is assumed to be satisfying a Lipschitz-type condition when the basic iteration comes from the extragradient method. It becomes unnecessary when an Armijo back tracking linesearch is incorporated in the extragradient method.

1 Introduction

Let $\mathbb {H}$ be a real Hilbert space with the inner product $\langle \cdot , \cdot \rangle$ and induced norm $\Vert \cdot \Vert$. By ‘$\rightarrow$’ and ‘$\rightharpoonup$’ we denote the strong convergence and the weak convergence in $\mathbb {H}$, respectively. Let C be a nonempty closed convex subset of $\mathbb {H}$ and $f :C \times C \rightarrow \mathbb {R}$ be a bifunction satisfying $f(x, x) = 0$ for every $x \in C$. Such a bifunction is called an equilibrium bifunction. The equilibrium problem, in the sense of Blum, Muu and Oettli [4, 19] [shortly EP(C, f)], is to find $x^* \in C$ such that

$$\begin{aligned} f(x^*, y) \ge 0, \quad \forall y \in C. \end{aligned}$$

(1)

By Sol(C, f), we denote the solution set of EP(C, f). Although problem EP(C, f) has a simple formulation, it includes, as special cases, many important problems in applied mathematics: variational inequality problem, optimization problem, fixed point problem, saddle point problem, Nash equilibrium problem in noncooperative game, and others; see, for example, [3, 4, 19], and the references quoted therein.

Let us denote the set of fixed points of a mapping $T :C \rightarrow C$ by Fix(T); that is, $Fix(T) = \{x \in C:Tx = x\}$. Recall that T is said to be nonexpansive if for all $x, \ y \in C$, $\Vert Tx - Ty\Vert \le \Vert x - y\Vert$. If Fix(T) is nonempty and $\Vert Tx - p \Vert \le \Vert x - p \Vert , \ \forall x \in C, \ p \in Fix(T)$, then T is called quasi-nonexpansive. It is well-known that Fix(T) is closed and convex when T is quasi-nonexpansive [13].

A mapping T is said to be pseudocontractive if for all $x, \ y \in C$ and $\tau > 0$,

$$\begin{aligned} \Vert x - y\Vert \le \Vert (1+\tau )(x - y) - \tau (Tx - Ty)\Vert . \end{aligned}$$

To find a fixed point of a Lipschitzian pseudocontractive map, Ishikawa [12], in 1974, proposed to use the following iteration procedure

$$\begin{aligned} {\left\{ \begin{array}{ll} x^0 \in C,\\ y^k = \alpha _k x^k + (1 - \alpha _k)Tx^k, \\ x^{k+1} = \beta _k x^k + (1 - \beta _k)Ty^k \end{array}\right. } \end{aligned}$$

(2)

where $0 \le \alpha _k \le \beta _k \le 1$ for all k and proved that if $\lim _{k \rightarrow \infty } \beta _k = 1$, $\sum _{k=1}^{\infty }(1 - \alpha _k)(1 - \beta _k) = \infty$, then $\{x^k\}$ generated by (2) converges weakly to a fixed point of mapping T (see [10, 12]).

In 2006, Yanes and Xu [29] introduced the following by combining Ishikawa iteration process with hybrid projection method [20] for a nonexpansive mapping T.

$$\begin{aligned} {\left\{ \begin{array}{ll} x^0 \in C,\\ y^k = \alpha _k x^k + (1 - \alpha _k)Tx^k, \\ z^{k} = \beta _k x^k + (1 - \beta _k)Ty^k,\\ C_k \!= \!\{x \in C\!:\!\Vert x - z^k \Vert ^2 \le \Vert x \!- \!x^k \Vert ^2 \!+\! (1 \!-\! \alpha _k)(\Vert y^k \Vert ^2 - \Vert x^k \Vert ^2 \!+\! 2\langle x^k - y^k, x \rangle ) \},\\ Q_k = \{x \in C:\langle x - x^k , x^0 - x^k \rangle \le 0 \}, \\ x^{k+1} = P_{C_k \cap Q_k} x^0, \end{array}\right. } \end{aligned}$$

(3)

where $\{\alpha _k\}$ and $\{\beta _k\}$ are sequences in [0, 1]. They proved that if $\lim _{k \rightarrow \infty } \alpha _k = 1$ and $\beta _k \le \bar{\beta }$ for some $\bar{\beta } \in [0, 1)$, then $\{x^k\}$ generated by (3) converges strongly to $P_{Fix(T)} (x^0).$

In recent years, many researchers studied the problem of finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a nonexpansive or demicontractive mapping; see, for instance, [2, 5, 17, 21, 28] and the references therein. Remember that a mapping $T :C \rightarrow \mathbb {H}$ is called symmetric generalized hybrid [11, 14, 25] if there exist $\alpha , \beta , \gamma , \delta \in \mathbb {R}$ such that

$$\begin{aligned}&\alpha \Vert Tx - Ty\Vert ^2 + \beta (\Vert x - Ty\Vert ^2 + \Vert y - Tx \Vert ^2 ) + \gamma \Vert x - y\Vert ^2 \\&\quad +\,\delta (\Vert x - Tx\Vert ^2 + \Vert y - Ty \Vert ^2 )\le 0, \quad \forall x, y \in C. \end{aligned}$$

Such a mapping is called an $(\alpha , \beta , \gamma , \delta )$-symmetric generalized hybrid mapping.

For obtaining a common element of the set of solutions of EP(C, f) and fixed points of a symmetric generalized hybrid mapping T, Moradlou and Alizadeh [18] proposed to combine Ishikawa iterative scheme with the hybrid projection method [20, 23, 24]. More precisely, the iterates $x^k, \ y^k, \ u^k,\ z^k$ are calculated as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x^0 \in C,\\ u^k \in C \text { such that } f(u^k, y) + \frac{1}{r_k}\langle y - u^k, u^k - x^k \rangle \ge 0,\quad \forall y \in C,\\ y^k = \alpha _k x^k + (1 - \alpha _k)Tx^k, \\ z^{k} = \beta _k y^k + (1 - \beta _k)Tu^k,\\ C_k = \{x \in C:\Vert x - z^k \Vert \le \Vert x - x^k \Vert \},\\ Q_k = \{x \in C:\langle x - x^k , x^0 - x^k \rangle \le 0 \}, \\ x^{k+1} = P_{C_k \cap Q_k} x^0. \end{array}\right. } \end{aligned}$$

(4)

The authors showed that if $Sol(C, f) \cap Fix(T) \ne \emptyset$, $(\alpha , \ \beta , \ \gamma , \ \delta )$-symmetric generalized hybrid mapping T satisfying $(1) \ \alpha + 2\beta + \gamma \ge 0$, $(2) \ \alpha + \beta > 0$, and $(3) \ \delta \ge 0$, then under certain appropriate conditions imposed on $\{\alpha _k\}$, $\{\beta _k\}$, the sequence $\{x^k\}$ converges strongly to $x^* = P_{Sol(C, f) \cap Fix(T)}(x^0)$ provided that f is monotone on C.

Note that mapping T satisfies the conditions (1)–(3), then T is quasi-nonexpansive and demiclosed at 0.

In this paper, we modify Moradlou and Alizadeh’s iteration process for finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a generalized hybrid mapping in a real Hilbert space in which the bifunction f is pseudomonotone on C with respect to Sol(C, f). More precisely, we propose to use the extragradient algorithm [16] for solving the equilibrium problem (see also [7–9, 15, 26] for more detail extragradient algorithms). One advantage of our algorithm is that it could be applied for the pseudomonotone equilibrium problem case and each iteration we only have to solve two strongly convex optimization problems instead of a regularized equilibrium as in Moradou and Alizaded’s method.

The paper is organized as follows. The next section contains some preliminaries on the metric projection, equilibrium problems and symmetric generalized hybrid mappings. An extragradient algorithm and its convergence is presented in the third section. The last section is devoted to presentation of an extragradient algorithm with linesearch and its convergence.

2 Preliminaries

In the rest of this paper, by $P_C$ we denote the metric projection operator on C, that is

$$\begin{aligned} P_C(x) \in C:\Vert x - P_C(x) \Vert \le \Vert y - x\Vert , \quad \forall y \in C. \end{aligned}$$

The following well known results on the projection operator onto a closed convex set will be used in the sequel.

Lemma 1

Suppose that C is a nonempty closed convex subset in $\mathbb {H}$. Then

• (a) $P_C(x)$ is singleton and well defined for every x;

• (b) $z = P_C(x)$ if and only if $\langle x - z , y - z \rangle \le 0, \forall y \in C;$

• (c) $\Vert P_C(x) - P_C(y)\Vert ^2 \le \Vert x-y\Vert ^2 - \Vert P_C(x) - x + y - P_C(y)\Vert ^2 , \ \forall x, y \in C$.

Lemma 2

[29] Let C be a nonempty closed convex subset of $\mathbb {H}$. Let $\{x^k\}$ be a sequence in $\mathbb {H}$ and $u \in \mathbb {H}$. If any weak limit point of $\{x^k\}$ belongs to C and

$$\begin{aligned} \Vert x^k - u \Vert \le \Vert u - P_C(u)\Vert , \quad \forall k. \end{aligned}$$

Then $x^k \rightarrow P_C(u)$.

Definition 1

A bifunction $\varphi :C \times C \rightarrow \mathbb {R}$ is said to be jointly weakly continuous on $C \times C$ if for all $x, y \in C$ and $\{x^k\}$, $\{y^k\}$ are two sequences in C converging weakly to x and y respectively, then $\varphi (x^k, y^k)$ converges to $\varphi (x, y)$.

In the sequel, we need the following blanket assumptions

• $(A_1)$ f is jointly weakly continuous on $C\times C$;

• $(A_2)$ $f(x, \cdot )$ is convex, lower semicontinuous, and subdifferentiable on C, for all $x\in C$;

• $(A_3)$ f is pseudomonotone on C with respect to Sol(C, f), i.e., $f(x, x^*)\le 0$ for all $x \in C$, $x^* \in Sol(C, f)$;

• $(A_4)$ f is Lipschitz-type continuous on C with constants $L_1 >0$ and $L_2 >0$, i.e.,

  $$\begin{aligned} f(x, y)+f(y, z)\ge f(x, z) - L_1 \Vert x-y \Vert ^2 - L_2 \Vert y-z \Vert ^2, \quad \forall x, y, z\in C; \end{aligned}$$

• $(A_5)$ T is an ($\alpha , \beta , \gamma , \delta$)-symmetric generalized hybrid self-mapping of C such that $(1) \ \alpha + 2\beta + \gamma \ge 0$, $(2) \ \alpha + \beta > 0$, $(3) \ \delta \ge 0$, and Fix(T) is nonempty.

For each $z, \ x \in C$, by $\partial _2 f(z , x)$ we denote the subdifferential of the convex function f(z, .) at x, i.e.,

$$\begin{aligned} \partial _2 f(z , x) := \{ w \in \mathbb {H} :f(z, y) \ge f(z, x) + \langle w, y - x \rangle , \quad \forall y \in C \}. \end{aligned}$$

In particular,

$$\begin{aligned} \partial _2 f(z , z) = \{ w \in \mathbb {H} :f(z, y) \ge \langle w, y - z \rangle , \quad \forall y \in C \}. \end{aligned}$$

Let $\Omega$ be an open convex set containing C. The next lemma can be considered as an infinite-dimensional version of Theorem 24.5 in [22].

Lemma 3

[27, Proposition 4.3] Let $f :\Omega \times \Omega \rightarrow \mathbb {R}$ be a function satisfying conditions $(A_1)$ on $\Omega$ and $(A_2)$ on C. Let $\bar{x}, \bar{y} \in \Omega$ and $\{x^k\}$, $\{y^k\}$ be two sequences in $\Omega$ converging weakly to $\bar{x}, \bar{y}$, respectively. Then, for any $\epsilon > 0$, there exist $\eta >0$ and $k_{\epsilon } \in \mathbb {N}$ such that

$$\begin{aligned} \partial _2 f(x^k, y^k) \subset \partial _2 f(\bar{x}, \bar{y}) + \frac{\epsilon }{\eta }B, \end{aligned}$$

for every $k \ge k_\epsilon$, where B denotes the closed unit ball in $\mathbb {H}.$

Lemma 4

Suppose the bifunction f satisfies the assumptions $(A_1)$ on $\Omega$ and $(A_2)$ on C. If $\{x^k \} \subset C$ is bounded, $\rho > 0$, and $\{y^k\}$ is a sequence such that

$$\begin{aligned} y^k = \arg \min \left\{ f(x^k, y) + \frac{\rho }{2} \Vert y-x^k\Vert ^2:y\in C\right\} , \end{aligned}$$

then $\{y^k\}$ is bounded.

Proof

Firstly, we show that if $\{x^k \}$ converges weakly to $x^*$, then $\{y^k\}$ is bounded. Indeed,

$$\begin{aligned} y^k = \text {arg}\min \left\{ f(x^k, y) + \frac{\rho }{2} \Vert y-x^k\Vert ^2:y\in C \right\} , \end{aligned}$$

and

$$\begin{aligned} f(x^k, x^k) + \frac{\rho }{2} \Vert x^k-x^k\Vert ^2 = 0, \end{aligned}$$

therefore

$$\begin{aligned} f(x^k, y^k) + \frac{\rho }{2} \Vert y^k-x^k\Vert ^2 \le 0, \quad \forall k. \end{aligned}$$

In addition, for all $w^k \in \partial _2 f(x^k, x^k)$ we have

$$\begin{aligned} f(x^k, y^k) + \frac{\rho }{2} \Vert y^k-x^k\Vert ^2 \ge \langle w^k, y^k - x^k \rangle + \frac{\rho }{2} \Vert y^k - x^k\Vert ^2. \end{aligned}$$

This implies $-\Vert w^k\Vert \Vert y^k - x^k \Vert + \frac{\rho }{2} \Vert y^k - x^k\Vert ^2 \le 0$. Hence,

$$\begin{aligned} \Vert y^k - x^k\Vert \le \frac{2}{\rho } \Vert w^k\Vert , \quad \forall k. \end{aligned}$$

Because $\{x^k\}$ converges weakly to $x^*$ and $w^k \in \partial _2f(x^k, x^k)$, by Lemma 3, the sequence $\{w^k\}$ is bounded, combining with the boundedness of $\{x^k\}$, we get $\{y^k\}$ is also bounded.

Now we prove the Lemma 4. Suppose that $\{y^k\}$ is unbounded, i.e., there exists an subsequence $\{y^{k_i}\} \subseteq \{y^k\}$ such that $\lim _{i \rightarrow \infty }\Vert y^{k_i}\Vert = + \infty$. By the boundedness of $\{x^k\}$, it implies $\{x^{k_i}\}$ is also bounded, without loss of generality, we may assume that $\{x^{k_i}\}$ converges weakly to some $x^*$. By the same argument as above, we obtain $\{y^{k_i}\}$ is bounded, which contradicts. Therefore $\{y^k\}$ is bounded. $\square$

Lemma 5

[14] Let C be a nonempty closed convex subset of $\mathbb {H}$. Assume that T is an $(\alpha , \beta , \gamma , \delta )$-symmetric generalized hybrid self-mapping of C such that $Fix(T) \ne \emptyset$ and the conditions $(1) \ \alpha + 2\beta + \gamma \ge 0$, $(2) \ \alpha + \beta > 0$ and $(3) \ \delta \ge 0$ hold. Then T is quasi-nonexpansive.

Lemma 6

[11] Let C be a nonempty closed convex subset of $\mathbb {H}$ . Assume that T is an $(\alpha , \beta , \gamma , \delta )$-symmetric generalized hybrid self-mapping of C such that $Fix(T) \ne \emptyset$ and the conditions $(1) \ \alpha + 2\beta + \gamma \ge 0$, $(2) \ \alpha + \beta > 0$ and $(3) \ \delta \ge 0$ hold. Then $I - T$ is demiclosed at 0, i.e., $x^k \rightharpoonup \bar{x}$ and $x^k - Tx^k \rightarrow 0$ imply $\bar{x} \in Fix(T)$.

3 An extragradient algorithm

Algorithm 1

• Initialization. Pick $x^0 = x^g \in C$, choose parameters $\{ \rho _k \} \subset [ \underline{\rho }, \ \bar{\rho } ]$, with $0 < \underline{\rho } \le \bar{\rho } < \min \{\frac{1}{2L_1}, \frac{1}{2L_2}\}$, $\{ \alpha _k \} \subset [0, 1], \ \lim _{k \rightarrow \infty } \alpha _k = 1$, $\{\beta _k\} \subset [0, \bar{\beta }] \subset [0, 1)$.

• Iteration k ($k = 0, 1, 2, \ldots$). Having $x^k$ do the following steps:

  • Step 1. Solve the successively strongly convex programs

    $$\begin{aligned}&\min \left\{ \rho _k f(x^k, y) + \frac{1}{2} \Vert y-x^k\Vert ^2:y\in C\right\} \quad {CP(x^k)}\\&\min \left\{ \rho _k f(y^k, y) + \frac{1}{2} \Vert y-x^k\Vert ^2:y\in C\right\} \quad CP(y^k, x^k) \end{aligned}$$

    to obtain their unique solutions $y^k$ and $z^k$ respectively.

  • Step 2. Compute

    $$\begin{aligned} t^{k}&= \alpha _k x^k + (1 -\alpha _k) Tx^k,\\ u^{k}&= \beta _k t^k + (1 -\beta _k) Tz^k. \end{aligned}$$

  • Step 3. Define

    $$\begin{aligned} C_k&= \{x \in \mathbb {H}:\Vert x - u^k \Vert \le \Vert x - x^k \Vert \},\\ Q_k&= \{x \in \mathbb {H}:\langle x - x^k , x^g - x^k \rangle \le 0 \}, \\ A_k&= C_k \cap Q_k \cap C. \end{aligned}$$

    Take $x^{k+1} = P_{A_k}(x^g)$, and go to Step 1 with k is replaced by $k +1$.

Before going to prove the convergence of this algorithm, let us recall the following result which was proved in [1]

Lemma 7

[1] Suppose that $x^* \in \text { Sol}(C, f)$, then under assumptions $(A_2)$, $(A_3)$, and $(A_4)$, we have:

• (i) $\rho _k[f(x^k, y)-f(x^k, y^k)] \ge \langle y^k-x^k, y^k-y \rangle ,\;\forall y \in C.$

• (ii) $\Vert z^k-x^* \Vert ^2 \le \Vert x^k-x^* \Vert ^2- (1 - 2\rho _k L_1) \Vert x^k-y^k \Vert ^2 - (1-2 \rho _k L_2) \Vert y^k - z^k \Vert ^2,\;\;\forall k.$

Theorem 1

Suppose that the set $S = Sol(C, f) \cap Fix(T)$ is nonempty. Then under assumptions $(A_1), (A_2), (A_3), (A_4),$ and $(A_5)$ the sequences $\{x^k\}$, $\{y^k\}$, $\{z^k\}$ generated by Algorithm 1 converge strongly to the solution $x^* = P_S(x^g)$.

Proof

Take $q \in \ S$, i.e., $q \in Sol(C, f) \cap Fix(T)$. By definition of $\rho _k$: $0 < \underline{\rho } \le \rho _k \le {\bar{\rho }} < \text {min}\{\frac{1}{2L_1}, \frac{1}{2L_2}\}$, we get from Lemma 7 that

$$\begin{aligned} \Vert z^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(5)

By definition of $t^k$, we have

$$\begin{aligned} \Vert t^k - q\Vert= & {} \Vert \alpha _kx^k + (1 - \alpha _k) Tx^k - q \Vert \\\le & {} \alpha _k\Vert x^k - q\Vert + (1 - \alpha _k)\Vert Tx^k - q \Vert . \end{aligned}$$

Since T is ($\alpha , \beta , \gamma , \delta )$-symmetric generalized hybrid mapping with $\alpha + 2\beta + \gamma \ge 0$, $\alpha + \beta > 0$, $\delta \ge 0$. From Lemma 5 it is quasi-nonexpansive, so

$$\begin{aligned} \Vert t^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(6)

Similarly

$$\begin{aligned} \Vert u^k - q\Vert= & {} \Vert \beta _k t^k + (1 - \beta _k) Tz^k - q \Vert \\\le & {} \beta _k \Vert t^k - q \Vert + (1 - \beta _k) \Vert Tz^k - q \Vert \\\le & {} \beta _k \Vert x^k - q \Vert + (1 - \beta _k) \Vert z^k - q \Vert . \end{aligned}$$

Combining with (5) yields

$$\begin{aligned} \Vert u^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(7)

Next, we show that $S \subset C_k \cap Q_k, \ \forall k.$ Indeed, from (7) it implies that $q \in C_k$, or $S \subset C_k$ for all k. We prove $S \subset Q_k$ by induction. It is clear that $S \subset Q_0.$ If $S \subset Q_k$, i.e., $\langle q - x^k, x^g - x^k \rangle \le 0, \ \forall q \in S.$ Since $x^{k+1} = P_{A_k}(x^g)$ we obtain $\langle x - x^{k+1}, x^g - x^{k+1} \rangle \le 0, \ \forall x \in A_k .$ Especially, $\langle q - x^{k+1}, x^g - x^{k+1} \rangle \le 0, \ \forall q \in S$. So $S \subset C_k \cap Q_k, \ \forall k.$

From definition of $Q_k$, it implies that $x^k = P_{Q_k}(x^g)$, so $\Vert x^k - x^g\Vert \le \Vert x - x^g\Vert , \ \forall x \in Q_k$. In particular

$$\begin{aligned} \Vert x^k - x^g\Vert \le \Vert q - x^g \Vert , \quad \forall k, \quad \forall q \in S. \end{aligned}$$

(8)

Consequently, $\{x^k\}$ is bounded. Combining with (6) and (7), we get $\{t^k\}$, $\{u^k\}$ are also bounded.

In addition,

$$\begin{aligned} \Vert x^{k+1} - x^k \Vert ^2= & {} \Vert x^{k+1} - x^g + x^g - x^k \Vert ^2 \\= & {} \Vert x^{k+1} - x^g \Vert ^2 + \Vert x^g - x^k \Vert ^2 + 2 \langle x^{k+1} - x^g, x^g - x^k \rangle \\= & {} \Vert x^{k+1} - x^g \Vert ^2 - \Vert x^g - x^k \Vert ^2 + 2 \langle x^{k+1} - x^k, x^g - x^k \rangle . \end{aligned}$$

Since $x^{k+1} \in Q_k$, it implies from the above inequality that

$$\begin{aligned} \Vert x^{k+1} - x^k \Vert ^2 \le \Vert x^{k+1} - x^g \Vert ^2 - \Vert x^{k} - x^g \Vert ^2. \end{aligned}$$

(9)

Therefore $\{\Vert x^k - x^g \Vert \}$ is nondecreasing sequence. In view of (8), the limit

$\lim _{k \rightarrow \infty }\Vert x^k - x^g\Vert$ exists. Hence, it also follows from (9) that

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert x^{k+1} - x^k \Vert = 0. \end{aligned}$$

(10)

Because $x^{k+1} \in C_k$, it implies that

$$\begin{aligned} \Vert u^{k} - x^k \Vert\le & {} \Vert u^k - x^{k+1} \Vert + \Vert x^{k+1} - x^k \Vert \\\le & {} 2\Vert x^{k+1} - x^k \Vert , \end{aligned}$$

therefore, we deduce from (10) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert u^k - x^k \Vert = 0. \end{aligned}$$

(11)

Besides that $\lim _{k \rightarrow \infty } \alpha _k = 1$, so

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert t^k - x^k \Vert = \lim _{k \rightarrow \infty } (1 - \alpha _k)\Vert x^k - T x^k \Vert = 0. \end{aligned}$$

(12)

It is clear that

$$\begin{aligned} \Vert u^k - q \Vert ^2= & {} \Vert \beta _k (t^k - q) + (1 - \beta _k) (Tz^k - q) \Vert ^2\\= & {} \beta _k \Vert t^k - q\Vert ^2 + (1 - \beta _k) \Vert Tz^k - q\Vert ^2 - \beta _k(1 - \beta _k) \Vert t^k - Tz^k \Vert ^2 \\\le & {} \beta _k \Vert t^k - q\Vert ^2 + (1 - \beta _k) \Vert Tz^k - q\Vert ^2. \end{aligned}$$

In view of (6), Lemmas 5 and 7, yields

$$\begin{aligned} \Vert u^k - q \Vert ^2\le & {} \Vert x^k - q\Vert ^2 - (1 - \beta _k) [ (1 - 2\rho _k L_1) \Vert x^k-y^k \Vert ^2 \\&- (1-2 \rho _k L_2) \Vert y^k - z^k \Vert ^2 ]. \end{aligned}$$

Hence

$$\begin{aligned}&(1 - \beta _k)[(1 - 2\rho _k L_1) \Vert x^k-y^k \Vert ^2 + (1-2 \rho _k L_2) \Vert y^k - z^k \Vert ^2 ] \nonumber \\&\quad \le \Vert x^k - u^k \Vert [ \Vert x^k - q \Vert + \Vert u^k - q \Vert ]. \end{aligned}$$

(13)

Since $0 < 1 -\bar{\beta } \le 1- \beta _k$; $0 < \underline{\rho } \le \rho _k \le \bar{\rho } < \min \{\frac{1}{2L_1}, \frac{1}{2L_2}\}$, and (11), we get from (13) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert x^k - y^k \Vert= & {} 0. \end{aligned}$$

(14)

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert y^k - z^k \Vert= & {} 0. \end{aligned}$$

(15)

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert x^k - z^k \Vert= & {} 0. \end{aligned}$$

(16)

By definition of $u^k$, we have $(1 - \beta _k) Tz^k = u^k - \beta _k t^k$. Hence

$$\begin{aligned} (1 - \bar{\beta }) \Vert Tz^k - z^k \Vert\le & {} \Vert (1- \beta _k) Tz^k - (1 - \beta _k)z^k \Vert \\= & {} \Vert u^k - z^k - \beta _k(t^k - z^k)\Vert \\\le & {} \Vert u^k - z^k \Vert + \beta _k\Vert t^k - z^k\Vert \\\le & {} \Vert u^k - x^k \Vert + \beta _k\Vert t^k - x^k\Vert + (1 + \beta _k) \Vert x^k - z^k\Vert . \end{aligned}$$

Combining this fact with (11), (12), and (16) we receive in the limit that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert Tz^k - z^k \Vert = 0. \end{aligned}$$

(17)

Next we show that any weak accumulation point of $\{x^k\}$ belongs to S. Indeed, suppose that $\{x^{k_i}\} \subset \{x^k\}$ and $x^{k_i} \rightharpoonup p$ as $i \rightarrow \infty$. From (14), (15), and (16) we get $y^{k_i} \rightharpoonup p$, and $z^{k_i} \rightharpoonup p$ as $i \rightarrow \infty$. Replacing k by $k_i$ in assertion (i) of Lemma 7 we get

$$\begin{aligned} \rho _{k_i}[ f(x^{k_i}, y) - f(x^{k_i}, y^{k_i}) ] \ge \langle x^{k_i} - y^{k_i} , y - y^{k_i} \rangle , \quad \forall y \in C. \end{aligned}$$

Hence

$$\begin{aligned} \rho _{k_i}[ f(x^{k_i}, y) - f(x^{k_i}, y^{k_i}) ] \ge -\Vert x^{k_i} - y^{k_i}\Vert \Vert y - y^{k_i}\Vert . \end{aligned}$$

(18)

Letting $i \rightarrow \infty$, by jointly weak continuity of f and (14), we obtain in the limit from (18) that

$$\begin{aligned} f(p, y) - f(p, p) \ge 0. \end{aligned}$$

So

$$\begin{aligned} f(p,y) \ge 0, \quad \forall y \in C, \end{aligned}$$

which means that p is a solution of EP(C, f).

By (17), we have that $\lim _{i \rightarrow \infty }\Vert Tz^{k_i} - z^{k_i}\Vert = 0$. Since $z^{k_i} \rightharpoonup p$ and demiclosedness at zero of $I - T$, Lemma 6, we get $Tp = p$, i.e., $p \in Fix(T).$

Hence $p \in S$.

Now, we set $x^* = P_{S}(x^g)$. From (8) one has,

$$\begin{aligned} \Vert x^k - x^g\Vert \le \Vert x^* - x^g\Vert , \quad \forall k. \end{aligned}$$

It is immediate from Lemma 2 that $x^k$ converges strongly to $x^*$. Combining with (14) and (16) we have that $y^k$, $z^k$ converge strongly to $x^*.$ This completes the proof. $\square$

4 An extragradient algorithm with linesearch

Algorithm 2

• Initialization. Pick $x^0 = x^g \in C$, choose parameters $\eta , \mu \in (0, 1); \ 0 < \underline{\rho } \le \bar{\rho }$, $\{ \rho _k \} \subset [ \underline{\rho }, \ \bar{\rho }]$; $\{ \alpha _k \} \subset [0, 1],$ $\lim _{k \rightarrow \infty } \alpha _k = 1$; $\{\beta _k\} \subset [0, \bar{\beta }] \subset [0, 1)$; $\gamma _k \in [\underline{\gamma }, \bar{\gamma }] \subset (0, 2)$.

• Iteration k $(k = 0, 1, 2, \ldots )$. Having $x^k$ do the following steps:

  • Step 1. Solve the strongly convex program

    $$\begin{aligned} \min \left\{ \rho _k f(x^k, y) + \frac{1}{2} \Vert y-x^k\Vert ^2:y\in C\right\} \quad {CP(x^k)} \end{aligned}$$

    to obtain its unique solutions $y^k$. If $y^k = x^k$, then set $v^k = x^k$. Otherwise go to Step 2.

  • Step 2. (Armijo linesearch rule) Find $m_k$ as the smallest positive integer number m such that

    $$\begin{aligned} {\left\{ \begin{array}{ll} z^{k,m} = (1 - \eta ^m)x^k + \eta ^my^m \\ f(z^{k,m}, x^k) - f(z^{k,m}, y^k) \ge \frac{\mu }{2 \rho _k}\Vert x^k - y^k\Vert ^2. \end{array}\right. } \end{aligned}$$

    (19)

    Set $\eta _k = \eta ^{m_k}$, $z^k = z^{k, m_k}$.

  • Step 3. Select $w^k \in \partial _2f(z^k, x^k)$, and compute $v^k = P_C(x^k - \gamma _k.\sigma _k.w^k)$, where $\sigma _k = \frac{f(z^k, x^k)}{\Vert w^k\Vert ^2}$.

  • Step 4. Compute

    $$\begin{aligned} t^{k}&= \alpha _k x^k + (1 -\alpha _k) Tx^k,\\ u^{k}&= \beta _k t^k + (1 -\beta _k) Tv^k. \end{aligned}$$

  • Step 5. Define

    $$\begin{aligned} C_k&= \{x \in \mathbb {H}:\Vert x - u^k \Vert \le \Vert x - x^k \Vert \},\\ Q_k&= \{x \in \mathbb {H}:\langle x - x^k , x^g - x^k \rangle \le 0 \}, \\ A_k&= C_k \cap Q_k \cap C. \end{aligned}$$

    Take $x^{k+1} = P_{A_k}(x^g)$, and go to Step 1 with k is replaced by $k +1$.

Remark 1

• (i) If $y^k = x^k$ then $x^k$ is a solution to EP(C, f);

• (ii) If $y^k = x^k = t^k$ and $\alpha _k < 1$ or $y^k = x^k = u^k$, then $x^k \in Sol(C, f) \cap Fix(T)$.

Firstly, let us recall the following lemma which was proved in [26]

Lemma 8

[26] Suppose that $p \in \text { Sol}(C, f)$, then under assumptions $(A_2)$, $(A_3)$, and $(A_4)$, we have:

• (a) The linesearch is well defined;

• (b) $f(z^k, x^k) > 0$;

• (c) $0 \not \in \partial _2f(z^k, x^k)$;

• (d)
  $$\begin{aligned} \Vert v^k - p\Vert ^2 \le \Vert x^k - p\Vert ^2 - \gamma _k( 2 - \gamma _k)(\sigma _k\Vert w^k\Vert )^2. \end{aligned}$$

  (20)

Theorem 2

Suppose that the set $S = Sol(C, f) \cap Fix(T)$ is nonempty, the bifunction f satisfies assumptions $(A_1)$ on $\Omega$, $(A_2)$, and $(A_3)$ on C, the mapping T satisfies assumption $(A_5)$. Then the sequences $\{x^k\}$, $\{u^k\}$ generated by Algorithm 2 converge strongly to the solution $x^* = P_S(x^g)$.

Proof

Take $q \in S$. Since $\gamma _k \in [\underline{\gamma }, \bar{\gamma }] \subset (0, 2)$, we get from Lemma 8 that

$$\begin{aligned} \Vert v^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(21)

By definition of $t^k$, we have

$$\begin{aligned} \Vert t^k - q\Vert ^2= & {} \Vert \alpha _k(x^k - q) + (1 - \alpha _k) (Tx^k - q) \Vert ^2 \\= & {} \alpha _k\Vert x^k - q\Vert ^2 + (1 - \alpha _k)\Vert Tx^k - q \Vert ^2 - \alpha _k(1 - \alpha _k)\Vert Tx^k - x^k \Vert ^2. \end{aligned}$$

Since T is a ($\alpha , \beta , \gamma , \delta )$-symmetric generalized hybrid mapping with $\alpha + 2\beta + \gamma \ge 0$, $\alpha + \beta > 0$, $\delta \ge 0$. By Lemma 5 it is quasi-nonexpansive, so

$$\begin{aligned} \Vert t^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(22)

Similarly,

$$\begin{aligned} \Vert u^k - q \Vert \le \Vert x^k - q \Vert . \end{aligned}$$

(23)

Next, we show that $S \subset C_k \cap Q_k, \ \forall k.$ Indeed, from (23) it implies that $q \in C_k$, or $S \subset C_k$. We prove $S \subset Q_k$ by induction, it is clear that $S \subset Q_0.$ If $S \subset Q_k$, i.e., $\langle q - x^k, x^g - x^k \rangle \le 0, \ \forall q \in S.$ Since $x^{k+1} = P_{A_k}(x^g)$ we obtain $\langle x - x^{k+1}, x^g - x^{k+1} \rangle \le 0, \ \forall x \in A_k .$ Especially, $\langle q - x^{k+1}, x^g - x^{k+1} \rangle \le 0, \ \forall q \in S$. So $S \subset C_k \cap Q_k, \ \forall k.$

From definition of $Q_k$, it implies that $x^k = P_{Q_k}(x^g)$, so $\Vert x^k - x^g\Vert \le \Vert x - x^g\Vert , \ \forall x \in Q_k$. In particular

$$\begin{aligned} \Vert x^k - x^g\Vert \le \Vert q - x^g \Vert , \quad \forall k, \quad \forall q \in S. \end{aligned}$$

(24)

Consequently, $\{x^k\}$ is bounded. Combining with (22) and (23), we get $\{t^k\}$, $\{u^k\}$ are also bounded.

In addition,

$$\begin{aligned} \Vert x^{k+1} - x^k \Vert ^2= & {} \Vert x^{k+1} - x^g + x^g - x^k \Vert ^2 \\= & {} \Vert x^{k+1} - x^g \Vert ^2 + \Vert x^g - x^k \Vert ^2 + 2 \langle x^{k+1} - x^g, x^g - x^k \rangle \\= & {} \Vert x^{k+1} - x^g \Vert ^2 - \Vert x^g - x^k \Vert ^2 + 2 \langle x^{k+1} - x^k, x^g - x^k \rangle . \end{aligned}$$

Since $x^{k+1} \in Q_k$, it implies from the above inequality that

$$\begin{aligned} \Vert x^{k+1} - x^k \Vert ^2 \le \Vert x^{k+1} - x^g \Vert ^2 - \Vert x^{k} - x^g \Vert ^2. \end{aligned}$$

(25)

Therefore $\{\Vert x^k - x^g \Vert \}$ is nondecreasing sequence. Together with (24), the limit $\lim _{k \rightarrow \infty }\Vert x^k - x^g\Vert$ does exist.

Hence, it also follows from (25) that

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert x^{k+1} - x^k \Vert = 0. \end{aligned}$$

(26)

Because $x^{k+1} \in C_k$, it implies that

$$\begin{aligned} \Vert u^{k} - x^k \Vert\le & {} \Vert u^k - x^{k+1} \Vert + \Vert x^{k+1} - x^k \Vert \\\le & {} 2\Vert x^{k+1} - x^k \Vert , \end{aligned}$$

therefore, we deduce from (26) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert u^k - x^k \Vert = 0. \end{aligned}$$

(27)

Besides that $\lim _{k \rightarrow \infty } \alpha _k = 1$, so

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert t^k - x^k \Vert = \lim _{k \rightarrow \infty } (1 - \alpha _k)\Vert x^k - T x^k \Vert = 0. \end{aligned}$$

(28)

It is clear that

$$\begin{aligned} \Vert u^k - q \Vert ^2= & {} \Vert \beta _k (t^k - q) + (1 - \beta _k) (Tv^k - q) \Vert ^2\\= & {} \beta _k \Vert t^k - q\Vert ^2 + (1 - \beta _k) \Vert Tv^k - q\Vert ^2 - \beta _k(1 - \beta _k) \Vert t^k - Tv^k \Vert ^2 \\\le & {} \beta _k \Vert t^k - q\Vert ^2 + (1 - \beta _k) \Vert Tv^k - q\Vert ^2. \end{aligned}$$

In view of (22) and Lemma 8, yields

$$\begin{aligned} \Vert u^k - q \Vert ^2 \le \Vert x^k - q\Vert ^2 - (1 - \beta _k) \gamma _k(2 - \gamma _k)(\sigma _k \Vert w^k\Vert )^2. \end{aligned}$$

Hence

$$\begin{aligned} (1 - \beta _k) \gamma _k(2 - \gamma _k)(\sigma _k \Vert w^k\Vert )^2 \le \Vert x^k - u^k \Vert [ \Vert x^k - q \Vert + \Vert u^k - q \Vert ]. \end{aligned}$$

(29)

Since $0 < 1 -\bar{\beta } \le 1- \beta _k$; $\gamma _k \in [\underline{\gamma }, \bar{\gamma }] \subset (0, 2)$, and (27), we get from (29) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \sigma _k\Vert w^k \Vert = 0. \end{aligned}$$

(30)

Because $v^k = P_C(x^k - \gamma _k\sigma _k w^k)$, one has

$$\begin{aligned} \Vert v^k - x^k\Vert \le \gamma _k\sigma _k \Vert w^k\Vert . \end{aligned}$$

Combining with (30) we get

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert v^k - x^k \Vert = 0. \end{aligned}$$

(31)

By definition of $u^k$, we have $(1 - \beta _k) Tv^k = u^k - \beta _k t^k$. Hence

$$\begin{aligned} (1 - \bar{\beta }) \Vert Tv^k - v^k \Vert\le & {} \Vert (1- \beta _k) Tv^k - (1 - \beta _k)v^k \Vert \\= & {} \Vert u^k - v^k - \beta _k(t^k - v^k)\Vert \\\le & {} \Vert u^k - v^k \Vert + \beta _k\Vert t^k - v^k\Vert \\\le & {} \Vert u^k - x^k \Vert + \beta _k\Vert t^k - x^k\Vert + (1 + \beta _k) \Vert x^k - v^k\Vert . \end{aligned}$$

Combining this fact with (27), (28), and (31), we receive in the limit that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert Tv^k - v^k \Vert = 0. \end{aligned}$$

(32)

By Lemma 4, $\{y^k\}$ is bounded, consequently $\{z^k\}$ is bounded. From Lemma 3, $\{w^k\}$ is bounded. In view of ( 30) yields

$$\begin{aligned} \lim _{k \rightarrow \infty } f(z^k, x^k) = \lim _{k \rightarrow \infty } [\sigma _k\Vert w^k\Vert ] \Vert w^k\Vert = 0. \end{aligned}$$

(33)

We have

$$\begin{aligned} 0 = f(z^k, z^k)= & {} f(z^k, (1 - \eta _{k}) x^k + \eta _k y^k) \\\le & {} (1 - \eta _k)f(z^k, x^k) + \eta _k f(z^k, y^k), \end{aligned}$$

so, we get from (19) that

$$\begin{aligned} f(z^k, x^k)\ge & {} \eta _k [f(z^k, x^k) - f(z^k, y^k)]\\\ge & {} \frac{\mu }{2\rho _k} \eta _k \Vert x^k - y^k \Vert ^2. \end{aligned}$$

Combining with (33) one has

$$\begin{aligned} \lim _{k \rightarrow \infty } \eta _k\Vert x^k - y^k\Vert ^2 = 0. \end{aligned}$$

(34)

Next, we show that any weak accumulation point of $\{x^k\}$ belongs to S. Indeed, suppose that $\{x^{k_i}\} \subset \{x^k\}$ and $x^{k_i} \rightharpoonup p$ as $i \rightarrow \infty$.

From (34) we get

$$\begin{aligned} \lim _{i \rightarrow \infty } \eta _{k_i}\Vert x^{k_i} - y^{k_i}\Vert ^2 = 0. \end{aligned}$$

(35)

We now consider two distinct cases:

Case 1. $\lim \sup _{i \rightarrow \infty }\eta _{k_i} > 0$.

Without loss of generality, we may assume that there exists $\bar{\eta } > 0$ such that $\eta _{{k}_i} > \bar{\eta }, \ \forall i \ge i_0$, use this fact and from (35), one has

$$\begin{aligned} \lim _{i \rightarrow \infty }{\Vert x^{{k}_i}-y^{{k}_i}\Vert } = 0. \end{aligned}$$

(36)

Remember that $x^k \rightharpoonup p$, together with (36), it implies that $y^{k_i} \rightharpoonup p$ as $i \rightarrow \infty$.

From assertation (i) of Lemma 7 we get

$$\begin{aligned} \rho _{k_i}[ f(x^{k_i}, y) - f(x^{k_i}, y^{k_i}) ] \ge \langle x^{k_i} - y^{k_i} , y - y^{k_i} \rangle , \quad \forall y \in C. \end{aligned}$$

Hence

$$\begin{aligned} \rho _{k_i}[ f(x^{k_i}, y) - f(x^{k_i}, y^{k_i}) ] \ge -\Vert x^{k_i} - y^{k_i}\Vert \Vert y - y^{k_i}\Vert . \end{aligned}$$

(37)

Letting $i \rightarrow \infty$, by jointly weak continuity of f and (36), we obtain in the limit from (37) that

$$\begin{aligned} f(p, y) - f(p, p) \ge 0. \end{aligned}$$

So

$$\begin{aligned} f(p,y) \ge 0, \quad \forall y \in C, \end{aligned}$$

which means that p is a solution of EP(C, f).

Case 2. $\lim _{i \rightarrow \infty }{\eta _{k_i}} = 0$.

From the boundedness of $\{y^{k_i}\}$, without loss of generality we may assume that $y^{k_i} \rightharpoonup \bar{y}$ as $i \rightarrow \infty$.

Replacing y by $x^{k_i}$ in (i) of Lemma 7 we get

$$\begin{aligned} f(x^{k_i}, y^{k_i}) \le -\frac{1}{\rho _{k_i}} \Vert y^{k_i} - x^{k_i} \Vert ^2. \end{aligned}$$

(38)

In the other hand, by the Armijo linesearch rule (19), for $m_{k_i} - 1$, we have

$$\begin{aligned} f(z^{k_i, m_{k_i} - 1}, x^{k_i}) - f(z^{k_i, m_{k_i} - 1}, y^{k_i}) < \frac{\mu }{2\rho _{k_i}} \Vert y^{k_i}-x^{k_i}\Vert ^2. \end{aligned}$$

(39)

Combining with (38) we get

$$\begin{aligned} f(x^{k_i}, y^{k_i}) \le -\frac{1}{\rho _{k_i}} \Vert y^{k_i} - x^{k_i} \Vert ^2 \le \frac{2}{\mu } [f(z^{k_i, m_{k_i} - 1}, y^{k_i}) - f(z^{k_i, m_{k_i} - 1}, x^{k_i}) ].\nonumber \\ \end{aligned}$$

(40)

According to the algorithm, we have $z^{k_i, m_{k_i} - 1} = (1-\eta ^{m_{k_i} - 1})x^{k_i} + \eta ^{m_{k_i} - 1}y^{k_i}$, $\eta ^{k_i, m_{k_i} - 1} \rightarrow 0$ and $x^{k_i}$ converges weakly to p, $y^{k_i}$ converges weakly to $\bar{y}$, it implies that $z^{k_i, m_{k_i} - 1} \rightharpoonup p$ as $i \rightarrow \infty$. Beside that $\{\frac{1}{\rho _{k_i}}\Vert y^{k_i} - x^{k_i}\Vert ^2\}$ is bounded, without loss of generality, we may assume that $\lim _{i \rightarrow +\infty }\frac{1}{\rho _{k_i}}\Vert y^{k_i} - x^{k_i}\Vert ^2$ exists. Hence, we get in the limit from (40) that

$$\begin{aligned} f(p, \bar{y}) \le - \lim _{i \rightarrow +\infty }\frac{1}{\rho _{k_i}}\Vert y^{k_i} - x^{k_i}\Vert ^2 \le \frac{2}{\mu }f(p, \bar{y}). \end{aligned}$$

Therefore, $f(p, \bar{y}) = 0$ and $\lim _{i \rightarrow +\infty }\Vert y^{k_i} - x^{k_i}\Vert ^2 = 0$. By the Case 1, it is immediate that p is a solution of EP(C, f).

In addition, from (31) and (32), we have $v^{k_i} \rightharpoonup p$ and $\lim _{i \rightarrow \infty }\Vert Tv^{k_i} - v^{k_i}\Vert = 0$. By Lemma 6, $I - T$ is demiclosed at zero, we get $Tp = p$, i.e., $p \in Fix(T)$.

Hence $p \in S$.

Now, we set $x^* = P_{S}(x^g)$. From (24) one has,

$$\begin{aligned} \Vert x^k - x^g\Vert \le \Vert x^* - x^g\Vert , \quad \forall k. \end{aligned}$$

(41)

We get from Lemma 2 that $x^k$ converges strongly to $x^*$. Combining with (27) we also have that $u^k$ converges strongly to $x^*.$ The proof is completed. $\square$

An example and preliminary computational results. To illustrate the proposed algorithms, we consider a problem when the bifunction f and the mapping T are given as follows

$$\begin{aligned} f(x,y)&= (Px + Qy +r)^T(y - x), \\ Tx&= (I + U)^{-1}x, \end{aligned}$$

where $P = (p_{ij})_{n \times n}$, $Q = (q_{ij})_{n \times n}$, $U = (u_{ij})_{n \times n}$ are $n \times n$ symmetric positive semidefinite matrices such that $P-Q$ is also positive semidefinite and $r \in \mathbb {R}^n.$ The bifunction f has the form of the one arising from a Nash-Cournot oligopolistic electricity market equilibrium model [6] and that f is convex in y, Lipschitz-type continuous with constants $L_1 = L_2 = \frac{1}{2}\Vert P-Q\Vert$, and the positive semidefinition of $P-Q$ implies that f is monotone [26]. It is clear that the set of fixed points of mapping T is the solution set of the equation $Ux = 0.$ In order to ensure that the intersection of the solution set of EP(C, f) and the fixed points of the mapping T is nonempty, we futher assume that the constraint set C contains the original, $r = 0,$ and U is a diagonal matrix such that $u_{ii} > 0$, forall $i \in I_0$ and $u_{ii} = 0$, forall $i \not \in I_0$, for some index set $I_0 \subset \{1, 2, \ldots , n-1, n \}.$

We tested the proposed algorithms for this example in which C is the box $C = \prod _{i=1}^{n}[-10, 10],$ $P, \ Q, \ U$ are matrices of the form $A^TA$ with $A = (a_{ij})_{n \times n}$ being randomly generated in the interval $[-5, 5]$, starting point $x^g$ is randomly generated in $[-10, 10]$ and the parameters: $\alpha _0 = \beta _0 = \frac{1}{2}, \alpha _k = 1 - \frac{1}{k+2}, \beta _k = \frac{1}{2} + \frac{1}{k+3}$, and $\rho _k = \frac{0.5}{\Vert P - Q\Vert }$ in Algorithm 1; $\eta = 0.98$, $\mu = 0.4$, $\rho _k = 0.5, \gamma _k = 1$ in Algorithm 2.

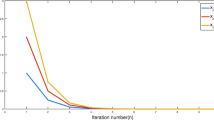
We implement Algorithms 1 and 2 for this problem in Matlab R2013 running on a Desktop with Intel(R) Core(TM) 2Duo CPU E8400 3 GHz, and 3 GB RAM. To terminate the algorithms, we use the stopping criteria $\Vert x^{k+1} - x^k\Vert < \epsilon$ with a tolerance $\epsilon = 0.01$.

The computation results on Algorithms 1 and 2 are reported in Tables 1 and 2 respectively, where

• N.P: the number of the tested problems;

• average times: the average CPU-computation times (in s);

• average iteration: the average number of iterations.

Table 1 Results computed with Algorithm 1

Table 2 Results computed with Algorithm 2

From the computed results reported in these tables, we can see that the computational time by Algorithm 1 is less than that by Algorithm 2, probably due to Lipschitz type condition of bifunction f and the parameters $\rho _k$ is defined by f in each problem.

5 Conclusion

We have introduced two iterative methods for finding a common point of the solution set of a pseudomonotone equilibrium problem and the set of fixed points of a symmetric generalized hybrid mapping in a real Hilbert space. The basic iteration used in this paper is the extragradient iteration with or without the incorporation of a linesearch procedure. The strong convergence of the iterates has been obtained.