1 Introduction

Malaria is an infectious disease of humans, usually transmitted through the bites of Anopheline mosquitoes. Female mosquitoes bite humans (and other warm-blooded animals) for blood meals to provide protein for egg development. During each feed, the mosquito injects some saliva into the host to prevent clotting before sucking the blood into its stomach. After ingesting the blood, the mosquito rests for two to three days (depending on the ambient temperature) while it digests the blood. The mosquito then searches for a water body where it lays the eggs and then seeks another host to repeat its feeding cycle [23].

Mosquitoes experience different levels of mortality risk during the different phases of the feeding cycle. Host-seeking and attempting to feed on hosts is the most dangerous part of the cycle, where mosquitoes are most likely to die. The resting phase is usually the safest where mosquitoes are stationary. However, the mortality risks of the different stages can be altered by malaria control interventions. For example, insecticide-treated nets increase the mortality of host-seeking mosquitoes and indoor residual spraying with insecticides increases the mortality of resting mosquitoes [12].

Infectious mosquitoes contain malaria sporozoites in their salivary glands and infect humans when they inject saliva into them. In humans, the sporozoites pass through liver and asexual blood stages before transforming into infective sexual stages (called gametocytes). The incubation period in humans is relatively short (about 20 days) but the infectious period can last for multiple months. Humans infect mosquitoes when a mosquito sucks up a male and a female gametocyte during her blood meal. The gametocytes then fuse in the mosquito’s stomach to eventually form an oocyst that releases sporozoites (that then travel to the mosquito’s salivary glands to complete the malaria life cycle). The incubation period in the mosquito is about 10–12 days long, which is on the same order as the mosquito’s life span so it has a substantial effect on malaria epidemiology and control [16].

Recent evidence has shown that malaria parasites can affect the mosquito’s host-seeking behaviour to increase their probability of transmission [1, 19, 20]. Mosquitoes with oocysts (who are infected but not yet infectious) tend to be less mobile and spend more time resting. They therefore have longer feeding cycles and experience a lower mortality rate than uninfected mosquitoes. Mosquitoes with sporozoites tend to be more restless and are likely to take multiple blood meals in a single feeding cycle (that is, they bite multiple hosts before resting). Therefore, although they experience a higher mortality rate than uninfected mosquitoes, they also feed more frequently and thereby infect humans more often than they would if their feeding rate was unchanged.

Additionally, there is evidence that humans with a high density of gametocytes are more attractive to mosquitoes than humans without gametocytes [21], thereby making it easier for infectious humans to transmit to mosquitoes.

There is a long history of mathematical models of malaria starting with Ronald Ross’ first ordinary differential equation (ODE) model for the proportion of infectious humans and mosquitoes [26]. Most models developed since then have been similar deterministic population-based models [2, 3, 10, 24, 25] although recently stochastic individual-based simulation models have increased in prominence [17, 28]. However, these models have rarely considered the impact of malaria infection in mosquitoes on their feeding frequency or the impact of malaria infection in humans on their attractiveness to mosquitoes.

Here we develop a simple deterministic population-based model that extends existing models to include these effects. We first describe the model and perform a qualitative analysis to show the existence of disease-free and endemic equilibrium points, and the possibility of a backward transcritical bifurcation that is common to many such malaria models. We finally perform some numerical simulations that illustrate the effects of varying the infection-state dependent mosquito biting frequency and the relative attractiveness of infectious humans.

2 The model

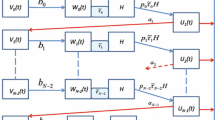
We assume that the mosquito population is divided into three disjoint compartments: susceptible, exposed (mosquitoes carrying oocysts), and infectious (mosquitoes carrying malaria sporozoites). We denote the three populations at time t as \(S_v(t)\), \(E_v(t)\) and \(I_v(t)\), respectively. In order to account for the effects of malaria parasites on the mosquito’s host-seeking behaviour [1, 19, 20], we introduce two positive constants, \(\varphi _E\), and \(\varphi _I\), to represent the biting rate of exposed and infectious mosquitoes relative to susceptible mosquitoes, with \(\varphi _E <1\) and \(\varphi _I >1\).

Furthermore, by using the modelling approach employed first in [9] and later in [4–6, 29], we divide humans into two compartments: susceptible, \(S_h(t)\), who are not infected with malaria, and infectious, \(I_h(t)\), who carry gametocytes. We denote the increased relative attractiveness of infectious humans as compared to susceptible humans (vector-bias parameter) by p. For simplicity, we assume that humans infected with malaria are always infectious; thus ignoring the incubation period and any variations in gametocyte density over time.

Table 1 Description and baseline values/range of parameters of model (1)
Full size table

The balance equations lead to the following system of nonlinear ODES,

$$\begin{aligned} \dot{S_h}&= \Lambda _h - \lambda _h(t) S_h - \mu S_h + \delta I_h, \end{aligned}$$
(1a)
$$\begin{aligned} \dot{I_h}&= \lambda _h(t) S_h - (\alpha + \mu + \delta ) I_h, \end{aligned}$$
(1b)
$$\begin{aligned} \dot{S_v}&= \Lambda _v - \lambda _v(t) S_v - \eta S_v, \end{aligned}$$
(1c)
$$\begin{aligned} \dot{E_v}&= \lambda _v(t) S_v - (\varphi _E \eta + \gamma ) E_v, \end{aligned}$$
(1d)
$$\begin{aligned} \dot{I_v}&= \gamma E_v - \varphi _I \eta I_v, \end{aligned}$$
(1e)

where the upper dots denote the time derivative. The terms \(\lambda _h(t)\) and \(\lambda _v(t)\) denote the forces of infection on humans and vectors, respectively. The infection rate per susceptible human and per susceptible vector are given, respectively, by,

$$\begin{aligned} \lambda _h(t)&= \varphi _I \omega \pi _h \frac{I_v}{p I_h + S_h}, \end{aligned}$$
(2a)
$$\begin{aligned} \lambda _v(t)&= \omega \pi _m \frac{p I_h}{p I_h + S_h}. \end{aligned}$$
(2b)

The description and the baseline values of the parameters in (1) and (2) are given in Table 1.

Denoting by \(N_h\) the total human population and by \(N_v\) the total vector population, i.e., \(N_h=S_h+I_h\), and \(N_v=S_v+E_v+I_v\), it easily follows that the feasible region for model (1) is

$$\begin{aligned} \mathcal {D}=\left\{ (S_h,I_h,S_v,E_v,I_v)\in {\bar{\mathbb {R}}}^{5}_{+}:\; N_h\le \frac{\Lambda _h}{\mu },\;\;\;N_v\le \frac{\Lambda _v}{\varphi _E\eta } \right\} , \end{aligned}$$

where \(\bar{\mathbb {R}}_+^n\) denotes the non-negative orthant of \(\mathbb {R}^n\).

3 Local stability analysis of the disease-free equilibrium point

It is easy to check that model (1) admits the disease-free equilibrium (DFE) given by

$$\begin{aligned} E_0\equiv \left( S_{h}^{0},0,0,S_v^0,0\right) = \left( \frac{\Lambda _h}{\mu },0,0,\frac{\Lambda _v}{\eta },0\right) . \end{aligned}$$
(3)

We use the next generation matrix method [13, 14] to derive the basic reproduction number \(R_0\). The ‘infected’ compartments of model (1) are \(I_h\), \(E_v\) and \(I_v\). The ‘new infection’ matrix F and the ‘transition’ matrix V defined in [14] are given, respectively, by

$$\begin{aligned} F=\begin{pmatrix} 0\;\; &{}\quad 0\;\; &{}\quad \pi _{h}\omega \varphi _{I} \\ \dfrac{\pi _{m}\,\omega \,p\,S^{0}_{v}}{S^{0}_{h}} \;\; &{}\quad 0 \;\; &{}\quad 0 \\ 0 \;\; &{}\quad 0 \;\; &{}\quad 0 \\ \end{pmatrix} \quad \text { and }\quad V=\begin{pmatrix} \mu +\alpha +\delta &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \varphi _E \eta + \gamma &{}\quad 0 \\ 0 &{}\quad -\gamma &{}\quad \eta \,\varphi _{I} \\ \end{pmatrix}. \end{aligned}$$

The the basic reproduction number is the dominant eigenvalue of the next generation matrix \(FV^{-1}\),

$$\begin{aligned} R_0=\rho (FV^{-1})=\sqrt{\dfrac{\omega ^{2}\pi _h\pi _m p\gamma \mu \Lambda _v}{(\mu +\alpha +\delta )(\varphi _E\eta +\gamma )\eta ^{2}\Lambda _h}}. \end{aligned}$$
(4)

Theorem 1

The disease-free equilibrium \(E_0\), given by (3), is locally asymptotically stable if \(R_0 <1\) and unstable if \(R_0 >1\), where \(R_0\) is given by (4).

This theorem follows from a straightforward application of Theorem 2 in [14] and showing that the model equations satisfy the five assumptions (A1)–(A5) in [14]. We note that the basic reproduction number may be written as \(R_0=\sqrt{K_h\,K_v}\), where:

$$\begin{aligned} K_h=(\omega )\left( \frac{\mu \Lambda _v}{\eta \Lambda _h}\right) (p)(\pi _m) \left( \frac{1}{\mu +\alpha +\delta }\right) , \end{aligned}$$

and

$$\begin{aligned} K_v=(\varphi _I \omega )(\pi _h) \left( \frac{1}{\varphi _I \eta }\right) \left( \frac{\gamma }{\varphi _E\eta +\gamma }\right) . \end{aligned}$$

The quantity \(K_h\) is the number of mosquitoes infected by one human during his/her infectious life time. It is the product of the biting rate of a susceptible mosquito, the ratio of mosquitoes to humans at the disease-free equilibrium, the vector-bias parameter, the probability of disease transmission from infectious humans to susceptible mosquito per bite, and the average infectious period in humans. The quantity \(K_v\) is the number of humans infected by one mosquito during her infectious life time. It is the product of the biting rate of infectious mosquitoes, the probability of disease transmission from infectious mosquito to susceptible human per bite, the average duration of the infectious period in mosquitoes, and the probability that a mosquito survives the exposed period. The basic reproduction number \(R_0\) is the geometric mean of \(K_h\) and \(K_v\) since the infection from human to human goes through one generation of mosquitoes. We note that the increased frequency of biting of infectious, \(\varphi _I\), cancels out in \(K_v\) so it does not influence \(R_0\).

4 Endemic equilibrium points

By endemic, we mean an equilibrium of system (1) where all components are positive. The components are solutions of the following system,

$$\begin{aligned} \Lambda _h - \lambda _h S_h - \mu S_h + \delta I_h&=0, \end{aligned}$$
(5a)
$$\begin{aligned} \lambda _h S_h - (\alpha + \mu + \delta ) I_h&=0, \end{aligned}$$
(5b)
$$\begin{aligned} \Lambda _v - \lambda _v S_v - \eta S_v&=0, \end{aligned}$$
(5c)
$$\begin{aligned} \lambda _v S_v - (\varphi _E \eta + \gamma ) E_v&=0, \end{aligned}$$
(5d)
$$\begin{aligned} \gamma E_v - \varphi _I \eta I_v&=0. \end{aligned}$$
(5e)

We let \(E=\left( S^{*}_h,I^{*}_h,S^{*}_v,E^{*}_v,I^{*}_v\right) \) represent any generic endemic equilibrium point of (1) and let

$$\begin{aligned} \lambda ^{*}_h=\varphi _I\omega \pi _h\frac{I^{*}_v}{p I^{*}_h+S_{h}^{*}}\quad \text { and }\quad \lambda ^{*}_v=\omega \pi _m p\frac{I^{*}_h}{p I^{*}_h+S_{h}^{*}}, \end{aligned}$$
(6)

be the forces of infection of humans and vectors at steady state, respectively. Solving equations (5) for the state variables provides

$$\begin{aligned} S^{*}_h=\frac{k_1\Lambda _h}{k_3\lambda ^{*}_h+k_1\mu },\,\,\, I^{*}_h=\frac{\lambda ^{*}_h}{k_1}S^{*}_h,\,\,\, S^{*}_v=\frac{\Lambda _v}{\lambda ^{*}_v+\eta },\,\,\, E^{*}_v=\frac{\lambda ^{*}_v}{k_2}S^{*}_v,\,\,\, I^{*}_v=\frac{\gamma \lambda ^{*}_v}{k_2\eta \varphi _I}S^{*}_v, \end{aligned}$$
(7)

where we have used the notation,

$$\begin{aligned} k_1=\mu +\alpha +\delta ,\;\;\;k_2=\varphi _E \eta + \gamma ,\;\;\; \text { and } \;\;\; k_3=\mu +\alpha . \end{aligned}$$
(8)

Substituting (7) in (6) we get

$$\begin{aligned} \lambda ^{*}_h=\varphi _I\omega \pi _h\frac{\gamma \lambda ^{*}_v(k_1\mu +k_3\lambda ^{*}_h)}{k_2\eta \varphi _I\Lambda _h(k_1+p\lambda ^{*}_{h})}\frac{\Lambda _v}{(\eta +\lambda ^{*}_v)}, \end{aligned}$$
(9)

and

$$\begin{aligned} \lambda ^{*}_v=\omega \pi _m p\frac{\lambda ^{*}_h}{k_1+p \lambda ^{*}_h}. \end{aligned}$$
(10)

By substituting (10) in (9), it can be shown that equilibria components satisfy the following equation,

$$\begin{aligned} \lambda ^{*}_h\left[ a_0(\lambda ^{*}_h)^{2}+b_0\lambda ^{*}_h+c_0\right] =0, \end{aligned}$$
(11)

where the coefficients are given by,

$$\begin{aligned} a_0&= \left( \,\pi _{m}\,\omega +\eta \right) k_{2}\,\eta \,\Lambda _{h}p^2, \end{aligned}$$
(12a)
$$\begin{aligned} b_0&= \left( \pi _{m}\omega +2\eta \right) k_{1}k_{2}\eta \Lambda _{h}p-k_{3}\pi _{h}\pi _{m} \omega ^2 p\Lambda _{v}\gamma , \end{aligned}$$
(12b)
$$\begin{aligned} c_0&= k_{1}^2k_{2}\eta ^2\Lambda _{h}\left( 1-R^{2}_0\right) , \end{aligned}$$
(12c)

where \(R_0\) is the basic reproduction number, given by (4). Equation (11) admits a trivial solution \(\lambda ^{*}_h=0\) which corresponds to the disease-free equilibrium \(E_0\) (3). Now, we assume \(\lambda ^{*}_h\ne 0\). The existence of endemic equilibria is regulated by the quadratic equation \(a_0(\lambda ^{*}_h)^{2}+b_0\lambda ^{*}_h+c_0=0\). Note that the coefficient \(a_0\) is always positive, and \(c_0\) is positive (resp. negative) if \(R_0\) is less than (resp. greater than) unity, respectively. The coefficient \(b_0\) may be rearranged as:

$$\begin{aligned} b_0=\frac{k_{1}k_{2}k_{3}\eta ^{2}\Lambda _{h}}{\mu }\left( R^{2}_c-R^{2}_0\right) , \end{aligned}$$

where

$$\begin{aligned} R_c=\sqrt{\frac{\mu p(\pi _{m}\omega +2\eta )}{k_{3}\eta }}. \end{aligned}$$
(13)

It follows that the number of endemic equilibria of model (1) depends on the coefficients \(a_0\), \(b_0\) and \(c_0\) as follows:

  1. (1)

    There is a unique endemic equilibrium if \(c_0<0\)  (i.e., \(R_0>1\));

  2. (2)

    There is a unique endemic equilibrium if

    $$\begin{aligned} (b_0<0\;\;\; \mathrm{and}\;\;\; c_0=0)\;\;\; \mathrm{or} \;\;\; (b_0<0,\;\;\; c_0>0\;\;\;\mathrm{and}\;\;\; b^{2}_0-4a_0c_0=0) ; \end{aligned}$$
    (14)
  3. (3)

    There are two endemic equilibria if

    $$\begin{aligned} b_0<0,\;\;\; c_0>0\;\;\;\mathrm{and}\;\;\; b^{2}_0-4a_0c_0>0; \end{aligned}$$
    (15)
  4. (4)

    There are no endemic equilibria otherwise.

The results of this section may be summarized in the following:

Theorem 2

If \(R_0<1\), there exists an endemic equilibrium if conditions (14) are satisfied; two endemic equilibria if conditions (15) are satisfied; and no endemic equilibria otherwise. If \(R_0>1\), then there exists a unique endemic equilibrium.

A relevant aspect of this result is that conditions (15) indicate the occurrence of multiple endemic equilibria for \(R_0<1\). Specifically, the disease-free equilibrium may co-exist with one or two endemic equilibria. From an epidemiological perspective, this means that the elimination of the disease in the population is no longer guaranteed by the classical threshold condition \(R_0<1\). A new, smaller, threshold for \(R_0\) must be determined. To this aim, we now express condition (15) in terms of the basic reproduction number \(R_0\) as follows. Note that coefficient \(b_0<0\) is equivalent to \(R_0>R_c\), and \(c_0>0\) is equivalent to \(R_0<1\). Note also that \(b_0^2-4a_0c_0>0\) is equivalent to

$$\begin{aligned} a_1R^{4}_0+b_1R^{2}_0+c_1>0, \end{aligned}$$
(16)

where,

$$\begin{aligned} a_1&= \frac{k_{1}^2\,k_{2}^2\,k_{3}^2\,\eta ^4\,\Lambda _{h}^2}{\mu ^2}>0, \\ b_1&= \frac{2\,k_{1}^2\,k_{2}^2\,\eta ^3\,\Lambda _{h}^2\,p\,\left( 2(\pi _{m}\mu \omega p+\eta \mu p-k_{3}\eta )-k_{3}\,\pi _{m}\,\omega \right) }{\mu }, \\ c_1&= k_{1}^2\,k_{2}^2\,\eta ^2\,\Lambda _{h}^2\,\pi _{m}^2\,\omega ^2\,p^2>0. \end{aligned}$$

Equation (16) admits positive real roots if and only if \(b_1<0\) and \(\Delta =b_1^2-4a_1c_1\ge 0\). We can write

$$\begin{aligned} \Delta =\frac{16k_{1}^4k_{2}^4\eta ^6\Lambda _{h}^4\left( \pi _{m} \omega +\eta \right) p^2\left( \mu p-k_{3}\right) \psi }{\mu ^2}, \end{aligned}$$

where

$$\begin{aligned} \psi =\left( \pi _{m}\mu \omega p+\eta \mu p-k_{3}\eta \right) . \end{aligned}$$
(17)

Choosing \(\psi <0\) ensures that \(\mu p-k_{3}<0\), which implies \(\Delta >0\) and \(b_1<0\).

Setting

$$\begin{aligned} \begin{array}{ll} R_{\pm }&=\sqrt{\frac{-b_1\pm \sqrt{\Delta }}{2a_1}}=\sqrt{\frac{\mu p}{\eta k_{3}^2}} \left| \sqrt{-\psi }\pm \sqrt{-(\mu p-k_{3})(\pi _{m}\omega +\eta )}\right| , \end{array} \end{aligned}$$
(18)

it follows that condition (15) is equivalent to

$$\begin{aligned} R_c<R_0<\min (1,R_{-})\quad \mathrm {or}\quad \max (R_c,R_+)<R_0<1. \end{aligned}$$
(19)

Remark 1

Condition (19) can be also expressed in terms of \(\omega \). Setting,

$$\begin{aligned} \bar{\omega }={{k_{1}\,k_{2}\,\eta \,\Lambda _{h}\,\pi _{m}+ \eta \,\sqrt{k_{1}\,k_{2}\,\Lambda _{h}\,\pi _{m}\, \left( 8\,k_{3}\,\pi _{h}\,\Lambda _{v}\,\gamma +k_{1}\,k_{2}\,\Lambda _{ h}\,\pi _{m}\right) }}\over {2\,k_{3}\,\pi _{h}\,\pi _{m}\Lambda _{ v}\,\gamma }}, \end{aligned}$$
(20)

and using the expression of \(R_0\), we obtain,

$$\begin{aligned} \bar{\omega }<\omega <\min (\omega ^{*},\omega _{-})\quad \mathrm{{or}}\quad \hbox {max}(\bar{\omega }, \omega _{+})<\omega <\omega ^{*}, \end{aligned}$$
(21)

where,

$$\begin{aligned} \omega _{\pm }=\frac{1}{k_{3}}\sqrt{ \dfrac{k_1k_2\eta \Lambda _h}{\pi _h\pi _m\gamma \Lambda _v}} \left| \sqrt{-\psi }\pm \sqrt{-(\mu p-k_{3})(\pi _{m}\omega +\eta )}\right| . \end{aligned}$$
(22)

5 Bifurcation analysis

In this section we show that the sub-threshold occurrence of multiple endemic equilibria, as stated in Theorem 2, is the result of a transcritical backward (subcritical) bifurcation at \(R_0=1\). This will also provide insight on the local stability properties of the endemic equilibria emerging from the bifurcation.

We study the centre manifold near the criticality by using the approach developed in [7, 14, 15], based on general centre manifold theory [18]. In summary, this approach establishes that the normal form representing the dynamics of the system on the centre manifold is given by \(\dot{u} = a u^2+ b \xi u\), where,

$$\begin{aligned} a=\frac{{\mathbf v}}{2} \cdot D_{{\mathbf x}{\mathbf x}}{\mathbf f}({\mathbf x}_0,0){\mathbf w}^2 \equiv \frac{1}{2} \displaystyle \sum _{k,i,j=1}^{n} v_{k} w_{i} w_{j} \displaystyle \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial x_{j}} ({\mathbf x}_0,0), \end{aligned}$$
(23)

and

$$\begin{aligned} b= {\mathbf v} \cdot D_{{\mathbf x}\xi }{\mathbf f}({\mathbf x}_0,0){\mathbf w} \equiv \displaystyle \sum _{k,i=1}^{n} v_{k} w_{i} \displaystyle \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial \xi } ({\mathbf x}_0,0). \end{aligned}$$
(24)

Here, the symbol \(\xi \) denotes a bifurcation parameter to be chosen, \(f_i\)s denote the right hand side of system (1), \({\mathbf x}\) denotes the state vector, \({\mathbf x}_0\) the disease-free equilibrium \(E_0\), \(D_{\mathbf {x}}\) denotes the differential operator with respect to \(\mathbf {x}\), \(D_{\xi }\) denotes the differential operator with respect to \(\xi \), and v and w denote the left and right eigenvectors, respectively, corresponding to the null eigenvalue of the Jacobian matrix of system (1) evaluated at \({\mathbf x}_0\) for \(\xi =0\).

We choose the mosquito biting rate, \(\omega \), as the bifurcation parameter. We observe that \(R_0=1\) is equivalent to:

$$\begin{aligned} \omega =\omega ^{*}:=\sqrt{\frac{k_1k_2\eta ^{2}\Lambda _h}{p\pi _h\pi _m\mu \Lambda _v\gamma }}, \end{aligned}$$
(25)

so that the disease-free equilibrium \(E_0\) is locally asymptotically stable when \(\omega <\omega ^{*}\), and unstable when \(\omega >\omega ^{*}\) . Hence, \(\omega =\omega ^{*}\) is a bifurcation value.

The Jacobian matrix of system (1), evaluated at \(E_0\) for \(\omega =\omega ^{*}\) is given by

$$\begin{aligned} \mathcal {J}(E_0, \omega ^{*})=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -\mu &{}\delta &{}0&{}0&{}-\varphi _I\omega ^{*}\pi _h\\ 0&{}-k_1&{}0&{}0&{}\varphi _I\omega ^{*}\pi _h\\ 0&{}-\omega ^{*}\pi _m p\frac{S^{0}_v}{S^{0}_h}&{}-\eta &{}0&{}0\\ 0&{}\omega ^{*}\pi _m p\frac{S^{0}_v}{S^{0}_h}&{}0&{}-k_2&{}0\\ 0&{}0&{}0&{}\gamma &{}-\varphi _I\eta \end{array}\right) , \end{aligned}$$

where \(k_1\) and \(k_2\) are defined in (8). The eigenvalues are given by \(\lambda _1=-\mu \), \(\lambda _2=-\eta \), and \(\lambda _3\), \(\lambda _4\), \(\lambda _5\) eigenvalues of the submatrix,

$$\begin{aligned} \bar{\mathcal {J}}= \left( \begin{array}{c@{\quad }c@{\quad }c} -k_1&{}0&{}\varphi _I\omega ^{*}\pi _h\\ \omega \pi _m p\frac{S^{0}_v}{S^{0}_h}&{}-k_2&{}0\\ 0&{}\gamma &{}-\varphi _I\eta \end{array}\right) . \end{aligned}$$

The characteristic equation of \(\bar{\mathcal {J}}\) is given by

$$\begin{aligned} x^3+A_1x^2+A_2x+A_3=0, \end{aligned}$$
(26)

where

$$\begin{aligned} A_1=\eta \varphi _{I}+k_{2}+k_{1},\;\;\;\; A_2=\left( k_{2}+k_{1}\right) \eta \varphi _{I}+k_{1}k_{2},\;\;\;\; A_3=k_{1}k_{2}\eta \varphi _{I}\left( 1-R^2_0\right) , \end{aligned}$$

and \(R_0\) is given by (4). Since \(R_0=1\) at the criticality, equation (26) becomes

$$\begin{aligned} x\left( x^2+A_1x+A_2\right) =0. \end{aligned}$$
(27)

Thus, the Jacobian \(J^{*}\) of the linearised system has a simple zero eigenvalue and the other eigenvalues have negative real part. Therefore the disease-free equilibrium \(E_0\) is a nonhyperbolic equilibrium. In order to determine the coefficients (23) and (24), we look for the right and left eigenvectors corresponding to the zero eigenvalue. The components \(w_i\), for \(i=1,\cdots ,5\), of the right eigenvector \(\mathbf {w}\) are given by:

$$\begin{aligned}&\displaystyle -\mu w_1+\delta w_2-\varphi _I\omega ^{*}\pi _hw_5 = 0, \\&\displaystyle -k_1w_2+\varphi _I\omega ^{*}\pi _hw_5 =0, \\&\displaystyle -\omega ^{*}p \pi _m\frac{S^{0}_v}{S^{0}_h}w_2-\eta w_3 =0, \\&\displaystyle \omega ^{*}p \pi _m\frac{S^{0}_v}{S^{0}_h}w_2-k_2w_4 =0, \\&\displaystyle \gamma w_4-\varphi _I\eta w_5 =0. \end{aligned}$$

Analogously, the components \(v_i\), for \(i=1,\cdots ,5\), of the left eigenvector \(\mathbf {v}\) are given by,

$$\begin{aligned} -\mu v_1= & {} 0, \\ \delta v_1-k_1v_2-\omega ^{*}p \pi _m\frac{S^{0}_v}{S^{0}_h}(v_3-v_4)= & {} 0, \\ -\eta v_3= & {} 0, \\ -k_2v_4+\gamma v_5= & {} 0, \\ -\varphi _I\omega ^{*}\pi _h(v_1-v_2)-\varphi _I\eta v_5= & {} 0. \end{aligned}$$

Therefore for \(w_5>0,\;\;v_5>0\), we have,

$$\begin{aligned} w_1&= -\frac{\varphi _I\omega ^{*}\pi _hk_3}{k_1\mu }w_5, \\ w_2&= \frac{\varphi _I\omega ^{*}\pi _h}{k_1}w_5, \\ w_3&= -\frac{(\omega ^{*})^{2}p\pi _h\pi _m\varphi _IS^{0}_v}{S^{0}_h\eta k_1}w_5,\\ w_4&= \frac{\varphi _I\eta }{\gamma }w_5, \end{aligned}$$

and,

$$\begin{aligned} v_1 = 0, \;\;\; v_2 =\frac{\eta }{\omega ^{*}\pi _h}v_5, \;\;\; v_3 = 0, \;\;\; v_4 = \frac{\gamma }{k_2}v_5. \end{aligned}$$

Considering only the nonzero components of the left eigenvector, \(\mathbf {v}\), it follows that:

$$\begin{aligned} a&= \frac{1}{2}\left( 2v_2w_2w_5\frac{\partial ^{2} f_2}{\partial I_h\partial I_v}({\mathbf x}_0,0) +2v_4w_{1}w_2\frac{\partial ^{2}f_{4}}{\partial S_{h} \partial I_{h}} ({\mathbf x}_0,0) +v_4w_2w_{2}\frac{\partial ^{2}f_{4}}{\partial I^{2}_{h}} ({\mathbf x}_0,0) \right. \\&\quad {} + \left. 2v_4w_{2}w_{3}\frac{\partial ^{2}f_{4}}{\partial I_{h} \partial S_{v}} ({\mathbf x}_0,0)\right) , \end{aligned}$$

where,

$$\begin{aligned} \frac{\partial ^{2} f_2}{\partial I_h\partial I_v}({\mathbf x}_0,0)&= -\varphi _I\omega ^{*}p \pi _h\frac{1}{S^{0}_h}, \\ \frac{\partial ^{2}f_{4}}{\partial S_{h} \partial I_{h}} ({\mathbf x}_0,0)&= -\omega ^{*}p \pi _m\frac{S^{0}_v}{\left( S^{0}_h\right) ^{2}}, \\ \frac{\partial ^{2}f_{4}}{\partial I^{2}_{h}} ({\mathbf x}_0,0)&= -2\omega ^{*}p^{2}\pi _m\frac{S^{0}_v}{\left( S^{0}_h\right) ^{2}}, \\ \frac{\partial ^{2}f_{4}}{\partial I_{h} \partial S_{v}} ({\mathbf x}_0,0)&= \omega ^{*}p\pi _m\frac{1}{S^{0}_h}, \end{aligned}$$

so that,

$$\begin{aligned} a =-\frac{\pi _{h}\mu \omega ^{*}p\varphi _{I}^2 }{k_{1}^2k_{2}\eta ^2\Lambda _{h}^2}v_{5}w_{5}^2A_0, \end{aligned}$$

where,

$$\begin{aligned} A_0= & {} \left( \pi _{h}\pi _{m}^2\mu (\omega ^{*})^3p\Lambda _{v}\gamma + \eta \pi _{h}\pi _{m}\mu (\omega ^{*})^2 p\Lambda _{v}\gamma \right. \\&\left. -\,k_{3}\eta \pi _{h}\pi _{m}(\omega ^{*})^2\Lambda _{v}\gamma +k_{1}k_{2}\eta ^3\Lambda _{h}\right) . \end{aligned}$$

The analysis performed in this sections may be summarized in the following theorem:

Theorem 3

If \(A_0<0\), then the malaria model (1) exhibits a backward bifurcation at \(R_0=1\). If \(A_0 > 0\), then the bifurcation is forward.

Remark 2

The change of stability of \(E_0\), from being stable to unstable, as \(R_0\) crosses the critical value \(R_0=1\), implies that \(b>0\) (see [14]). In our case, direct calculations shows that

$$\begin{aligned} b=\varphi _I\pi _hv_2w_5 +p\pi _m ({S^{0}_v}/{S^{0}_h}) v_4w_2>0. \end{aligned}$$

In the special case where there is no disease-induced death, i.e, \(\alpha =0\), we have

$$\begin{aligned} \begin{array}{ll} A_0&=\dfrac{1}{p}\left( \eta ^3 \pi _{h}\pi _{m}^2\mu p^2 \Lambda _{v}\gamma \Theta ^{\frac{3}{2}} +\eta ^3\Lambda _{h}\left( \mu +\delta \right) \left( 2p-1\right) \left( \gamma +\eta \varphi _{E}\right) \right) , \end{array} \end{aligned}$$

where

$$\begin{aligned} \Theta =\left( \dfrac{\Lambda _{h}\left( \mu +\delta \right) \gamma +\eta \Lambda _{h}\left( \mu +\delta \right) \varphi _{E}}{\pi _{h}\pi _{m}\mu p\Lambda _{v}\gamma }\right) . \end{aligned}$$

Since, by definition, \(p>1 \implies 2p-1>0\), it follows that in absence of disease induced death, the bifurcation is forward. Indeed, \(\alpha =0 \implies A_0>0 \implies a<0\).

Finally, note also that when \(\alpha =0\), the coefficients of equation (11) become,

$$\begin{aligned} a_0&= \left( \pi _{m}\omega +\eta \right) p^3>0, \\ b_0&= \left( \mu +\delta \right) \left( \pi _{m}\omega p+\eta (2p-R_{0}^2)\right) p>0, \\ c_0&= \eta p\left( \mu +\delta \right) ^2(1-R_{0}^2). \end{aligned}$$

We see that \(a_0\) is always positive. Additionally, since \(p>1\), it follows that \(b_0\) and \(c_0\) are always nonnegative whenever \(R_0<1\). Therefore, there are no endemic equilibria bifurcating from the disease-free equilibrium when \(R_0<1\).

6 Numerical simulations

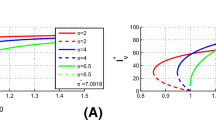
We illustrate the backward bifurcation with numerical simulations in Figure 1 using the set of parameter values listed in Table 1, except with \(\Lambda _h=4\), \(\mu =1/(30\cdot 365)\), \(\Lambda _v=10^8/14\), \(\alpha =10^{-3}\), \(\delta =1/100\), \(\eta =1/14\), \(\pi _h=0.75\), \(\pi _m=0.8\), \(\varphi _E=1\), \(\varphi _I=2\), \(p=4\), and varying \(\omega \). In the particular case \(\omega =4.802\times 10^{-4}\), the conditions required by Theorem 2, case (15), are satisfied, as well as \(A_0=-0.0000020 <0\) (so that \( a=0.00000020>0\)) in Theorem 3. In particular, for this set of parameter values, \(R_{c}=0.8193476<1\), \(R_{0}=0.9452627<1\), \(\psi =-5.1714\times 10^{-5}\), \(R_{+}=0.9444190\), \(R_{-}=0.0020\) (so that \(\max (R_{c},R_{+})<R_{0}<1\)). Furthermore, \(a_0=0.0533>0\), \(b_0=- 0.0000977<0\) and \(c_0=4.342\times 10^{-8}>0\), so that \(b_{0}^{2}-4a_0c_0=2.750\times 10^{-10}>0\). The resulting two endemic equilibria \(E=(S^{*}_h,I^{*}_h,S^{*}_v,E^{*}_v,I^{*}_v)\), are given by: \(E^{*}=(20333, 1964, 99850354, 65808, 41919 )\), which is locally asymptotically stable and \(E^{**}=(24079, 1650, 99884413, 50830, 32379 )\), which is unstable.

Fig. 1
figure 1

Bifurcation diagrams for model (1) in the \((R_0, I^{*}_{v})\) and \((R_0, I^{*}_{h})\) planes. The parameter \(\omega \) is varied in the range (0, 0.000534] to allow \(R_{0}\) to vary in the range (0, 1.05]. Two endemic equilibrium points coexist for values of \(\omega \) in the range (\(4.798\times 10^{-4}\), \(5.080\times 10^{-4}\)) (corresponding to the range (0.9444, 1) of \(R_{0}\)). Solid lines represent stable equilibria and dashed lines represent unstable equilibria.

Full size image
Fig. 2
figure 2

One dimensional sensitivity analysis of \(R_0\) to p with all other parameter values as specified in Table 1 except for \(\varphi _I=2\) and \(\varphi _E=1\)

Full size image

Figure 2 shows that increasing the relative attractiveness of infectious humans, p, increases \(R_0\). Figure 3 shows numerical simulations of the malaria model (1) for different values of p. The curve for \(p=1\) shows the result for the assumption used in most malaria models: that malaria infection makes no difference to the attractiveness of humans. We see here that increasing p decreases the equilibrium prevalence of infectious humans, contrary to the effect of p on \(R_0\), but does not affect the equilibrium prevalence of infectious mosquitoes.

Fig. 3
figure 3

Numerical simulations of the malaria model (1) for parameter values as specified in Table 1 except for \(\varphi _I=2\), \(\varphi _E=1\), and p varied as shown in the legend

Full size image
Fig. 4
figure 4

One dimensional sensitivity analysis of \(R_0\) to \(\varphi _E\) with all other parameter values as specified in Table 1 except for \(\varphi _I=2\)

Full size image

Figure 4 shows that increasing the relative biting frequency of exposed mosquitoes, \(\varphi _E\), decreases \(R_0\). Figure 5 shows numerical simulations of (1) for different values of \(\varphi _E\). Consistent with the effect on \(R_0\), increasing \(\varphi _E\) decreases the equilibrium prevalence of infectious humans and mosquitoes (with a stronger impact on the prevalence of mosquitoes).

Fig. 5
figure 5

Numerical simulations of the malaria model (1) for parameter values as specified in Table 1 except for \(\varphi _I=1\) and \(\varphi _E\) varied as shown in the legend

Full size image
Fig. 6
figure 6

Numerical simulations of the malaria model (1) for parameter values as specified in Table 1 except for \(\varphi _E=1\) and \(\varphi _I\) varied as shown in the legend

Full size image

The relative biting frequency of infectious mosquitoes does not appear in the expression for \(R_0\) so changing this parameter has no effect on \(R_0\). Figure 6 shows numerical simulations of (1) for different values of \(\varphi _I\). Increasing \(\varphi _I\) makes no difference to the equilibrium prevalence of infectious humans, but leads to a large decrease in the equilibrium prevalence of infectious mosquitoes.

Fig. 7
figure 7

Two dimensional sensitivity analysis of \(R_0\) to p and \(\varphi _E\) with all other parameter values as specified in Table 1 except for \(\varphi _I=2\)

Full size image

Figure 7 shows that the effects of simultaneously increasing p and \(\varphi _E\) on \(R_0\) are consistent with the one-dimensional sensitivity analyses shown in Figures 2 and 4. Additionally, as p increases, the dependence of \(R_0\) on \(\varphi _E\) increases.

7 Discussion and conclusions

We developed and analysed a simple malaria model to investigate the impact of relaxing three assumptions that mathematical models of malaria commonly make. We allowed the relative attractiveness of infectious humans (as compared to susceptible humans) to mosquitoes to increase; the feeding frequency of exposed mosquitoes (as compared to susceptible mosquitoes) to decrease; and the feeding frequency of infectious mosquitoes (as compared to susceptible mosquitoes) to increase.

We derived the basic reproductive number, \(R_0\), that provides a threshold condition for when the disease-free equilibrium loses stability. We showed that in common with many similar models of malaria, there is a transcritical bifurcation at \(R_0=1\), that can be forward or backward depending on the parameter values, and is always forward if there is no disease-induced death rate. We provided threshold conditions for the direction of the bifurcation and the existence of zero, one or two endemic equilibrium points.

As may be expected, we showed that as the relative attractiveness of infectious humans, p, increases, \(R_0\) increases. However, we also showed the surprising result that as p increases, the equilibrium proportion of infectious humans decreases, even as \(R_0\) increases. This is because mosquitoes repeatedly bite infectious humans so they are less likely to pass the infection to susceptible humans, and therefore the same proportion of infectious mosquitoes leads to a lower proportion of infectious humans for higher values of p.

We showed that as the relative biting rate of exposed mosquitoes, \(\varphi _E\), increases, \(R_0\) and the equilibrium proportion of infectious humans and mosquitoes decreases. This is reasonable because as the biting rate of exposed mosquitoes increases, their mortality increases so fewer exposed mosquitoes are likely to survive to become infectious.

We finally showed that varying the relative biting rate of infectious mosquitoes, \(\varphi _I\), has no impact on \(R_0\) because the increased biting rate is cancelled by the shorter life span of the infectious mosquitoes. Correspondingly, varying \(\varphi _I\) has no impact on the equilibrium proportion of infectious humans. However, increasing \(\varphi _I\) leads to a substantial decrease in the equilibrium proportion of infectious mosquitoes because of their higher death rate. Importantly for malaria transmission, these fewer infectious mosquitoes are able to maintain transmission to humans at a higher level than if their biting rate was lower. These analyses of a simple malaria model show that common assumptions around the relative attractiveness of infectious humans and the relative biting rates of exposed and infectious mosquitoes can have substantial and counter-intuitive effects on malaria transmission dynamics.