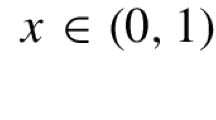Abstract
In this paper we study the stability of the solutions of some nonlinear Neumann problems, under perturbations of the domains in the Hausdorff complementary topology. We consider the problem
where \({{\mathbf{R}^n \times \mathbf{R}^n \rightarrow \mathbf{R}^n}}\) is a Caratheodory function satisfying the standard monotonicity and growth conditions of order p, 1 < p < ∞. If Ω h is a uniformly bounded sequence of connected open sets in R n, n ≥ 2, we prove that if \({{\Omega_{h}^{c} \rightarrow \Omega^{c}}}\) in the Hausdorff metric, \({|\Omega_{h}| \rightarrow |\Omega|}\) and the geodetic distances satisfy the inequality \({d_{\Omega}\left( x,y\right) \leq \liminf_{h} d_{\Omega_{h}} \left( x,y\right)}\) for every \({x, y \in \Omega,}\) then \({\nabla u_{\Omega_h} \rightarrow\nabla u_{\Omega}}\) strongly in L p, provided that W 1, ∞(Ω) is dense in the space L 1, p(Ω) of all functions whose gradient belongs to L p(Ω, R n).
Similar content being viewed by others
References
Bucur D., Varchon N.: A duality approach for the boundary variation of Neumann problems. SIAM J. Math. Anal. 34, 460–477 (2002)
Dal Maso G., Ebobisse F., Ponsiglione M.: A stability result for nonlinear Neumann problems under boundary variations. J. Math. Pures Appl. 82, 503–532 (2003)
Chambolle A., Doveri F.: Continuity of Neumann linear elliptic problems on varying two-dimensional bounded open sets. Comm. Partial Differ. Equ. 22, 811–840 (1997)
Dal Maso G., Toader R.: A model for the quasi-static growth of brittle fractures: existence and approximation results, Arch. Ration. Mech. Anal. 162, 101–135 (2002)
Ebobisse F., Ponsiglione M.: A duality approach for variational problems in domains with cracks. J. Convex Anal. 11(1), 17–40 (2004)
Maz’ya V.G.: Sobolev Spaces. Springer, Berlin (1985)
Mosco U.: Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 3, 510–585 (1969)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Carbone.
Rights and permissions
About this article
Cite this article
Acanfora, F. A contribution to stability theory for nonlinear Neumann problem. Ricerche mat. 61, 299–306 (2012). https://doi.org/10.1007/s11587-012-0131-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11587-012-0131-7
Keywords
- Nonlinear Neumann problems
- Monotone operators
- Perturbations of domains
- Hausdorff complementary topology