Combined effects of LTP/LTD and synaptic scaling in formation of discrete and line attractors with persistent activity from non-trivial baseline

Abstract

In this article, we analyze combined effects of LTP/LTD and synaptic scaling and study the creation of persistent activity from a periodic or chaotic baseline attractor. The bifurcations leading to the creation of new attractors have been detailed; this was achieved using a mean field approximation. Attractors encoding persistent activity can notably appear via generalized period-doubling bifurcations, tangent bifurcations of the second iterates or boundary crises, after which the basins of attraction become irregular. Synaptic scaling is shown to maintain the coexistence of a state of persistent activity and the baseline. According to the rate of change of the external inputs, different types of attractors can be formed: line attractors for rapidly changing external inputs and discrete attractors for constant external inputs.

Appendices

Appendix 1: Parameters typically used for simulations

See Appendix Table 1

Table 1 Parameters typically used in the simulations

Appendix 2: Approximation of the effects of LTP/LTD alone

In the following, changes due to LTP/LTD are considered. From Eqs. (1)–(3), by taking the time average over $\{ n-T_0, \ldots, n-1 \}$, we obtain the following expression:

$$ \begin{aligned} Y_i(n) &= {\frac{y_i(n-T_0) - y_i(n)}{T_0}} \\ &+ k Y_i(n) + {\frac{1}{T_0}} \sum_{l=1}^{T_0} \sum_{i \neq j} \omega_{ij}(n-l) x_j(n-l) - \alpha X_i(n) + \theta_i + A_i,\\ &= k Y_i(n) + {\frac{1}{T_0}} \sum_{l=1}^{T_0} \sum_{i \neq j} \omega_{ij}(n-l) x_j(n-l) - \alpha X_i(n) + \theta_i + A_i\\ &+ {{\mathcal{O}}}({\frac{1}{T_0}}), \end{aligned} $$

(45)

where A _i  = a _i f _i is the “perceived” external input (see section "External inputs"), i.e., the level of external input averaged over window T ₀.

The changes in connectivity in the window T ₀ can be considered to be very small (quasi-constant). Note that for l < T ₀ and e = 1 (see Eq. (7)),

$$ \begin{aligned} \omega_{ij} (n-l) &= \omega_{ij} (n) -\sum_{t=1}^{l} \Uplambda_{ij} (n-t), \\ &= \omega_{ij} (n) +{{\mathcal{O}}}(T_0 \lambda). \end{aligned} $$

(46)

By using Eq. (46) in Eq. (45), noting that ${{\frac{1}{T_0}} \sum\nolimits_{i \neq j} \sum\nolimits_{l=1}^{T_0} \sum\nolimits_{t=1}^{l} \Uplambda_{ij} (n-t) = {\mathcal{O}}(T_0 \lambda M),}$ we rewrite Eq. (45) as follows (T ₁ ≫ T ₀, thus ${\frac{1}{T_0}} \gg T_0 \lambda M$):

$$ Y_i(n) = k Y_i(n) + \sum_{i \neq j} \omega_{ij}(n) X_j(n) - \alpha X_i(n) + \theta_i + A_i + {{\mathcal{O}}}\left({\frac{1}{T_0}}\right). $$

(47)

By considering the changes in weights and activity over window T ₁, we rewrite Eq. (47) as follows:

$$ \begin{aligned} Y_i(n) &= k Y_i(n) \\ &+ \sum_{i \neq j} (\omega_{ij}(n-T_1) + \Updelta^{T_1} \omega_{ij}(n))(X_j(n-T_1) + \Updelta^{T_1} X_j(n)) \\ &- \alpha (X_i(n-T_1) + \Updelta^{T_1} X_i(n)) + \theta_i + A_i + {{\mathcal{O}}}\left({\frac{1}{T_0}}\right). \end{aligned} $$

(48)

The above equation can also be written as follows:

$$ Y_i(n) = Y_i(n-T_1) + {\frac{1}{1-k}}(t_1 + t_2 + t_3 + t_4) + {{\mathcal{O}}}\left({\frac{1}{T_0}}\right), $$

(49)

where:

$$ t_1 = \sum_{i \neq j} \omega_{ij}(n-T_1) \Updelta^{T_1} X_j(n), $$

(50)

$$ t_2 = \sum_{i \neq j} \Updelta^{T_1} \omega_{ij}(n) X_j(n-T_1), $$

(51)

$$ t_3 = \sum_{i \neq j} \Updelta^{T_1} \omega_{ij}(n) \Updelta^{T_1} X_j(n), $$

(52)

$$ t_4 = - \alpha \Updelta^{T_1} X_i(n). $$

(53)

When the changes in weights are considered over a limited number of steps n such that $n \lambda \ll \bar{\omega}$ and the assumption of Eq. (19) is verified, the following approximations hold, ∀ n:

$$ \omega_{ij}(n) = {{\mathcal{O}}}\left({\frac{\bar{\omega}}{M}}\right), $$

(54)

$$ \Updelta^{T_1} \omega_{ij}(n) = {{\mathcal{O}}}(T_1 \lambda), $$

(55)

$$ \Updelta^{T_1} X_j(n) = {{\mathcal{O}}}(p \epsilon). $$

(56)

Then the terms of Eqs. (50)–(53) are approximated as follows:

$$ t_1 = {{\mathcal{O}}}(\bar{\omega} p \epsilon), $$

(57)

$$ t_2 = {{\mathcal{O}}}(\epsilon), $$

(58)

$$ t_3 = {{\mathcal{O}}}(p \epsilon^2), $$

(59)

$$ t_4 = {{\mathcal{O}}}\left({\frac{\bar{\omega} p \epsilon}{M}}\right). $$

(60)

Finally, because $\bar{\omega} p \ll 1$ and $\bar{\omega} p \epsilon \gg {\frac{1}{T_0}},$ the approximation of Eq. (21) holds.

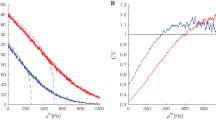
To verify the validity of the approximation, the terms t ₁, t ₂, t ₃ and t ₄ are compared for several steps $m T_1, m = \{1, 2, \ldots\},$ as shown in Fig. 18. Simulations confirm that as long as the change in weights remains small, t ₂ is dominant. Note that because ${t_2 = {\mathcal{O}}(\epsilon),}$ this approximation is consistent with the assumption of Eq. (20) as applied to the change in Y _i (n).

Fig. 18

Comparison of terms t ₁, t ₂, t ₃ and t ₄ of Eqs. (50)–(53), respectively, with the solid, dashed, dotted, and dash-dot lines in terms of steps $m T_1, m = \{1, 2, \ldots\}$. So long as the change in weights remains small (i.e., for a small number of time steps m in this figure), the term t ₂ is dominant

Appendix 3: Approximation of the combined effects of LTP/LTD and synaptic scaling

When the weights are scaled by synaptic scaling (see Eqs. (12) and (13)), the change in synaptic efficacy $\Updelta^{T_1} \omega_{ij} (n) = \omega_{ij} (n) - \omega_{ij} (n-T_1)$ is given as follows:

$$ \begin{aligned} \Updelta^{T_1} \omega_{ij} (n) &= (1-r) \omega_{ij} (n_0) + r\Uplambda_{ij} (n-1) + r \omega_{ij} (n-1),\\ &=(1-r^{T_1}) \omega_{ij} (n_0) + \sum_{t=1}^{T_1} r^t \Uplambda_{ij} (n-t) + (r^{T_1}-1) \omega_{ij} (n-T_1). \end{aligned} $$

(61)

The change in weights $\Updelta^{T_1} \omega_{ij}$ when synaptic scaling is active is of the same magnitude as that when only LTP/LTD modify the weights (see Eq. (14)). Therefore, the approximation of Eq. (21) still holds in this case. Then, the time-averaged internal state can be written as follows using Eqs. (21) and (61) as follows:

$$ \begin{aligned} Y_i(n) &= Y_i(n-T_1) \\ &+ {\frac{1-r^{T_1}}{1-k}} \sum_{i \neq j} \omega_{ij} (n_0) X_j(n-T_1)\\ &+ {\frac{1}{1-k}} \sum_{i \neq j} \left[\sum_{t=1}^{T_1} r^t \Uplambda_{ij} (n-t) \right] X_j(n-T_1) \\ &+ {\frac{r^{T_1}-1}{1-k}} \sum_{i \neq j} \omega_{ij} (n-T_1) X_j(n-T_1) \\ &+ {{\mathcal{O}}}(\eta). \end{aligned} $$

(62)

By using Eq. (47), we rewrite this equation as follows:

$$ \begin{aligned} Y_i(n) &= Y_i(n-T_1) \\ &+ {\frac{1-r^{T_1}}{1-k}} \sum_{i \neq j} \omega_{ij} (n_0) X_j(n-T_1)\\ &+ {\frac{1}{1-k}} \sum_{i \neq j} \left[\sum_{t=1}^{T_1} r^t \Uplambda_{ij} (n-t)\right] X_j(n-T_1) \\ &+ {\frac{r^{T_1}-1}{1-k}} ((1-k) Y_i(n-T_1) + \alpha X_i(n - T_1) - \theta_i - A_i)\\ &+ {{\mathcal{O}}}(\eta). \end{aligned} $$

(63)

Finally, when X _j (n − T ₁) remains small due to the scaling, ${\omega_{ij} (n_0) X_j(n-T_1) = \omega_{ij} (n_0) X_j(n_0) + {\mathcal{O}}(\eta)}$ (see Eq. (57)). Using this approximation and Eq. (47) once more, we can rewrite Eq. (63) as follows:

$$ \begin{aligned} Y_i(n) &= Y_i(n-T_1) \\ &+ {\frac{1-r^{T_1}}{1-k}} ( (1-k) Y_i(n_0) + \alpha X_i(n_0) - \theta_i - A_i )\\ &+ {\frac{1}{1-k}} \sum_{i \neq j} \left[\sum_{t=1}^{T_1} r^t \Uplambda_{ij} (n-t)\right] X_j(n-T_1) \\ &+ {\frac{r^{T_1}-1}{1-k}} ((1-k) Y_i(n-T_1) + \alpha X_i(n - T_1) - \theta_i - A_i)\\ &+ {{\mathcal{O}}}(\eta). \end{aligned} $$

(64)

By developing Eq. (64), we obtain Eq. (22).

Appendix 4: Macroscopic mean field approximation

A single population of neurons is considered for the following demonstration. Generalization to multiple populations is immediate. For simplicity, the refractoriness is included in the distribution of weights (α = ω _ii , and V _i (n) = ∑ _j ω _ij x _j (n)) and is thus assumed to be normally distributed. This approximation is possible so long as the refractoriness is of the same order of magnitude as μ_ω. Because weights are randomized at each time step n, for a given m, the local chaos hypothesis considered in this study is given as follows:

• 1. x _j (n) and $\mathit{\omega}_{ij}$ are independent ∀ i, j;

• 2. x _j (n) and x _i (n) are independent ∀ i ≠ j;

• 3. θ _i (n) and V _i (n) are independent ∀ i.

Internal states and activity are also random variables denoted by y _i and x _i , respectively, such that the system is a stochastic process. In the following, the mean of a random variable X belonging to the probability density function p _X is denoted by m(X), the variance, v(X), covariance of X and Y, cv(X, Y):

$$ m(X) = \int x p_X(x) dx; $$

(65)

$$ v(X) = \int x^2 p_X(x) dx - m(X)^2; $$

(66)

$$ cv(X,Y) = \int x y p_{X,Y} (x,y) dx dy - m(X)m(Y). $$

(67)

The mean of the internal states y _i and activity x _i are simply denoted y and x, respectively. By taking the mean over the neurons i in Eqs. (1)–(3), the mean of internal activity y is given as follows (using the hypotheses of independence described above and the law of large numbers):

$$ \begin{aligned} y (n+1) &= ky(n) + \sum_{j} m(\omega_{ij}x_j(n)) + \mu_{\theta}, \\ &= ky(n) + M m(\omega_{ij}) x(n) +\mu_{\theta}. \end{aligned} $$

(68)

The mean activity is given as follows:

$$ x(n) = \int u p_x(u) dx, $$

(69)

$$ =\int f(t) p_y(f(t)) dt \hbox { , by a change of variable }, $$

(70)

$$ =f\left({\frac{y(n)}{\sqrt{p^2 + v(y(n))}}}\right) \hbox { , for the particular}\, f\, \hbox{chosen (Amari 1971)}. $$

(71)

The variance of y _i is given as follows (using the hypotheses of independence described above):

$$ \begin{aligned} v(y(n+1)) &= k^2 v(y(n)) + Mv(\omega_{ij}x_j(n)) + \sigma_{\theta}^2 \\ &+ 2kcv(y_i(n),\theta_i). \end{aligned} $$

(72)

Note that by induction, y _i (n + 1) is also given as follows:

$$ y_i(n+1) = k^{n+1}y_i(0)+\sum_j\sum_{p=0}^n \omega_{ij}x_j(n-p) k^p+{\frac{1-k^{n+1}}{1-k}} \theta_i. $$

(73)

When the number of steps n is very large, this can be expressed as

$$ y_i(n+1) = \sum_j \omega_{ij} \tilde{x}_j(n) + {\frac{\theta_i}{1-k}}, $$

(74)

where $\tilde{x}_j(n) = \sum\nolimits_{p=0}^{n} x_j(n-p) k^p$. This term is also considered to be non-random as in Amari (1971). Therefore, Eq. (72) can be written as follows:

$$ \begin{aligned} v(y(n+1)) &= k^2 v(y(n)) + M (\mu_{\omega}^2v(x(n)) + x(n)^2 \sigma_{\omega}^2 + \sigma_{\omega}^2 v(x(n)) ) \\ &+ \sigma_{\theta}^2 + 2k {\frac{\sigma_{\theta^2}}{1-k}}. \end{aligned} $$

(75)

Because the mean and standard deviation of the weights decrease proportionally to ${\frac{1}{M}}$ when $M \rightarrow \infty ,$ the variance is given as follows:

$$ v(y(n+1)) = k^2 v(y(n)) + \sigma_{\theta}^2 {\frac{1+k}{1-k}}. $$

(76)

After a few time steps, the variance is constant, and is given as follows:

$$ v(y) = \sigma_{\theta}^2 {\frac{1}{(1-k)^2}}. $$

(77)

To validate the mean field approximation, we first verified the dependence of the variance of y(n) on $\sigma_{\mathit{\theta}},$ as shown at the top of Fig. 19. Different from Amari (1971) and Cessac et al. (1994), the mean field can also exhibit periodic/chaotic dynamics. There are thus two types of variations: one due to the mean-field dynamics (“macroscopic”) and another due to the randomness in the connectivity and threshold (“microscopic”). The two types of variation are dependent on the factor $\sigma_{\mathit{\theta}}$. To verify the validity of the mean field, we must quantify the distance between the trajectory of the mean of microscopic states and that of the macroscopic mean field approximation. In the bottom of Fig. 19, it is shown that as the number of neurons increases, the accuracy of the mean field approximation increases.

Fig. 19

Mean field approximation. a The standard deviation $\sqrt(v)$ of the internal states y _i (n) is proportional to σ_θ; the coefficient of proportionality (given by the slope of the linear regression) is equal to ${\frac{1}{1-k}},$ as described in Eq. (77). b Distance S between the mean of the microscopic internal states and the macroscopic mean field approximation for increasing number of neurons M. As M increases, the approximation becomes more accurate

The mean field approximation is generalized to two populations of neurons having the same variances of weights and thresholds, but different mean weights due to LTP/LTD, which leads to Eq. (29).