Dynamics of a Producer–Grazer Model Incorporating the Effects of Excess Food Nutrient Content on Grazer’s Growth

Abstract

Modeling under the framework of ecological stoichiometric allows the investigation of the effects of food quality on food web population dynamics. Recent discoveries in ecological stoichiometry suggest that grazer dynamics are affected by insufficient food nutrient content (low phosphorus (P)/carbon (C) ratio) as well as excess food nutrient content (high P:C). This phenomenon is known as the “stoichiometric knife edge.” While previous models have captured this phenomenon, they do not explicitly track P in the producer or in the media that supports the producer, which brings questions to the validity of their predictions. Here, we extend a Lotka–Volterra-type stoichiometric model by mechanistically deriving and tracking P in the producer and free P in the environment in order to investigate the growth response of Daphnia to algae of varying P:C ratios. Bifurcation analysis and numerical simulations of the full model, that explicitly tracks phosphorus, lead to quantitative different predictions than previous models that neglect to track free nutrients. The full model shows that the fate of the grazer population can be very sensitive to excess nutrient concentrations. Dynamical free nutrient pool seems to induce extreme grazer population density changes when total nutrient is in an intermediate range.

Appendices

Appendix 1: Remaining Cases for Proof of Theorem 3.1

Proof

Case 2: $x(t_1)=0$

Let $\overline{f}=f'(0)=\underset{x\rightarrow 0}{\lim }\frac{f(x)}{x}$ and $\overline{y}=\underset{t\in [0,t_1]}{\max }y(t) <\frac{P}{\theta }$. Then for every $t\in [0,t_1]$,

$$\begin{aligned} x'&= bx\min \left\{ 1-\frac{x}{k}, 1-\frac{q}{Q} \right\} -\min \left\{ f(x), \frac{\hat{f}\theta }{Q}\right\} y \\&\ge -f(x)y \ge -\bar{f}\bar{y}x \equiv \alpha x \end{aligned}$$

This implies that $x(t_1)\ge x(0)e^{\alpha t_1} > 0$, where $\alpha$ is a constant. This contradicts $x(t_1)=0$ and proves that $S(t_1)$ does not reach this boundary.

Case 3: $y(t_1)=0$

Then, for every $t\in [0,t_1]$,

$$\begin{aligned} y'&= \min \left\{ \hat{e}f(x),\frac{Q}{\theta }f(x),\hat{e}\hat{f}\frac{\theta }{Q}\right\} y-\hbox {d}y \\&\ge -\hbox {d}y. \end{aligned}$$

This implies that $y(t_1)\ge y(0)e^{-\hbox {d}t_1}>0$. This contradicts $y(t_1)=0$ and proves that $S(t_1)$ does not reach this boundary.

Case 4: $Qx+\theta y =P$

Since $v(P-Q(t_1)x(t_1)-\theta y(t_1))=0$

$$\begin{aligned} \frac{\hbox {d}(Qx+\theta y)}{\hbox {d}t}\bigg |_{t_1}&=Q'(t_1)x(t_1)+Q(t_1)x(t_1)'+\theta y'(t_1) \\&=-Q(t_1)\min \left\{ f(x(t_1)), \frac{\hat{f}\theta }{Q(t_1)}\right\} y(t_1)\\&\quad +\theta \min \left\{ \hat{e}f(x(t_1)), \frac{Q(t_1)}{\theta }f(x(t_1)), \hat{e}\hat{f}\frac{\theta }{Q(t_1)}\right\} y(t_1)-\theta \hbox {d}y(t_1) \\&= -y(t_1)\min \left\{ f(x(t_1)), \frac{\hat{f}\theta }{Q(t_1)}\right\} \left( Q(t_1)-\theta \min \left\{ \hat{e}, \frac{Q(t_1)}{\theta } \right\} \right) \\&-\theta \hbox {d}y(t_1) \le 0. \end{aligned}$$

Thus, $S(t_1)$ can not cross this boundary.

Case 5: $x(t_1)=K$

Then, for every $t\in [0,t_1]$,

$$\begin{aligned} x'&= bx\min \left\{ 1-\frac{x}{k}, 1-\frac{q}{Q} \right\} -\min \left\{ f(x), \frac{\hat{f}\theta }{Q}\right\} y \\&\le bx\min \left\{ 1-\frac{x}{k}, 1-\frac{q}{Q} \right\} \\&=bx\left( 1-\frac{x}{\min \left\{ k, \frac{Qx}{q}\right\} }\right) \\&\le bx\left( 1-\frac{x}{\min \left\{ k,\frac{P}{q} \right\} }\right) \\&= bx\left( 1-\frac{x}{K} \right) . \end{aligned}$$

Then, $x(t_1)\le K$ by a standard comparison argument, thus $S(t_1)$ can not cross this boundary.

Case 6: $Q(t_1)=\hat{Q}$

Since $v(P-Q(t_1)x(t_1)-\theta y(t_1),Q(t_1))=0$

$$\begin{aligned} Q'&=-b \min \left\{ Q(1.\frac{x}{k}), Q-q\right\} \\&<0.\\ \end{aligned}$$

Thus, $S(t_1)$ can not cross this boundary.$\square$

Appendix 2: Proof of Theorem 3.2

Proof

To prove that $E_0$ is unstable, it is sufficient to show the system linearized at this equilibrium has an eigenvalue whose real part is positive. This is seen in the following Jacobian,

$$\begin{aligned} J(E_0) = \left| \begin{array}{ccc} b\left( 1-\frac{q}{Q_0}\right) &{} 0 &{} 0 \\ 0 &{} G(0,0,Q_0) &{} 0 \\ H_x(0,0,Q_0) &{} H_y(0,0,Q_0) &{} H_Q(0,0,Q_0)\end{array} \right| , \end{aligned}$$

where $b\left( 1-\frac{q}{Q_0}\right) >0$.$\square$

Appendix 3: Proof of Lemma 3.1

Proof

We consider two cases ($1-\frac{x}{k}<1-\frac{q}{Q}$ and $1-\frac{x}{k}>1-\frac{q}{Q}$).

Case 1: $1-\frac{x}{k}<1-\frac{q}{Q}$

In this case, (Eq. 15a) becomes

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=bx\left( 1-\frac{x}{k}\right) -\min \left\{ f(x),\frac{\hat{f}\theta }{Q}\right\} y \end{aligned}$$

(21)

and $x_1=k$. (Eq. 15c) becomes

$$\begin{aligned} \frac{\hbox {d}Q}{\hbox {d}t}=v(P-Qx-\theta y, Q)-bQ\left( 1-\frac{x}{k}\right) \end{aligned}$$

(22)

therefore, $v(P-Q_1k, Q_1)=0$. There are two cases to consider here ($\frac{P}{k}>\hat{Q}$ and $\frac{P}{k}<\hat{Q}$ ). If $\frac{P}{k}>\hat{Q}$, then $Q_1=\hat{Q}$ to remain in $\Omega$. Since $P\ge Q_1x_1=Q_1k$, the case when $\frac{P}{k}<\hat{Q}$ results in $\hat{Q}>\frac{P}{k}\ge Q_1$, thus $Q_1=\frac{P}{k}$. The two cases are summarized below

$$\begin{aligned} Q_1 = \left\{ \begin{array}{ll} \hat{Q}&{} \text{ if } \frac{P}{k}> \hat{Q}\\ \frac{P}{k} &{} \text{ if } \frac{P}{k}< \hat{Q}\end{array} \right\} =\min \left\{ \frac{P}{k},\hat{Q}\right\} . \end{aligned}$$

(23)

Case 2: $1-\frac{x}{k}>1-\frac{q}{Q}$ In this case, (Eq. 15a) becomes

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=bx\left( 1-\frac{q}{Q}\right) -\min \left\{ f(x),\frac{\hat{f}\theta }{Q}\right\} y \end{aligned}$$

(24)

and $Q_1=q$. (Eq. 15c) becomes

$$\begin{aligned} \frac{\hbox {d}Q}{\hbox {d}t}=v(P-Qx-\theta y, Q)-bQ\left( 1-\frac{q}{Q}\right) \end{aligned}$$

(25)

therefore $v(P-qx_1, q)=0$ and thus $x_1=\frac{P}{q}$.

To show that the two equilibrium forms cannot coexist, we need to show that they satisfy two opposite conditions.

In case 1: $1-\frac{x}{k}<1-\frac{q}{Q}$ and $E_1=\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right)$, therefore

$$\begin{aligned} 0&<1-\frac{q}{\min \left\{ \frac{P}{k},\hat{Q}\right\} }\\ \implies&\min \left\{ \frac{P}{k},\hat{Q}\right\} >q. \end{aligned}$$

Here

$$\begin{aligned} \frac{P}{k}\ge \min \left\{ \frac{P}{k},\hat{Q}\right\} >q. \end{aligned}$$

In case 2: $1-\frac{x}{k}>1-\frac{q}{Q}$ and $E_1=\left( \frac{P}{q},0,q\right)$, therefore

$$\begin{aligned}&1-\frac{P}{qk}>0\\ \implies&\frac{P}{k}<q. \end{aligned}$$

The two cases follow opposite conditions. Actually, when $\frac{P}{k}=q$, the two forms of $E_1$ collide to $(k,0,q)$.$\square$

Appendix 4: Proof of Theorem 3.3

Proof

Assume that $\min \left\{ \hat{e}f(x_1),\frac{Q_1}{\theta }f(x_1),\hat{e}\hat{f}\frac{\theta }{Q_1}\right\} <d$. To prove that $E_1$ is stable, we consider two cases ($1-\frac{x}{k}<1-\frac{q}{Q}$ and $1-\frac{x}{k}>1-\frac{q}{Q}$) where we look at the linearized system and use the Routh–Hurwitz criterion.

Case 1: $1-\frac{x}{k}<1-\frac{q}{Q}$

Here, $E_1=\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right)$ by Lemma 3.1 and the Jacobian takes the following form,

$$\begin{aligned} J(E_1) = \left| \begin{array}{ccc} -b &{} kF_y\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} 0 \\ 0 &{} \min \left\{ \hat{e}f(k),\frac{\min \left\{ \frac{P}{k},\hat{Q}\right\} }{\theta }f(k),\hat{e}\hat{f}\frac{\theta }{\min \left\{ \frac{P}{k},\hat{Q}\right\} }\right\} -d &{} 0 \\ H_x\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} H_y\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} \frac{\hbox {d}v}{\hbox {d}Q} \big |_{E_1} \end{array} \right| . \end{aligned}$$

Let $\alpha _1 = \min \left\{ \hat{e}f(k),\frac{\min \left\{ \frac{P}{k},\hat{Q}\right\} }{\theta }f(k),\hat{e}\hat{f}\frac{\theta }{\min \left\{ \frac{P}{k},\hat{Q}\right\} }\right\} -d<0$ and $\alpha _2 = \frac{\hbox {d}v}{\hbox {d}Q} \big |_{E_1}<0$. Then, the Jacobian simplifies to

$$\begin{aligned} J(E_1) = \left| \begin{array}{ccc} -b &{} kF_y\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} 0 \\ 0 &{} \alpha _1 &{} 0 \\ H_x\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} H_y\left( k,0,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right) &{} \alpha _2 \end{array} \right| . \end{aligned}$$

The characteristic equation may be written

$$\begin{aligned} (-b-\lambda )(\alpha _1-\lambda )(\alpha _2-\lambda )=0 \end{aligned}$$

The eigenvalues of $J(E_1)$ are $-b, \alpha _1, \alpha _2$, which are all negative.

Case 2: $1-\frac{x}{k}>1-\frac{q}{Q}$

Here, $E_1=(\frac{P}{q},0,q)$ by Lemma 3.1 and the Jacobian takes the following form,

$$\begin{aligned} J(E_1) = \left| \begin{array}{ccc} 0 &{} \frac{P}{q}F_y(\frac{P}{q},0,q) &{} \frac{Pb}{q^2} \\ 0 &{} \min \left\{ \hat{e}f(\frac{P}{q}),\frac{\hat{q}}{\theta }f(\frac{P}{q}),\hat{e}\hat{f}\frac{\theta }{q}\right\} -d &{} 0 \\ \frac{\hbox {d}v}{\hbox {d}x}\big |_{E_1}&{} H_y(\frac{P}{q},0,q) &{} \frac{\hbox {d}v}{d\hbox {Q}}\big |_{E_1}-b \end{array} \right| . \end{aligned}$$

Let $\alpha _1=\min \left\{ \hat{e}f(\frac{P}{q}),\frac{\hat{q}}{\theta }f(\frac{P}{q}),\hat{e}\hat{f}\frac{\theta }{q}\right\} -d<0$, $\alpha _2=\frac{\hbox {d}v}{\hbox {d}Q}\big |_{E_1}-b<0$, $\alpha _3=\frac{\hbox {d}v}{\hbox {d}x}\big |_{E_1}<0$. Then the Jacobian simplifies down to

$$\begin{aligned} J(E_1) = \left| \begin{array}{ccc} 0 &{} \frac{P}{q}F_y(\frac{P}{q},0,q) &{} \frac{Pb}{q^2} \\ 0 &{} \alpha _1 &{} 0 \\ \alpha _3 &{} H_y(\frac{P}{q},0,q) &{} \alpha _2 \end{array} \right| . \end{aligned}$$

The characteristic equation may be written

$$\begin{aligned} \lambda ^3+\lambda ^2(-\alpha _1-\alpha _2)+\lambda (\alpha _1\alpha _2-\frac{Pb}{q^2}\alpha _3)+\frac{Pb}{q^2}\alpha _1\alpha _3. \end{aligned}$$

Since $\alpha _1, \alpha _2,\alpha _3<0$ we find that $-\alpha _1-\alpha _2>0$, $\frac{Pb}{q^2}\alpha _1\alpha _3>0$, and $(-\alpha _1-\alpha _2)(\alpha _1\alpha _2-\frac{Pb}{q^2}\alpha _3)>\frac{Pb}{q^2}\alpha _1\alpha _3$. These are the conditions of the Routh–Hurwitz criterion that guarantee all the eigenvalues of $J(E_1)$ have strictly negative real parts. Thus, $E_1$ is locally asymptotically stable for both cases.$\square$

Appendix 5: Proof of Theorem 3.4

Proof

The set $\Omega$ is positively invariant under System (15) by Lemma 3.1. Let

$$\begin{aligned} \alpha = \min \left\{ \hat{e}f(K),\frac{\hat{Q}}{\theta }f(K),\hat{e}\hat{f}\frac{\theta }{q}\right\} -d<0. \end{aligned}$$

(26)

For all $(x,y,Q)\in \Omega$, the expression for $y'$ may be expressed as

$$\begin{aligned} \frac{y'}{y}&=\min \left\{ \hat{e}f(x),\frac{Q}{\theta }f(x),\hat{e}\hat{f}\frac{\theta }{Q}\right\} -d \\&\le \min \left\{ \hat{e}f(K),\frac{\hat{Q}}{\theta }f(K),\hat{e}\hat{f}\frac{\theta }{q}\right\} -d \\&= \alpha \end{aligned}$$

This implies that $\underset{t \rightarrow \infty }{\lim }y(t)=0$. In autonomous System (15), $y(t)$ converges to 0. We may consider the behavior of System (15) on the plane $y=0$ with the limit system

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}&= bx \min \left\{ 1-\frac{x}{k}, 1-\frac{q}{Q} \right\} \end{aligned}$$

(27a)

$$\begin{aligned} \frac{\hbox {d}Q}{\hbox {d}t}&= v(P-Qx,Q)-b\min \left\{ Q(1-\frac{x}{k}), (Q-q)\right\} , \end{aligned}$$

(27b)

defined on the domain

$$\begin{aligned} \bar{\Omega }=\left\{ (x,Q) | 0<x< K , q<Q<\hat{Q}\right\} \end{aligned}$$

(28)

System (27) is the limiting system of the asymptotically autonomous System (15) under the constraint $\min \left\{ \hat{e}f(K),\frac{\hat{Q}}{\theta }f(K),\hat{e}\hat{f}\frac{\theta }{q}\right\} -d$. Results from Markus (1956) and Thieme (1992) allow us to compare solutions of an autonomous system with those of the asymptotically autonomous limit system. System (27) has one equilibrium $\bar{E}_1 = (\bar{x}_1, \bar{Q}_1)$, and this equilibrium is globally asymptotically stable. To show this global stability, we consider two cases ($1-\frac{x}{k}<1-\frac{q}{Q}$ and $1-\frac{x}{k}>1-\frac{q}{Q}$) where we look at the linearized system and then consider the existence of periodic orbits.

Case 1: $1-\frac{x}{k}<1-\frac{q}{Q}$

Here, $\bar{E_1}=\left( k,\min \left\{ \frac{P}{k},\hat{Q}\right\} \right)$ and the Jacobian takes the form,

$$\begin{aligned} J(\bar{E}_1) = \left| \begin{array}{cc} -b &{} 0 \\ \frac{\hbox {d}v}{\hbox {d}x} \big |_{\bar{E_1}}+\frac{b\min \left\{ \frac{P}{k},\hat{Q}\right\} }{k} &{} \frac{\hbox {d}v}{\hbox {d}Q}\big |_{\bar{E_1}}\end{array} \right| . \end{aligned}$$

The eigenvalues are $-b<0$ and $\frac{\hbox {d}v}{\hbox {d}Q}\big |_{\bar{E_1}}<0$.

Case 2: $1-\frac{x}{k}>1-\frac{q}{Q}$

Here, $\bar{E_1}=(\frac{P}{q},q)$ and the Jacobian takes the form,

$$\begin{aligned} J(\bar{E}_1) = \left| \begin{array}{cc} 0 &{} b\frac{P}{q^2} \\ \frac{\hbox {d}v}{\hbox {d}x}\big |_{\bar{E_1}} &{} \frac{\hbox {d}v}{\hbox {d}Q}\big |_{\bar{E_1}}-b\end{array} \right| . \end{aligned}$$

Here, trace$(J(\bar{E}_1))=\frac{\hbox {d}v}{\hbox {d}Q}\big |_{\bar{E_1}}-b<0$ and det$(J(\bar{E}_1))= -b\frac{P^2}{q^2}\frac{\hbox {d}v}{\hbox {d}x}\big |_{\bar{E_1}}>0$. In both cases, $\bar{E}_1$ is locally asymptotically stable. To show that no periodic orbits exist in $\bar{\Omega }$, consider

$$\begin{aligned} (xQ)'=xv(P-Qx, Q)>0. \end{aligned}$$

Therefore, there is no $t_1$ such that $Q'(t_1)<0$ and $x'(t_1)<0$; hence, there can not be any periodic solutions. Since $\bar{\Omega }$ is simply connected and is positively invariant under System (27) and contains no periodic orbits, by the Poincaré–Bendixson Theorem, all solutions of System (27) starting in $\bar{\Omega }$ will converge to $\bar{E}_1$. Thus, $\bar{E}_1$ is globally asymptotically stable. The $\omega -$limit set of a forward bounded solution of the autonomous System (15) consists of the equilibrium of its limit autonomous System (27) (Thieme 1992). Thus, the $\omega -$limit set of System (15) is $\{{E}_1\}$. The grazer only extinction equilibrium $E_1$ is globally asymptotically stable,

$$\begin{aligned}&\hbox {if }1-\frac{x}{k}<1-\frac{q}{Q}\quad \hbox {then} \quad \underset{t \rightarrow \infty }{\lim }(x(t),y(t),Q(t))=\left( k, 0, \min \left\{ \frac{P}{k}, \hat{Q} \right\} \right) ,\\&\hbox {if }1-\frac{x}{k}>1-\frac{q}{Q} \quad \hbox {then} \quad \underset{t \rightarrow \infty }{\lim }(x(t),y(t),Q(t))=\left( \frac{P}{q}, 0, q\right) . \end{aligned}$$

$\square$

Appendix 6: Supplementary Material Notes

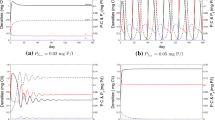
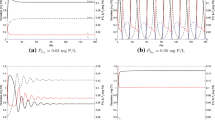
An animation of the three dimensional phase space is provided in the supplementary material. The animation was created using MATLAB. Here, we used the Holling-type II function $f(x)=\frac{\hat{f}x}{a+x}$ for the grazer ingestion rate and the parameter values listed in Table 1 and P varying from 0.001 to 0.14 mg P/L. The surfaces are the producer (blue), grazer (yellow), and producer P:C (red) nullsurfaces. The intersections of these surfaces depict equilibria. The equilibria that simulations suggest are stable are labeled with black dots; equilibria that simulations suggest are unstable are labeled with white dots.