An Exactly Solvable Model of Random Site-Specific Recombinations

Abstract

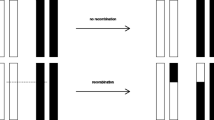
Cre-lox and other systems are used as genetic tools to control site-specific recombination (SSR) events in genomic DNA. If multiple recombination sites are organized in a compact cluster within the same genome, a series of random recombination events may generate substantial cell specific genomic diversity. This diversity is used, for example, to distinguish neurons in the brain of the same multicellular mosaic organism, within the brainbow approach to neuronal connectome. In this paper, we study an exactly solvable statistical model for SSR operating on a cluster of recombination sites. We consider two types of recombination events: inversions and excisions. Both of these events are available in the Cre-lox system. We derive three properties of the sequences generated by multiple recombination events. First, we describe the set of sequences that can in principle be generated by multiple inversions operating on the given initial sequence. We call this description the ergodicity theorem. On the basis of this description, we calculate the number of sequences that can be generated from an initial sequence. This number of sequences is experimentally testable. Second, we demonstrate that after a large number of random inversions every sequence that can be generated is generated with equal probability. Lastly, we derive the equations for the probability to find a sequence as a function of time in the limit when excisions are much less frequent than inversions, such as in shufflon sequences.

Appendix: Constrained Inversions

In this section, we generalize the results obtained in Sects. 2 and 3 to systems in which inversions can happen between inverted SSR-sites (RL), but not between matching SSR-sites (LR) (Komano, personal communications). We call this type of recombination, when only one type of inversions is possible, the case of constrained inversions. As before, we assume the DNA sequence starts with an R and ends with an L SSR-site. Here, we will show that most of the results obtained in the present study can apply in the case of constrained inversions. However, some of sequences cannot be obtained due to the constraint, as detailed below.

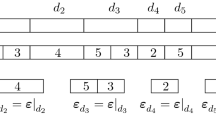
Before we present our results, we will illustrate the effects of the constraint on a simple example (Fig. 15). This sequence has M=0 LL or RR sites, and N=3 LR or RL sites. Equation (2) yields $Z_{M,N} = 2^{N}M! [\frac{N + 1}{2}]! [\frac{N}{2}]!d_{(M,N)} = 16$ sequences. Here, as above, [x] means the largest integer smaller than or equal to x. However, as illustrated in Fig. 15, only 8 of these sequences can be reached using the constrained inversions. We show here that this result is general, i.e., with the constrained inversion, the number of possible sequences in always equal to one-half of that for the case of all inversions possible:

$$ Z_{M,N}^{\mathrm{constrained}} = 2^{N - 1}M! \biggl[ \frac{{N + 1}}{2}\biggr]! \biggl[\frac{{N}}{2}\biggr]!d_{(M,N)}. $$

(15)

Here, d _(M,N) is given in Eq. (1).

Fig. 15

Constrained inversions. (A) An initial sequence. (B) Sequences that can be obtained from (A) using inversions between RL, but not LR sites. (C) Sequences that cannot be obtained from (A) with the constrained inversions

Below we will sketch the proof of Eq. (15). Let us consider a DNA sequence that includes two LR units. It can be written as follows: <A<B>C<D>E<. Here, <B> and <D> are LR, while other units can contain arbitrary combinations of units as well. <B> and <D> cannot be inverted individually without the affecting rest of the sequence. It is easy to check by enumeration of all possible inversions that impossible combinations satisfy a simple constraint. Let us introduce the number of reverse-compliments amongst LR units w.r.t. the initial orientation, t. Thus, for the sequence >A<D′>C<B>E< (<D′> means reverse-complement of <D>), t=1. Let us also introduce the number s, which is the number of exchanges in the <B> and <D> pair. For the sequence >A<D′>C<B>E<, s=1, while for >A<B′>C<D′>E<, s=0. It is possible to check that only the sequences for which s+t is even can be obtained from the initial sequence >A<B>C<D>E<. The sequences for which s+t is odd are not possible through the constrained inversions. This is only true for the fixed remainder of the sequence, i.e., >A<^∗>C<^∗> E<. Here, ‘^∗’ denotes either B or D or their reverse-complement. We therefore call the number χ=s+t the index of sequence. One can obtain >A<^∗>C<^∗>E< from >A<B>C<D>E< if χ (>A<e^∗>C<^∗>E<) is even.

Let us now consider the sequence with more than two LR elements >A<B>C<D>E<⋯>Z<. A set of sequences within LR units can be obtained by a permutation P of the original sequence. Permutations form a group of transformations called the symmetric group. Every permutation can be written as a product of several neighboring exchanges. The permutation is called even or odd if it can be written as a product of an even/odd number of neighboring exchanges. Even/odd permutations will be assigned index s equal to 0 or 1, respectively. Although there are several ways to implement P as a superposition of neighboring exchanges, they all have the same index s. The number of reverse complement LR elements can be defined as above, as well as the index χ=s+t. We showed above that a possible exchange does not change the evenness of index χ. Thus, impossible configurations are such that index χ is odd, because the original configuration has an even index. Because for unconstrained inversions both even and odd χ are possible for the same fixed residual sequence, the number of configurations is reduced by a factor of 2 in the case of constrained inversions. Therefore, Eq. (15) describes the number of configurations in the constrained case. This describes the modifications to Theorem 2.

It is possible to show that in the case of constrained inversions, Properties 1–4 and Theorem 1 still hold. In the proof of Theorem 1, the first step remains the same while in the second step, we use the operation I=(c,e)(a,c) shown in Fig. 16.

Fig. 16

Operation involving inversions only between RL SSR-sites that corresponds to Type-B inversion in the proof of Theorem 1

Theorem 3 holds as before, therefore, we still have equal probability to observe all possible DNA sequences included in Eq. (15).