1 Introduction

Study of wave–seabed interaction is essential to offshore developments. There are a few characteristics on loading conditions on seabed soil, and one of them is that the soil is subject to considerable principal stress rotation (PSR). Ishihara and Towhata [6] first proposed that the PSR can generate plastic deformation and non-coaxiality even without a change in principal stress magnitudes under wave loadings. Continuous PSR can also generate excess pore water pressure and cumulative shear strain in undrained condition. Similar studies are also carried out by Ishihara and Yamazaki [7], Bhatia et al. [2], Miura et al. [11], Gutierrez et al. [5], Yang and Yu [17], and Yang and Yu [18]. Because the plastic deformation caused by the PSR from the wave loading can accelerate undrained soil liquefaction, ignoring this PSR-induced deformation may lead to unsafe design. Due to the significance of the PSR in seabed soil, a few experimental studies have been carried out to study it. For instance, Nago and Maeno [12] and Zen et al. [20] investigated the behavior of cohesionless sediments subjected to oscillatory pore pressure with large-scale model in 1-g condition. Sassa and Sekiguchi [13] also carried out a series of centrifuge wave tests on seabeds with fine-grained sand. They found that the soil behaviors are greatly affected by the PSR under the wave loading. They also proposed the concept of critical cyclic stress ratio below which the liquefaction will not occur.

Although researchers have recognized the importance of the PSR in seabed soil and conducted extensive experimental studies, there are few considerations of the PSR impact on numerical simulations of wave–seabed soil interactions. Only a few studies can be found in Dunn et al. [4], Li and Jeng [9], and Liu et al. [10]. One of the best known researches in this topic was the finite element simulation conducted by Sassa and Sekiguchi [14]. They implemented a cyclic loading elastoplastic soil model into the finite element analysis to study wave–seabed interaction under both progressive and standing waves. They compared the simulation results with the experimental data and found that the sand bed is less resistant to the liquefaction if the PSR is considered in the soil model. However, Jeng [8] claims that Sassa’s model has several limitations in the simulation of this kind of problems, such as the lack of consideration of viscosity and the assumption of infinite bed. One of them is that the simulation results from this PSR model seem to be very sensitive to the model parameters, which restricts its application.

This paper aims to take into account the impacts of PSR in the numerical simulations of wave–seabed interactions by using a well-established PSR soil model. This model is developed on the basis of kinematic hardening principle with bounding surface concept and critical state concept. It can consider the PSR effect by treating the stress rate generating the PSR independently [19], and the simulation results demonstrate that this model has great ability to simulate the PSR effects in single-element studies. The focus of the paper is on the investigation of the PSR impact on the boundary value problems of wave–seabed interactions. Firstly, the original model and the PSR model will be introduced. Secondly, these two models will be tested in a single-element numerical simulation. Finally, they will be implemented into the finite element software to simulate centrifuge tests of wave–seabed interactions by Sassa and Sekiguchi [13], and the simulation results will be compared with experimental results.

2 The original soil model

2.1 Model formulations

A well-established soil model with bounding surface concept and kinematic hardening is chosen as the base model. It employs the back-stress ratio as the hardening parameter and the state parameter to represent influences of different confining stresses and void ratios on sand behaviors. It also adopts the critical state concept and phase transformation line. However, it does not give special consideration of the PSR effect. This model will be briefly introduced, and more details about this model can be found in Dafalias and Manzari [3].

The yield function of the model is

$$f \, = \left[ {\left( {{\mathbf{s}} - \, p{\varvec{\upalpha}}} \right) \, : \, \left( {{\mathbf{s}} - \, p{\varvec{\upalpha}}} \right)} \right]^{1/2} - \sqrt {2/3} pm \, = 0$$
(1)

where s is the deviatoric stress tensor. P and α are the confining pressure and back-stress ratio tensor, respectively. α represents the center of yield surface in the stress ratio space while m is the radius of yield surface, and m is assumed to be a small constant, indicating no isotropic hardening. The normal to the yield surface is defined as:

$${\mathbf{I}} = \frac{\partial f}{{\partial {\varvec{\upsigma}}}} = {\mathbf{n}} - \frac{1}{3}\left( {{\mathbf{n}}:{\mathbf{r}}} \right){\mathbf{I}};{\mathbf{n}} = \frac{{{\mathbf{r}} - {\varvec{\upalpha}}}}{{\sqrt {2/3} m}}$$
(2)

where I is the isotropic tensor and n represents the normal to the yield surface on the deviatoric plane. r represents the stress ratio and is equal to s/p. The elastic shear strain rate is a function of elastic shear modulus and bulk modulus, which are dependent on the confining pressure. The plastic strain rate \(d{\varvec{\upvarepsilon}}^{p}\) is defined as:

$$d{\varvec{\upvarepsilon}}^{p} = \left\langle L \right\rangle \,{\mathbf{R}}$$
(3)
$$L = \frac{1}{{K_{\text{p}} }}\left( {\frac{\partial f}{{\partial {\varvec{\upsigma}}}}} \right):{\text{d}}{\varvec{\upsigma}}$$
(4)
$${\mathbf{R}} = {\mathbf{n}} + \frac{1}{3}D{\mathbf{I}}$$
(5)

where L represents the plastic multiplier (or loading index), and R is the normal to the potential surface, indicating the direction of the plastic strain rate. I is the isotropic tensor, and n represents the normal to the yield surface on the deviatoric plane. K p is the plastic modulus, and D is the dilatancy ratio, and they are defined as:

$$K_{\text{p}} = \frac{2}{3}p\left[ {G_{0} h_{0} (1 - c_{h} e)\left( {\frac{p}{{p_{\text{at}} }}} \right)^{ - 1/2} } \right]\left[ {\frac{{\left| {{\mathbf{b:n}}} \right|}}{{\left| {({\varvec{\upalpha}} - {\varvec{\upalpha}}_{\text{in}} ){\mathbf{:n}}} \right|}}} \right]$$
(6)
$$D = A_{d} {\mathbf{d:n}}$$
(7)

where b and d are the distances between the current back-stress ratio tensor and bounding and dilatancy back-stress ratio tensors, respectively. h 0 , c h , and A d are the model parameters. α in is the initial value of α at the start of a new loading process and is updated when the denominator becomes negative.

2.2 Model simulations of laboratory experiments

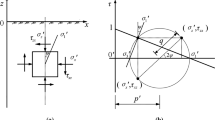
A series of drained monotonic loading tests on Leighton Buzzard sand (Fraction B) with different loading directions (α = 0°–90°) and drained pure rotational shear tests with different stress ratios [16] are simulated by using the original model. These tests were conducted in NCG at the University of Nottingham using the hollow cylinder apparatus, and the stress paths of these tests are illustrated in Fig. 1. The model parameters are listed in Table 1. Figure 2 shows the comparison between the predicted results and the laboratory results under monotonic loading, and the compression is negative. Because this model does not consider the effect of fabric anisotropy of the sand, the results are intended to fit the average of the laboratory results. These results verify the ability of this model in simulating soil behaviors under the monotonic loading path. The results of the pure rotational loadings are shown in Fig. 3, and q represents the deviatoric stress while p′ represents the effective confining stress. It can be seen that the original model significantly underestimates the volumetric strain in the case of q/p′ = 0.93 and 0.9, while it significantly overestimates the volumetric strain in the case of q/p′ = 0.8, 0.7, and 0.6. This is mainly because the original model does not give special consideration to the PSR. To better simulate this problem, a new model is developed based on the original model by separately considering the PSR.

Fig. 1
figure 1

Stress paths of monotonic loading (a) and pure rotational loading (b) (after [16]

Full size image
Table 1 Soil parameters of Leighton Buzzard sand used in the finite element analysis
Full size table
Fig. 2
figure 2

Comparison between the predicted results and laboratory results under the monotonic loading a stress ratio, b volumetric strain (tension: positive)

Full size image
Fig. 3
figure 3

Comparison of volumetric strain developments between the predicted results and laboratory results under the drained pure rotational loading (tension: +ve) (a stress ratio 0.6–0.8; b stress ratio 0.9–0.93)

Full size image

3 The PSR modified soil model

In the PSR modified model, the plastic strain rate is split into the monotonic strain rate \(d{\varvec{\upvarepsilon}}_{m}^{p}\) and the PSR strain rate \(d{\varvec{\upvarepsilon}}_{r}^{p}\), where the subscripts m and r represent monotonic and PSR loading hereinafter, respectively. The evolution of hardening parameter is not affected by this separate treatment. Therefore, the plastic strain rate can be expressed as:

$$d{\varvec{\upvarepsilon}}_{m}^{p} = \left\langle {L_{m} } \right\rangle \,{\mathbf{R}}_{m} = \frac{1}{{K_{pm} }}\left( {\frac{{\partial \text{ }f}}{{\partial \text{ }{\varvec{\upsigma}}}}{\text{d}}{\varvec{\upsigma}}_{m} } \right){\mathbf{R}}_{m}$$
(8)
$$d{\varvec{\upvarepsilon}}_{r}^{p} = \left\langle {L_{r} } \right\rangle \,{\mathbf{R}}_{r} = \frac{1}{{K_{pr} }}\left( {\frac{{\partial \text{ }f}}{{\partial \text{ }{\varvec{\upsigma}}}}{\text{d}}{\varvec{\upsigma}}_{r} } \right){\mathbf{R}}_{r}$$
(9)

It is assumed that K pm  = K p and R m = R (Eqs. 5, 6) because the original model is for non-PSR loading. The direction of PSR strain rate R r can be expressed as:

$${\mathbf{R}}_{r} = {\mathbf{n}}_{r} + \frac{1}{3}D_{r} {\mathbf{I}}$$
(10)

where n r is the direction of deviatoric plastic strain rate and can be approximated as n for simplicity. D r is the dilatancy ratio for the PSR loading rate, and it can be derived from the postulate of the PSR dilatancy ratio [5] and expressed as:

$$D_{r} = A_{r} \left( {1 - \alpha /\alpha_{\theta }^{b} } \right)\alpha$$
(11)

where A r is a constant for the impact of PSR on the dilatancy. The plastic modulus K pr for PSR loading rate is defined as:

$$K_{pr} = \frac{2}{3}p\,\left[ {G_{0} h_{0r} (1 - c_{h} e)\left( {\frac{p}{{p_{at} }}} \right)^{ - 1/2} } \right]\left( {\frac{{\left| {{\mathbf{b}}:{\mathbf{n}}} \right|}}{{\left| {({\varvec{\upalpha}} - {\varvec{\upalpha}}_{in} ):{\mathbf{n}}} \right|}}} \right)^{{\xi_{r} }}$$
(12)

where h 0r and ξ r are new model parameters associated with the PSR. In order to make K pr more sensitive to the stress ration, ξ r is usually larger than unity.

At present, all new parameters for the modified model are introduced. Finally, to complete the model, the definition of PSR loading rate dσ r is required. To determine dσ r in general stress space, it is first considered in the space with only x- and y-directions denoted as α. It can be expressed as \({\text{d}}{\varvec{\upsigma}}_{r}^{\alpha } = {\mathbf{N}}_{r}^{\alpha } {\text{d}}{\varvec{\upsigma}}\) and then in matrix form as:

$$\left( {\begin{array}{*{20}c} \begin{aligned} {\text{d}}\sigma_{rx}^{\alpha } \hfill \\ \hfill \\ \end{aligned} \\ \begin{aligned} {\text{d}}\sigma_{ry}^{\alpha } \hfill \\ \hfill \\ {\text{d}}\sigma_{rxy}^{\alpha } \hfill \\ \end{aligned} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\frac{1}{2} - \frac{{(\sigma_{x} - \sigma_{y} )^{2} }}{{8t_{J}^{\alpha } }}} & { - \frac{1}{2} + \frac{{(\sigma_{x} - \sigma_{y} )^{2} }}{{8t_{J}^{\alpha } }}} & { - \frac{{(\sigma_{x} - \sigma_{y} )\,\sigma_{xy} }}{{2t_{J}^{\alpha } }}} \\ { - \frac{1}{2} + \frac{{(\sigma_{x} - \sigma_{y} )^{2} }}{{8t_{J}^{\alpha } }}} & {\frac{1}{2} - \frac{{(\sigma_{x} - \sigma_{y} )^{2} }}{{8t_{J}^{\alpha } }}} & {\frac{{(\sigma_{x} - \sigma_{y} )\,\sigma_{xy} }}{{2t_{J}^{\alpha } }}} \\ { - \frac{{(\sigma_{x} - \sigma_{y} )\,\sigma_{xy} }}{{4t_{J}^{\alpha } }}} & {\frac{{(\sigma_{x} - \sigma_{y} )\,\sigma_{xy} }}{{4t_{J}^{\alpha } }}} & {1 - \frac{{\sigma_{xy}^{2} }}{{t_{J}^{\alpha } }}} \\ \end{array} } \right]\;\left( {\begin{array}{*{20}c} \begin{aligned} {\text{d}}\sigma_{x} \hfill \\ \hfill \\ \end{aligned} \\ \begin{aligned} {\text{d}}\sigma_{y} \hfill \\ \hfill \\ \end{aligned} \\ {{\text{d}}\sigma_{xy} } \\ \end{array} } \right)$$
(13)

where \(t_{J}^{\alpha } = (\sigma_{x} - \sigma_{y} )^{2} /4 + \sigma_{xy}^{2}\). Similarly, in the \(\beta\) space (y, z) and \(\gamma\) space (z, x), they can be defined as \({\text{d}}{\varvec{\upsigma}}_{r}^{\beta } = {\mathbf{N}}_{r}^{\beta } {\text{d}}{\varvec{\upsigma}}\) and \({\text{d}}{\varvec{\upsigma}}_{r}^{\gamma } = {\mathbf{N}}_{r}^{\gamma } {\text{d}}{\varvec{\upsigma}}\).Combining \({\text{d}}{\varvec{\upsigma}}_{{\mathbf{r}}}^{\alpha }\), \({\text{d}}{\varvec{\upsigma}}_{{\mathbf{r}}}^{\beta }\), and \({\text{d}}{\varvec{\upsigma}}_{{\mathbf{r}}}^{\gamma }\), and letting \({\text{d}}\sigma_{rx} = {\text{d}}\sigma_{rx}^{\alpha } + {\text{d}}\sigma_{rx}^{\gamma }\), \({\text{d}}\sigma_{ry} = {\text{d}}\sigma_{ry}^{\alpha } + {\text{d}}\sigma_{ry}^{\beta }\), and \({\text{d}}\sigma_{rz} = {\text{d}}\sigma_{rz}^{\beta } + {\text{d}}\sigma_{rz}^{\gamma }\), \({\text{d}}{\varvec{\upsigma}}_{r}\) in the general stress space can be obtained as:

$${\text{d}}{\varvec{\upsigma}}_{r} = {\mathbf{N}}_{r} {\text{d}}{\varvec{\upsigma}}$$
(14)

The relationship between the stress and strain rates can be expressed as:

$${\text{d}}{\varvec{\upsigma}} = {\mathbf{E}}^{ep} {\text{d}}{\varvec{\upvarepsilon}}$$
(15)
$${\mathbf{E}}^{ep} = {\mathbf{E}} - B_{1} \left[ {\frac{{({\mathbf{ER}})({\mathbf{lN}}_{r}^{*} )}}{{K_{pr} + {\mathbf{lN}}_{r}^{*} {\mathbf{R}}_{r} }} - \frac{{({\mathbf{ER}})({\mathbf{lE}})}}{{K_{pr} + {\mathbf{lER}}_{r} }}} \right] - B_{2} \left[ {\frac{{({\mathbf{ER}}_{r} )({\mathbf{lN}}_{r}^{*} )}}{{{\mathbf{lN}}_{r}^{*} {\mathbf{R}}}} - \frac{{({\mathbf{ER}}_{r} )({\mathbf{lE}})}}{{K_{p} + {\mathbf{lER}}}}} \right]$$
(16)
$${\mathbf{N}}_{r}^{*} = 2G\,{\mathbf{N}}_{r}$$
(17)
$$B_{1} = \left( {\frac{{{\mathbf{lN}}_{r}^{*} {\mathbf{R}}}}{{K_{pr} + {\mathbf{lN}}_{r}^{*} {\mathbf{R}}_{r} }} - \frac{{K_{p} + {\mathbf{lER}}}}{{K_{pr} + {\mathbf{lER}}_{r} }}} \right)^{ - 1}$$
(18)
$$B_{2} = \left( {\frac{{K_{pr} + {\mathbf{lN}}_{r}^{*} {\mathbf{R}}_{r} }}{{{\mathbf{lN}}_{r}^{*} {\mathbf{R}}}} - \frac{{K_{pr} + {\mathbf{lER}}_{r} }}{{K_{p} + {\mathbf{lER}}}}} \right)^{ - 1}$$
(19)

where E denotes the elastic stiffness tensor. The above formulations show that the stiffness tensor is independent of stress increments, and the stress and strain increments have a linear relationship, which indicates the easy numerical implementations. In these equations, if K pr is set to be K p and R r to be R, they will be downgraded to the formulations in the classical plasticity.

The PSR modified model is used to simulate the above-mentioned laboratory tests. Figure 3 shows the simulations, compared with the simulations with the original model and test results. In the cases of q/p′ = 0.6, 0.7, and 0.8, the modified model generates less volumetric strain than the original model, which agrees much better with the test results. In the cases of q/p′ = 0.9 and 0.93 close to the failure stress ratio, while the original model significantly underestimates the volumetric strains, the modified model predicts much larger volumetric strains, agreeing better with the test results. Generally, the results from the modified model fit better with the test results than the original model under the PSR. The capability of the PSR modified model will be further verified by the finite element analysis of the following wave–seabed soil interactions.

4 Finite element analysis of wave–seabed interactions

4.1 Problem definition

The centrifuge experimental study carried out by Sassa and Sekiguchi [13] investigates the behaviors of sand bed such as its liquefaction, under fluid wave trains including the progressive wave and standing wave. These waves can generate the PSR in the seabed soil. In these centrifuge tests with plain strain conditions, a seabed with saturated sand is 100 mm deep and 200 mm wide, and it is subjected to the progressive and standing wave loading, shown in Fig. 4. A steady-state acceleration of 50g is applied to the centrifuge. The sand is loose Leighton Buzzard sand (Fraction E, 100/170).The progressive wave and the standing wave have the wavelength denoted by L and wave period by T. These two types of waves are defined by the pore pressure u0 on the soil surface (z = 0) as:

$$u \, = u_{0}\,{\sin }\left( {\kappa x - wt} \right)\quad \left( {\text{progressive wave}} \right)$$
(20)
$$u \, = u_{0} \cos \left( {\kappa x} \right)\sin \left( {wt} \right)\quad \left( {\text{standing wave}} \right)$$
(21)

where u 0 is the amplitude of the fluid pressure fluctuation imposed on the soil surface. κ is the wave number, and w is the angular frequency of the waves, and they are defined as:

$$\kappa = 2\pi /L$$
(22)
$$w \, = \, 2\pi /T$$
(23)

For the progressive wave loading, eight cases with different u 0 from 1 to 6 kPa are simulated, given in Table 2a. The intensity of the progressive wave is also represented by the cyclic stress ratio, χ 0 = κu 0 /γ′, where the saturated unit weight of soil γ′ is 425 kN/m3, and κ was 12.2 m−1 [14].The standing wave loadings with diverse cyclic stress ratios are given in Table 2b. Their antinodes are set at the middle of the seabed width.

Fig. 4
figure 4

Sand bed setup for the progressive (a) and standing wave loading (b) (after [13]

Full size image
Table 2 Cases analyzed for progressive wave loading (a) and standing wave loading (b)
Full size table

The problem is simulated by the finite element software which adopts the effective stress theory and Forchheimer’s law which is a rigorous format of Darcy’s flow law, and the acceleration is negligible in wave loading with relatively low frequencies. The soil model and two types of waves are implemented by using user subroutines. Generally, the same setting as in the finite element analysis by Sassa and Sekiguchi [14] is used in this simulation, including the coefficient of permeability of 0.0015 m/s, so as to compare the predicted results with their experimental and numerical studies. Quadrilateral elements with four nodes are used for the simulations. The bottom boundary is set to be fixed while the side boundaries are smooth vertically, and all of them are impermeable. All cases analyzed are assumed to be under K 0 condition before the wave loading is applied, and K 0 is set to be 0.52. Twenty-five cycles of wave loadings are considered in total. Furthermore, the numerical implementation of the PSR model is performed using an explicit substepping integration algorithm with automatic error controls. In this integration scheme, the imposed strain increment can be automatically divided based on the prescribed error tolerance and details can be found in Abbo [1].

The first 13 model parameters in the original model without the PSR for Leighton Buzzard sand (Fraction E, 100/170) are calibrated by using a series of triaxial tests with constant effective confining stress [15], and they are listed in Table 1. Some typical simulation results together with test results are shown in Fig. 5. This figure indicates that the predicted results generally fit the laboratory results very well. Those three PSR model parameters are basically calibrated to better fit the experimental results from the centrifuge wave tank tests, listed in Table 2.

Fig. 5
figure 5

Predicted results and laboratory results from drained triaxial tests with constant p′ for Leighton Buzzard sand (Fraction E), a deviatoric stress, b volumetric strains (100 and 200 confining pressure, C-compression, E-extension)

Full size image

4.2 Predictions under the progressive waves

Case P8 with the cyclic stress ratio χ 0 = 0.17 is studied first. Figure 6 shows the development of pore water pressure and change in effective confining pressure at point a in Fig. 4 in the centerline of the seabed with the depth of 15 mm. Only 19 cycles are recorded in the figure because the modified model has already brought the soil to liquefaction in the 19th cycle. It is proposed that the excess pore water pressure is divided into two parts:

$$u_{e} = u_{e}^{1} + u_{e}^{2}$$
(24)

where u 1 e is the oscillatory part and u 2 e is the residual part, taking the average of the moving wave u e . Unless specified otherwise, all pore water pressures presented in this paper are the residual pore water pressures. Figure 6a shows that a significant buildup of pore water pressure can be observed in the results from both the original model and modified model due to the plastic contractive behavior of sand under the cyclic loading. However, the modified model produces a higher pore water pressure in the whole process and finally reaches a pore water pressure of 6.0 kPa. This value is about 95 % of the initial vertical stress, indicating the occurrence of liquefaction. The original model achieves a maximum pore water pressure of 4.9 kPa, which is lower than the results by the modified model and the laboratory results, and does not reach the liquefaction. Generally, the modified model agrees better with the test results, especially for pore water pressure near the liquefaction. However, both models overestimate the pore water pressure during the early stage of the simulation. The same difference can be seen in the effective confining pressure p′ as well, in Fig. 6b. As the progressive wave repeatedly moves along the seabed surface, p′ continues to decrease from both original and modified model. But p′ from the modified model decreases more rapidly than the original model and finally reaches a value very close to zero as the pore water pressure reaches the maximum value. In the original model, p′ reaches the lowest value of 0.75 kPa, indicating no liquefaction, and the trend becomes flatter after 2 s. Figure 7 shows the predicted stress path of σ 13 and (σ 1–σ 3)/2 by using the original model, which is also similar to the stress path by using the modified model. It shows that the principal stress continuously rotates under the progressive wave. The PSR is more profound with increasing number of progressive wave, where the normal stress difference becomes smaller. It can explain that the predicted pore water pressure by using the original and modified models becomes larger with increasing number of waves, and only the modified model considering the PSR brings soil to liquefaction at the end.

Fig. 6
figure 6

Time history of pore water pressure (a) and effective confining pressure (b) at point a in case P8 for the progressive wave

Full size image
Fig. 7
figure 7

Predicted stress paths indicating the PSR in case P8 for the progressive wave loading

Full size image

Figure 8 shows the predicted pore water pressure with the depth of seabed soil for all these eight cases after 25 cycles of wave loading. It should be noted that these results are recorded for the full 25 cycles, which is different from the results presented above for 19 cycles of case P8. Generally, all the results show nonlinear behaviors with the depth, especially for the cases with higher cyclic stress ratios χ 0, and the largest water pressure occurs around the mid-depth for higher cyclic stress ratios. It shows that a larger cyclic stress ratio leads to a larger pore water pressure. In the case of P8 at the depth of 15 mm, the modified model brings the soil to liquefaction in the 19th cycle, while the original model only achieves the maximum pore water pressure of 5.8 kPa in the 25th cycle, which is close but still does not reach liquefaction. In the case of P7, the modified model achieves liquefaction in the last cycle, while the original model only predicts the maximum pore water pressure of 4.6 kPa, which is lower than the modified model and does not reach liquefaction. The occurrence of liquefaction in the cases of P7 and P8 predicted by the modified model agrees well with the experimental results by Sassa and Sekiguchi [13]. In their experiments, the cyclic stress ratio χ 0 of 0.14 in the case of P7 is the critical value, above which liquefaction will occur. In the case of P6, liquefaction does not occur with both two models, but the modified model predicts a larger pore water pressure than the original model. Similarly, the modified model predicts higher pore water pressures than the original model in the cases of P3, P4, and P5. However, this difference between the original model and modified model becomes unapparent when the cyclic stress ratio becomes smaller. In the cases of P1 and P2, the results from the original model and modified model are very similar, only a slight difference around the depth of 15 mm in case P2 can be observed. It is obvious that the impact of PSR in the modified model is dependent on the cyclic stress ratio or the magnitude of wave loading. This can be explained by the stress path in Fig. 7. A larger wave loading tends to bring the normal stress closer to zero, and the magnitude of normal stress difference becomes closer to the magnitude of shear stress. This will lead to a larger change in principal stress orientation, which results in a larger impact of the modified model.

Fig. 8
figure 8

Predicted maximum pore water pressure under progressive wave loadings, a full range of depth, b above the depth of 20 mm

Full size image

Figure 9 shows the relationship between the cyclic stress ratio and the normalized pore water pressure at the depth of 15 mm, including the predictions and laboratory results. The test results indicate that a larger cyclic stress ratio leads to a larger pore water pressure. The predictions by the original and modified model reflect this trend, although the predicted pore water pressure is slightly larger than that in the laboratory results at a smaller cyclic stress ratio. The test results also indicate that the soil reaches liquefaction when the cyclic stress ratio is above 0.14, which corresponds to the case of P7. This is also called critical cyclic stress ratio [13]. While Fig. 9 indicates that the modified model can very well simulate the occurrence of liquefaction above the critical cyclic stress ratio, the original model is not capable of simulating it due to its inappropriate treatment of PSR impacts.

Fig. 9
figure 9

Comparison of normalized pore water pressure with χ 0 at the depth of 15 mm between the predicted results and laboratory results under the progressive wave loading

Full size image

4.3 Predictions under the standing waves

Figure 10 shows the relationship between the cyclic stress ratio and the normalized pore water pressure under the standing waves at the depth of 5 mm at the antinode in Fig. 4, including both the predictions and laboratory results. It should be noted that the original model and the modified model give almost the same prediction. This is because the antinode is at the centerline in the symmetrical setup under the standing wave, and the shear stress is zero at the antinode, which does not result in the PSR. Similar to the progressive wave loading, the test results in Fig. 10 indicate that the pore water pressure increases with increasing cyclic stress ratio until it reaches the critical cyclic stress ratio of 0.2, above which liquefaction occurs. The model predictions can capture this trend, and the predicted pore water pressure increases with increasing cyclic stress ratio, except the predictions are larger than the test results. On the aspect of critical cyclic stress ratio and occurrence of liquefaction, the predictions agree very well with the test results. The model also predicts that the critical cyclic stress ratio is 0.2, and liquefaction occurs above it. Figure 10 also shows the predictions at the near node, which is close to the side boundary and 85 mm to the centerline. The wave loading is not symmetrical at the near node, and there is shear stress and corresponding change in principal stress orientation. Similar to the predictions under the progressive wave, the predicted pore water pressure by using the modified model is larger than that using the original model due to the impact of PSR.

Fig. 10
figure 10

Comparison of normalized pore water pressure with χ 0 at the depth of 5 mm between the predicted results and laboratory results under the standing wave loading

Full size image

5 Conclusion

This paper simulates the wave–seabed interaction by using a newly developed PSR model which can properly consider the impact of principal stress rotations. This model is developed based on a well-established original kinematic hardening model which employs the critical state and bounding surface concept. Both the original model and modified PSR model are firstly verified in simulations of soil responses in triaxial tests and hollow cylindrical tests. Although the original model can simulate the responses in triaxial tests very well, its simulation of responses in hollow cylindrical tests is not accurate. The modified model is capable of simulating both responses due to its separate consideration of PSR impacts. The model is numerically implemented into the FEM software to study the wave–seabed interactions under both progressive waves and standing waves with various amplitudes, and the following conclusions can be drawn from the simulations.

  1. 1.

    A larger wave loading magnitude, represented by the cyclic stress ratio, leads to a larger pore water pressure in the seabed soil under both progressive and standing waves. This trend of predictions by using both models is in agreement with that in the test results.

  2. 2.

    The progressive loading can generate considerable PSR in the seabed soil, and the impact of PSR increases with increasing wave magnitudes. The PSR soil model predicts larger pore water pressure development than the original soil model. The PSR model can predict the critical cyclic stress ratio above which soil liquefaction occurs, which is in good agreement with the test results. The original soil model is not capable of bringing the soil into liquefaction.

  3. 3.

    The predictions of pore water pressure development by using both soil models are the same at the antinode under the standing wave, due to its symmetrical condition at the antinode. The predictions of critical cyclic stress ratio are in very good agreement with the test results. Away from the center symmetrical line, the modified model predicts a larger pore water pressure development than the original model.

  4. 4.

    It is evident that both the progressive wave and the standing wave loadings produce the PSR and non-coaxiality in wave–seabed interactions. As the natural wave loadings are much more random and may be the combination of these two types of waves, it is important to consider the PSR effect in offshore foundation designs. Therefore, the modified model presented in this paper has an implication and plays an important role in the simulations of wave–seabed interactions.