Skip to main content
SpringerLink
Log in

Six operations and Lefschetz-Verdier formula for Deligne-Mumford stacks

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

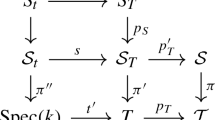
Laszlo and Olsson constructed Grothendieck’s six operations for constructible complexes on Artin stacks in étale cohomology under an assumption of finite cohomological dimension, with base change established on the level of sheaves. We give a more direct construction of the six operations for complexes on Deligne-Mumford stacks without the finiteness assumption and establish base change theorems in derived categories. One key tool in our construction is the theory of gluing finitely many pseudofunctors developed by Zheng (2014). As an application, we prove a Lefschetz-Verdier formula for Deligne-Mumford stacks. We include both torsion and ℓ-adic coefficients.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Artin M, Grothendieck A, Verdier J-L (directeurs), et al. Théorie des topos et cohomologie étale des schémas. Séminaire de Géometrie Algébrique du Bois-Marie 1963–1964 (SGA 4). Lecture Notes in Mathematics, vol. 269, 270, 305. Berlin: Springer-Verlag, 1972

    Google Scholar 

  2. Behrend K A. Derived l-adic categories for algebraic stacks. Mem Amer Math Soc, 2003, 163: 93pp

    Google Scholar 

  3. Beĭlinson A A, Bernstein J, Deligne P. Faisceaux pervers. In: Analysis and Topology on Singular Spaces, I, Astérisque, vol. 100. Paris: Soc Math France, 1982, 5–171

    Google Scholar 

  4. Conrad B. The Keel-Mori theorem via stacks. Preprint, 2005

    Google Scholar 

  5. Conrad B, Lieblich M, Olsson M. Nagata compactification for algebraic spaces. J Inst Math Jussieu, 2012, 11: 747–814

    Article  MATH  MathSciNet  Google Scholar 

  6. Deligne P. La conjecture de Weil, II. Inst Hautes études Sci Publ Math, 1980, 52: 137–252

    Article  MATH  MathSciNet  Google Scholar 

  7. Deligne P, avec la collaboration de Boutot J-F, Grothendieck A, et al. Cohomologie étale. Lecture Notes in Mathematics, vol. 569. Berlin: Springer-Verlag, 1977

    Book  MATH  Google Scholar 

  8. Ekedahl T. On the adic formalism. In: The Grothendieck Festschrift, vol. II. Progr Math, vol. 87. Boston, MA: Birkhäuser, 1990, 197–218

    Google Scholar 

  9. Gabriel P, Zisman M. Calculus of Fractions and Homotopy Theory. In: Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 35. New York: Springer-Verlag, 1967

    Google Scholar 

  10. Grothendieck A. Sur quelques points d’algèbre homologique. Tôhoku Math J, 1957, 9: 119–221

    MATH  MathSciNet  Google Scholar 

  11. Grothendieck A (directeur), avec la collaboration de Bucur I, Houzel C, et al. Cohomologie ℓ-adique et fonctions L. Séminaire de Géometrie Algébrique du Bois-Marie 1965–1966 (SGA 5). Lecture Notes in Mathematics, vol. 589. Berlin: Springer-Verlag, 1977

    Google Scholar 

  12. Illusie L, Laszlo Y, Orgogozo F (directeurs), et al. Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents. Séminaire à l’école polytechnique, 2006–2008. Paris: Astérisque, 2014, 363–364

    Google Scholar 

  13. Illusie L. Cohomological dimension: First results. In [12], Exposé XVIIIA, 455–459

    Google Scholar 

  14. Illusie L, Zheng W. Odds and ends on finite group actions and traces. Int Math Res Not, 2013, 2013: 1–62

    MATH  MathSciNet  Google Scholar 

  15. Illusie L, Zheng W. Quotient stacks and equivariant étale cohomology algebras: Quillen’s theory revisited. ArXiv:1305.0365, 2013

    Google Scholar 

  16. Kashiwara M, Schapira P. Categories and Sheaves. Grundlehren der Mathematischen Wissenschaften, vol. 332. Berlin: Springer, 2006

    MATH  Google Scholar 

  17. Keel S, Mori S. Quotients by groupoids. Ann of Math, 1997, 145: 193–213

    Article  MATH  MathSciNet  Google Scholar 

  18. Knutson D. Algebraic Spaces. Lecture Notes in Mathematics, vol. 203. Berlin: Springer-Verlag, 1971

    MATH  Google Scholar 

  19. Laszlo Y, Olsson M. The six operations for sheaves on Artin stacks, I: Finite coefficients. Publ Math Inst Hautes études Sci, 2008, 107: 109–168

    Article  MATH  MathSciNet  Google Scholar 

  20. Laszlo Y, Olsson M. The six operations for sheaves on Artin stacks, II: Adic coefficients. Publ Math Inst Hautes études Sci, 2008, 107: 169–210

    Article  MATH  MathSciNet  Google Scholar 

  21. Laumon G. Comparaison de caractéristiques d’Euler-Poincaré en cohomologie l-adique. C R Acad Sci Paris Sér I Math, 1981, 292: 209–212

    MATH  MathSciNet  Google Scholar 

  22. Laumon G, Moret-Bailly L. Champs Algébriques. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 39. Berlin: Springer-Verlag, 2000

    MATH  Google Scholar 

  23. Liu Y, Zheng W. Gluing restricted nerves of ∞-categories. ArXiv:1211.5294, 2012

    Google Scholar 

  24. Liu Y, Zheng W. Enhanced six operations and base change theorem for Artin stacks. ArXiv:1211.5948, 2012

    Google Scholar 

  25. Liu Y, Zheng W. Enhanced adic formalism and perverse t-structures for higher Artin stacks. ArXiv:1404.1128, 2014

    Google Scholar 

  26. Olsson M. Fujiwara’s theorem for equivariant correspondences. J Algebraic Geom, 2014, in press

    Google Scholar 

  27. Orgogozo F. Le théorème de finitude. In [12], Exposé XIII, 261–275

    Google Scholar 

  28. Rickard J. Derived categories and stable equivalence. J Pure Appl Algebra, 1989, 61: 303–317

    Article  MATH  MathSciNet  Google Scholar 

  29. Riou J. Dualité. In [12], Exposé XVII, 351–453

    Google Scholar 

  30. Rydh D. Compactification of tame Deligne-Mumford stacks. Preprint, 2011

    Google Scholar 

  31. Rydh D. Existence and properties of geometric quotients. J Algebraic Geom, 2013, 22: 626–669

    Article  MathSciNet  Google Scholar 

  32. Serre J-P. Représentations linéaires des groupes finis. 5th ed. Paris: Hermann, 1998

    MATH  Google Scholar 

  33. The Stacks Project Authors. Stacks Project, http://math.columbia.edu/algebraic_geometry/stacks-git

  34. Varshavsky Y. Lefschetz-Verdier trace formula and a generalization of a theorem of Fujiwara. Geom Funct Anal, 2007, 17: 271–319

    Article  MATH  MathSciNet  Google Scholar 

  35. Zheng W. Sur l’indépendance de l en cohomologie l-adique sur les corps locaux. Ann Sci éc Norm Supér, 2009, 42: 291–334

    MATH  Google Scholar 

  36. Zheng W. Gluing pseudofunctors via n-fold categories. ArXiv:1211.1877v3, 2014

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Morningside Center of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Weizhe Zheng

Authors
  1. Weizhe Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weizhe Zheng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, W. Six operations and Lefschetz-Verdier formula for Deligne-Mumford stacks. Sci. China Math. 58, 565–632 (2015). https://doi.org/10.1007/s11425-015-4970-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-015-4970-z

Keywords

MSC(2010)

Search

Navigation