A Critical Comparison of Some Metrological Parameters Characterizing Local Digital Image Correlation and Grid Method

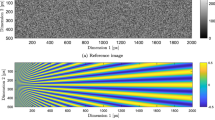
Abstract

The main metrological performance of two full-field measurement techniques, namely local digital image correlation (DIC) and grid method (GM), are compared in this paper. The fundamentals of these techniques are first briefly recalled. The formal link which exists between them is then given (the details of the calculation are in Appendix 1). Under mild assumptions, it is shown that GM theoretically gives the same result as DIC, since the formula providing the displacement with GM is the solution of the minimization of the cost function used in DIC in the particular case of a regular marking. In practice however, the way the solution is found being totally different from one technique to another, they feature different metrological performance. Some of the metrological characteristics of DIC and GM are studied in this paper. Since neither guideline nor precise standard is available to perform a fair comparison between them, a methodology must first be defined. It is proposed here to rely on three metrological parameters, namely the displacement resolution, the bias and the spatial resolution, to assess the metrological performance of each technique. These three parameters are thoroughly defined in the paper. Some of these quantities depend on external parameters such as the pattern of the surface of interest, so the same set of grid images is processed with both techniques. Only the contribution of the camera sensor noise to the displacement resolution is considered in this study. The displacement resolution, the bias and the spatial resolution are not independent but linked. These links are therefore studied in depth for DIC and GM and compared. In particular, it is shown that the product between the displacement resolution and the spatial resolution can be considered as a metric to perform this comparison. The extension to speckled patterns of the lessons drawn from grids is finally addressed in the last part of the paper. As a general conclusion, it can be said that for the value of the bias fixed in this study, the additional cost due to grid depositing offers GM to feature a better compromise than subset-based local DIC between displacement resolution and spatial resolution.

Appendices

Appendix 1: Formal Link Between DIC and GM

The aim of this calculation is to give the formal link that exists between DIC and GM. Let s ^ref and s ^cur be two images taken before and after deformation, respectively. In local DIC, estimating the 2D displacement (u _x ,u _y ) at a given point (x ₀,y ₀) consists in minimizing the squared optical residual in a neighbourhood Ω of (x ₀,y ₀), which writes:

$$ \iint_{(x,y)\in{\Omega}} (s^{ref}(x,y)-s^{cur}(x+u_{x},y+u_{y}))^{2}\;\text{d} x \;\text{d} y $$

(44)

where (x ₀,y ₀) ∈ Ω. This is a continuous version of equation (1) used with DIC. By a slight abuse of notation, we keep on denoting by s ^ref and s ^cur the restriction of both images s ^ref and s ^cur to Ω, this restriction being extended to $\mathbb {R}^{2}$ as s ^ref(x,y) = 0 and s ^cur(x,y) = 0 when (x,y) is not in Ω. Thus equation (44) writes:

$$ \iint_{(x,y)\in\mathbb{R}^{2}} (s^{ref}(x,y)-s^{cur}(x+u_{x},y+u_{y}))^{2}\;\text{d} x \;\text{d} y $$

(45)

Extending to $\mathbb {R}^{2}$ the domain of integration enables us to use the Parseval theorem (also named Plancherel theorem), which states that, under mild assumptions, any function f and its Fourier transform $\widehat {f}$ are such that ${\int }_{\mathbb {R}^{2}} |f|^{2} = K {\int }_{\mathbb {R}^{2}} |\widehat {f}|^{2}$, where K is some constant independent from f, and |z| is the norm of any complex number z. In addition, denoting s ^′cur(x,y) = s ^cur(x + u _x ,y + u _y ) and assuming that the displacement (u _x ,u _y ) is constant over Ω, we have $\widehat {s^{\prime cur}}(\xi ,\eta ) = e^{2i\pi (\xi u_{x}+\eta u_{y})} \widehat {s^{cur}}(\xi ,\eta )$. As a consequence, minimizing the squared optical residual $\iint (s^{ref} - s^{\prime cur})^{2}$ (cf. equation (45)) is equivalent to minimizing

$$ \iint_{(\xi,\eta)\in\mathbb{R}^{2}} \left|\widehat{s^{ref}}(\xi,\eta) - e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\ \right|^{2} \;\text{d} \xi \;\text{d} \eta $$

(46)

For any complex number z ₁ and z ₂, $|z_{1} - z_{2}|^{2}=|z_{1}|^{2}+|z_{2}|^{2}-2\text {Re}(z_{2}\overline {z_{1}})$ where Re(z) denotes the real part and $\overline {z}$ the complex conjugate. The quantity defined in equation (46) is thus equal to:

$$\begin{array}{@{}rcl@{}} &&\iint_{(\xi,\eta)\in\mathbb{R}^{2}} \left( |\widehat{s^{ref}}(\xi,\eta)|^{2} + |\widehat{s^{cur}}(\xi,\eta)|^{2}\right. \\&&-\left.2\text{Re}(e^{2i\pi(\xi u_{x}+\eta u_{y})}\widehat{s^{cur}}(\xi,\eta) \overline{\widehat{s^{ref}}}(\xi,\eta)) \right) \;\text{d} \xi \;\text{d} \eta \end{array} $$

(47)

The optimum translation (u _x ,u _y ) has to satisfy Euler-Lagrange equation, that is, the derivative of the integrand with respect to u _x and u _y must be null. As a consequence, for any ξ,η,

$$ \left\{ \begin{array}{l} \text{Re} \left( 2i\pi \xi e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta) \right) = 0 \\ \text{Re} \left( 2i\pi \eta e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta) \right)= 0 \end{array}\right. $$

(48)

Both equalities eventually give:

$$ \arg \left( e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta)\right) = 0 \;[\pi] $$

(49)

where arg is the argument of any non-zero complex number, the equation holding modulo π. Since we are looking for a minimum, the second derivative of the integrand must be positive, thus

$$ \left\{ \begin{array}{l} - 2 \text{Re} \left( -4\pi^{2} \xi^{2} e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta) \right) > 0 \\ -2 \text{Re} \left( -4\pi^{2} \eta^{2} e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta) \right)> 0 \end{array}\right. $$

(50)

A consequence if that equation (49) actually holds modulo 2π instead of π. Indeed, for any ξ and η, $e^{2i\pi (\xi u+\eta v)} \widehat {s^{cur}}(\xi ,\eta )\overline {\widehat {s^{ref}}}(\xi ,\eta )$ is a real number from equation (49), which must be positive from equation (50). Consequently:

$$ \arg \left( e^{2i\pi(\xi u_{x}+\eta u_{y})} \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta)\right) = 0 \;[2\pi] $$

(51)

We can conclude that, for any (ξ,η), the displacement (u _x ,u _y ) satisfies:

$$ \xi u_{x} + \eta u_{y} = - \frac{1}{2\pi} \arg \left( \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta)\right) $$

(52)

This calculation is not particular to grid images; it is valid for any pair of translated images. Retrieving u _x and u _y from equation (52) is the basis of the so-called phase correlation method [62]. Two approaches are recalled in [62] to solve this problem. With the first one, u _x and u _y can be estimated through a multivariate linear regression on the scatter plot of (ξ,η) against the values of $\arg \left (\widehat {s_{2}}(\xi ,\eta )\overline {\widehat {s^{ref}}}(\xi ,\eta )\right )/(2\pi )$ computed from the discrete Fourier transform of both images s ^ref and s ^cur. With the second method, since equation (52) is equivalent to:

$$ A e^{2i\pi(\xi u_{x} + \eta u_{y})} = \widehat{s^{cur}}(\xi,\eta)\overline{\widehat{s^{ref}}}(\xi,\eta) $$

(53)

where A > 0, the inverse Fourier transform of the right-hand member of this equality should be a Dirac distribution located at (u _x ,u _y ). As a consequence, finding (u _x ,u _y ) consists in localizing the corresponding peak. While the first approach suffers from phase wrapping and noise, the second one is not adapted to cases where u,v are below one pixel, or needs a careful interpolation to reach such low values [63].

As far as images of grids of nominal pitch p are concerned, it is possible to further simplify equation (52). The spectrum of grid images has been thoroughly studied in [41] by using the stationary phase method. It has been shown that this spectrum is made of separated spikes lying around the harmonics of the grid, the spikes being precisely expressed by Equation 9 of [41] (adapted to match the notations of the present paper). For instance, for any (ξ,η) around the fundamental harmonics $\left (\frac {1}{p},0\right )$, the following equation holds:

$$ \xi u_{x}+\eta u_{y} = - \frac{1}{2\pi} \arg \left( \widehat{e^{i{\Phi}^{cur}_{x}}}(\xi-\frac{1}{p},\eta)\overline{\widehat{e^{i{\Phi}^{ref}_{x}}}}(\xi-\frac{1}{p},\eta)\right) $$

(54)

and for any (ξ,η) around the fundamental harmonics $\left (0,\frac {1}{p}\right )$:

$$ \xi u_{x}+\eta u_{y} = - \frac{1}{2\pi} \arg \left( \widehat{e^{i{\Phi}^{cur}_{y}}}(\xi,\eta-\frac{1}{p})\overline{\widehat{e^{i{\Phi}^{ref}_{y}}}}(\xi,\eta-\frac{1}{p})\right) $$

(55)

u _x and u _y can be retrieved from these equations by using several approaches, for instance the Geometric Phase Analysis (GPA) [37], its windowed version [39], or the localized spectrum analysis [17] used in the present study.

If the phase modulations Φ _x and Φ _y can be considered as constant in Ω (that is, no phase modulation caused by grid manufacturing constraints is allowed), then $\widehat {e^{i{\Phi }}} = e^{i {\Phi }} \delta _{(0,0)}$ where δ is the Dirac distribution. In this case, equations (54)–(55) give:

$$ u_{i} = - \frac{p}{2\pi} \left( {\Phi}^{cur}_{i} - {\Phi}^{ref}_{i} \right) \quad i \in \{x,y\} $$

(56)

which is equation (11) used with GM.

As a conclusion, it can be said that under mild assumption, minimizing the optical residual on a subset requires iterative calculations in case of random pattern (DIC), but is straightforward in case of regular pattern (GM). It means that assuming that the displacement field and the phase modulations are constant within the subset, both approaches should theoretically give the same estimation. This demonstration argues that both methods should theoretically provide the same solution if the small strain assumptions holds, since in this case displacement fields are nearly constant. In practice, both methods differ because of several reasons. It is possible to mention: algorithmic considerations (how to set the stopping criteria?), practical considerations (grids are not perfectly periodic and speckles show areas where pixel intensity does not provide any information, the gradient being nul for instance), noise propagation, which differs in both methods. Since no unifying theoretical framework exists yet to compare both methods with respect to these criteria, this motivates the numerical experiments provided to the reader in the present paper.

Appendix 2: Savitzky-Golay Coefficients

In the case of DIC, for a matching function of degree d and for a subset size 2M + 1, the $h(i)=h^{DIC}_{M,d}(i)$ coefficients involved in equation (20), i = 0⋯M are defined by:

$$ h^{DIC}_{M,d}(i)=\frac{p_{i}}{norm} $$

(57)

The values for the p _i coefficients and for norm are defined in Tables 3–5 in the case d = 2.

Table 3 Savitzky-Golay coefficients, d=2, M = 3 [51]

Table 4 Savitzky-Golay coefficients, d=2, M = 6 [51]

Table 5 Savitzky-Golay coefficients, d=2, M = 10 [51]