Abstract
Generalized orthogonal linear derivative (GOLD) estimates were proposed to correct a problem of correlated estimation errors in generalized local linear approximation (GLLA). This paper shows that GOLD estimates are related to GLLA estimates by the Gram–Schmidt orthogonalization process. Analytical work suggests that GLLA estimates are derivatives of an approximating polynomial and GOLD estimates are linear combinations of these derivatives. A series of simulation studies then further investigates and tests the analytical properties derived. The first study shows that when approximating or smoothing noisy data, GLLA outperforms GOLD, but when interpolating noisy data GOLD outperforms GLLA. The second study shows that when data are not noisy, GLLA always outperforms GOLD in terms of derivative estimation. Thus, when data can be smoothed or are not noisy, GLLA is preferred whereas when they cannot then GOLD is preferred. The last studies show situations where GOLD can produce biased estimates. In spite of these possible shortcomings of GOLD to produce accurate and unbiased estimates, GOLD may still provide adequate or improved model estimation because of its orthogonal error structure. However, GOLD should not be used purely for derivative estimation because the error covariance structure is irrelevant in this case. Future research should attempt to find orthogonal polynomial derivative estimators that produce accurate and unbiased derivatives with an orthogonal error structure.


Similar content being viewed by others
Notes
Some confusion may have arisen from some of the terminology used for derivative estimation. Time-delays and embeddings sound exotic and potentially mysterious. The fact that the terms originate from the study of nonlinear and chaotic dynamics in physics (Abarbanel, 1996; Abarbanel, Brown, Sidorowich, & Tsimring, 1993) and the embedding theorems from Whitney (1936) in topological mathematics might aid in this misunderstanding. When conjoined with the practice of estimating derivatives which has roots in chemical spectroscopy Savitzky and Golay (1964), latent growth curves (McArdle & Epstein, 1987), and latent differential equations (Boker et al., 2004), it appears that some number of missteps are inevitable.
Recall that because \(\varvec{Q}\) is orthogonal \(\varvec{Q}^\mathsf{T} = \varvec{Q}^{-1} \).
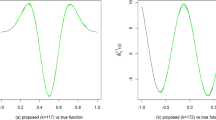
Although the error is generated with standard deviation (SD) equal to \(0.25*(SD_\mathrm{true})\), the SD of the error relative to the fitted observations is not 0.25. It is closer to 0.5. This is because the observations are polynomials. Polynomials explode at the tails and this drives the SD up. But the fitting does not occur in the tails, only at the middle of an 11-point window. So the SD of the fitted observations is much smaller than the SD of the total observations. This means the signal-to-noise ratio (of variances) for the fitted observations is about \(mean(10*\mathrm{log}10(SNRv))\,=\,4.61\,dB\), not \(10*\mathrm{log}10(16)\,=\,12.04 dB\). In other words, for the data fitted here, the error does not account for 1/17 (approximately 6%) of the total variance. Rather, it accounts for about \(\mathrm{mean}(NR2)\,=\,28.8\) % of the total variance. To say it a third time, the raw signal-to-noise ratio is not 16, but rather is closer to 4.
Note that in Table 1 the 3rd and 4th order derivative results are identical. This is necessarily true when using a fourth-order polynomial. In general, the highest two derivative orders possible for a polynomial will always be identical across GLLA and GOLD.
References
Abarbanel, H. D. I. (1996). Analysis of observed chaotic data. New York: Springer.
Abarbanel, H. D. I., Brown, R., Sidorowich, J. J., & Tsimring, L. S. (1993). The analysis of observed chaotic data in physical systems. Reviews of Modern Physics, 65(4), 1331–1392. doi:10.1103/RevModPhys.65.1331.
Bisconti, T. L., Bergeman, C. S., & Boker, S. M. (2004). Emotional well-being in recently bereaved widows: A dynamical systems approach. Journal of Gerontology, 59B, 158–167.
Bisconti, T. L., Bergeman, C. S., & Boker, S. M. (2006). Social support as a predictor of variability: An examination of the adjustment trajectories of recent widows. Psychology and Aging, 21, 590–599.
Björck, Å. (1967). Solving linear least squares problems by Gram–Schmidt othogonalization. BIT, 7, 1–21.
Boker, S. M., Deboeck, P. R., Edler, C., & Keel, P. K. (2009). Generalized local linear approximation of derivatives from time series. In S.-M. Chow, E. Ferrer, & F. Hsieh (Eds.), Statistical methods for modeling human dynamics: An interdisciplinary dialogue. Boca Raton, FL: Taylor and Francis.
Boker, S. M., & Graham, J. (1998). A dynamical systems analysis of adolescent substance abuse. Multivariate Behavioral Research, 33, 479–507. doi:10.1207/s15327906mbr3304_3.
Boker, S. M., Leibenluft, E., Deboeck, P. R., Virk, G., & Postolache, T. T. (2008). Mood oscillations and coupling between mood and weather in patients with rapid cycling bipolar disorder. International Journal of Child Health and Human Development, 1(2), 181–203.
Boker, S. M., Montpetit, M. A., Hunter, M. D., & Bergeman, C. S. (2010). Modeling resilience with diffrential equations. In P. C. M. Molenaar & K. Newell (Eds.), Individual pathways of change: Statistical models for analyzing learning and development (pp. 183–206). Washington, DC: American Psychological Association. doi:10.1037/12140-011.
Boker, S. M., Neale, M. C., & Rausch, J. (2004). Latent differential equation modeling with multivariate multi-occassion indicators. In K. van Montfort, H. Oud, & A. Satorra (Eds.), Recent developments on structural equation models: Theory and applications (pp. 151–174). Dordrecht: Kluwer Academic Publishers. doi:10.1007/978-1-4020-1958-6_9.
Boker, S. M., & Nesselroade, J. R. (2002). A method for modeling the intrinsic dynamics of intraindividual variability: Recovering the parameters of simulated oscillators in multi-wave panel data. Multivariate Behavioral Research, 37, 127–160.
Casdagli, M., Eubank, S., Farmer, J. D., & Gibson, J. (1991). State space reconstruction in the presence of noise. Physica D, 51, 52–98. doi:10.1016/0167-2789(91)90222-U.
Chow, S., Ram, N., Boker, S. M., Fujita, F., & Clore, G. (2005). Emotion as a thermostat: Representing emotion regulation using a damped oscillator model. Emotion, 5, 208–225.
Deboeck, P. R. (2010). Estimating dynamical systems: Derivative estimation hints from Sir Ronald A Fisher. Multivariate Behavioral Research, 45, 725–745. doi:10.1080/00273171.2010.498294.
Estabrook, R. (2015). Evaluating measurement of dynamic constructs: Defining a measurement model of derivatives. Psychological Methods, 20(1), 117–141. doi:10.1037/a0034523.
Fisher, R. A. (1925). The influence of rainfall on the yield of wheat at Rothamsted. Philosophical Transactions of the Royal Society of London, Series B, Containing Papers of a Biological Character, 213, 89–142.
Giona, M., Lentini, F., & Cimagalli, V. (1991). Functional reconstruction and local prediction of chaotic time series. Physical Review A, 44(6), 3496. doi:10.1103/PhysRevA.44.3496.
Hamaker, E. L., Nesselroade, J. R., & Molenaar, P. C. M. (2007). The integrated trait-state model. Journal of Research in Personality, 41, 295–315. doi:10.1016/j.jrp.2006.04.003.
Landau, R. H., Páez, M. J., & Bordeianu, C. C. (2007). Computational physics: Problem solving with computers (2nd ed.). Weinheim: Wiley-VCH.
Lay, D. C. (2003). Linear algebra and its applications (3rd ed.). Boston, MA: Addison Wesley.
Leon, S. J. (2006). Linear algebra with applications (7th ed.). Upper Saddle River, NJ: Prentice Hall.
McArdle, J. J., & Epstein, D. (1987). Latent growth curves within developmental structural equation models. Child Development, 58, 110–133.
Molenaar, P. C. M., & Newell, K. M. (2003). Direct fit of theoretical model of phase transition in oscillatory finger motions. British Journal of Mathematical and Statistical Psychology, 56, 199–214. doi:10.1348/000711003770480002.
Narula, S. C. (1979). Orthogonal polynomial regression. International Statistical Review, 47(1), 31–36.
Oud, J. H. L., & Folmer, H. (2011). Reply to Steele & Ferrer: Modeling oscillation, approximately or exactly? Multivariate Behavioral Research, 46(6), 985–993. doi:10.1080/00273171.2011.625306.
Savitzky, A., & Golay, M. J. E. (1964). Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry, 36(9), 1627–1639.
Song, H., & Ferrer, E. (2009). State-space modeling of dynamic psychological processes via the Kalman smoother algorithm: Rationale, finite sample properties, and applications. Structural Equation Modeling, 16, 338–363. doi:10.1080/10705510902751432.
Steele, J. S., & Ferrer, E. (2011). Latent differential equation modeling of self-regulatory and coregulatory affective processes. Multivariate Behavioral Research, 46(6), 956–984. doi:10.1080/00273171.2011.625305.
Trail, J. B., Collins, L. M., Rivera, D. E., Li, R., Piper, M. E., & Baker, T. B. (2014). unctional data analysis for dynamical system identification of behavioral processes. Psychological Methods, 19, 175–187. doi:10.1037/a0034035.
Whitney, H. (1936). Differentiable manifolds. The Annals of Mathematics, 37(3), 645–680. Retrieved from http://www.jstor.org/stable/1968482.
Whittaker, E. T., & Robinson, G. (1924). The calculus of observations: A treatise on numerical mathematics (vol. 36) (No. 9). London.
Yang, M., & Chow, S. (2010). Using state-space model with regime switching to represent the dynamics of facial electromyography (EMG) data. Psychometrika, 75, 744–771. doi:10.1007/s11336-010-9176-2.
Zentall, S. R., Boker, S. M., & Braungart-Rieker, J. M. (2006, June). Mother-infant synchrony: A dynamical systems approach. In Proceedings of the Fifth International Conference on Development and Learning.
Zheng, Y., Wiebe, R. P., Cleveland, H. H., Molenaar, P. C., & Harris, K. S. (2013). An idiographic examination of day-to-day patterns of substance use craving, negative affect, and tobacco use among young adults in recovery. Multivariate Behavioral Research, 48(2), 241–266. doi:10.1080/00273171.2013.763012.
Acknowledgments
The author is grateful to Joseph L. Rodgers for helpful comments on earlier drafts of this article, and to the reviewers and associate editor for their invaluable feedback.
Author information
Authors and Affiliations
Corresponding author
Appendix: Mathematical Background and a Lemma
Appendix: Mathematical Background and a Lemma
1.1 Background
Three items of sometimes unfamiliar mathematics will be vitally important: the dot product, vector projection, and the Gram–Schmidt orthogonalization process. For vectors \(\varvec{x} = \left( x_1 ,~ x_2 ,~ x_3 ,\ldots , x_n \right) ^\mathsf{T}\) and \(\varvec{y} = \left( y_1 ,~ y_2 ,~ y_3 , \ldots , y_n \right) ^\mathsf{T}\), the dot product, or scalar product, of the two vectors is written
The projection of \(\varvec{x}\) in the direction of \(\varvec{y}\) is defined as
It can be derived without much difficulty, but the idea of vector projection is most easily shown graphically as in Figure 3.
In many situations, it can be useful to have an orthogonal set of vectors spanning a space of interest. The Gram–Schmidt orthogonalization process begins with an arbitrary set of basis vectors and produces an orthogonal set of basis vectors spanning the same space. Gram–Schmidt orthogonalization can be used to solve least squares problems (Björck 1967) and is often covered in introductory linear algebra course books (e.g., Lay, 2003; Leon, 2006).
If \(\varvec{u}_1, \varvec{u}_2, \varvec{u}_3, \ldots , \varvec{u}_m\) are the original basis vectors, then \(\varvec{u'}_1, \varvec{u'}_2, \varvec{u'}_3, \ldots , \varvec{u'}_m\) are the new orthogonal basis vectors defined by
So the \(k^{th}\) new basis vector,
Figure 4 illustrates a two-dimensional example of the Gram–Schmidt orthogonalization process. When beginning with a nonorthogonal set of basis vectors \(\{\varvec{u_1}, \varvec{u_2}\}\) that spans the two-dimensional space, then the Gram–Schmidt procedure produces a new set of orthogonal basis vectors \(\{\varvec{u'_1}, \varvec{u'_2}\}\) that spans the same space.
1.2 Lemma Regarding Orthogonal Vectors and Projections
Let \(\varvec{u}_1, \ldots , \varvec{u}_m\) be any full rank set of m vectors, and let \(\varvec{u'}_1, \ldots , \varvec{u'}_m\) be the set of orthogonalized vectors produced by applying the Gram–Schmidt orthogonalization process to \(\varvec{u}_1, \ldots , \varvec{u}_m\). We want to show that for any \(k \in \{ 1, 2, 3, \ldots , m \}, ~~ \varvec{u'}_k \bullet \varvec{u'}_k = \varvec{u'}_k \bullet \varvec{u}_k\). By substitution based on the Gram–Schmidt definition and that of vector projection
And because the dot product follows a distributive law
Again, applying the distributive law and expanding the summation,
Now rearranging terms
The underbraced terms are all zero because we know that the new Gram–Schmidt basis vectors, \(\varvec{u'}_i\), are orthogonal. So finally,
We have thus shown that \(\varvec{u'}_k \bullet \varvec{u'}_k = \varvec{u'}_k \bullet \varvec{u}_k\), and the proof is complete.
\(\square \)
Rights and permissions
About this article
Cite this article
Hunter, M.D. As Good as GOLD: Gram–Schmidt Orthogonalization by Another Name. Psychometrika 81, 969–991 (2016). https://doi.org/10.1007/s11336-016-9511-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11336-016-9511-3