Power allocation and effective capacity of AF successive relays

Abstract

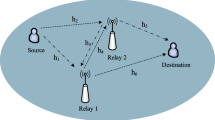
In the relay based telecommunications with K relays between the source and destination, $K+1$ time or frequency slots are required for a single frame transmission. However, without the relays, only one time or frequency slot is used for a single frame transmission. Therefore, despite the benefits of relaying systems, this type of communications is not efficient from the spectral efficiency viewpoint. One solution to reduce this issue might be the full-duplex (FD) relays. An old technique which is reconsidered recently to improve the spectral efficiency of telecommunication systems. However, FD relays have a certain complexity, so, some similar techniques such as successive relays with nearly the same performance but less complexity is taken into account now. In successive relaying systems, two relays between the source and destination are employed which receive the transmitted frames from the source and relay it to the destination successively. This structure generally acts like an FD relays. In this paper, the effective capacity performance of an amplify and forward successive relaying systems with power allocation strategy at the relays are studied perfectly. However, while the inter-rely interference (IRI) between two successive relays has to be managed well, the power allocation and the effective capacity is derived under different assumptions about the IRI. In this way, we assume weak or strong, short or long-term constraints on the IRI. Then we extract the optimal transmitted power at the relay to maximize the effective capacity under these constraints.

Appendices

Appendix 1: Proof of (16)

First, we can write the optimization problem in a standard form as

$$\begin{aligned}&\max \nolimits _{\mu _0}-{\textsf {E}}\left\{ \left( 1+\mu _0 \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }}\right\} \nonumber \\&{\mathrm {s.t.}}\quad \quad {\textsf {E}}\left\{ \mu _0\right\} \le 1,\quad \quad {\textsf {E}}\left\{ \mu _0\gamma _{\mathrm {IR}}\right\} \le q_0\nonumber \\&-\mu _0\le 0. \end{aligned}$$

(24)

Then, using Lagrangian method, the cost function is written as

$$J=-{\textsf {E}}\left\{ \left( 1+\mu _0 \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }}\right\} +\lambda _1\left( 1-{\textsf {E}}\left\{ \mu _0\right\} \right) +\lambda _2\left( q_0-{\textsf {E}}\left\{ \mu _0\gamma _{\mathrm {IR}}\right\} \right) +\lambda _3\mu _0$$

(25)

where $\lambda _1\ge 0$, $\lambda _2\ge 0$ and $\lambda _3\ge 0$ are the nonnegative Lagrange multipliers corresponding to our constraints. Taking the partials with respect to $\mu _0$, we will have [40]

$$\begin{aligned} \frac{\partial J}{\partial \mu }&= {\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0 \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} -\lambda _1-\lambda _2{\textsf {E}}\left\{ \gamma _{\mathrm {IR}}\right\} +\lambda _3\nonumber \\&= {\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0 \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} -\lambda _1-\lambda _2\bar{\gamma }+\lambda _3. \end{aligned}$$

(26)

Now, we can find $\mu _0^{\mathrm {opt}}$, $\lambda _1^{\mathrm {opt}}$, $\lambda _2^{\mathrm {opt}}$ and $\lambda _3^{\mathrm {opt}}$ such that

$${\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} -\lambda _1^{\mathrm {opt}}-\lambda _2^{\mathrm {opt}}\bar{\gamma }+\lambda _3^{\mathrm {opt}}=0$$

(27)

and

$$\begin{aligned}&\lambda _1^{\mathrm {opt}}\left( 1-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \right) =0 \end{aligned}$$

(28)

$$\begin{aligned}&\lambda _2^{\mathrm {opt}}\left( q_0-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} \right) =0 \end{aligned}$$

(29)

and

$$\begin{aligned} \lambda _3^{\mathrm {opt}}\mu _0^{\mathrm {opt}}=0 \end{aligned}$$

(30)

correspondingly. From (30), since $\mu _0^{\mathrm {opt}}=0$ is not acceptable, we can conclude that $\lambda _3^{\mathrm {opt}}=0$. Consider (28) and (29), we can break the analysis into four different cases as follows.

• 1. If $\lambda _1^{\mathrm {opt}}=0 \left( 1-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \ne 0\right)$ and $\lambda _2^{\mathrm {opt}}=0 \left( q_0-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} \ne 0\right)$, then (27) converts to ${\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} =0$. Since we assume $\tilde{\theta }>0$, $\mu _0^{\mathrm {opt}}>0$, $\gamma _{\mathrm {eq}}>0$ and $\gamma _{\mathrm {IR}}>0$, this case is not a feasible solution.

• 2. If $\lambda _1^{\mathrm {opt}}=0\left( 1-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \ne 0\right)$ and $q_0-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} =0 (\lambda _2^{\mathrm {opt}}\ne 0)$, then (27) converts to ${\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} =\lambda _2^{\mathrm {opt}}\bar{\gamma }$. Here, we can assume $\tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}=\lambda _2^{\mathrm {opt}}\bar{\gamma }$ and $\mu _0^{\mathrm {opt}}>0$ which leads to

  $$\begin{aligned} \mu _0^{\mathrm {opt}}= {\left\{ \begin{array}{ll} 0,&{} \gamma _{\mathrm {eq}}<\frac{\lambda _2^{\mathrm {opt}}\bar{\gamma }}{\tilde{\theta }}\\ \left( \frac{\tilde{\theta }}{\lambda _2^{\mathrm {opt}}\bar{\gamma }}\right) ^\frac{1}{\tilde{\theta }+1}\left( \frac{1}{\gamma _{\mathrm {eq}}}\right) ^\frac{\tilde{\theta }}{\tilde{\theta }+1}-\frac{1}{\gamma _{\mathrm {eq}}},&{} \gamma _{\mathrm {eq}}\ge \frac{\lambda _2^{\mathrm {opt}}\bar{\gamma }}{\tilde{\theta }} \end{array}\right. }. \end{aligned}$$

  (31)

  Note that, $\lambda _2^{\mathrm {opt}}$ can be calculated from ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} ={\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \bar{\gamma }=q_0$ or equivalently ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} =q_0/\bar{\gamma }$. Since we assumed $\lambda _1^{\mathrm {opt}}=0$, then we have ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} <1$. Therefore, this case is valid when $q_0/\bar{\gamma }<1$.

• 3. If $\lambda _2^{\mathrm {opt}}=0\left( q_0-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} \ne 0\right)$ and $1-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} =0(\lambda _1^{\mathrm {opt}}\ne 0)$, then (27) converts to ${\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} =\lambda _1^{\mathrm {opt}}$. Here, we can assume $\tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}=\lambda _1^{\mathrm {opt}}$ and $\mu _0^{\mathrm {opt}}>0$ which leads to

  $$\begin{aligned} \mu _0^{\mathrm {opt}}= {\left\{ \begin{array}{ll} 0,&{} \gamma _{\mathrm {eq}}<\frac{\lambda _1^{\mathrm {opt}}}{\tilde{\theta }}\\ \left( \frac{\tilde{\theta }}{\lambda _1^{\mathrm {opt}}}\right) ^\frac{1}{\tilde{\theta }+1}\left( \frac{1}{\gamma _{\mathrm {eq}}}\right) ^\frac{\tilde{\theta }}{\tilde{\theta }+1}-\frac{1}{\gamma _{\mathrm {eq}}},&{} \gamma _{\mathrm {eq}}\ge \frac{\lambda _1^{\mathrm {opt}}}{\tilde{\theta }} \end{array}\right. }. \end{aligned}$$

  (32)

  Note that, $\lambda _1^{\mathrm {opt}}$ can be calculated from ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} =1$. Since we assumed $\lambda _2^{\mathrm {opt}}=0$, then we have ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} ={\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \bar{\gamma }<q_0$. Therefore, this case is valid when $q_0/\bar{\gamma }>1$.

• 4. If $1-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} =0(\lambda _1^{\mathrm {opt}}\ne 0)$ and $q_0-{\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} =0(\lambda _2^{\mathrm {opt}}\ne 0)$, then (27) converts to ${\textsf {E}}\left\{ \tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}\right\} =\lambda _1^{\mathrm {opt}}+\lambda _2^{\mathrm {opt}}\bar{\gamma }$. Here, we can assume $\tilde{\theta }\gamma _{\mathrm {eq}}\left( 1+\mu _0^{\mathrm {opt}} \gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }-1}=\lambda _1^{\mathrm {opt}}+\lambda _2^{\mathrm {opt}}\bar{\gamma }=\ell$ and $\mu _0^{\mathrm {opt}}>0$ which leads to

  $$\begin{aligned} \mu _0^{\mathrm {opt}}= {\left\{ \begin{array}{ll} 0,&{} \gamma _{\mathrm {eq}}<\frac{\ell }{\tilde{\theta }}\\ \left( \frac{\tilde{\theta }}{\ell }\right) ^\frac{1}{\tilde{\theta }+1}\left( \frac{1}{\gamma _{\mathrm {eq}}}\right) ^\frac{\tilde{\theta }}{\tilde{\theta }+1}-\frac{1}{\gamma _{\mathrm {eq}}},&{} \gamma _{\mathrm {eq}}\ge \frac{\ell }{\tilde{\theta }} \end{array}\right. }. \end{aligned}$$

  (33)

  Note that, $\ell$ can be calculated from both ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} =1$ or ${\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\gamma _{\mathrm {IR}}\right\} ={\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} \bar{\gamma }=q_0$ with the same value. Therefore, this case is valid when $q_0/\bar{\gamma }=1$.

Now, we can aggregate cases 2, 3 and 4 in one case such as

$$\begin{aligned} \mu _0^{\mathrm {opt}}= {\left\{ \begin{array}{ll} 0,&{} \gamma _{\mathrm {eq}}<\gamma _{{\text {T}}}\\ \left( \frac{1}{\gamma _{{\text {T}}}}\right) ^\frac{1}{\tilde{\theta }+1}\left( \frac{1}{\gamma _{\mathrm {eq}}}\right) ^\frac{\tilde{\theta }}{\tilde{\theta }+1}-\frac{1}{\gamma _{\mathrm {eq}}},&{} \gamma _{\mathrm {eq}}\ge \gamma _{{\text {T}}} \end{array}\right. }. \end{aligned}$$

(34)

where $\gamma _{{\text {T}}}$ is a cut-off SNR threshold which is determined from

$$\begin{aligned} {\textsf {E}}\left\{ \mu _0^{\mathrm {opt}}\right\} = {\left\{ \begin{array}{ll} \frac{q_0}{\bar{\gamma }},&{} q_0<\bar{\gamma }\\ 1,&{} q_0\ge \bar{\gamma } \end{array}\right. }. \end{aligned}$$

(35)

Appendix 2: Proof of (19)

By substituting (16) or (18) into (15), we will have

$$\begin{aligned} {\textsf {E}}\left\{ \left( 1+\mu _0^{\mathrm {opt}}\gamma _{\mathrm {eq}}\right) ^{-\tilde{\theta }}\right\} =\underbrace{\int _{0}^{\gamma _{{\text {T}}}}f_{\gamma _{\mathrm {eq}}}(x)dx}_{I_1}+\underbrace{\int _{\gamma _{{\text {T}}}}^{\infty }\left( x/\gamma _{{\text {T}}}\right) ^{-\tilde{\theta }/(1+\tilde{\theta })}f_{\gamma _{\mathrm {eq}}}(x)dx}_{I_2} \end{aligned}$$

(36)

where $f_{\gamma _{\mathrm {eq}}}(x)$ is presented in (2). For solving $I_1$, it can be changed to two infinite integrals as

$$\begin{aligned} I_1 &= \underbrace{\int _{0}^{\infty }f_{\gamma _{\mathrm {eq}}}(x)dx}_{I_3}-\underbrace{\int _{\gamma _{{\text {T}}}}^{\infty }f_{\gamma _{\mathrm {eq}}}(x)dx}_{I_4}\nonumber \\ &= \frac{\sqrt{\pi }}{2\Gamma (5/2)}\left[ F(3,3/2,5/2;0)+\frac{1}{2}F(2,1/2,5/2;0)\right] \nonumber \\&-\frac{\sqrt{\pi }\gamma _{{\text {T}}}}{\bar{\gamma }}\left[ G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,3/2\\ -1,2,0\end{array} \right. \right) + G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,3/2\\ -1,1,1\end{array} \right. \right) \right] \end{aligned}$$

(37)

where the closed-form solution of $I_3$ and $I_4$ is possible using [37, eq. 6.621-3] and [37, eq. 6.625-7], respectively. Once again [37, eq. 6.625-7] can be used for finding $I_2$. Therefore, we have

$$\begin{aligned} I_2 &= \frac{\sqrt{\pi }}{4}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\right) ^{\frac{1+2\tilde{\theta }}{1+\tilde{\theta }}}\left[ G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,\frac{1}{2}+\frac{1}{1+\tilde{\theta }}\\ -1,1+\frac{1}{1+\tilde{\theta }},-1+\frac{1}{1+\tilde{\theta }}\end{array} \right. \right) \right. \nonumber \\+ & {} \left. G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,\frac{1}{2}+\frac{1}{1+\tilde{\theta }}\\ -1,\frac{1}{1+\tilde{\theta }},\frac{1}{1+\tilde{\theta }}\end{array} \right. \right) \right] \end{aligned}$$

(38)

where F(., .; .; .) represents Gauss hypergeometric function [37, eq. 9.10], $\Gamma (.)$ denotes the Gamma function and $G_{p,q}^{m,n}(.)$ is the Meijer’s G function defined in [37, eq. 9.301]. Now, connecting the obtained results for $I_1$ and $I_2$, we have

$$\begin{aligned} E_C(\theta ) &= -\frac{1}{\theta }\ln \left\{ \frac{\sqrt{\pi }}{2\Gamma (5/2)}\left[ F(3,3/2,5/2;0)+\frac{1}{2}F(2,1/2,5/2;0)\right] \right. \nonumber \\- & {} \frac{\sqrt{\pi }\gamma _{{\text {T}}}}{\bar{\gamma }}\left[ G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,3/2\\ -1,2,0\end{array} \right. \right) + G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,3/2\\ -1,1,1\end{array} \right. \right) \right] \nonumber \\+ & {} \left. \frac{\sqrt{\pi }}{4}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\right) ^{\frac{1+2\tilde{\theta }}{1+\tilde{\theta }}}\left[ G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,\frac{1}{2}+\frac{1}{1+\tilde{\theta }}\\ -1,1+\frac{1}{1+\tilde{\theta }},-1+\frac{1}{1+\tilde{\theta }}\end{array} \right. \right) \right. \right. \nonumber \\+ & {} \left. \left. G_{23}^{30}\left( \frac{4\gamma _{{\text {T}}}}{\bar{\gamma }}\left| \begin{array}{l}0,\frac{1}{2}+\frac{1}{1+\tilde{\theta }}\\ -1,\frac{1}{1+\tilde{\theta }},\frac{1}{1+\tilde{\theta }}\end{array} \right. \right) \right] \right\} . \end{aligned}$$

(39)