Automatic Line Extraction in Uncalibrated Omnidirectional Cameras with Revolution Symmetry

Abstract

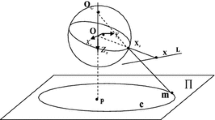
Revolution symmetry is a realistic assumption for modelling the majority of catadioptric and dioptric cameras. In central systems it can be described by a projection model based on radially symmetric distortion. In these systems straight lines are projected on curves called line-images. These curves have in general more than two degrees of freedom and their shape strongly depends on the particular camera configuration. Therefore, the existing line-extraction methods for this kind of omnidirectional cameras require the camera calibration by contrast with the perspective case where the calibration is not involved in the shape of the projected line-image. However, this drawback can be considered as an advantage because the shape of the line-images can be used for self-calibration. In this paper, we present a novel method to extract line-images in uncalibrated omnidirectional images which is valid for radially symmetric central systems. In this method we propose using the plumb-line constraint to find closed form solutions for different types of camera systems, dioptric or catadioptric. The inputs of the proposed method are points belonging to the line-images and their intensity gradient. The gradient information allows to reduce the number of points needed in the minimal solution improving the result and the robustness of the estimation. The scheme is used in a line-image extraction algorithm to obtain lines from uncalibrated omnidirectional images without any assumption about the scene. The algorithm is evaluated with synthetic and real images showing good performance. The results of this work have been implemented in an open source Matlab toolbox for evaluation and research purposes.

Appendices

Appendix 1: Polynomials Describing Line-Images

Some of the line-images in central systems with revolution symmetry can be expressed as polynomials. In this Appendix we show the description of these line images using polynomials for Catadioptric systems, Stereographic-Fisheye, Orthogonal-Fisheye and Equisolid-Fisheye systems.

Catadioptric and Stereographic-Fisheye

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\hat{x}}^2&{\hat{x}} {\hat{y}}&{\hat{y}}^2&{\hat{x}}&{\hat{y}}&1 \end{array}\right) {\varvec{\varOmega }}_{cata}=0 \end{aligned}$$

(34)

where

$$\begin{aligned} {\varvec{\varOmega }}_{cata} = \left( \begin{array}{c} n_x^2 \sin \chi ^2 - n_z^2 \cos \chi ^2 \\ 2 n_x n_y \sin \chi ^2\\ n_y^2 \sin \chi ^2 - n_z^2 \cos \chi ^2 \\ 2 f \sin \chi n_x n_z \\ 2 f \sin \chi n_y n_z \\ f^2 \sin \chi ^2 n_z^2 \\ \end{array}\right) \end{aligned}$$

(35)

Ortogonal-Fisheye

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\hat{x}}^2&{\hat{x}} {\hat{y}}&{\hat{y}}^2&{\hat{x}}&{\hat{y}}&1 \end{array}\right) {\varvec{\varOmega }}_{ortho}=0 \end{aligned}$$

(36)

where

$$\begin{aligned} {\varvec{\varOmega }}_{ortho} = \left( \begin{array}{c} -n_x^2 - n_z^2 \\ -2 n_x n_y \\ -n_y^2 - n_z^2 \\ 0 \\ 0 \\ f^2 n_z^2 \\ \end{array}\right) \end{aligned}$$

(37)

Equisolid-Fisheye

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\hat{x}}^4&{\hat{x}}^3 {\hat{y}}&{\hat{x}}^2 {\hat{y}}^2&{\hat{x}}^2&{\hat{x}} {\hat{y}}^3&{\hat{x}} {\hat{y}}&{\hat{y}}^4&{\hat{y}}^2&1 \end{array}\right) {\mathbf {Q}}=0 \end{aligned}$$

(38)

where

$$\begin{aligned} {\mathbf {Q}}=\left( \begin{array}{c} - 4 \left( n_x^2 + n_z^2 \right) \\ -8 n_x n_y \\ - 4 n_x^2 - 4 n_y^2 - 8 n_z^2 \\ 4 f^2 \left( n_x^2 + n_z^2\right) \\ -8 n_x n_y \\ 8 f^2 n_x n_y \\ - 4 \left( n_y^2 + n_z^2 \right) \\ 4 f^2 \left( n_y^2 + n_z^2 \right) \\ -f^4 n_z^2\\ \end{array}\right) \end{aligned}$$

(39)

Appendix 2: Computing the Focal Distance in Hypercatadioptric Systems

In this Appendix we expand a way for computing the focal length in hypercatadioptic systems. This allows us to compute both calibration parameters. Instead of using the plumb-line constraint or a combination between plum-line and gradient constraints the normal ${\mathbf {n}}$ can be computed from a pair of points using the gradient constraint (23).

$$\begin{aligned} \left( {\begin{array}{c@{\quad }c@{\quad }c} {-\nabla I_{y1}}&{}{\pm \nabla I_{x1}}&{}{\frac{{\partial {\hat{\alpha }} _1 }}{{\partial {\hat{r}}}}\frac{1}{{\hat{r}}_1} \left( {\hat{x}}_1\nabla I_{y1} - {\hat{y}}_1\nabla I_{x1} \right) } \\ {-\nabla I_{y2}}&{}{\pm \nabla I_{x2}}&{}{\frac{{\partial {\hat{\alpha }} _2 }}{{\partial {\hat{r}}}}\frac{1}{{\hat{r}}_2} \left( {\hat{x}}_2\nabla I_{y2} - {\hat{y}}_2\nabla I_{x2} \right) } \\ \end{array}} \right) {\mathbf {n}}=\left( {\begin{array}{c} 0 \\ 0 \\ \end{array}} \right) \end{aligned}$$

(40)

In practice, the solution is noisy and does not imply a real advantage with respect to the two point’s location approach (11).

The previous constraint (40) using two points and their gradients is enough to define a line-image. Therefore, when adding a third point with (23) in (40) one of the equations can be expressed in combination of the other two. In practice this means that,

$$\begin{aligned} \varpi _1 \frac{{\partial {\hat{\alpha }} _1 }}{{\partial {\hat{r}}}}\frac{1}{{{\hat{r}}_1 }} + \varpi _2 \frac{{\partial {\hat{\alpha }} _2 }}{{\partial {\hat{r}}}}\frac{1}{{{\hat{r}}_2 }} + \varpi _3 \frac{{\partial {\hat{\alpha }} _3 }}{{\partial {\hat{r}}}}\frac{1}{{{\hat{r}}_3 }} = 0 \end{aligned}$$

(41)

where

$$\begin{aligned} \varpi _1&= \left( {\nabla I_{x2}\nabla I_{y3}-\nabla I_{x3} \nabla I_{y2}}\right) \left( {\hat{x}}_1\nabla I_{y1}-{\hat{y}}_1\nabla I_{x1}\right) \end{aligned}$$

(42)

$$\begin{aligned} \varpi _2&= \left( {\nabla I_{x3}\nabla I_{y1}-\nabla I_{x1} \nabla I_{y3}}\right) \left( {\hat{x}}_2\nabla I_{y2}-{\hat{y}}_2\nabla I_{x2}\right) \end{aligned}$$

(43)

$$\begin{aligned} \varpi _3&= \left( {\nabla I_{x1}\nabla I_{y2}-\nabla I_{x2} \nabla I_{y1}}\right) \left( {\hat{x}}_3\nabla I_{y3}-{\hat{y}}_3\nabla I_{x3}\right) \end{aligned}$$

(44)

This constraint is similar to (13) but using gradients (notice that location information is also used).

As noted before, gradient information is noisier than location information, therefore there is no advantage in using this constraint instead of (13). However, there is a case in which this constraint is useful. The constraint (13) is solved for each system in Table 3. Most of the devices taken into account have a single calibration parameter defining distortion. This is the case of equiangular, stereographic, orthogonal and equisolid. The parabolic case is defined by two parameters $f$ and $p$ but a coupled parameter $\hat{r}_{vl} = fp$ can be used instead. In these cases the constraint involving three points can be used to estimate the calibration of the system. However, in the hyperbolic case the two parameters $\chi$ and $f$ can not be coupled and only one of them can be estimated from this constraint.

By contrast, when simplifying (41) for hypercatadioptric systems we found that mirror parameter $\chi$ is not involved:

$$\begin{aligned} \varpi _1 \frac{1}{{\sqrt{{\hat{r}}_1 ^2 + f^2 } }} + \varpi _2 \frac{1}{{\sqrt{{\hat{r}}_2 ^2 + f^2 } }} + \varpi _3 \frac{1}{{\sqrt{{\hat{r}}_3 ^2 + f^2 } }} = 0 \end{aligned}$$

(45)

As consequence, the focal distance $f$ can be computed from the gradient orientation and the location of three points lying on a line-image.

Equation (45) can be expressed as a polynomial of degree 8 (but bi-quartic),

$$\begin{aligned} \sum \limits _{m = 0}^4 \beta _m f^{2m} = 0 \end{aligned}$$

(46)

where $\beta _m = \beta _{m,123} + \beta _{m,213} + \beta _{m,312}$ and

$$\begin{aligned} \beta _{0,ijk}&= - \varpi _i^4 {\hat{r}}_j^4 {\hat{r}}_k^4 + 2 {\hat{r}}_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 \varpi _j^2 \varpi _k^2\end{aligned}$$

(47)

$$\begin{aligned} \beta _{1,ijk}&= 2\left( 2 {\hat{r}}_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 + {\hat{r}}_i^4 \left( \varpi _j^2 + \varpi _k^2 \right) \right) \varpi _j^2 \varpi _k^2 +\ldots \nonumber \\&-\,2 \varpi _i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_j^2+{\hat{r}}_k^2 \right) \end{aligned}$$

(48)

$$\begin{aligned} \beta _{2,ijk}&= {\hat{r}}_j^2 {\hat{r}}_k^2 \left( 4 \varpi ^2 \left( \varpi _j^2 + \varpi _k^2 - \varpi _i^2 \right) + 2 \varpi _j^2 \varpi _k^2 \right) \ldots \nonumber \\&-\,{\hat{r}}_i^4 \left( \varpi _j^2-\varpi _k^2 \right) ^2\end{aligned}$$

(49)

$$\begin{aligned} \beta _{3,ijk}&= {\hat{r}}_i^2 \left( \varpi _i^2 \left( \varpi _j^2+\varpi _k^2 \right) + 2 \varpi _j^2 \varpi _k^2 - \left( \varpi _j^4 + \varpi _k^4 \right) \right) \nonumber \\ \end{aligned}$$

(50)

$$\begin{aligned} \beta _{4,ijk}&= - \varpi _i^4 + 2 \varpi _j^2 \varpi _k^2 \end{aligned}$$

(51)

This equation has four solutions (because the negative values for f have not sense).

Appendix 3: Coefficients for the Equisolid-Fisheye Plumb-Line Equation

In this Appendix we present the coefficient of the 16th degree polynomial to solve the equisolid plumb-line equation (19).

$$\begin{aligned} \sum \limits _{m = 0}^8 \omega _m {\hat{r}}_{vl}^{2m} = 0 \end{aligned}$$

(52)

where $\omega _m = \omega _{m,123} + \omega _{m,213} + \omega _{m,312}$ and

$$\begin{aligned} \omega _{0,ijk}&= -l_i^4 {\hat{r}}_i^8 {\hat{r}}_j^4 {\hat{r}}_k^4 + 2 {\hat{r}}_i^4 l_j^2 l_k^2 {\hat{r}}_j^6 {\hat{r}}_k^6\end{aligned}$$

(53)

$$\begin{aligned} \omega _{1,ijk}&= 4 \left( {\hat{r}}_i^2 \left( {\hat{r}}_j^2 + {\hat{r}}_k^2 \right) + {\hat{r}}_j^2 {\hat{r}}_k^2 \right) \left( l_i^4 {\hat{r}}_i^6 {\hat{r}}_k^2 -2 l_j^2 l_k^2 {\hat{r}}_i^2 {\hat{r}}_j^4 {\hat{r}}_k^4 \right) \end{aligned}$$

(54)

$$\begin{aligned} \omega _{2,ijk}&= -16 l_i^4 {\hat{r}}_i^4 \left( {\hat{r}}_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_j^2 +{\hat{r}}_k^2 \right) + {\hat{r}}_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 \right) +\ldots \nonumber \\&+\, 32 l_j^2 l_k^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_j^2 +{\hat{r}}_k^2 \right) + {\hat{r}}_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 \right) +\ldots \nonumber \\&- \, 2 l_i^4 {\hat{r}}_i^4 \left( 2 {\hat{r}}_i^4 \left( {\hat{r}}_j^4 + {\hat{r}}_k^4 \right) + 3 {\hat{r}}_j^4 {\hat{r}}_k^4 \right) +\ldots \nonumber \\&+\, 10 l_j^2 l_k^2 {\hat{r}}_j^2 {\hat{r}}_k^2 {\hat{r}}_i^2 \left( {\hat{r}}_j^4 + {\hat{r}}_k^4 \right) \nonumber \\&+\,\ldots 8 l_j^2 l_k^2 {\hat{r}}_j^6 {\hat{r}}_k^6\end{aligned}$$

(55)

$$\begin{aligned} \omega _{3,ijk}&= 16 l_i^4 {\hat{r}}_i^6 \left( {\hat{r}}_i^2 {\hat{r}}_j^2 + {\hat{r}}_i^2 {\hat{r}}_k^2 + {\hat{r}}_j^4 + {\hat{r}}_k^4 + 4 {\hat{r}}_j^2 {\hat{r}}_k^2 \right) +\ldots \nonumber \\&-\, 8 l_i^2 {\hat{r}}_i^6 \left( 4 \left( l_j^2 {\hat{r}}_j^4 + l_k^2 {\hat{r}}_k^2 \right) + 5 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( l_j^2 + l_k^2 \right) \right) +\ldots \nonumber \\&-\, 8 {\hat{r}}_i^2 {\hat{r}}_j^4 {\hat{r}}_k^4\left( 5 l_i^2\left( l_j^2 +l_k^2\right) + 16 l_j^2 l_j^2 \right) +\ldots \nonumber \\&+\, 4 l_i^4 \left( 6 {\hat{r}}_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_j^2 + {\hat{r}}_k^2 \right) + {\hat{r}}_i^2 {\hat{r}}_j^4 {\hat{r}}_k^4 \right) +\ldots \nonumber \\&-\,4 l_i^2 {\hat{r}}_i^6 \left( l_j^2 {\hat{r}}_k^4 + l_k^2 {\hat{r}}_j^4 \right) \end{aligned}$$

(56)

$$\begin{aligned} \omega _{4,ijk}&= +128 l_j^2 l_k^2 {\hat{r}}_j^4 {\hat{r}}_k^4 + 160 {\hat{r}}_i^4 l_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( l_j^2 + l_k^2 \right) +\ldots \nonumber \\&-\, l_i^4 \left( {\hat{r}}_j^4 {\hat{r}}_k^4 +\,64 {\hat{r}}_i^6 \left( {\hat{r}}_j^2+{\hat{r}}_k^2\right) \right) +\ldots \nonumber \\&-\,16 l_i^4\left( {\hat{r}}_i^8 + {\hat{r}}_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \left( {\hat{r}}_j^2+{\hat{r}}_k^2\right) \right) +\ldots \nonumber \\&+\, 4 {\hat{r}}_i^6 l_i^2 \left( 4\left( l_j^2 {\hat{r}}_k^2 + l_k^2 {\hat{r}}_j^2 \right) + 10 \left( l_j^2 {\hat{r}}_j + l_k^2 {\hat{r}}_k^2 \right) \right) \nonumber \\&+\ldots {\hat{r}}_i^4 l_j^2 l_k^2 \left( 16 \left( {\hat{r}}_j^2 + {\hat{r}}_k^2 \right) + 50 {\hat{r}}_j^2 {\hat{r}}_k^2 \right) +\ldots \nonumber \\&-\, 24 l_i^4 {\hat{r}}_i^4 \left( \left( {\hat{r}}_j^4+{\hat{r}}_k^4 \right) + 4 {\hat{r}}_j^2 {\hat{r}}_k^2 \right) \end{aligned}$$

(57)

$$\begin{aligned} \omega _{5,ijk}&= 64 l_i^2 {\hat{r}}_i^2 \left( l_i^2 {\hat{r}}_i^4 + l_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 - {\hat{r}}_i^2 \left( l_j^2 {\hat{r}}_k^2 + l_k^2 {\hat{r}}_j^2 \right) \right) +\ldots \nonumber \\&+\,32 l_i^2 {\hat{r}}_i^2 \left( 3 l_i^2 {\hat{r}}_i^2 \left( {\hat{r}}_j^2 +{\hat{r}}_k^2 \right) - 5 {\hat{r}}_i^2 \left( l_j^2 {\hat{r}}_j^2 +l_k^2 {\hat{r}}_k^2 \right) \right) +\ldots \nonumber \\&-\,200 l_j^2 l_k^2 {\hat{r}}_i^2 {\hat{r}}_j^2 {\hat{r}}_k^2 \nonumber \\&+\,\ldots 16 l_i^2 {\hat{r}}_i^2 \left( l_i^2 \left( {\hat{r}}_j^4 +\,{\hat{r}}_k^4 \right) - {\hat{r}}_i^4 \left( l_j^2 + l_k^2 \right) \right) +\ldots \nonumber \\&+\, \left( {\hat{r}}_j^2 +{\hat{r}}_k^2 \right) \left( 4 l_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 - 20 {\hat{r}}_i^4 l_j^2 l_k^2 \right) \end{aligned}$$

(58)

$$\begin{aligned} \omega _{6,ijk}&= 64 l_i^2 {\hat{r}}_i^2 \left( - l_i^2 \left( {\hat{r}}_j^2 + {\hat{r}}_k^2 \right) + {\hat{r}}_i^2 \left( l_j^2+l_k^2 \right) \right) \nonumber \\&+\,\ldots 16 l_i^2 {\hat{r}}_i^2 \left( -6 l_i^2 {\hat{r}}_i^2 + 5 \left( l_j^2 {\hat{r}}_k^2 + l_k^2 {\hat{r}}_j^2 \right) \right) +\ldots \nonumber \\&+\,4 \left( 50 l_j^2 {\hat{r}}_j^2 l_k^2 {\hat{r}}_k^2 - 4 l_i^4 {\hat{r}}_j^2 {\hat{r}}_k^2 - l_i^4 \left( {\hat{r}}_j^4+{\hat{r}}_k^4 \right) + 2 {\hat{r}}_i^4 l_j^2 l_k^2\right) \nonumber \\ \end{aligned}$$

(59)

$$\begin{aligned} \omega _{7,ijk}&= 16 \left( 4 l_i^4 {\hat{r}}_i^2 + l_i^4 {\hat{r}}_j^2 + l_i^4 {\hat{r}}_k^2 -2 {\hat{r}}_i^2 l_j^2 l_k^2 - 5 l_i^2 {\hat{r}}_i^2 \left( l_j^2 + l_k^2 \right) \right) \nonumber \\ \end{aligned}$$

(60)

$$\begin{aligned} \omega _{8,ijk}&= 16 \left( -l_i^4 + 2 l_j^2 l_k^2 \right) \end{aligned}$$

(61)