A Superposition Procedure for Calculation of Effective Diffusion and Elastic Parameters of Sparsely Porous Materials

Abstract

Effective material parameters for diffusion and elastic deformation are calculated for porous materials using a continuum theory-based superposition procedure. The theory that is limited to two-dimensional cases, requires that the pores are sufficiently sparse. The method leads to simple manual calculations that can be performed by, e.g. hospital staff at clinical diagnoses of bone deceases that involve increasing levels of porosity. An advantage is that the result relates to the bone material permeability and stiffness instead of merely pore densities. The procedure uses precalculated pore shape factors and exact size scaling. The remaining calculations do not require any knowledge of the underlying field methods that are used to compute the shape factors. The paper establishes the upper limit for the pore densities that are sufficiently sparse. A cross section of bovine bone is taken as an example. The superposition procedure is evaluated against a full scale finite element calculation. The study compares the pore induced change of the diffusion coefficient and elastic modulus. The predictions differ between superposition and full scale calculations with 0.3% points when pore contribution to the diffusion constant is 3–7%, and 0.7% points when the pore contribution to the modulus of elasticity is 4.5–5%. It is uncertain if the error is in the superposition method, which is exact for small pore densities, while the full scale finite model is not.

1 Introduction

Bone is a complex material, with a multiphase, heterogeneous and anisotropic microstructure. One of the main goals of this work is to define the relationship between bone porosity and both diffusion coefficient and elastic modulus. The reason for calculating the material parameters is that they are difficult to obtain experimentally or clinically. Further, the state of the diffusion coefficient and the modulus of elasticity may be used as a tool for clinical diagnosis. The porosity of bone can vary continuously from 2–95%, and it is usually distinguished between trabecular bone with 40–95% porosity and cortical bone with 2–20% porosity (Winkelstein 2012).

The porosity affects the diffusivity and the elastic modulus of the material. The diffusivity is important for maintaining a proper supply of nutrients and for removing waste products, while the elastic modulus determines the quality and the reliability of bone strength. Some useful models have been proposed for studies of the properties of bone tissues in the presence of pores. These are based on the poroelastic theory, in which the mechanical properties of a material are affected by the movement of the fluid in the pores (Biot 1941; Rice and Cleary 1976; Showalter 2000; Cowin 2003). In bone tissue, the transport of fluids and solutes is a concern for the bone formation and remodelling. The diffusion coefficients of different solutes in cortical bone of mammals were investigated using different techniques (Patel et al. 2004; Wang et al. 2005; Li et al. 2009; Lindberg et al. 2014). Further, the diffusion coefficients of water in trabecular bone tissue for humans were studied by Marinozzi et al. (2014a, b). The result was needed to understand the transportation process of substances on the cell level and to make realistic models for bone remodelling and bone healing.

It has been shown by Marinozzi et al. (2013) that hygroscopic driving forces lead to significant swelling of bone. The deformation compatibility that generally restricts the swelling introduces both compressive and tensile residual stresses in different parts of the bone. The stresses that counteracts the swelling, depend on the stiffness of the bone. It is, therefore, of interest also to estimate the elastic modulus and how it is affected by the pore sizes and densities.

The mechanical properties such as elastic modulus of bone are affected by the pore sizes and densities. To investigate the interrelationships between the pore size and the bone strength, several experiments are required. The relationship between the pore size and the elastic modulus may be established analytically or experimentally. The elastic modulus decreases as the pore size increases as obtained by Schaffler and Burr (1988) and Grimal et al. (2011). In Helsing and Jonsson (2002) and Helsing (2011) numerical models with the capability to compute mechanical properties of porous media containing many pores are given. The methods give accurate results without any limitations regarding pore density and shape. Also sharp corners that produce stress singularities are effectively treated.

One dimensional models Redwood et al. (1974); Safford et al. (1978); Nozad et al. (1985) and Ochoa-Tapia et al. (1994) are developed with the ambition to simplify the calculations. Two- or three-dimensional field calculations are avoided altogether. In these models the diffusion coefficient is supposed to be different in one or several subregions and the result is calculated as a series of one dimensional subregions. References to pores with real shapes are absent apart from cylindrical/spherical pores which means that the applicability is limited to nearly cylindrical/spherical pores or a wider range of shapes but randomly oriented. The assumption is based on earlier results (Perrins et al. 1979) that concern pores with random orientation. Pores in mammal bones are often irregular and not seldom crack like which affect the diffusion and the stiffness. In human long bones, the pores are often shorter in the radial direction which seriously increase the apparent diffusion coefficient and modulus of elasticity.

The use of CT-scanning of human tissues in vivo is rapidly increasing. Frequently bone is scanned to discover increased porosities. The estimation of the porosity is used for diagnoses of osteoporosis and related illnesses. It is also used to keep track of the development of diseases. However, diagnoses-based relevant parameters such as chemical permeability and stiffness should be better than simply total pore area which is used today. Moreover, the analysis can still be simple and without requiring advanced field calculations on case level. In the proposed model, only a small set of individual pores is pre-computed and is then used as references together with an exact size scaling. To this end different reference sets could be used for, e.g. female human long bones, male ditto, sets for other mammals, etc.

The present study demonstrates a simple but asymptotically exact procedure to calculate the diffusion coefficient and the elastic modulus of a material with sparse irregular pores by using superposition of known contributions to the diffusion coefficient and the modulus of elasticity. A geometry dependent correction factor is obtained for a few pore shapes along with a proper pore size scaling. The factor is based on a single finite element calculation of the local diffusive and elastic properties of a region surrounding the pore. The orientation of the pore is included as a model parameter. The method is demonstrated using a porous bovine bone sample with irregularly distributed pores. The method does not require specific knowledge of the continuum field treatment of diffusion or mechanics. However, a few precalculated parameters for some characteristic shapes need to be done. The result is compared with a full scale calculation of the same sample.

2 Theory

2.1 Diffusion

Consider a body containing a single pore. The material surrounding the pore is called the matrix. In the pore, the diffusion coefficient is set to $D_\mathrm{p}$ and in the matrix the diffusion coefficient is set to $D_\mathrm{m}$. A two-dimensional flow of matter that is driven by the concentration gradient is considered. The flow rate per unit of area, also called flux is denoted $J_{i}$, where the index denotes the direction in Cartesian coordinates $x_{i}\equiv$ {$x_{1}, x_{2}, x_{3}$}. Tensor notation including the summation rule is applied. The indices i, j assume the values 1 and 2. The flux vector $J_{i}$ of a selected substance becomes, due to differences in concentration of matter,

$$\begin{aligned} J_{i}=-D\frac{\partial c}{\partial x_{i}}, \end{aligned}$$

(1)

where c is the concentration of the flowing matter. The material parameter D is the diffusion coefficient of the substance-matrix system. Further, matter is conserved giving that

$$\begin{aligned} \frac{\partial c}{\partial t}=-\frac{\partial J_{i}}{\partial x_{i}}. \end{aligned}$$

(2)

In the present study, steady-state solutions, i.e. $\partial c/\partial t=0$ are sought. The consequence is that the flux will be divergence free, i.e.

$$\begin{aligned} \frac{\partial }{\partial x_{i}}\left( D\frac{\partial c}{\partial x_{i}}\right) =0. \end{aligned}$$

(3)

The governing Eq. (3) is solved for the boundary conditions

$$\begin{aligned} \frac{\partial c}{\partial x_{2}}=0\quad \text {at }0<x_{1}<h\text { for }x_{2}=0\text { and }x_{2}=w_{0}. \end{aligned}$$

(4)

Further,

$$\begin{aligned} c=0\quad \text {at }x_{1}=0\ \text { for }0\le x_{2}\le w_{0}\,, \end{aligned}$$

(5)

and

$$\begin{aligned} c=c_{1}\quad \text {at }x_{1}=h\ \text { for }0\le x_{2}\le w_{0}. \end{aligned}$$

(6)

Fig. 1

A thin section containing an area $h_{0}\times w_{0}$ with a pore. The average diffusion coefficient in the $h_{0}\times w_{0}$ rectangular region is $D_{0}$

At first, a thin strip of the structure is examined, see Fig. 1. The strip contains a small inserted section with the height $h_{0}$ and the width $w_{0}$, where a pore, or something else that affects the effective diffusion coefficient, is located. In this small section, the effective diffusion coefficient is set to $D_{0}$. The diffusion is assumed to be uniaxial along the boundaries of the section. The relation between $D_{0}$ and the diffusion coefficients for the matrix, $D_\mathrm{m}$, and for the pore, $D_\mathrm{p}$, and the influence of size and shape of the pore will be dealt with later in this section.

The effective diffusion coefficient $D_{1}$ for the strip is derived in the following. The total flux $J^{\prime }_\mathrm{a}$, see Fig. 1, through every cross section in the strip remains constant. Therefore according to Eq. (1)

$$\begin{aligned} D_{1}\frac{c_{1}}{h}=D_\mathrm{m}\frac{c_{1}-c_{\beta }}{h_{\beta }}=D_{0}\frac{c_{\beta }-c_{\alpha }}{h_{0}}= D_\mathrm{m}\frac{c_{\alpha }}{h_{a}}, \end{aligned}$$

(7)

applies. The concentrations $c_{\alpha }$ and $c_{\beta }$ are the concentrations on each side of the insert section as can be seen in Fig. 1. By using that $h=h_{\beta }+h_{0}+h_{\alpha }$, some algebra gives

$$\begin{aligned} D_{1}=D_\mathrm{m}\bigg (1-\bigg (1-\frac{D_\mathrm{m}}{D_{0}}\bigg )\frac{h_{0}}{h}\bigg )^{-1}. \end{aligned}$$

(8)

Fig. 2

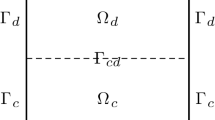
The geometry from Fig. 1 embedded in a larger section

Now a wider structure, where the strip is being an insert, is considered, see Fig. 2. By introducing an effective diffusion coefficient $D_\mathrm{e}$ for the entire structure, the average flow through the entire structure is described as

$$\begin{aligned} J_\mathrm{a}=-D_\mathrm{e}\frac{c_{2}}{h}. \end{aligned}$$

(9)

Uniaxial flow is again assumed for along the boundaries of the strip with the width $w_0$. The requirement is again that the pore should be sufficiently small for this to be an acceptable assumption. According to Fig. 2, it is then obvious that the total amount of matter that passes a cross section of the structure is

$$\begin{aligned} J_\mathrm{a}w=-D_{1}\frac{c_{2}}{h}w_{0}-D_\mathrm{m}\frac{c_{2}}{h}(w-w_{0}), \end{aligned}$$

(10)

where the first term on the right-hand side represents the flux through a cross section of the inserted strip with the width $w_{0}$. The second term is the remaining part of the total flux through matrix material. If Eq. (8) is used to express $D_{1}$ in given quantities and Eqs. (9) and (10) are used to eliminate $J_\mathrm{a}$ and $c_{2}$, then the effective diffusion coefficient is obtained as

$$\begin{aligned} D_\mathrm{e}=D_\mathrm{m}\left( 1+\frac{1-D_\mathrm{m}/D_{0}}{1-(1-D_\mathrm{m}/D_{0})\frac{h_{0}}{h}}\frac{h_{0}w_{0}}{hw}\right) . \end{aligned}$$

(11)

The derived scaling $h_{0}w_{0}/hw$ relates the rectangular area, $h_{0}w_{0}$, to the area of the full body, hw. The quantities defining $D_\mathrm{e}$ are the height ratio $h_{0}/h$, the area ratio $h_{0}w_{0}/hw$ and the ratio of the diffusivity coefficients, $D_\mathrm{m}/D_{0}$.

Since the derivation leading to Eq. (11) did not explicitly utilise the shape of the region $h_{0}\times w_{0}$ it is here assumed that the result Eq. (11) can be used also for pores of general shape. Therefore, the diffusivity inside the pores is given by the diffusion coefficient, $D_\mathrm{p}$. Further, the quantity $h_{0}w_{0}$ in Eq. (11) is replaced with $\theta A_\mathrm{p}$, where $A_\mathrm{p}$ is the pore area in the $x_{1}-x_{2}$ plane, and $\theta$ is a geometrical factor that apart from shape and size of the pore also depends on the orientation of the pore with respect to the nominal flow direction. Finally, the relative height $h_{0}/h$ in Eq. (11) is replaced with $\sqrt{A_\mathrm{p}/hw}$, and a shape correction factor $\kappa$. As a consequence, the following two relations replace Eq. (11), and $D_\mathrm{e}$ is written

$$\begin{aligned} D_\mathrm{e}=D_\mathrm{m}\bigg (1+\frac{\theta s}{1-\kappa s\sqrt{\frac{A_\mathrm{p}}{hw}}}\ \frac{A_\mathrm{p}}{hw} \Big ), \end{aligned}$$

(12)

where the relation between $D_\mathrm{m}$ and $D_\mathrm{p}$ for convenience is represented by the quantity

$$\begin{aligned} s=1-\frac{D_\mathrm{m}}{D_\mathrm{p}}. \end{aligned}$$

(13)

The values $\theta$ and $\kappa$, must be established. In order to do so Eq. (12) is expanded as a power series of $\sqrt{A_\mathrm{p}/hw}$ as

$$\begin{aligned} \left( \frac{D_\mathrm{e}}{D_\mathrm{m}}-1\right) \frac{hw}{sA_\mathrm{p}}=\theta \left[ 1+ \kappa s\sqrt{\frac{A_\mathrm{p}}{hw}}+ (\kappa s)^{2}O\left( \frac{A_\mathrm{p}}{hw}\right) \right] . \end{aligned}$$

(14)

Finite element calculations for the current pore shape are done for different pore sizes $A_\mathrm{p}$, as described in Sect. 3. By studying the flux, it is now possible to determine $\theta$ and $\kappa$ from the two leading terms of the right-hand side of Eq. (14). The parameters are obtained through least square fit. The determination of $\theta$ and $\kappa$ is done for a range of pore sizes and the limiting values for vanishing pore sizes are sought. The procedure is performed for relevant pore shapes and orientations relative to the direction of the flux.

The effective diffusion coefficient $D_\mathrm{e}$ of the entire structure is defined as

$$\begin{aligned} D_\mathrm{e}=-J_\mathrm{a}\frac{h}{c_{o}}, \end{aligned}$$

(15)

where $c_\mathrm{o}$ is the prescribed concentration at $x_{1}=h$ and $J_\mathrm{a}$ is the average flux through the body calculated as

$$\begin{aligned} J_\mathrm{a}=\frac{1}{w}\int _{0}^{w}J_{1}\text {d}x_{2}\ \quad \text {at}\ x_{1}=h, \end{aligned}$$

(16)

where $J_{1}$ is the flux in the $x_{1}$-direction, cf. Eq. (1). The effective diffusivity coefficient $D_\mathrm{e}$ can be calculated for bodies with large geometries and multiple pores. It is obvious from the analysis above that as long as the individual pores do not interact, the result is found using superposition of the individual contributions from each pore. This is supposed to be possible if the pores are sufficiently small as compared with the distance between the pores. The following is used,

$$\begin{aligned} D_\mathrm{e}=D_\mathrm{m}\bigg (1+\frac{s}{hw}\ \sum _{i=1}^{N}\,\frac{{\tilde{\theta }}^{(i)}A_\mathrm{p}^{(i)}}{1-s\kappa ^{(i)}\sqrt{\frac{A_\mathrm{P}^{(i)}}{hw}}}\bigg ), \end{aligned}$$

(17)

where summation is performed for N pores. The geometry factors ${\tilde{\theta }}^{(i)}$ and $\kappa ^{(i)}$ are chosen as the result of $\theta$ and $\kappa$ for sufficiently small pore sizes and are selected as the one of a limited set of representative pores. By studying the pores in a region of the material specimen which is believed to be representative for the total specimen, and follow the procedure just described, the total $D_\mathrm{e}$ for the specimen can be established using Eq. (17).

2.2 Elastic Theory

In this section, a method to compute how present pores influence the elastic modulus is presented. The same geometries and pores as above are assumed. To follow the conventional tensor notation, the stresses are written $\sigma _{ij}$, the strains $\epsilon _{ij}$ and the displacements $u_{i}$. The stresses are given by Hooke’s law as

$$\begin{aligned} \sigma _{ij}=\frac{E}{1+\nu }\left( \epsilon _{ij}+\frac{\nu }{(1-2\nu )}\delta _{ij}\epsilon _{kk}\right) \end{aligned}$$

(18)

and the strains $\epsilon _{ij}$, which are assumed to be small, are defined by

$$\begin{aligned} \epsilon _{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}). \end{aligned}$$

(19)

The equations of equilibrium, $\sigma _{ij,j}=0$, after insertion of Eqs. (18) and (19) give the equation

$$\begin{aligned} u_{i,jj}+\frac{1}{1-2\nu }u_{j,ij}=0. \end{aligned}$$

(20)

Equation (20) governs the linear elastic behaviour of the body. For stretching in the $x_{1}$-direction, the boundary conditions are

$$\begin{aligned} u_{1}=0\quad \text {at}\quad 0\le x_{2}\le w\quad \text {for}\quad x_{1}=0 \end{aligned}$$

(21)

and

$$\begin{aligned} u_{1}=\delta \quad \text {at}\quad 0\le x_{2}\le w\quad \text {for}\quad x_{1}=h. \end{aligned}$$

(22)

Normal tractions on the remaining edges $x_{2}=0, 0<x_{1}<h$ and $x_{2}=w, 0<x_{1}<h$ vanish. Finally, shear tractions on all edges vanish.

The average tractions at $x_{1}=h$ are calculated as

$$\begin{aligned} \sigma _\mathrm{a}=\frac{1}{w}\int _{0}^{w}\sigma _{11}\text {d}x_{2}. \end{aligned}$$

(23)

The effective modulus of elasticity is defined as

$$\begin{aligned} E_\mathrm{e}=\sigma _\mathrm{a}\frac{h}{\delta }. \end{aligned}$$

(24)

The presence of pores will weaken the structure, whereas the stiffness of the pore material, being a fluid, is assumed to be insignificant. It seems reasonable that the weakening may be ignored at large distance from the pore. It is also assumed that the linear extent of this region scale with the width of the pore b perpendicular to the loading direction. As for the diffusion case the change of the modulus of elasticity is assumed to be proportional to the area of the pore. To make it possible to include a crack, the square of the linear extent in the direction perpendicular to the nominal loading direction versus the body area is selected as the scaling parameter. The assumption is verified for a crack and a circular pore, see “Appendix”. In the same way as for the diffusion theory a geometry factor $\theta _\mathrm{E}$ is included for the influence of other geometrical details of the pore apart from the width b. This leads to the first order approximation

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{m}\bigg (1-\theta _\mathrm{E}\frac{b^{2}}{hw}\Big ) \end{aligned}$$

(25)

for loading in the $x_{1}$-direction. To obtain the geometry factor $\theta _\mathrm{E}$, numerical values of $E_\mathrm{e}$ for single pore geometries for different pore sizes are calculated using the finite element method. A power expansion for small pores gives the expression

$$\begin{aligned} \left( \frac{E_\mathrm{e}}{E_\mathrm{m}}-1\right) \frac{hw}{b^{2}}=\theta _\mathrm{E}+O\left( \frac{b^{2}}{hw}\right) , \end{aligned}$$

(26)

where $E_\mathrm{m}$ is the modulus of elasticity of the matrix material. The value $\theta _\mathrm{E}$ is fitted to the numerical result of $E_\mathrm{e}$ for different pore shapes and orientations and by taking vanishing pore size result. Details are given in Sect. 3.

For a large body with multiple pores, the effective modulus of elasticity, $E_\mathrm{e}$, may be calculated using the same superposition principle as for the diffusion case, cf. Eq. (17). The calculation is performed as

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{m}\bigg (1-\frac{1}{hw}\sum _{i=1}^{N}\theta _\mathrm{E}^{(i)} \left( b^{(i)}\right) ^{2}\Big ), \end{aligned}$$

(27)

where the summation is performed for N pores. The geometry factors $\theta _\mathrm{E}^{(i)}$ are chosen for sufficiently small pores and for a corresponding shape.

By studying the pores in a region of the material specimen that is believed to be representative for the total specimen, if necessary by using statistics, and following the procedure just described, the total $E_\mathrm{e}$ for the specimen can be established employing Eq. (27).

3 Numerical Analysis

The scanned bone images are transferred to a mesh that is used for finite element calculations. This is done in two steps. First a CAD program is used to create an intermediate object mesh that describes the cross section of the bone sample (see an example in Fig. 3). Smaller sections of the object mesh, each containing a pore, are then transferred to the finite element program ABAQUS (2014) and covered by isoparametric elements in a preprocessor. ABAQUS offers the possibility to compute elastic deformation and steady-state diffusion. Equation (3) is the governing equation for diffusion and Eq. (20) is the governing equation for deformation. The boundary value problem is solved for the region $0\le x_{1}\le h$ and $0\le x_{2}\le w$ using a free mesh composed of trilateral 6-node and quadrilateral 8-node isoparametric elements. Full integration is used. For each type of pore geometry, same element mesh is used for both the diffusion and the deformation problem. A representative case is shown in Fig. 4.

Fig. 3

a An original image of a typical pore with a linear extent of around 35 $\upmu$m. The linear extent of the cubic voxels is $4.2\,\upmu \text {m}$. b The geometry as a prepared object mesh using a 50% greyscale threshold. The object mesh is in a last step transformed into a mesh of 6-node and 8-node isoparametric elements

Fig. 4

A typical mesh. Here for pore C$^{\prime }$ and with $h/a=w/b=2$. The pore is the central grey area. In the original image, the pore covers $6\times 9$ pixels. The meshed area $hw=97\times 57\,\upmu \text {m}^2$

Fig. 5

a A $0.22\times 0.20\,\text {mm}^2$ part of a $10\times 10\,\text {mm}^2$ bovine ulna sample (Ståhle et al. 2013). A 50% greyscale threshold has been used (cf. Fig. 4a, b). The pores A, B, C, and D are used as reference cases. Evaluation is then performed on the region with numbered pores in the lower right corner of the image marked with dashed edges. b Detailed view of the selected pores

The ratio of the linear extent of adjacent elements is never more than 2 and normally around 1.2. The meshes for the different pore geometries are built up of eight to ten thousand nodes and two to three thousand six-node and eight-node isoparametric plane elements.

4 Establishing Material Parameters

The procedure is evaluated using a sample of bovine ulna. A single CT scan image of the bone sample is used, see Fig. 5. The image is produced by Ståhle et al. (2013). The original image is a $10\times 10$ mm$^{2}$ cross section of an around $10\times 10\times 30$ mm$^{3}$ bone specimen from a bovine ulna. It shows traces of multiple cracks that almost inevitably occur in bone samples as soon as they are exposed to air. The $x_{1}$-axis goes from the endosteum (i.e. the inner surface of the bone, facing towards the bone marrow) in the radial direction out to the periosteum (i.e. the outer surface of the bone). The $x_{2}$-axis is along the tangential direction of the bone cross section. The longitudinal direction along the ulna is perpendicular to the plane of the image in Fig. 4.

The four pores marked A to D are assumed to be a fair representation of the various shapes that are present in the segment of the bone cross section, cf. Fig. 5a. Images showing the geometrical details of the selected pores are shown in Fig. 5b. By rotating the pores $90^{\circ }$ an additional set of pores A$^{\prime }$ to D$^{\prime }$ are obtained. Apparent values of $\theta , \kappa$ and $\theta _\mathrm{E}$ are obtained for small pore sizes. Convergent values for the set of parameters were obtained in all cases.

The height of the pores, a, is along the direction of the nominal flux or load, and the width, b, is perpendicular to that. The ratio a / b is from 0.38 for pore A to 2.67 for pore A$^{\prime }$, see Table 1. The unit of length is a pixel, that is 4.2 $\upmu$m. The voxel depth is also a unit making a cubic shape with the length of each side of 4.2 $\upmu$m.

Table 1 Data for the pores A to D and their counterparts A$^{\prime }$ to D$^{\prime }$ that are rotated $90^{\circ }$

4.1 Diffusion Coefficient Results

The content of the pores is assumed to have diffusive and mechanical properties similar to water. Diffusion coefficients of a large number of substances in water are listed in the book (Cussler 1997). With only a few exceptions, the diffusion coefficients are in the range $1\times 10^{-9}$–$3\times 10^{-9}$ m$^{2}$/s and the diffusion coefficient in the pore is here taken to be $D_{p}=2\times 10^{-9}$ m$^{2}$/s. Patel et al. (2004) studied diffusion of different molecules in bovine bone. They found that the diffusivity varied considerably when measured on tissue level, cellular syncytium level and matrix microporosity level. On the matrix microporosity level, the diffusion coefficient was found to be close to $1\times 10^{-13}$ m$^{2}$/s for a molecule mass of 300 atomic mass units (u). Therefore, the calculations in the present study are performed for a ratio of the diffusion coefficient in water versus that in bone of $D_\mathrm{p}/D_\mathrm{m}=2\times 10^{4}$.

Fig. 6

Distribution of the concentration. The nominal flux is vertical. The contour shows pore C$^{\prime }$ with an around 20,000 times larger diffusion constant than the surrounding bone

Fig. 7

Normalised average flux $J_{a}h/(D_\mathrm{m}{\Delta } c)$ for pores A ($\square$), B ($\circ$), C ($\triangle$) and D ($\times$) (solid lines) and A$^{\prime }$ to D$^{\prime }$ with corresponding markers and dashed lines, as a function of the pore size $\sqrt{A_\mathrm{p}/hw}$

The distribution of the normalised concentration inside the computed region is shown in Fig. 6. The geometry corresponds to the one found in Fig. 6. The pore C$^{\prime }$ is displayed as the dashed curve. The extent of the geometry is $h\times w$. The side ratio of the geometry is the same as the ratio of the pore size meaning that $a/b=h/w$. The extent of the area of the pore versus that of the geometry is $A_\mathrm{p}/hw=0.09$. One readily observes how the flux in the neighbourhood of the pore diverts from uniaxial flux and approaches the pore.

The colours represent constant concentration. The increased diffusion rate in the neighbourhood of the pore reveals itself as an increase of the distances between the colour contours. The flux direction is perpendicular to the concentration levels as indicated by the inserted arrows. The diffusion, which nominally flows in the $x_{1}$-direction, is observed to be diverted towards the pore. Obviously, the increased diffusion rate also increases in a region surrounding the pore. Close to all four edges of the geometry, the diffusion is less affected by the presence of the pore. The affected region seems to be a few times the extent of the pore (see Fig. 6).

The calculated normalised average flux, $J_\mathrm{a}h/(D_\mathrm{m}{\Delta } c)$, where ${\Delta } c$ is the difference in concentration between $x_{1}=0$ and $x_{1}=h$ for different flow directions and different pore sizes, is displayed in Fig. 7. The nominal flux, i.e. the flux for $\sqrt{A_\mathrm{p}/hw}=0$ is $J_\mathrm{a}h/(D_\mathrm{m}{\Delta } c)=1$. It is seen that the flux as expected increases with increasing pore sizes. As an example, when the area of the pore is 30% of the total area hw, i.e. $\sqrt{A_\mathrm{p}/hw}=0.55$, the flux is in the region of around 5–8% larger than the nominal flux in the absence of a pore. When the area of the pore is 40% of the total area hw, the flux is as much as two times the nominal flux.

The interaction between the ratio of the pore size versus the linear body size $\sqrt{A_\mathrm{p}/hw}$ in terms of its influence on the geometry factor $\theta$ is shown in Fig. 8. An interesting observation is that $\theta$ is practically constant for pores smaller than $\sqrt{A_\mathrm{p}/hw}<0.3$. The meaning is that the value for very small pores is applicable as long as the linear size of the pore is less than a third of the linear size of the body, or to be more precise, the calculated cell hw. For application purposes, this would be replaced with the distance to the nearest pore.

Fig. 8

The geometry factor $\theta$ for pores A ($\square$), B ($\circ$), C ($\triangle$) and D ($\times$) (solid lines) and A$^{\prime }$ to D$^{\prime }$ with corresponding markers and dashed lines, as a function of the relative pore size $\sqrt{A_\mathrm{p}/hw}$

To utilise this, the small pore value of the geometry factor $\theta$ is denoted ${\tilde{\theta }}$ and is defined as,

$$\begin{aligned} {\tilde{\theta }}=\lim _{\sqrt{\frac{A_\mathrm{p}}{hw}}\rightarrow 0}\theta . \end{aligned}$$

(28)

The limit value, ${\tilde{\theta }}$ is a pure shape factor and is independent of the relative size of the pore $A_\mathrm{p}/hw$. To achieve reliable results, the numerical values for $\theta$, which are vitiated with scatter, are least square fitted using the first four terms of a series expansion of $\theta$ as it is obtained for different pore sizes, as described in Sect. 2. A Matlab function that employs the least square fit is used to find the leading term. The obtained factors ${\tilde{\theta }}, \kappa$ and ${\tilde{\theta }}_\mathrm{E}$ are given in Table 2.

Table 2 ${\tilde{\theta }}, \kappa$, and ${\tilde{\theta }}_\mathrm{E}$ values for the pores A to D and A$^{\prime }$ to D$^{\prime }$

Figure 9 summarises the values of ${\tilde{\theta }}$ as a function of the pore aspect ratio a / b. The figure shows that ${\tilde{\theta }}$ increases with increasing a / b. The result from a series of six rectangular pores is included. The rectangular pores has a smaller scatter which indicates that there are more influential possibly mesh related details, regarding the shape than merely the aspect ratio.

Fig. 9

${\tilde{\theta }}$ versus the shape ratio a / b for pores A to D and A$^{\prime }$ to D$^{\prime }$ ($\times$). ${\tilde{\theta }}$ for six rectangular pores with $a/b=2.5,2,1.5,1,0.67,0.5$ are also included ($\square$). The result for a circular pore is included (Ochoa-Tapia et al. 1994)

4.2 Elastic Modulus Results

Calculation of the elastic modulus of a region containing a single pore is performed along the same lines as for the diffusion analysis. The modulus of elasticity of the matrix is $E_\mathrm{m}$ and Poisson’s ratio is $\nu =0.3$. The displacement difference of two opposed edges, separated by the distance h, is $\delta$. Plane stress is assumed. The material in the pore is assumed to lack stiffness, meaning that the body is treated as a hollow section.

Fig. 10

Distribution of the largest principal stress $\sigma _{1}h/E_\mathrm{m}{\Delta } u$ for pore C$^{\prime }$ with $a/b=1.5$. The nominal loading is in the $x_{1}$-direction

The distribution of the normalised largest principal stress $\sigma _{1}h/E_\mathrm{m}\delta$ for pore C$^{\prime }$, for which $a/b=1.5$, is shown in Fig. 10. The figure shows that stresses are high at two points on the edges of the pore. Here, the stress is expected to be high but is probably overestimated because of the rather coarse mesh that is used in the vicinity of the pore. The pore geometry is obtained from the CT scanned bone sample as displayed in Fig. 4. Due to the small dimensions of the pore of only $6\times 9$ pixels, the details of the pore are by necessity rather edgy. The shape is obtained from a 50% greyscale threshold and interpolation between the pixels. The process removes the original zig-zag contour but leaves some sharp corners (cf. Fig. 3).

The stress distribution along the edges of the body is fairly homogeneous and close to the nominal value $\sigma _{1}h/E_\mathrm{m}\delta =1$, which shows that the disturbance of the remote uniaxial stress field is more or less localised to a fairly small region around the pore.

Fig. 11

Computed average normalised stress $\sigma _\mathrm{e}/\sigma _\mathrm{m}$ for pores A ($\square$), B ($\circ$), C ($\triangle$) and D ($\times$) (solid lines) and A$^{\prime }$ to D$^{\prime }$ with corresponding markers and dashed lines, for different pore sizes $\sqrt{A_\mathrm{p}/hw}$. $\sigma _\mathrm{m}$ is the stress in the matrix without a pore

The average stress, $\sigma _\mathrm{e}/\sigma _\mathrm{m}$, for different loading directions and different pore sizes is shown in Fig. 11. The nominal stress is defined as $\sigma _\mathrm{m}=E_\mathrm{m}\delta /h$. The effective stress $\sigma _\mathrm{e}$ is obtained from the finite element calculations. As expected, the figure shows that the stress decreases as the pore size increases. For large pores ($b/\sqrt{hw}>0.3$), the resulting stress decays approximately linearly with $b/\sqrt{hw}$. Obviously, the stress should become zero at $b/h=1$ when the entire body is transversed by the pore which decreases the stiffness to zero.

The shape factor ${\tilde{\theta }}_\mathrm{E}$ is defining the influence of pores of infinitesimal size. As for the diffusion case, the estimated value of the geometry factor is denoted $\theta _\mathrm{E}$. Following Eq. (25) the definition is

$$\begin{aligned} \theta _\mathrm{E}=\left( 1-\frac{E_\mathrm{e}}{E_\mathrm{m}}\right) \frac{hw}{b^{2}}. \end{aligned}$$

(29)

Fig. 12

Influence factor $\theta _\mathrm{E}$ for pores A ($\square$), B ($\circ$), C ($\triangle$) and D ($\times$) (solid lines) and A$^{\prime }$ to D$^{\prime }$ with corresponding markers and dashed lines, for different pore sizes $b/\sqrt{hw}$

The obtained $\theta _\mathrm{E}$ for different $b^{2}/hw$ values is shown in Fig. 12. As shown in the figure, the resulting $\theta _\mathrm{E}$ is dependent on the pore shape and size. Further, $\theta _\mathrm{E}$ decreases as the pore size increases which is an expected consequence of the switch off behaviour of the pore size dependence described in the previous paragraph. The limiting value for small pores is

$$\begin{aligned} {\tilde{\theta }}_\mathrm{E}=\underset{\frac{b^{2}}{hw}\rightarrow 0}{\lim }\theta _\mathrm{E}{}. \end{aligned}$$

(30)

Fig. 13

${\tilde{\theta }}_\mathrm{E}$ versus the shape ratio a / b for pores A to D$^{\prime }$ with markers $\times$. The ${\tilde{\theta }}_\mathrm{E}$ for six rectangular pores with side ratios $a/b=2.5,2,1.5,1,0.5,0.67$ are also presented here with markers $\square$. The side length is a in the direction of the load. The known limit result as $a/b\rightarrow$0, i.e. for a crack, with ${\tilde{\theta }}_\mathrm{E}=\frac{\pi }{2}$ and for a circular hole, ${\tilde{\theta }}_\mathrm{E}=\frac{3\pi }{4}$ with $a/b=1$ are included

The obtained ${\tilde{\theta }}_\mathrm{E}$ for pores A to D$^{\prime }$ and the rectangular pores versus the ratio a / b is shown in Fig. 13. In Table 2 ${\tilde{\theta }}_\mathrm{E}$ is listed for pores A to D$^{\prime }$. A couple of diverging results are observed. Both are for the slender pores A and C when the nominal stress is along the longest side of the pore, which is b for both. It is known from crack mechanics that energy released at the introduction of a crack vanishes for a crack that is parallel with the loading direction and reaches a maximum if the crack is perpendicular to the loading direction. The exact result as derived in the Appendix, ${\tilde{\theta }}_\mathrm{E}=\pi /2$ for a crack and ${\tilde{\theta }}_\mathrm{E}=3\pi /4$ for a circular pore, is added to Fig. 13. The result is obtained by using the analytical solution for an infinite stretched plane body with a circular hole cf. (Muskhelishvili 1953). For pores with $a>b$, the nominal stress is parallel with the longer side of the body, while Eq. (25), that defines the $\theta _\mathrm{E}$, only involves the pore width b. This inadvertence might be the reason for the observed influence on the results.

5 Qualifying Examples

The method is qualified by applying the superposition technique on real cases for diffusion coefficients and elastic moduli. The porous region of the image in Fig. 5 is chosen. The region is recognised as the region with pores labelled A and 1 to 11, framed in the dashed rectangle. Finite element calculations were performed using 17 682 8-node isoparametric elements.

The diffusion coefficient was found to be $D_\mathrm{e,FEM} = 1.033D_\mathrm{m}$ in the radial ($x_1$) direction, and $1.071D_m$ in the tangential ($x_2$) direction. This is compared with the superposition technique using (17), where values for the characteristic shapes were determined using FEM, and are listed in Table 2. The resulting $D_\mathrm{e,sup}=1.030D_\mathrm{m}$ in the radial direction and $1.068D_\mathrm{m}$ in the tangential direction.

The numerically calculated elastic modulus was found to be $E_\mathrm{e,FEM} = 0.895E_\mathrm{m}$ in the radial direction and $0.955E_\mathrm{m}$ in the tangential direction. The superposition technique gives $E_\mathrm{e,sup}=0.889E_\mathrm{m}$ and $0.948E_\mathrm{m}$ in the radial and the tangential directions, respectively. In both cases, the superposition method gives smaller moduli than the finite element method.

The reason for these differences regarding diffusion coefficient and elastic modulus is for the presence somewhat unclear. For the superposition model, applied in both radial and tangential directions, the increase of the diffusion coefficients due to the pores is 0.3% points less, while the decrease of the elastic moduli is 0.7% points more than the FEM result (see Table 3. The expectations from the result displayed in Figs. 8 and 12 where the real diffusion coefficients are larger and the elastic moduli are smaller for larger pore densities excludes the possibility that the deviations should be caused by a too small mesh to pore size ratio. Another possibility is that the meshing of the regions between the cells with pores where the flux and stress, in the superposition model is supposed to be uniaxial. The uniaxial field should be modelled with a very high accuracy, if not with machine precision. On the other hand, 0.7 and 0.3% is normally considered to be rather good for being a FEM result.

Finite element approximations are known to give a upper bound for the stiffness when full integration is performed, as is done here. At prescribed displacements and concentrations, stress and flux is overestimated which leads to an overestimation of $D_\mathrm{e}$ and $E_\mathrm{e}$. It is also worth noting that the result in this respect is the same in both radial and tangential directions, which could indicate a relatively weak dependence of the pore shape and orientation. The latter could implicate that the superposition results are the most accurate. A definite answer regarding the accuracy requires further studies of more examples with a variation of pore densities.

The differences between the FEM results and the superposition model as fractions of the rather small pore induced changes are between 4 and 16%. Considering this it is important to realise that the obtained results should be used with caution especially at low pore densities.

Table 3 Superposition and FEM results compared, for diffusion and elastic deformation

6 Conclusions

Superposition principles are derived that employ dimensional scaling of material parameters. The correction asymptotically is exact for small pore sizes. In the present study, the error is found to be less than 10% of the pore correction of the diffusion coefficient if $\sqrt{A_\mathrm{p}/hw}<0.3,$ and 10% of the correction of the modulus of elasticity if $b/\sqrt{hw}<0.1$ (cf. Figs. 8, 12).

In the present analysis, the pores have width to height ratios w / h in the range 0.37–2.7. The difference between a the pore influence on the effective diffusion coefficient and the modulus of elasticity is of the order of 2.5, cf. Figs. 9 and 13.

The method is evaluated for a sample of bovine ulna for both the diffusion and deformation cases. The superposition results are compared with full scale finite element results. Specifically, the change of the diffusion coefficient and the change of the elastic modulus due to the presence of pores, are compared with the corresponding finite element results. The change of the diffusion coefficient is 3–7% depending of the direction of the flux. The change of the modulus of elasticity is 5–11% depending on the loading direction.

Compared with finite element results a difference of 0.3% of the diffusion coefficient and of 0.7% of the modulus of elasticity is found. Relative to the correction itself the difference make up 4–16%. The reason for the differences between the two models is discussed considering that the requirements that the pores should be sparse is well fulfilled. A possible reason could be that the smallness of the correction amplifies expected errors of the finite element calculation. A support is found in the fact that the superposition is definitely leading to the trivial result $D_\mathrm{e, sup}=D_\mathrm{m}$ and $E_\mathrm{e, sup}=E_m$ for vanishing pores, whereas the finite element result may depend on the element size and the irregular mesh that is produced by the finite element preprocessor, cf. (ABAQUS 2014).

Appendix: Using the M-Integral

The reduction of the stiffness of a large panel with a circular hole or a crack through its thickness is calculated using the path independent M-integral. The integral is based on a conservation law applicable to elastostatics that was obtained by Knowles and Sternberg (1972). The integral is a function of the stress and displacement gradient field. As a consequence of the path independence, it vanishes for a closed loop path bounding a regular region. Opposed to that, integration along a closed loop bounding a non-regular region, e.g. a region containing a pore, such as a hole or a crack, does generally not vanish. Budiansky and Rice (1970) showed that in this case the M-integral can be interpreted as the potential energy release rate associated with an expansion of the region. For more details regarding the M-integral cf. (Freund 1978). Expand in this context means a scaling of all geometrical characteristics. From the energy release rate follows the change of the stiffness of the structure.

The value of M is defined by the line integral

$$\begin{aligned} M=\int _{\varOmega }\left( Wn_{i}-T_{j}\frac{\partial u_{j}}{\partial x_{i}}\right) x_{i}\text {d}{\varGamma }\,, \end{aligned}$$

(31)

where W is the elastic energy density, $n_{i}$ is the unit normal to $\varOmega$ which is directed to the right relative to the direction of the path ${\varGamma }$ in the $x_{1}$-$x_{2}$ plane, $T_{i}$ are the tractions acting on the material to the left of $\varOmega$ relative to the direction of ${\varGamma }$ and $u_{i}$ are the displacements. The elastic strain energy density is defined by

$$\begin{aligned} W=\frac{1}{2}\sigma _{ij}\epsilon _{ij}\,, \end{aligned}$$

(32)

where the stress components $\sigma _{ij}$ are related to the strain components $\epsilon _{ij}$ via Hooke’s law. The path independence of M in Eq. (31) follows directly from a corresponding conservation law (cf. Budiansky and Rice 1970).

Consider a stretched large plane panel with height h and width w so that $0\le x_{1}\le h$ and $0\le x_{2}\le w$ in a Cartesian coordinate system as shown in Fig. 14. The pore is here either a circular hole with the diameter b or a crack with the length b. The stretching is given as a constant displacement $u_{1}=\delta$ of the edge at $x_{1}=h$. The displacement $u_{1}=0$ along the edge at $x_{1}=0$. Remaining boundary conditions are absence of tractions along all edges. Without loss of generality plane stress is assumed.

Fig. 14

a Integration path for a panel with a crack. b Same for a panel with a circular hole

The integration loop is divided into eight segments, $\varOmega _{1}$ to $\varOmega _{8}$, that form a closed loop encompassing a regular region, see Fig. 14. The contributions $M_{1}$ to $M_{8}$ from integration over the corresponding segments add up to

$$\begin{aligned} M_{1}+M_{2}+\cdots +M_{8}=0. \end{aligned}$$

(33)

The contributions are defined as

$$\begin{aligned} M_{N}=\int _{\varOmega _{N}}\left( Wn_{i}-T_{j}\frac{\partial u_{j}}{\partial x_{i}}\right) x_{i}\text {d}{\varGamma }\ \ \text {for}\ \ N=1,\ldots ,8. \end{aligned}$$

(34)

Because of the reversed direction of both the outward normals and the tractions, the contributions from the integration along $\varOmega _{2}$ and $\varOmega _{8}$ annulate each other, i.e. $M_{2}+M_{8}=0$.

On segments $\varOmega _{3}$ and $\varOmega _{7}$: $x_{2}=w$ , $n_{1}=0, n_{2}=-1,$ $T_{1}=T_{2}=0$, and $\text {d}{\varGamma }=-\text {d}x_{1}$ which gives

$$\begin{aligned} M_{3}+M_{7}=-\frac{w}{2E_\mathrm{b}}\int _{0}^{h}\sigma _{11}^{2}\text {d}x_{1}. \end{aligned}$$

(35)

On segment $\varOmega _{4}$: $x_{1}=0, n_{2}=0,$ $T_{2}=0$, and $u_{1}=0\ \Rightarrow \ \partial u_{1}/\partial x_{2}=0$, which gives

$$\begin{aligned} M_{4}=0. \end{aligned}$$

(36)

On segment $\varOmega _{5}$: $x_{2}=0$ , $n_{1}=0$, and $T_{1}=T_{2}=0$, which gives

$$\begin{aligned} M_{5}=0. \end{aligned}$$

(37)

Finally on segment $\varOmega _{6}$: $x_{1}=h, n_{1}=-1, n_{2}=0,$ $T_{1}=-\sigma _{11}, T_{2}=0, \partial u_{1}/\partial x_{1}=\epsilon _{11}=(\sigma _{11}-\nu \sigma _{22})/E_\mathrm{b}, \partial u_{1}/\partial x_{2}=0$, and $\text {d}{\varGamma }=\text {d}x_{2}$ which gives

$$\begin{aligned} M_{6}=\frac{h}{2E_\mathrm{b}}\int _{0}^{w}\left( \sigma _{11}^{2}-\sigma _{22}^{2}\right) \text {d}x_{2}. \end{aligned}$$

(38)

Now Eq. (33) reduces to

$$\begin{aligned} M_{1}=-M_{3}-M_{7}-M_{6}\,, \end{aligned}$$

(39)

which reads

$$\begin{aligned} M_{1}=\frac{w}{2E_\mathrm{b}}\int _{0}^{h}\left\{ \sigma _{11}^{2}\right\} _{x_{2}=w}\text {d}x_{1}-\frac{h}{2E_\mathrm{b}}\int _{0}^{w}\left\{ \sigma _{11}^{2}-\sigma _{22}^{2}\right\} _{x_{1}=h}\text {d}x_{2}. \end{aligned}$$

(40)

By splitting the stresses into

$$\begin{aligned} \sigma _{11}=\sigma _\mathrm{o}+{\Delta }\sigma _{11}\,\text {and}\,\sigma _{22}={\Delta }\sigma _{22}\,, \end{aligned}$$

(41)

where $\sigma _\mathrm{o}$ is the stress in a homogeneous panel and ${\Delta }\sigma _{11}$ and ${\Delta }\sigma _{22}$ are stresses that arise because of the pore, in this case the circular hole or the crack. Since the pore is supposed to be small as compared to the extent of the panel the result is that ${\Delta }\sigma _{11}/\sigma _\mathrm{o}\ \text {and}\ {\Delta }\sigma _{2}/\sigma _\mathrm{o}\ \rightarrow 0$. After excluding second-order terms of Eq. (40), it follows that

$$\begin{aligned} M_{1}=\frac{\sigma _\mathrm{o}}{E_\mathrm{b}}\left\{ w\int _{0}^{h}\left\{ {\Delta }\sigma _{11}\right\} _{x_{2}=w}\text {d}x_{1}-h\int _{0}^{w}\left\{ {\Delta }\sigma _{11}\right\} _{x_{1}=h}\text {d}x_{2}\right\} . \end{aligned}$$

(42)

Per definition Eqs. (24) and (23) give

$$\begin{aligned} E_\mathrm{e}=\frac{h}{\delta w}\int _{0}^{w}\left\{ \sigma _{11}\right\} _{x_{1}=h}\text {d}x_{2}. \end{aligned}$$

(43)

Using that the nominal stress $\sigma _\mathrm{o}=\frac{\delta }{h}E_\mathrm{b}$ gives

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{b}-\frac{h}{\delta ^{2}w}M_{1}+\frac{1}{\delta }\int _{0}^{h}\left\{ {\Delta }\sigma _{11}\right\} _{x_{2}=w}\text {d}x_{1}. \end{aligned}$$

(44)

For a small pore in a wide panel, i.e. $w\gg h$, the integral term in Eq. (44) becomes insignificant, i.e.

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{b}-\frac{h}{\delta ^{2}w}M_{1}. \end{aligned}$$

(45)

1.1 A Panel with a Crack

Consider the path $M_{1}$ along a crack in an anti-clockwise direction for a crack that is placed perpendicular to the loading direction as shown in Fig. 14a. The crack path follows along the surfaces and encircling the crack tips to avoid the stress singularities present at the crack tips. According to (Budiansky and Rice 1970) the value of the M-integral is related to the crack tip driving force G as

$$\begin{aligned} M_{1}=bG. \end{aligned}$$

(46)

For a small crack G is given by the relation

$$\begin{aligned} G=\frac{K_{\text {I}}^{2}}{E_\mathrm{b}}=\frac{\pi }{2}\frac{\sigma _\mathrm{o}^{2}b}{E_\mathrm{b}}\,, \end{aligned}$$

(47)

where $K_{\text {I}}=\sigma _\mathrm{o}\sqrt{\pi b/2}$ is the stress intensity factor.

With this inserted in Eq. (45)

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{b}\left( 1-\frac{\pi }{2}\frac{b^{2}}{hw}\right) \ . \end{aligned}$$

(48)

By comparing with Eq. (25), the shape factor ${\tilde{\theta }}_\mathrm{E}$ for a crack is identified as

$$\begin{aligned} {\tilde{\theta }}_\mathrm{E}=\frac{\pi }{2}. \end{aligned}$$

(49)

1.2 A Panel with a Hole

A closed loop encircling a circular hole in a panel also in an anti-clockwise direction is displayed in Fig. 14b. Calculation of $M_{1}$ requires the stresses and strains on the perimeter of the hole. Absent tractions, i.e. $T_\mathrm{r}=T_{\phi }=0$ reduces the strain energy density to $W=\sigma _{\phi }^{2}/2E_\mathrm{b}$, whereas the only non-zero stress component is $\sigma _{\phi }$. With $n_{1}=\cos \phi , n_{2}=\sin \phi , x_{1}=\frac{b}{2}\cos \phi , x_{2}=\frac{b}{2}\sin \phi$, and $\text {d}{\varGamma }=\frac{b}{2}\text {d}\theta , M_{1}$ becomes

$$\begin{aligned} M_{1}=\int _{0}^{2\pi }\frac{\sigma _{\phi }^{2}}{4E_\mathrm{b}}b\text {d}\phi . \end{aligned}$$

(50)

The stress $\sigma _{\phi }$ may be found in text books on elastostatics, see e.g. (Fung 1965). The stress distribution is provided as

$$\begin{aligned} \sigma _{\phi }=\sigma _\mathrm{o}(1-2\cos 2\phi ). \end{aligned}$$

(51)

Inserting this into Eq. (50) one obtains

$$\begin{aligned} M_{1}=\frac{\sigma _\mathrm{o}^{2}b^{2}}{8E_\mathrm{b}}\int _{0}^{2\pi }(1-2\cos 2\phi )^{2}\text {d}\phi =\frac{3\pi }{4}\frac{\sigma _\mathrm{o}^{2}b^{2}}{E_\mathrm{b}}\,, \end{aligned}$$

(52)

after using the relations $r^{2}=x_{1}^{2}+x_{2}^{2}=b^{2}/4$ and $\text {d}{\varGamma }=r\text {d}\phi$. Inserted in Eq. (45) the result now reads

$$\begin{aligned} E_\mathrm{e}=E_\mathrm{b}\left( 1-\frac{3\pi }{4}\frac{b^{2}}{hw}\right) . \end{aligned}$$

(53)

The ${\tilde{\theta }}_\mathrm{E}$ for a circular hole is identified using Eq. (25) as

$$\begin{aligned} {\tilde{\theta }}_\mathrm{E}=\frac{3\pi }{4}. \end{aligned}$$

(54)