1 Introduction

The phenomenon of convective flow is prevalent in fields of physics and engineering, such as geothermal reservoirs (Jue 2002), float glass production (Prieto et al. 2002), flow and heat transfer in solar ponds (Mansour et al. 2004), air conditioning in rooms (Al-Sanea et al. 2012), cooling of electronic devices (Alves and Altemani 2012; Kuznetsov and Sheremet 2008), etc. Natural convection in a porous cavity has received considerable attention in recent years because of its relation to the thermal performance of many engineering installations (Nield and Bejan 2013). Natural convection heat transfer in domains containing superposed fluid and porous medium is a fundamental transport mechanism encountered in a wide range of engineering, geophysics, and scientific applications, such as packed bed solar energy storage, fibrous and granular insulation systems, water reservoirs, post-accident cooling of nuclear reactors, etc. (Bagchi and Kulacki 2014). Although buoyant convection in this system was first studied about 40 years ago, there has lately been renewed interest in convective flow in porous cavities owing to its importance in environmental and energy management problems in current scientific and geo-political context (Bagchi and Kulacki 2014). Application of systems and control concept of flow through porous media to oil and gas reservoir simulation and other application areas of subsurface flow simulation such as \(\mathrm{CO}_{2}\) storage, geothermal energy, or groundwater remediation are also important research topics in porous media nowadays (Jansen 2013).

It seems that there are only several studies in the literature on natural convection in cavities filled with viscous fluid with periodic temperature conditions imposed upon the bottom or sidewalls. For example, Poulikakos (1985) studied an enclosure with its left sidewall differentially heated, one half of the wall is heated and the other half is cooled, and the remaining walls are insulated. He showed that a penetrating thermal layer is formed, the size of which is a function of Rayleigh number and aspect ratio of the enclosure. Lage and Bejan (1993) studied enclosures with one sidewall heated using a pulsating heat flux and the other sidewall cooled at constant temperature. They showed that at high Rayleigh numbers, the buoyancy-driven flow has the tendency to resonate to the periodic heating that has been supplied from the side. Bilgen et al. (1995) used a system of discrete temperature sources placed periodically on the bottom wall of a shallow channel. Sarris et al. (2002) studied natural convection in a two-dimensional enclosure with sinusoidal upper wall temperature. The work by these authors was motivated by the need to understand the heat transfer characteristics in glass melting tanks, where a number of burners placed above the glass tank create periodic temperature profiles on the surface of the glass melt (Sarris et al. 1999).

A major area of recent investigation has been the reconciliation of the several mathematical nanofluid models currently in use. Of particular interest are the boundary conditions at the walls of the porous cavity and the prediction of the heat transfer coefficients when the convective currents are driven by sinusoidal temperature distributions. The main objective of the present study is, therefore, to analyze the natural convection in a square porous cavity with sinusoidal temperature distributions on both sidewalls filled with a nanofluid using the nanofluid mathematical model proposed by Buongiorno (2006). To the best of our knowledge, this problem has not been considered before, so that the reported results are new and original.

2 Basic Equations

Consider the free convection in a square porous cavity filled with a nanofluid based on water and nanoparticles. It is assumed that nanoparticles are suspended in the nanofluid using either surfactant or surface charge technology. This prevents nanoparticles from agglomeration and deposition on the porous matrix (Kuznetsov and Nield 2013; Nield and Kuznetsov 2014). Further, it is very important to explain how nanofluid flow is possible in a porous medium. It has been shown by Wu et al. (2010, 2011) that the porous matrix works as a filter for nanoparticles. This demonstrates that we are simulating here a real physics problem of natural convection in a square porous cavity filled with a nanofluid using the mathematical nanofluid model proposed by Buongiorno (2006) as in many papers pioneered by Nield and Kuznetsov (2009a, b, 2010, 2011, 2014) and Kuznetsov and Nield (2010a, b, c, d, 2011a, b, c, 2013).

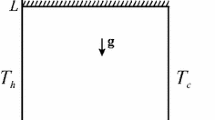
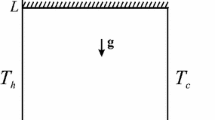
A schematic geometry of the problem under investigation is shown in Fig. 1, where \(\overline{{x}}\) and \(\overline{{y}}\) are the Cartesian coordinates and L is the size of the walls. The cavity is assumed to be impermeable, and the horizontal walls are assumed to be thermally insulated. At the same time, the vertical walls have imposed two sinusoidally varying temperature distributions according to the space coordinate as follows (Sarris et al. 2002; Deng and Chang 2008):

$$\begin{aligned} T({\overline{{y}}})&= T_\mathrm{c}+A_\mathrm{l}\sin \left( {\frac{2\uppi \overline{{y}}}{L}}\right) \quad \mathrm{at}\,\,\overline{{x}}=0,\end{aligned}$$
(1)
$$\begin{aligned} T({\overline{{y}}})&= T_\mathrm{c} +A_\mathrm{r}\sin \left( {\frac{2\uppi \overline{{y}}}{L}+\varphi }\right) \quad \mathrm{at}\;\overline{{x}}=L, \end{aligned}$$
(2)

where the reference temperatures of the sinusoidal temperature profiles on the left and right sidewalls are the same \(T_\mathrm{c},\) but the amplitude and phase of the sinusoidal profiles are, respectively, \(A_\mathrm{l}\) and 0, and \(A_\mathrm{r}\) and \(\varphi .\)

Fig. 1
figure 1

Physical model and coordinate system

Full size image

The Darcy–Boussinesq approximation is employed. Homogeneity and local thermal equilibrium in the porous medium is assumed. We consider a medium whose porosity is denoted by \(\varepsilon \) and permeability by K. The following are the four field equations for embody the conservation of total mass, momentum, thermal energy, and nanoparticles, respectively (see Buongiorno 2006; Kuznetsov and Nield 2013; Nield and Kuznetsov 2014):

$$\begin{aligned}&\nabla \cdot \mathbf{V}=0,\end{aligned}$$
(3)
$$\begin{aligned}&0=-\nabla p-\frac{\mu }{K}\mathbf{V}+\left[ {C\rho _\mathrm{p}+({1-C})\rho _{\mathrm{f}0}\left( {1- \beta \left( {T-T_\mathrm{c}}\right) }\right) } \right] \mathbf{g},\end{aligned}$$
(4)
$$\begin{aligned}&\sigma \frac{\partial T}{\partial t}+({\mathbf{V}\cdot \nabla })T=\alpha _\mathrm{m}\nabla ^{2}T+\delta \left[ {D_\mathrm{B} \nabla C\cdot \nabla T+\left( {{D_\mathrm{T}}/{T_\mathrm{c}}}\right) \nabla T\cdot \nabla T}\right] ,\end{aligned}$$
(5)
$$\begin{aligned}&\rho _\mathrm{p}\left( {\frac{\partial C}{\partial t}+\frac{1}{\varepsilon }({\mathbf{V}\cdot \nabla } ) C} \right) =-\nabla \cdot \mathbf{j}_\mathrm{p}, \end{aligned}$$
(6)

where V is the Darcy velocity vector; T is the fluid temperature; C is the nanoparticle volume fraction; t is the time; p is the fluid pressure; g is the gravity vector; \(D_\mathrm{B}\) is the Brownian diffusion coefficient; \(D_\mathrm{T}\) is the thermophoretic diffusion coefficient; \(\mathbf{j}_{p}=-\rho _\mathrm{p}[{D_\mathrm{B} \nabla C+({{D_\mathrm{T}}/{T_\mathrm{c}}}) \nabla T}]\) is the nanoparticles mass flux; \(\rho _{\mathrm{f}0}\) is the reference density of the fluid; \(\alpha _\mathrm{m},\;\mu \), and \(\rho _\mathrm{p}\) denote the effective thermal diffusivity of the porous medium, the dynamic viscosity, and nanoparticle mass density, respectively; \(\delta \) and \(\sigma \) are quantities defined by \(\delta =\varepsilon (\rho C_\mathrm{p})_\mathrm{p}/(\rho C_\mathrm{p})_\mathrm{f}\) and \(\sigma =(\rho C_\mathrm{p})_\mathrm{m}/(\rho C_\mathrm{p})_\mathrm{f};\,C_\mathrm{p}\) is the heat capacity at constant pressure; \((\rho C_\mathrm{p})_\mathrm{f}\) is heat capacity of the base fluid; \((\rho C_\mathrm{p})_\mathrm{p}\) is effective heat capacity of the nanoparticle material; \((\rho C_\mathrm{p})_\mathrm{m}\) is effective heat capacity of the porous medium; and \(\beta \) is the coefficient of thermal expansion.

The flow is assumed to be slow so that an advective term and a Forchheimer quadratic term do not appear in the momentum equation. In keeping with the Boussinesq approximation and an assumption that the nanoparticle concentration is dilute, and with a suitable choice for the reference pressure, we can linearize the momentum equation and write Eq. (4) as

$$\begin{aligned} 0=-\nabla p-\frac{\mu }{K}\mathbf{V}+\left[ {C\left( {\rho _\mathrm{p}-\rho _{\mathrm{f}0}}\right) +\rho _{\mathrm{f}0}\left( {1-\beta \left( {T-T_\mathrm{c}}\right) \left( {1-C_{0}}\right) }\right) }\right] \mathbf{g}. \end{aligned}$$
(7)

Equations (3), (5)–(7) for the problem under consideration can be written, after the pressure p is eliminated by cross-differentiation, in Cartesian coordinates \(\overline{{x}}\) and \(\overline{{y}}\) as

$$\begin{aligned}&\frac{\partial u}{\partial \overline{{x}}}+\frac{\partial v}{\partial \overline{{y}}}=0,\end{aligned}$$
(8)
$$\begin{aligned}&0=-\frac{\mu }{K}\left( {\frac{\partial u}{\partial \overline{{y}}}-\frac{\partial v}{\partial \overline{{x}}}} \right) +g\left( {\rho _\mathrm{p} -\rho _{\mathrm{f}0} } \right) \frac{\partial C}{\partial \overline{{x}}}-\left( {1-C_{0}} \right) \rho _{\mathrm{f}0} \beta g \frac{\partial T}{\partial \overline{{x}}},\end{aligned}$$
(9)
$$\begin{aligned}&\sigma \frac{\partial T}{\partial t}+u\frac{\partial T}{\partial \overline{{x}}}+v\frac{\partial T}{\partial \overline{{y}}}=\alpha _\mathrm{m} \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) +\delta \left\{ {D_\mathrm{B} \left( {\frac{\partial C}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{x}}}+\frac{\partial C}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{y}}}} \right) } \right. \nonumber \\&\qquad \quad +\left( {\frac{D_\mathrm{T}}{T_\mathrm{c}}}\right) \left. {\left[ {\left( {\frac{\partial T}{\partial \overline{{x}}}}\right) ^{2}+\left( {\frac{\partial T}{\partial \overline{{y}}}} \right) ^{2}} \right] }\right\} ,\end{aligned}$$
(10)
$$\begin{aligned}&\frac{\partial C}{\partial t}+\frac{1}{\varepsilon } \left( {u\frac{\partial C}{\partial \overline{{x}}}+v\frac{\partial C}{\partial \overline{{y}}}} \right) =D_\mathrm{B} \left( {\frac{\partial ^{2}C}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}C}{\partial \overline{{y}}^{2}}} \right) +\left( {\frac{D_\mathrm{T}}{T_\mathrm{c}}}\right) \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) , \end{aligned}$$
(11)

where u and v are the velocity components along \(\overline{{x}}\) and \(\overline{{y}}\) directions, respectively.

One can introduce a stream function \(\overline{{\psi }}\) defined by

$$\begin{aligned} u=\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}},\quad v=- \frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}, \end{aligned}$$
(12)

so that Eq. (8) is satisfied identically. We are then left with the following equations taking into account steady-state regime:

$$\begin{aligned} \frac{\partial ^{2}\overline{{\psi }}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{\psi }}}{\partial \overline{{y}}^{2}}&= -\frac{({1-C_{0}})\rho _{\mathrm{f}0}gK\beta }{\mu }\frac{\partial T}{\partial \overline{{x}}}+\frac{\rho _\mathrm{p}-\rho _{\mathrm{f}0} }{\mu }gK\frac{\partial C}{\partial \overline{{x}}},\end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{x}}}-\frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{y}}}&= \alpha _\mathrm{m}\left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) +\delta \left\{ D_\mathrm{B} \left( {\frac{\partial C}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{x}}}+\frac{\partial C}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{y}}}} \right) \right. \nonumber \\&\qquad \left. +\frac{D_\mathrm{T}}{T_\mathrm{c}}\left[ {\left( {\frac{\partial T}{\partial \overline{{x}}}} \right) ^{2}+\left( {\frac{\partial T}{\partial \overline{{y}}}} \right) ^{2}} \right] \right\} ,\end{aligned}$$
(14)
$$\begin{aligned} \frac{1}{\varepsilon }\left( {\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial C}{\partial \overline{{x}}}-\frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial C}{\partial \overline{{y}}}} \right)&= D_\mathrm{B}\left( {\frac{\partial ^{2}C}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}C}{\partial \overline{{y}}^{2}}} \right) +\frac{D_\mathrm{T}}{T_\mathrm{c}}\left[ {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right] . \end{aligned}$$
(15)

Introducing the following dimensionless variables

$$\begin{aligned} x={\overline{{x}}}/L,\quad y={\overline{{y}}}/L,\quad \psi ={\overline{{\psi }}}/{\alpha _\mathrm{m}},\quad \theta ={\left( {T-T_\mathrm{c}} \right) }/{\Delta T},\quad \phi =C/{C_{0}}, \end{aligned}$$
(16)

where \(\Delta T=A_\mathrm{l}\) (amplitude of the sinusoidal profile), and substituting (16) into Eqs. (13)–(15), we obtain

$$\begin{aligned} \frac{\partial ^{2}\psi }{\partial x^{2}}+\frac{\partial ^{2}\psi }{\partial y^{2}}&= -Ra\frac{\partial \theta }{\partial x}+Ra\cdot \mathrm{Nr}\frac{\partial \phi }{\partial x},\end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}&= \frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}+\mathrm{Nb} \left( {\frac{\partial \phi }{\partial x}\frac{\partial \theta }{\partial x}+\frac{\partial \phi }{\partial y}\frac{\partial \theta }{\partial y}} \right) +\mathrm{Nt} \left[ {\left( {\frac{\partial \theta }{\partial x}} \right) ^{2}+\left( {\frac{\partial \theta }{\partial y}} \right) ^{2}} \right] ,\nonumber \\\end{aligned}$$
(18)
$$\begin{aligned} \frac{\partial \psi }{\partial y}\frac{\partial \phi }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \phi }{\partial y}&= \frac{1}{Le}\left[ {\frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}} \right] +\frac{1}{Le} \frac{\mathrm {Nt}}{\mathrm {Nb}} \left[ {\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}}\right] , \end{aligned}$$
(19)

where \(Ra={({1-C_{0}})gK\rho _{\mathrm{f}0} \beta \Delta TL}/{({\alpha _\mathrm{m} \mu })}\) is the Rayleigh number. The corresponding boundary conditions of these equations are given by

$$\begin{aligned}&\psi =0,\quad \theta =\sin (2\uppi y),\quad {\widetilde{\mathbf{j}}}_\mathrm{p}=0\quad \left( \mathrm{or}\;\mathrm{Nb}\frac{\partial \phi }{\partial x}+\mathrm{Nt} \frac{\partial \theta }{\partial x}=0 \right) \quad \mathrm{on}\; x=0, \nonumber \\&\psi =0,\quad \theta =\gamma \sin (2 \uppi y+\varphi ),\quad {\widetilde{\mathbf{j}}}_\mathrm{p}=0\quad \left( \mathrm{or}\;\mathrm{Nb} \frac{\partial \phi }{\partial x}+\mathrm{Nt} \frac{\partial \theta }{\partial x}=0 \right) \quad \mathrm{on}\quad x=1, \nonumber \\&\psi =0,\quad \frac{\partial \theta }{\partial y}=0,\quad \frac{\partial \phi }{\partial y}=0\quad \mathrm{on}\quad y=0\quad \mathrm{and}\quad y=1, \end{aligned}$$
(20)

where \({\tilde{\mathbf{j}}}_\mathrm{p}\) is the dimensionless nanoparticle flux. Here, the five parameters Nr, Nb, Nt, Le, and \(\gamma \) denote a buoyancy-ratio parameter, a Brownian motion parameter, a thermophoresis parameter, a Lewis number, and an amplitude ratio of the sinusoidal temperature on the right side wall to that on the left side wall, respectively, which are defined as

$$\begin{aligned} \mathrm{Nr}=\frac{({\rho _\mathrm{p} -\rho _{\mathrm{f}0} })C_{0} }{ \rho _{\mathrm{f}0} \beta \Delta T({1-C_{0} })},\quad \mathrm{Nb}=\frac{ \delta D_\mathrm{B} C_{0} }{\alpha _\mathrm{m}},\quad \mathrm{Nt}=\frac{\delta D_\mathrm{T} \Delta T}{\alpha _\mathrm{m} T_\mathrm{c}},\quad Le=\frac{\alpha _\mathrm{m}}{\varepsilon D_\mathrm{B}},\quad \gamma =\frac{A_\mathrm{r} }{A_\mathrm{l} }.\nonumber \\ \end{aligned}$$
(21)

It should be noticed that for Nr = Nb = Nt = 0 (regular fluid), Eqs. (17) and (18) reduce to those of Walker and Homsy (1978), Bejan (1979), Beckermann et al. (1986), Gross et al. (1986), Moya et al. (1987), Manole and Lage (1992), and Baytas and Pop (1999).

The physical quantities of interest are the local Nusselt number Nu, the local Sherwood number Sh, and the average Nusselt \(\overline{Nu}\) and Sherwood \(\overline{Sh}\) numbers.

The local Nusselt and Sherwood numbers are defined as

$$\begin{aligned} Nu_\mathrm{l} \!=\!-\left( {\frac{\partial \theta }{\partial x}} \right) _{x=0},\quad Sh_\mathrm{l} \!=\!-\left( {\frac{\partial \phi }{\partial x}}\right) _{x=0},\quad Nu_\mathrm{r} \!=\!-\left( {\frac{\partial \theta }{\partial x}} \right) _{x=1},\quad Sh_\mathrm{r}\!=\!-\left( {\frac{\partial \phi }{\partial x}} \right) _{x=1}.\nonumber \\ \end{aligned}$$
(22)

The average Nusselt and Sherwood numbers are defined as

$$\begin{aligned} \overline{Nu} _\mathrm{l} =\int \limits _{0}^{1} {Nu_\mathrm{l}}\mathrm{d}y,\quad \overline{Sh} _\mathrm{l} =\int \limits _{0}^{1} {Sh_\mathrm{l} \mathrm{d}y},\quad \overline{Nu} _\mathrm{r} =\int \limits _{0}^{1}{Nu_\mathrm{r}} \mathrm{d}y,\quad \overline{Sh} _\mathrm{r} =\int \limits _{0}^{1} {Sh_\mathrm{r} \mathrm{d}y}. \end{aligned}$$
(23)

It should be noted here that for an analysis of Sherwood numbers it is possible to study only Nusselt numbers because at the left and right vertical walls we have \(\frac{\partial \phi }{\partial x}=-\frac{\mathrm{Nt}}{\mathrm{Nb}}\frac{\partial \theta }{\partial x}\) taking into account boundary conditions for \(\phi \) (Eqs. 20). Therefore, the further analysis concerning integral parameters will be about only average Nusselt number because \(Sh=-\frac{\mathrm {Nt}}{\mathrm {Nb}}Nu\) and \(\overline{Sh} =-\frac{\mathrm {Nt}}{\mathrm {Nb}}\overline{Nu}.\)

3 Numerical Method

The partial differential equations (17)–(19) with corresponding boundary conditions (20) were solved using the finite-difference method (see Aleshkova and Sheremet 2010; Sheremet and Trifonova 2013; Sheremet et al. 2014). The steady-state solution was obtained like the time limit for solution of the transient problem, where the approximation of the convective terms was conducted by the difference scheme of second order, allowing to consider a sign of velocity, and the approximation of the diffusion terms was conducted by the central differences. The transient equations were solved on the basis of Samarskii locally one-dimensional scheme. The linear discretized equations were solved by Thomas algorithm. The Poisson equation for the stream function was discretized by means of the five-point difference scheme on the basis of central differences for the second derivatives. The obtained linear discretized equation was solved by the successive over-relaxation method. Optimum value of the relaxation parameter was chosen on the basis of computing experiments. The computation is terminated when the residuals for the stream function get below \(10^{-7}.\)

The present models, in the form of an in-house computational fluid dynamics code, have been validated successfully against the works of Walker and Homsy (1978), Bejan (1979), Beckermann et al. (1986), Gross et al. (1986), Moya et al. (1987), Manole and Lage (1992), and Baytas and Pop (1999) for the steady-state natural convection in a square porous cavity with isothermal vertical and adiabatic horizontal walls. Table 1 shows the values of the average Nusselt number computed for various Rayleigh numbers in the range of 10–\(10^{4}\) in comparison with other authors.

Table 1 Comparison of the average Nusselt number of the hot wall
Full size table

The performance of sinusoidal heating part of the model was tested against the results of Deng and Chang (2008) and Sivasankaran and Bhuvaneswari (2013) for steady-state natural convection in a square cavity with sinusoidal heating at vertical walls filled with the regular fluid [see Eqs. (17)–(20) where Nr = Nb = Nt = 0] for Rayleigh numbers \(10^{3},\,10^{4}\), and \(10^{5},\) for Prandtl number 0.7 and for the amplitude ratio of the sinusoidal temperature on the right side wall to that on the left side wall 1.0. Figures 2, 3 and 4 show a good agreement between the obtained streamlines and isotherms for different Rayleigh numbers and the numerical results of Deng and Chang (2008), and Sivasankaran and Bhuvaneswari (2013).

Fig. 2
figure 2

Comparison of streamlines \(\varPsi \) and isotherms \(\varTheta \) at \(Ra=10^{3},\, \varphi =0:\) numerical data of Deng and Chang (2008) (a), numerical data of Sivasankaran and Bhuvaneswari (2013) (b), and present results (c)

Full size image
Fig. 3
figure 3

Comparison of streamlines \(\varPsi \) and isotherms \(\varTheta \) at \(Ra=10^{4},\,\varphi =0:\) numerical data of Deng and Chang (2008) (a), and present results (b)

Full size image
Fig. 4
figure 4

Comparison of streamlines \(\varPsi \) and isotherms \(\varTheta \) at \(Ra=10^{5},\, \varphi =\uppi /2:\) numerical data of Deng and Chang (2008) (a), numerical data of Sivasankaran and Bhuvaneswari (2013) (b), and present results (c)

Full size image

For the purpose of obtaining grid-independent solution, a grid sensitivity analysis is performed. The grid-independent solution was performed by preparing the solution for steady-state natural convection in a square porous cavity with sinusoidal temperature distributions on vertical walls filled with a nanofluid at \(Ra=100,\,\mathrm{Nr}=\mathrm{Nb}=\mathrm{Nt}=0.1,\,Le=10,\,\gamma =1,\, \varphi =0.\) Six cases of a uniform grid are tested: \(100\times 100,\,200\times 200,\,300\times 300,\,400\times 400,\,500\times 500\), and \(600\times 600\). Table 2 shows an effect of the mesh on the average Nusselt number of the left vertical wall.

Table 2 Variations of the average Nusselt numbers of the left vertical wall with the uniform grid
Full size table

On the basis of the conducted verifications, the uniform grid of \(500\times 500\) points has been selected for the following analysis.

4 Results and Discussion

Numerical investigations of the boundary value problem (17)–(20) have been carried out at the following values of key parameters: Rayleigh number (Ra = 100), Lewis number (Le = 10–1,000), the buoyancy-ratio parameter (Nr = 0.1–0.4), the Brownian motion parameter (Nb = 0.1–0.4), the thermophoresis parameter (Nt = 0.1–0.4), the amplitude ratio of the sinusoidal temperature on the right side wall to that on the left side wall \((\gamma =0\)–1), and the phase deviation \((\varphi =0\)–\(\uppi \)). Particular efforts have been focused on the effects of these parameters on the fluid flow, heat and mass transfer characteristics.

Figure 5 illustrates streamlines, isotherms, and isoconcentrations at different values of the Lewis number at Nr = Nb = Nt = 0.1, \(\gamma =1\), and \(\varphi =0.\)

Fig. 5
figure 5

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for Nr = Nb = Nt = 0.1, \(\gamma =1,\,\varphi =0:\,Le=10\) (a), \(Le=100\) (b), and \(Le=1,000\) (c)

Full size image

Regardless of the Lewis number value, four convective cells are formed inside the cavity. Two convective cells are clockwise vortices that are located in the left bottom part and right top part of the cavity, and two convective cells are counter clockwise vortices that are located in the right bottom part and left top part of the cavity. The main reason for an appearance of these circulations is an effect of vertical walls with sinusoidally varying temperature distributions. It should be noted that an intensity of two convective cells in the top part of the cavity is greater than an intensity of two convective cells in the bottom part of the cavity that can be explained by an effect of the buoyancy force. These four vortices are separated by virtual vertical and horizontal walls which are both impervious and adiabatic.

Convective cells cores are close to the vertical walls due to large temperature differences in these zones. An increase in the Lewis number does not change the intensity and configuration of the convective cells and isotherms. Temperature and stream function distributions are symmetrical with respect to vertical line x = 0.5. Regardless of the Lewis number value, the heat conduction is a dominated heat transfer in the domain of interest.

The main variations with the Lewis number are related to the isoconcentrations. These fields characterize the distributions of the nanoparticles volume fraction inside the square cavity. Regardless of the Lewis number value, the considered regime is defined by an increase in \(\phi \) in the top part of the cavity and a decrease in \(\phi \) in the bottom part of the cavity. At small values of \(Le\le 10\), the distribution of nanoparticles is non-homogeneous taking into account Fig. 5. Such description of this regime is due to an essential deviation of the nanoparticles volume fraction from the average value \(\phi =1.\) Moreover, the heat conduction regime enhances the effect of the thermophoresis phenomenon, and therefore nanoparticles distribution is non-homogeneous with decrease in \(Le\le 10.\) At Le = 1,000 (Fig.  5c) when the concentration boundary layer is very thin, the distribution of nanoparticles is homogeneous. An increase in Le leads to homogeneity of distribution of the nanoparticles volume fraction inside the considered cavity. It physically means that flow with large Lewis number (e.g., the nanofluid with nanoparticles of 1–100 nm diameter) prevents spreading nanoparticles in the nanofluid. Therefore, we have large homogeneous areas in the domains of convective cells where the non-homogeneous areas become more confined close to the boundaries, vertical and horizontal middle sections.

An effect of the dimensionless time and Lewis number on the average Nusselt number at left vertical wall is presented in Fig. 6. An increase in Le from 10 to 1,000 leads to an insignificant decrease in \(\overline{Nu_\mathrm{l}}.\) Taking into account boundary conditions for the nanoparticles volume fraction (20), distributions of \(\overline{Sh_\mathrm{l}}\) are similar to distributions of \(\overline{Nu_\mathrm{l}}.\)

Fig. 6
figure 6

Variation of the average Nusselt number at left vertical wall with the Lewis number and dimensionless time for Nr = Nb = Nt = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image

Figures 5b and 7 illustrate streamlines, isotherms, and isoconcentrations at different values of the buoyancy-ratio parameter (Nr = 0.1 and 0.4). An increase in Nr does not lead to changes in all local fields of stream function, temperature, and nanoparticles volume fraction inside the cavity for considered values of key parameters. It is worth noting, here, that an increase in the buoyancy-ratio parameter leads to insignificant increase in \(\overline{Nu_\mathrm{l}}\) and \(\overline{Sh_\mathrm{l}}\) (Fig. 8).

Fig. 7
figure 7

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for \(Le=100,\) Nr = 0.4, Nb = Nt = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image
Fig. 8
figure 8

Variation of the average Nusselt number at left vertical wall with the buoyancy-ratio parameter and dimensionless time for \(Le=100,\) Nb = Nt = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image

Figures 5b and 9 illustrate streamlines, isotherms, and isoconcentrations at different values of the Brownian motion parameter (Nb = 0.1 and 0.4). It can be seen from these figures that an increase in the Brownian motion parameter Nb leads to both significant changes in isoconcentrations (reduction of the concentration boundary layer thickness) and conservation of streamlines and isotherms. Changes in isoconcentrations are related to very small increase in \(\phi \) in the upper part of the cavity and very small decrease in \(\phi \) in the bottom part of the cavity. Taking into account such variations of \(\phi \), it is possible to conclude that an increment in Nb leads to homogeneity of distribution of the nanoparticles volume fraction inside the considered cavity, because Fig. 9 displays a deviation less than 1 % from the average value \(\phi =1\) relative to the case of Nb = 0.1 shown in Fig. 5b. Modification of isoconcentrations due to an increase in the Brownian motion parameter leads to an unessential decrease in the average Nusselt number (Fig. 10).

Fig. 9
figure 9

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for \(Le=100,\) Nb = 0.4, Nr = Nt = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image
Fig. 10
figure 10

Variation of the average Nusselt number at left vertical wall with the Brownian motion parameter and dimensionless time for \(Le=100,\) Nr = Nt = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image

Figures 5b and 11 illustrate streamlines, isotherms, and isoconcentrations at different values of the thermophoresis parameter. An increase in Nt leads to changes in all characteristics (streamlines, isotherms, and isoconcentrations) that can be described in the following way. One can find an intensification and increase in sizes of two convective cells in the upper part of the cavity \(|\psi |_{\max ,\mathrm{upper\;part}}^{\mathrm{Nt}=0.1}=2.64<|\psi |_{\max ,\mathrm{upper\; part}}^{\mathrm{Nt}=0.4} =2.94\) and an attenuation and decrease in sizes of two convective cells in the bottom part of the cavity \(|\psi |_{\max ,\mathrm{bottom\;part}}^{\mathrm{Nt}=0.1} =2.43>|\psi |_{\max ,\mathrm{bottom\; part}}^{\mathrm{Nt}=0.4} =2.11.\) Therefore, with Nt the difference between the maximum and minimum value of the stream functions also increases indicating higher values of local velocity. At the same time, an increase in the thermophoresis parameter leads to more intensive heating of the bottom part and less intensive cooling of the upper part of the enclosure in comparison with the case Nt = 0.1 shown in Fig. 5b. Such changes characterize a decrease in the temperature differences in the bottom part and an increase in the temperature differences in the upper part that leads to changes of convective cells intensity as has been mentioned above.

Fig. 11
figure 11

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for \(Le=100,\) Nt = 0.4, Nr = Nb = 0.1, \(\gamma =1,\,\varphi =0\)

Full size image

It should be noted that the main variations with the thermophoresis parameter are related to the isoconcentrations. An increase in Nt leads to essential changes of the nanoparticles volume fraction both in the upper and bottom parts of the cavity. In general, these distributions of \(\phi \) can be considered as non-homogeneous.

An effect of the dimensionless time and thermophoresis parameter on the average Nusselt number at left vertical wall is depicted in Fig. 12. It is necessary to note that an increase in Nt leads to an increase in the average Nusselt number and, accordingly, in the average Sherwood number taking into account boundary conditions (20).

Fig. 12
figure 12

Variation of the average Nusselt number at left vertical wall with the thermophoresis parameter and dimensionless time for \(Le=100,\) Nr = Nb = 0.1, \(\gamma =1,\, \varphi =0\)

Full size image

Figures 5b and 13 illustrate streamlines, isotherms, and isoconcentrations at different values of the amplitude ratio of the sinusoidal temperature on the right side wall to that on the left side wall. At \(\gamma =0\) (Fig. 13a) when the temperature at the right vertical wall equals zero, two horizontal convective cells are formed inside the square cavity. An appearance of these vortices can be explained by an effect of periodic temperature conditions imposed upon the left vertical wall. At this regime, one can find an influence of convective heat transfer mechanism on velocity and temperature fields that lead to small distortion of isotherm \(\theta =0\) close to the right wall. It should be noted that an intensity of the top convective cell is greater than an intensity of the bottom one \(|\psi |_{\max }^{\mathrm{top\;cell}} =2.8>|\psi |_{\max }^{\mathrm{bottom\;cell}} =2.64\) that can be explained by more intensive heating of the bottom part of the cavity.

Isoconcentrations reflect an increase in the nanoparticles volume fraction up to 3 % from the average value \(\phi =1\) in the upper part of the cavity and similar decrease in the nanoparticles volume fraction in the bottom part of the cavity. Such field characterizes a less homogeneous distribution of nanoparticles.

An increase in the amplitude ratio up to \(\gamma =0.25\) (Fig. 13b), which characterizes a presence of small periodic temperature at the right vertical wall, leads to a formation of extra weak convective cells close to this side wall. It should be noted here that the right upper convective cell starts to join to the left bottom convective cell. Such behavior leads to small deformation of the left upper convective cell. Isotherms reflect a formation of both a heat source at the bottom part and a heat sink at the top part of the right vertical wall. An appearance of such heat elements leads to a formation of additional less homogeneous areas close to these elements. Further increase in \(\gamma \) leads to both an intensification of the right top and bottom convective cells and an expansion of less homogeneous areas close to the heat sink and heat source.

Fig. 13
figure 13

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for \(Le=100,\) Nr = Nb = Nt = 0.1, \(\varphi =0:\,\gamma =0\) (a), \(\gamma =0.25\) (b), \(\gamma =0.5\) (c), and \(\gamma =0.75\) (d)

Full size image

An effect of the dimensionless time and amplitude ratio on the average Nusselt number at left vertical wall is depicted in Fig. 14. It is necessary to note that an increase in \(\gamma \) leads to a decrease in the average Nusselt number and, accordingly, in the average Sherwood number taking into account boundary conditions (20). These changes can be explained by an interaction between thermal boundary layers and concentration boundary layers formed close to the vertical side walls having periodic temperature. Such interaction leads to a decrease in the temperature and concentration differences close to these walls owing to a reduction of convective cells and areas of temperature and concentration changes.

Fig. 14
figure 14

Variation of the average Nusselt number at left vertical wall with the amplitude ratio and dimensionless time for \(Le=100,\) Nr = Nb = Nt = 0.1, \(\varphi =0\)

Full size image

Figures 5b and 15 illustrate streamlines, isotherms, and isoconcentrations at different values of the phase deviation \(\varphi \) for Le = 100, Nr = Nb = Nt = 0.1, and \(\gamma =1.\) An increase in the phase deviation up to \(\uppi /4\) (Fig. 15a) leads to a combination of the left bottom convective cell and the right upper one. Such changes are caused by a decrease in sizes of the right bottom heat source. At the same time, isoconcentrations reflect convective cells where the distribution of the nanoparticles in the global vortex area is highly homogeneous. Less homogeneous areas are confined close to the heat sources and sinks on the vertical side walls, and also these zones propagate along borders between vortices in streamwise. An increase in \(\varphi \) up to \(\uppi /2\) (Fig. 15b) leads to an intensification of both clockwise vortex and counter clockwise vortex located in the upper part of the cavity. At the same time, one can find an attenuation of convective cell in the right bottom corner due to a decrease in size of the right bottom heat source.

Fig. 15
figure 15

Streamlines \(\psi ,\) isotherms \(\theta \), and isoconcentrations \(\phi \) for \(Le=100,\) Nr = Nb = Nt = 0.1, \(\gamma =1:\,\varphi =\uppi /4\) (a), \(\varphi =\uppi /2\) (b), \(\varphi =3\uppi /4\) (c), and \(\varphi =\uppi \) (d)

Full size image

Isoconcentrations characterize both a decrease in nanoparticles volume fraction in the upper part and an increase in \(\phi \) in the bottom part along the wall in comparison with the case \(\varphi =\uppi /4.\) Further increase in \(\varphi \) leads to an attenuation of the global bottom convective cell and an intensification of the upper one, and at \(\varphi =\uppi \) (Fig. 15d) one can find two horizontal vortices of equal intensity. Distributions of nanoparticles reflect structures of convective cells and characterize a formation of two large homogeneous areas.

An effect of the dimensionless time and phase deviation on the average Nusselt number at left vertical wall is depicted in Fig. 16. It should be noted here that an increase in \(\varphi \) leads to an increase in the average Nusselt number and, accordingly, in the average Sherwood number with formation of non-monotonic regions. An appearance of these increasing and decreasing zones characterizes a replacement of several velocity and temperature configurations before steady-state regime. Such behavior can be considered as unsteady regime.

Fig. 16
figure 16

Variation of the average Nusselt number at left vertical wall with the phase deviation and dimensionless time for \(Le=100,\) Nr = Nb = Nt = 0.1, \(\gamma =1\)

Full size image

5 Conclusions

The laminar natural convective flow and heat transfer of a water-based nanofluid in a square porous cavity having sinusoidal temperature distributions on both side walls have been numerically investigated using the nanofluid model proposed by Buongiorno. Mathematical model has been formulated in dimensionless stream function and temperature, and solved numerically on the basis of a second-order accurate finite-difference method.

The developed algorithm has been validated by direct comparisons with previously published papers, and the results have been found to be in good agreement. Distributions of streamlines, isotherms, and isoconcentrations at a wide range of key parameters have been obtained. Based on the findings in this study, we conclude that the average Nusselt and Sherwood numbers are increasing functions of the buoyancy-ratio parameter, thermophoresis parameter, and phase deviation, and decreasing functions of the Lewis number, Brownian motion parameter, and amplitude ratio. Low Lewis number and high thermophoresis parameter reflect essential non-homogeneous distribution of the nanoparticles inside the cavity. Therefore, for such range of Le and Nt, a non-homogeneous model is more appropriate for the description of the system.