Impact of Non-uniform Properties on Governing Equations for Fluid Flows in Porous Media

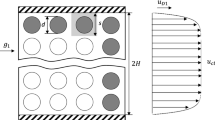
Abstract

The macroscopic governing equations of a compressible multicomponents flow with non-uniform viscosity and with mass withdrawal (due to heterogeneous reactions) in a porous medium are developed. The method of volume averaging was used to transform local (or microscopic) governing equations into averaged (or macroscopic) governing equations. The impacts of compressibility, non-uniform viscosity, and mass withdrawal on the form of the averaged equations and on the value of the macroscopic transport coefficients were investigated. The results showed that the averaged mass conservation equation is significantly affected by mass withdrawal when a specific criterion on the size of the domain is respected. The results also showed that the form of the averaged momentum equations is not affected by mass withdrawal, by compressibility effects or by non-uniform viscosity, provided that the Reynolds number at the pore level is small. Nonetheless, the velocity field is affected by the heterogeneous reaction via the averaged mass conservation equation, and also by viscosity variations due to the presence of the volume-averaged viscosity (which value changes with position) in the averaged momentum equations. A new closure variable definition was proposed to formulate the closure problem, which avoided the need to solve an integro-differential equation in the closure problem. This formulation was used to show that the permeability tensor only depends on the geometry of the porous medium. In other words, that tensor is independent on whether the fluid is compressible/incompressible, has uniform/non-uniform viscosities, and whether mass withdrawal due to heterogeneous reactions is present/absent.

Appendices

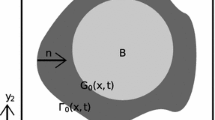
Appendix 1: Boundary Condition at $\Gamma _{\alpha \beta }$

In this Appendix, the boundary conditions associated to the fluid velocity ${\varvec{u}}$ is developed, the fluid being made of species $B=1,2,\ldots ,N$. In this paper, one of these species (the species $A)$ reacts at the surface $\Gamma _{\alpha \beta }$, which may be written as

$$\begin{aligned} {\varvec{n}}_{\alpha \beta } \cdot \rho _A {\varvec{u}}_A =\rho \textit{Ky}_A\;\;\;\; \hbox { at }\Gamma _{\alpha \beta }, \end{aligned}$$

(99)

where $\rho _A$ and ${\varvec{u}}_A$ are the density and velocity of species $A$, and other variables have been defined in the text. The other species do not react at the surface $\Gamma _{\alpha \beta }$, which yields

$$\begin{aligned} {\varvec{n}}_{\alpha \beta } \cdot \rho _B {\varvec{u}}_B =0\;\;\;\; \hbox { at } \Gamma _{\alpha \beta },\, \forall B\ne A. \end{aligned}$$

(100)

Notice that the species velocities ${\varvec{u}}_A$ or ${\varvec{u}}_B$ are defined as being the sum of the fluid velocity ${\varvec{u}}$ and of the diffusion velocity ${\varvec{{u}}}{^{\prime }}_A$ or ${\varvec{{u}}}{^{\prime }}_B$ (e.g., Eq. (12.154) in Kee et al. 2003; Eq. (12) in Whitaker 1999). In other words, they are expressed as ${\varvec{u}}_A ={\varvec{u}}+{\varvec{{u}}}{^{\prime }}_A$ and ${\varvec{u}}_B ={\varvec{u}}+{\varvec{{u}}}{^{\prime }}_B$. Hence, diffusional mass transfer at surface $\Gamma _{\alpha \beta }$ is implicitly taken into account by ${\varvec{u}}_A$ and ${\varvec{u}}_B$, in Eqs. (99) and (100). Summation of Eq. (99) with the $N-1$ boundary conditions given by Eq. (100) yields

$$\begin{aligned} \sum _{B=1}^N {{\varvec{n}}_{\alpha \beta } \cdot \rho _B {\varvec{u}}_B} =\rho \textit{Ky}_A \;\;\;\;\hbox { at } \Gamma _{\alpha \beta } \end{aligned}$$

(101)

or more concisely,

$$\begin{aligned} {\varvec{n}}_{\alpha \beta } \cdot {\varvec{u}}=\textit{Ky}_A\;\;\;\; \hbox { at }\Gamma _{\alpha \beta }, \end{aligned}$$

(102)

where the variable $\rho$ has been canceled out using the following definitions (Whitaker 2009):

$$\begin{aligned} \rho \equiv \sum _{B=1}^N {\rho _B} \;\;\;\;\;\; {\varvec{u}}\equiv \frac{1}{\rho }\sum _{B=1}^N \rho _B {\varvec{u}}_B. \end{aligned}$$

(103)

Hence, the normal component of the fluid velocity u at the surface $\Gamma _{\alpha \beta }$ is determined by Eq. (102). Finally, it is assumed that the no-slip condition is applied at the boundaries $\Gamma _{\alpha \beta }$. In other words, the tangential component of u is zero, so that the boundary condition for ${\varvec{u}}$ may finally be written as ${\varvec{u}}=\textit{Ky}_A {\varvec{n}}_{\alpha \beta }$ at $\Gamma _{\alpha \beta }$.

Appendix 2: Spatial Averaging Theorems

In this section, six different versions of the spatial averaging theorem are presented. To do so, we start with the fundamental spatial averaging theorem (Whitaker 1967) for a scalar field $a$, i.e.,

$$\begin{aligned} \frac{1}{V}\int \limits _{\Omega _\alpha } \nabla a\; {\text{ d }}V =\nabla \left( {\frac{1}{V}\int \limits _{\Omega _\alpha } a\; {\text{ d }}V} \right) +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {{\varvec{n}}_{\alpha \beta } a\; {\text{ d }}A}, \end{aligned}$$

(104)

which may be written in a more compact form as

1.1 Theorem 1

$$\begin{aligned} \left\langle {\nabla a} \right\rangle =\nabla \left\langle a \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {{\varvec{n}}_{\alpha \beta } a\; {\text{ d }}A}. \end{aligned}$$

(105)

This theorem is valid for representative elementary volumes (REV) of constant size and orientation. As one can see in Eq. (105), this theorem allows an interchange between the averaging operator and the gradient operator $\nabla$ applied to a scalar field $a$ in a porous medium.

To obtain an equivalent theorem for a vector field ${\varvec{a}}$, the expression $\left\langle {\nabla {\varvec{a}}} \right\rangle$ is multiplied by an arbitrary uniform vector ${\varvec{w}}$, which yields

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle \cdot {\varvec{w}}=\left\langle {\nabla \left( {{\varvec{a}}\cdot {\varvec{w}}} \right) }\right\rangle . \end{aligned}$$

(106)

The equality given in Eq. (106) may be demonstrated with tensor analysis. The expression $\left( {{\varvec{a}}\cdot {\varvec{w}}} \right)$ in the r.h.s. of Eq. (106) is a scalar field; hence, it may be inserted in the fundamental spatial averaging theorem Eq. (105), which yields

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle \cdot {\varvec{w}}=\nabla \left\langle {\left( {{\varvec{a}}\cdot {\varvec{w}}} \right) } \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{a}}\cdot {\varvec{w}}} \right) {\text{ d }}A}. \end{aligned}$$

(107)

Using the fact that w is uniform, Eq. (107) may be written as

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle \cdot {\varvec{w}}=\nabla \left\langle {\varvec{a}} \right\rangle \cdot {\varvec{w}}+\left( \frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } {\varvec{a}}\, {\text{ d }}A \right) \cdot {\varvec{w}}. \end{aligned}$$

(108)

Since Eq. (108) is valid for any uniform vector ${\varvec{w}}$, it may be reduced to

1.2 Theorem 2

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle =\nabla \left\langle {\varvec{a}} \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } {\varvec{a}}\; {\text{ d }}A. \end{aligned}$$

(109)

To obtain an equivalent theorem for the divergence of a vector field ${\varvec{a}}$, the procedure proposed at Problem 1.7 in Whitaker (1999) is used, i.e., the double contraction of Eq. (109) is made with the identity tensor ${\varvec{I}}$, which yields

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle :{\varvec{I}}=\nabla \left\langle {\varvec{a}} \right\rangle :{\varvec{I}}+\left( {\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } {\varvec{a}}\; {\text{ d }}A} \right) :{\varvec{I}}. \end{aligned}$$

(110)

It can be shown with elementary tensor algebra that Eq. (110) may be written as

1.3 Theorem 3

$$\begin{aligned} \left\langle {\nabla \cdot {\varvec{a}}} \right\rangle =\nabla \cdot \left\langle {\varvec{a}} \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } \cdot {\varvec{a}}\; {{\text{ d }}A}. \end{aligned}$$

(111)

To obtain an equivalent theorem for the divergence of a tensor field ${\varvec{C}}$, the expression $\left\langle {\nabla \cdot {\varvec{C}}} \right\rangle$ is multiplied by an arbitrary uniform vector w, which yields

$$\begin{aligned} \left\langle {\nabla \cdot {\varvec{C}}} \right\rangle \cdot {\varvec{w}}=\left\langle {\nabla \cdot \left( {\varvec{C}}\cdot {\varvec{w}} \right) } \right\rangle . \end{aligned}$$

(112)

The equality given in Eq. (112) may be demonstrated with tensor analysis. The expression $\left( {{\varvec{C}}\cdot {\varvec{w}}} \right)$ in the r.h.s. of Eq. (112) is a vector field; hence, it may be inserted in the spatial averaging theorem Eq. (111), which yields

$$\begin{aligned} \left\langle {\nabla \cdot {\varvec{C}}} \right\rangle \cdot {\varvec{w}}=\nabla \cdot \left\langle {{\varvec{C}}\cdot {\varvec{w}}} \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } \cdot \left( {{\varvec{C}}\cdot {\varvec{w}}} \right) \;{{\text{ d }}A}. \end{aligned}$$

(113)

Using the fact that w is uniform, Eq. (113) may be written as

$$\begin{aligned} \left\langle {\nabla \cdot {\varvec{C}}} \right\rangle \cdot {\varvec{w}}=\left( {\nabla \cdot \left\langle {\varvec{C}} \right\rangle } \right) \cdot {\varvec{w}}+\left( \frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } \cdot {\varvec{C}}\, {{\text{ d }}A} \right) \cdot {\varvec{w}}. \end{aligned}$$

(114)

Since Eq. (114) is valid for any uniform vector w, it may be reduced to

1.4 Theorem 4

$$\begin{aligned} \left\langle {\nabla \cdot {\varvec{C}}} \right\rangle =\nabla \cdot \left\langle {\varvec{C}} \right\rangle +\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } \cdot {\varvec{C}}\; {{\text{ d }}A}. \end{aligned}$$

(115)

This theorem has already been used by Gray and O’Neill (1976). Another expression of interest is the transpose of a vector gradient, i.e., $\left( {\nabla {\varvec{a}}} \right) ^{\dagger }$. This term appears, for example, in the viscous stress tensor expression for Newtonian fluid. The first step is to apply the transpose operator to Eq. (109), i.e.,

$$\begin{aligned} \left\langle {\nabla {\varvec{a}}} \right\rangle ^{\dagger }=\left( {\nabla \left\langle {\varvec{a}} \right\rangle } \right) ^{\dagger }+\left( {\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {{\varvec{n}}_{\alpha \beta } {\varvec{a}}\, {{\text{ d }}A}}} \right) ^{\dagger }. \end{aligned}$$

(116)

The transpose and integral operator being commutable, Eq. (116) may be written as

$$\begin{aligned} \left\langle {\left( {\nabla {\varvec{a}}} \right) ^{\dagger }} \right\rangle =\left( {\nabla \left\langle {\varvec{a}} \right\rangle } \right) ^{\dagger }+\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\left( {{\varvec{n}}_{\alpha \beta } {\varvec{a}}} \right) ^{\dagger } {{\text{ d }}A}}. \end{aligned}$$

(117)

and with tensor algebra one may prove that the transpose of a dyadic product $\left( {{\varvec{n}}_{\alpha \beta } {\varvec{a}}} \right) ^{\dagger }$ becomes ${\varvec{an}}_{\alpha \beta }$, which leads to

1.5 Theorem 5

$$\begin{aligned} \left\langle {\left( {\nabla {\varvec{a}}} \right) ^{\dagger }} \right\rangle =\left( {\nabla \left\langle {\varvec{a}} \right\rangle } \right) ^{\dagger }+\frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{an}}_{\alpha \beta } \; {{\text{ d }}A}. \end{aligned}$$

(118)

Another expression of interest has the form $\left( {\nabla \cdot {\varvec{a}}} \right) {\varvec{I}}$. This term appears, for example, in the viscous stress tensor expression for Newtonian fluid. To obtain a spatial averaging theorem for this expression, the identity tensor ${\varvec{I}}$ is extracted from the averaging operator , i.e.,

$$\begin{aligned} \left\langle {\left( {\nabla \cdot {\varvec{a}}} \right) {\varvec{I}}} \right\rangle =\left\langle {\nabla \cdot {\varvec{a}}} \right\rangle {\varvec{I}}. \end{aligned}$$

(119)

The expression $\left\langle {\nabla \cdot {\varvec{a}}} \right\rangle$ in Eq. (119) may be developed by Eq. (111). Hence, Eq. (119) may be written as

1.6 Theorem 6

$$\begin{aligned} \left\langle {\left( {\nabla \cdot {\varvec{a}}} \right) {\varvec{I}}} \right\rangle =\left( {\nabla \cdot \left\langle {\varvec{a}} \right\rangle } \right) {\varvec{I}}+\left( \frac{1}{V}\int \limits _{\Gamma _{\alpha \beta }} {\varvec{n}}_{\alpha \beta } \cdot {\varvec{a}}\; {\text{ d }}A \right) {\varvec{I}}. \end{aligned}$$

(120)

Theorems 5 and 6 have already been used by Gray and O’Neill (1976), and also by Whitaker (2002). Other forms of the spatial averaging theorems have also been developed by Del Rio and Whitaker (2000) for electrodynamics, and by Ochoa-Tapia et al. (1993) for surface diffusion, but they are not used in this text.

Appendix 3: Estimation of $K\left\langle {y_A} \right\rangle _\alpha$

The value of the expression of $K\left\langle {y_A} \right\rangle _\alpha$ in the anode catalyst layer of a polymer electrolyte fuel cell (where species $A$ is hydrogen) is to be estimated in this section.

First, the current density $i$ of a fuel cell is converted into a volumetric mass source in the anode catalyst layer by the relation

$$\begin{aligned} \hbox {volumetric mass source}={iM_{\mathrm{H}_2}}/{2L_{\text {III}} F}, \end{aligned}$$

(121)

where the current density $i$ is of the order of $1\times 10^{4}\hbox { A/m}^{2}$ (Barbir 2013), the thickness $L_\mathrm{III}$ of catalyst layers (see Layer III in Fig. 3) is of the order of $3\times \hbox {10}^{-4}\hbox {m}$ (Ju and Wang 2004), the molar mass of hydrogen $\mathrm{H}_2$ is $2\times 10^{-3}\hbox { kg/mol}$ (Çengel and Boles 2001), and the Faraday constant $F$ is equal to $96487\hbox { C/mol}$ (Ju and Wang 2004).

Moreover, one has to recall that the volumetric mass source expression given in Eq. (21) is $\left\langle \rho \right\rangle _\alpha a_\mathrm{V} K\left\langle {y_A} \right\rangle _\alpha$. The surface density $a_V$ is of the order of $1/{l_\alpha }$, where $l_\alpha \approx 3\times 10^{-5}\hbox { m}$ (Maheshwari et al. 2008), and the density of a mixture of hydrogen and steam at standard pressure and temperature (for a relative humidity of 1) is on the order of $0.35\hbox { kg/m}^{3}$. Equating the volumetric mass source expression for a PEMFC anode catalyst given in Eq. (121) to the volumetric mass source expression given in Eq. (21) leads to

$$\begin{aligned} \left\langle \rho \right\rangle _\alpha a_\mathrm{V} K\left\langle {y_A} \right\rangle _\alpha ={iM_{\mathrm{H}_2}}/{2L_{\text {III}} F}, \end{aligned}$$

(122)

and isolating the expression $K\left\langle {y_A} \right\rangle _\alpha$ yields

$$\begin{aligned} K\left\langle {y_A} \right\rangle _\alpha ={iM_{\mathrm{H}_2}}/2L_\mathrm{{III}} F\left\langle \rho \right\rangle _\alpha a_\mathrm{V}. \end{aligned}$$

(123)

Using the values given above, the order of magnitude of $K\left\langle {y_A} \right\rangle _\alpha$ is $3\times 10^{-5}\hbox {m}/\hbox {s}$.

Appendix 4: Constraints for $\tilde{{\varvec{u}}}$ at $\Gamma _{\alpha \beta }$

In the course of the macroscopic momentum equation development performed in Sect. 4.2, it was asserted (without demonstration) that the expression ${\varvec{n}}_{\alpha \beta } \cdot \nabla _\dagger \tilde{{\varvec{u}}}$ present in Eq. (47) was equal to zero at the surface $\Gamma _{\alpha \beta }$ (the reader should recall that in this paper, the notation $\nabla _\dagger \tilde{{\varvec{u}}}$ is used for $\left( {\nabla \tilde{{\varvec{u}}}} \right) ^{\dagger })$. This assertion is demonstrated in the following paragraphs.

The first step is to obtain a practical expression equivalent to the constraint on $\tilde{{\varvec{u}}}$ given in Eq. (77), i.e.,

$$\begin{aligned} \tilde{{\varvec{u}}}=-\left\langle {\varvec{u}} \right\rangle _\alpha \;\;\; \hbox { at } \Gamma _{\alpha \beta }. \end{aligned}$$

(124)

Using the approximation that the value of $\left\langle {\varvec{u}} \right\rangle _\alpha$ undergoes negligible change with position within a REV, the constraint Eq. (124) means that the value of $\tilde{{\varvec{u}}}$ does not change when the position considered is on the surface $\Gamma _{\alpha \beta }$. This can be mathematically expressed as

$$\begin{aligned} \nabla _S \tilde{{\varvec{u}}}=0\;\;\;\; \hbox { at } \Gamma _{\alpha \beta }. \end{aligned}$$

(125)

The surface gradient operator $\nabla _S$ present in Eq. (125) is defined as

$$\begin{aligned} \nabla _S =\left( {{\varvec{P}}\cdot \nabla } \right) \;\;\;\hbox { at } \Gamma _{\alpha \beta }, \end{aligned}$$

(126)

where the projection tensor ${\varvec{P}}$ is defined as ${\varvec{P}}\equiv {\varvec{I}}-{\varvec{n}}_{\alpha \beta } {\varvec{n}}_{\alpha \beta }$ (Ochoa-Tapia et al. 1993). Using these definitions of ${\varvec{P}}$ and $\nabla _S$ into Eq. (125) leads to

$$\begin{aligned} \nabla \tilde{{\varvec{u}}}-{\varvec{n}}_{\alpha \beta } {\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}=0 \;\;\;\hbox { at }\Gamma _{\alpha \beta }. \end{aligned}$$

(127)

The general relations $\left( {{\varvec{T}}\cdot \nabla } \right) {\varvec{a}}\equiv {\varvec{T}}\cdot \nabla {\varvec{a}}$ and ${\varvec{I}}\cdot \nabla {\varvec{a}}\equiv \nabla {\varvec{a}}$, which hold for any vector ${\varvec{a}}$ and tensor ${\varvec{T}}$, were used to obtain Eq. (127) from Eq. (125). Finally, Eq. (127) is rearranged to obtain the expression

$$\begin{aligned} \text {Constraint }\, \textit{1}\;\;\;\;\;\;\; \nabla \tilde{{\varvec{u}}}={\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) \;\;\;\;\hbox { at }\Gamma _{\alpha \beta }, \end{aligned}$$

(128)

where the general relation ${\varvec{aa}}\cdot \nabla {\varvec{b}}\equiv {\varvec{a}}\left( {{\varvec{a}}\cdot \nabla {\varvec{b}}} \right)$, which holds for any vector fields ${\varvec{a}}$ and ${\varvec{b}}$, was used. Notice that Eq. (128) is just another way to write the constraint given by Eq. (124).

The second step is to write the other constraint on $\tilde{{\varvec{u}}}$ that was given in Sect. 5.1 (see Eq. (61)), i.e.,

$$\begin{aligned} \nabla \cdot \tilde{{\varvec{u}}}=0. \end{aligned}$$

(129)

Since this expression is equal to the scalar zero, one may multiply Eq. (129) by the vector ${\varvec{n}}_{\alpha \beta }$, so that the r.h.s. of this equation becomes a vector equal to zero, i.e., ${\varvec{n}}_{\alpha \beta } \left( {\nabla \cdot \tilde{{\varvec{u}}}} \right) =0$. Moreover, it is easy to show with tensor algebra that, for any vector field ${\varvec{a}}$, the relation $\nabla \cdot {\varvec{a}}\equiv \nabla {\varvec{a}}:{\varvec{I}}$ is true; hence, Eq. (129) becomes

$$\begin{aligned} \text {Constraint }\, \textit{2}\;\;\;\; \underbrace{{\varvec{n}}_{\alpha \beta }}_{\hbox {vector}}\underbrace{\left( {\nabla \tilde{{\varvec{u}}}:{\varvec{I}}} \right) }_{\hbox {scalar}}=\underbrace{0}_{\begin{array}{c} \hbox {nul} \\ \hbox {vector} \\ \end{array}} \end{aligned}$$

(130)

Notice that the constraint given by Eq. (130) is valid everywhere in the $\alpha$ phase, including the surface $\Gamma _{\alpha \beta }$ where the boundary conditions for $\tilde{{\varvec{u}}}$ applies.

The objective is to prove, with the help of the two constraints given by Eq. (128) and Eq. (130), that ${\varvec{n}}_{\alpha \beta } \cdot \nabla _\dagger \tilde{{\varvec{u}}}=0$ at $\Gamma _{\alpha \beta }$. Hence, the next step consists in writing the expression

$$\begin{aligned} {\varvec{n}}_{\alpha \beta } \cdot \nabla _\dagger \tilde{{\varvec{u}}}={\varvec{d}}\;\;\;\hbox { at }\Gamma _{\alpha \beta }, \end{aligned}$$

(131)

where ${\varvec{d}}$ is the unknown vector to find. Using the fact that ${\varvec{a}}\cdot \nabla _\dagger {\varvec{b}}\equiv \nabla {\varvec{b}}\cdot {\varvec{a}}$ for any vector fields ${\varvec{a}}$ and ${\varvec{b}}$, Eq. (131) is rewritten as

$$\begin{aligned} \nabla \tilde{{\varvec{u}}}\cdot {\varvec{n}}_{\alpha \beta } ={\varvec{d}} \end{aligned}$$

(132)

Since the expression given by Eq. (130) is equal to zero, one can simply subtract Eq. (130) from Eq. (132) so as to obtain

$$\begin{aligned} \nabla \tilde{{\varvec{u}}}\cdot {\varvec{n}}_{\alpha \beta } -\underbrace{{\varvec{n}}_{\alpha \beta } \left( {\nabla \tilde{{\varvec{u}}}:{\varvec{I}}} \right) }_{\begin{array}{c} \hbox {zero} \\ \hbox {by Eq. (130)} \\ \end{array}}={\varvec{d}} \end{aligned}$$

(133)

Then, the constraint given in Eq. (128), (i.e., $\nabla \tilde{{\varvec{u}}}={\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) )$ is used by inserting directly that expression where $\nabla \tilde{{\varvec{u}}}$ is present in Eq. (133). Hence, Eq. (133) becomes

$$\begin{aligned} \left( {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) \cdot {\varvec{n}}_{\alpha \beta } -{\varvec{n}}_{\alpha \beta } \left( {\left[ {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right] :{\varvec{I}}} \right) ={\varvec{d}}. \end{aligned}$$

(134)

The strategy is to prove that the second term in the l.h.s. of Eq. (134) is equivalent to the first, which would prove that ${\varvec{d}}$ is equal to zero. To do so, the term $\left[ {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right] :{\varvec{I}}$ in Eq. (134) is transformed into the expression ${\varvec{n}}_{\alpha \beta } \cdot \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right)$, using a relation that hold for any vector field ${\varvec{a}}$ and ${\varvec{b}}$, i.e., ${\varvec{ab}}:{\varvec{I}}\equiv {\varvec{a}}\cdot {\varvec{b}}$. In this process, the expression ${\varvec{n}}_{\alpha \beta }$ was associated to ${\varvec{a}}$ and $\left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right)$ was associated to ${\varvec{b}}$. Therefore, Eq. (134) becomes

$$\begin{aligned} \left( {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) \cdot {\varvec{n}}_{\alpha \beta } -{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) ={\varvec{d}}. \end{aligned}$$

(135)

The general relation ${\varvec{a}}\left( {{\varvec{b}}\cdot {\varvec{c}}} \right) \equiv {\varvec{bc}}\cdot {\varvec{a}}$, which holds for any vector fields ${\varvec{a}},\, {\varvec{b}}$, and ${\varvec{c}}$, is used to transform the expression ${\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right)$ into $\left( {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) \cdot {\varvec{n}}_{\alpha \beta }$. In this process, the expression ${\varvec{n}}_{\alpha \beta }$ was associated to ${\varvec{a}}$ and ${\varvec{b}}$, and the expression $\left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right)$ was associated to ${\varvec{c}}$ . Therefore, Eq. (135) becomes

$$\begin{aligned} \underbrace{\left( {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) \cdot {\varvec{n}}_{\alpha \beta } -\left( {{\varvec{n}}_{\alpha \beta } \left( {{\varvec{n}}_{\alpha \beta } \cdot \nabla \tilde{{\varvec{u}}}} \right) } \right) \cdot {\varvec{n}}_{\alpha \beta }}_{\hbox {zero}}={\varvec{d}}, \end{aligned}$$

(136)

where the l.h.s. is identically equal to zero.

To summarize, by transforming the two constraints given by Eqs. (124) and (129) into Eqs. (128) and (130), respectively, it was possible to prove that the value of ${\varvec{d}}$ in Eq. (131) is equal to zero. In other words, it was proved that ${\varvec{n}}_{\alpha \beta }\cdot \nabla _\dagger \tilde{{\varvec{u}}}=0$ at $\Gamma _{\alpha \beta }$.