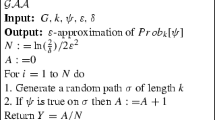Verification and control of partially observable probabilistic systems

Abstract

We present automated techniques for the verification and control of partially observable, probabilistic systems for both discrete and dense models of time. For the discrete-time case, we formally model these systems using partially observable Markov decision processes; for dense time, we propose an extension of probabilistic timed automata in which local states are partially visible to an observer or controller. We give probabilistic temporal logics that can express a range of quantitative properties of these models, relating to the probability of an event’s occurrence or the expected value of a reward measure. We then propose techniques to either verify that such a property holds or synthesise a controller for the model which makes it true. Our approach is based on a grid-based abstraction of the uncountable belief space induced by partial observability and, for dense-time models, an integer discretisation of real-time behaviour. The former is necessarily approximate since the underlying problem is undecidable, however we show how both lower and upper bounds on numerical results can be generated. We illustrate the effectiveness of the approach by implementing it in the PRISM model checker and applying it to several case studies from the domains of task and network scheduling, computer security and planning.

1 Introduction

Guaranteeing the correctness of complex computerised systems often needs to take into account quantitative aspects of system behaviour. This includes the modelling of probabilistic phenomena, such as failure rates for physical components, uncertainty arising from unreliable sensing of a continuous environment, or the explicit use of randomisation to break symmetry. It also includes timing characteristics, such as time-outs or delays in communication or security protocols. To further complicate matters, such systems are often nondeterministic because their behaviour depends on inputs or instructions from some external entity such as a controller or scheduler.

Automated verification techniques such as probabilistic model checking have been successfully used to analyse quantitative properties of probabilistic systems across a variety of application domains, including wireless communication protocols, computer security and task scheduling. These systems are commonly modelled using Markov decision processes (MDPs), if assuming a discrete notion of time, or probabilistic timed automata (PTAs), if using a dense model of time. On these models, we can consider two problems: verification that it satisfies some formally specified property for any possible resolution of nondeterminism; or, dually, synthesis of a controller (i.e., a means to resolve nondeterminism) under which a property is guaranteed to hold. For either case, an important consideration is the extent to which the system’s state is observable to the entity controlling it. For example, to verify that a security protocol is functioning correctly, it may be essential to model the fact that some data held by a participant is not externally visible; or, when synthesising an optimal schedule for sending packets over a network, a scheduler may not be implementable in practice if it bases its decisions on information about the state of the network that is unavailable due to the delays and costs associated with probing it.

Partially observable MDPs (POMDPs) are a natural way to extend MDPs in order to tackle this problem. However, the analysis of POMDPs is considerably more difficult than MDPs since key problems are undecidable (Madani et al. 2003). A variety of verification problems have been studied for these models (see, e.g., de Alfaro 1999; Baier et al. 2008; Chatterjee et al. 2013) and the use of POMDPs is common in fields such as AI and planning (Cassandra 1998), but there is limited progress in the development of practical techniques for probabilistic verification in this area, or exploration of their applicability.

In this paper, we present novel techniques for verification and control of partially observable, probabilistic systems under both discrete and dense models of time. We use POMDPs in the case of discrete-time models and, for dense time, propose a model called partially observable probabilistic timed automata (POPTAs), which extends the existing model of PTAs with a notion of partial observability. The semantics of a POPTA is an infinite-state POMDP. In order to specify verification and control problems on POMDPs and POPTAs, we define temporal logics to express properties of these models relating to the probability of an event (e.g., the probability of some observation eventually being made) or the expected value of various reward measures (e.g., the expected time until some observation). Nondeterminism in both a POMDP and a POPTA is resolved by a strategy that decides which actions to take and when to take them, based only on the history of observations (not states). The core problems we address are how to verify that a temporal logic property holds for all possible strategies, and how to synthesise a strategy under which the property holds.

In order to achieve this, we use a combination of techniques. To analyse a POMDP, we use grid-based techniques (Lovejoy et al. 1991; Yu and Bertsekas 2004), which transform it to a fully observable but continuous-space MDP and then approximate its solution based on a finite set of grid points. We use this to construct and solve a strategy of the POMDP. The result is a pair of lower and upper bounds on the property of interest for the POMDP. If this is not precise enough, we can refine the grid and repeat. In the case of POPTAs, we develop a digital clocks discretisation, which extends the existing notion for PTAs (Kwiatkowska et al. 2006). The discretisation reduces the analysis to a finite POMDP, and hence we can use the techniques we have developed for analysing POMDPs. We define the conditions under which temporal logic properties are preserved by the discretisation step and prove the correctness of the reduction under these conditions.

We implemented these methods in a prototype tool based on PRISM (Kwiatkowska et al. 2011; PRISM), and investigated their applicability by developing a number of case studies including: wireless network scheduling, a task scheduling problem, a covert channel prevention device (the NRL pump) and a non-repudiation protocol. Despite the undecidability of the POMDP problems we consider, we show that useful results can be obtained, often with precise bounds. In each case study, partial observability, nondeterminism, probability and, in the case of the dense-time models, real-time behaviour are all crucial ingredients to the analysis. This is a combination not supported by any existing techniques or tools.

A preliminary conference version of this paper, was published as Norman et al. (2015).

1.1 Related work

POMDPs are common in fields such as AI and planning: they have many applications (Cassandra 1998) and tool support exists (Poupart 2005). However, unlike verification, the focus in these fields is usually on finite-horizon and discounted reward objectives. Early undecidability for key problems can be found in, e.g., Madani et al. (2003). POMDPs have also been applied to problems such as scheduling in wireless networks since, in practice, information about the state of wireless connections is often unavailable and varies over time; see e.g. Johnston and Krishnamurthy (2006), Li and Neely (2011), Yang et al. (2011), Jagannathan et al. (2013), and Gopalan et al. (2015).

POMDPs have also been studied by the formal verification community, see e.g. de Alfaro (1999), Baier et al. (2008), and Chatterjee et al. (2013), establishing undecidability and complexity results for various qualitative and quantitative verification problems. In the case of qualitative analysis, Chatterjee et al. (2015) presents an approach for the verification and synthesis of POMDPs against LTL properties when restricting to finite-memory strategies. This has been implemented and applied to an autonomous system (Svoren̂ová et al. 2015). For quantitative properties, the recent work of Chatterjee (2016) extends approaches developed for finite-horizon objectives to approximate the minimum expected reward of reaching a target (while ensuring the target is reached with probability 1), under the requirement that all rewards in the POMDP are positive.

Work in this area often also studies related models such as Rabin’s probabilistic automata (Baier et al. 2008), which can be seen as a special case of POMDPs, and partially observable stochastic games (POSGs) (Chatterjee and Doyen 2014), which generalise them. More practically oriented work includes: Giro andRabe (2012), which proposes a counter-example-driven refinement method to approximately solve MDPs in which components have partial observability of each other; and Cerný et al. (2011), which synthesises concurrent program constructs using a search over memoryless strategies in a POSG.

Theoretical results (Bouyer et al. 2003) and algorithms (Cassez et al. 2007; Finkbeiner and Peter 2012) have been developed for synthesis of partially observable timed games. In Bouyer et al. (2003), it is shown that the synthesis problem is undecidable and, if the resources of the controller are fixed, decidable but prohibitively expensive. The algorithms require constraints on controllers: in Cassez et al. (2007), controllers only respond to changes made by the environment and, in Finkbeiner and Peter (2012), their structure must be fixed in advance. We are not aware of any work for probabilistic real-time models in this area.

1.2 Outline

Section 2 describes the discrete-time models of MDPs and POMDPs, and Sect. 3 presents our approach for POMDP verification and strategy synthesis. In Sect. 4, we introduce the dense-time models of PTAs and POPTAs, and then, in Sect. 5, give our verification and strategy synthesis approach for POPTAs using digital clocks. Section 6 describes the implementation of our techniques for analysing POMDPs and POPTAs in a prototype tool, and demonstrates its applicability using several case studies. Finally, Sect. 7 concludes the paper.

2 Partially observable Markov decision processes

In this section, we consider systems exhibiting probabilistic, nondeterministic and discrete-time behaviour. We first introduce MDPs, and then describe POMDPs, which extend these to include partial observability. For a more detailed tutorial on verification techniques for MDPs, we refer the reader to, for example, Forejt et al. (2011).

2.1 Markov decision processes

Let ${ Dist }(X)$ denote the set of discrete probability distributions over a set X, $\delta _{x}$ the distribution that selects $x \in X$ with probability 1, and $\mathbb {R}$ the set of non-negative real numbers.

Definition 1

(MDP) An MDP is a tuple $\mathsf{M}= (S,{\bar{s}},A,P, R )$ where:

• S is a set of states;

• ${\bar{s}}\in S$ is an initial state;

• A is a set of actions;

• $P : S \times A \rightarrow { Dist }(S)$ is a (partial) probabilistic transition function;

• $R = ( R _S, R _A)$ is a reward structure where $R _S : S \rightarrow \mathbb {R}$ is a state reward function and $R _A : S \times A \rightarrow \mathbb {R}$ an action reward function.

An MDP $\mathsf{M}$ represents the evolution of a system exhibiting both probabilistic and nondeterministic behaviour through states from the set S. Each state $s\in S$ of $\mathsf{M}$ has a set $A(s)\mathop {=}\limits ^{\mathrm{def}}\{a\in A \mid P(s,a) \text { is defined}\}$ of available actions. The choice between which available action is chosen in a state is nondeterministic. In a state s, if action $a\in A(s)$ is selected, then the probability of moving to state $s'$ equals $P(s,a)(s')$.

A path of $\mathsf{M}$ is a finite or infinite sequence $\pi =s_0 \xrightarrow {a_0} s_1 \xrightarrow {a_1} \cdots$, where $s_i\in S$, $a_i\in A(s_i)$ and $P(s_i,a_i)(s_{i+1}){>}0$ for all $i \in \mathbb {N}$. The $(i+1)$th state $s_i$ of path $\pi$ is denoted $\pi (i)$ and, if $\pi$ is finite, $last (\pi )$ denotes its final state. We write $FPaths _{\mathsf{M}}$ and $IPaths _{\mathsf{M}}$, respectively, for the set of all finite and infinite paths of $\mathsf{M}$ starting in the initial state ${\bar{s}}$. MDPs are also annotated with rewards, which can be used to model a variety of quantitative measures of interest. A reward of $R (s)$ is accumulated when passing through state s and a reward of $R (s,a)$ when taking action a from state s.

A strategy of $\mathsf{M}$ (also called a policy or scheduler) is a way of resolving the choice of action in each state, based on the MDP’s execution so far.

Definition 2

(Strategy) A strategy of an MDP $\mathsf{M}=(S,{\bar{s}},A,P, R )$ is a function ${\sigma }: FPaths _\mathsf{M}{\rightarrow } { Dist }( A )$ such that, for any $\pi \in FPaths _\mathsf{M}$, we have ${\sigma }(\pi )(a){>}0$ only if $a\in A( last (\pi ))$. Let ${\Sigma }_\mathsf{M}$ denote the set of all strategies of ${\mathcal {M}}$.

A strategy is memoryless if its choices only depend on the current state, finite-memory if it suffices to switch between a finite set of modes and deterministic if it always selects an action with probability 1.

When $\mathsf{M}$ is under the control of a strategy ${\sigma }$, the resulting behaviour is captured by a probability measure ${ Pr _{\mathsf{M}}^{{\sigma }}}$ over the infinite paths of $\mathsf{M}$ (Kemeny et al. 1976). Furthermore, given a random variable $f : IPaths _{\mathsf{M}} {\rightarrow }\mathbb {R}$ over the infinite paths of $\mathsf{M}$, using the probability measure ${ Pr _{\mathsf{M}}^{{\sigma }}}$, we can define the expected value of the variable f with respect to the strategy $\sigma$, denoted $\mathbb {E}_{\mathsf{M}}^{{\sigma }}(f)$.

2.2 Partially observable Markov decision processes

POMDPs extend MDPs by restricting the extent to which their current state can be observed, in particular by strategies that control them. In this paper (as in, e.g., Baier et al. 2008; Chatterjee et al. 2013), we adopt the following notion of observability.

Definition 3

(POMDP) A POMDP is a tuple $\mathsf{M}= (S,{\bar{s}},A,P, R ,\mathcal {O}, obs )$ where:

• $(S,{\bar{s}},A,P, R )$ is an MDP;

• $\mathcal {O}$ is a finite set of observations;

• $obs : S \rightarrow \mathcal {O}$ is a labelling of states with observations;

such that, for any states $s,s'\in S$ with $obs (s)= obs (s')$, their available actions must be identical, i.e., $A(s)=A(s')$.

The current state s of a POMDP cannot be directly determined, only the corresponding observation $obs (s)\in \mathcal {O}$. The requirement on available actions in Definition 3 follows from the fact that, if states have different actions available, then they are not observationally equivalent as the available actions are not hidden, and hence should not have the same observation.

More general notions of observations are sometime used, e.g., that depend also on the previous action taken or are probabilistic. However, as demonstrated by Chatterjee (2016), given a POMDP with the most general notion of observations (both probabilistic and dependent on the previous action), we can construct an equivalent (polynomially larger) POMDP of the form given in Definition 3. In addition, our analysis of probabilistic verification case studies where partial observation is needed (see, e.g., Sect. 6) suggests that this simpler notion of observability will often suffice in practice. To ease presentation, we assume that the initial state is observable, i.e., there exists ${\bar{o}}\in \mathcal {O}$ such that $obs (s)={\bar{o}}$ if and only if $s={\bar{s}}$.

The notions of paths, strategies and probability measures given above for MDPs transfer directly to POMDPs. However, the set ${\Sigma }_\mathsf{M}$ of all strategies for a POMDP $\mathsf{M}$ only includes observation-based strategies.

Definition 4

(Observation-based strategy) A strategy of a POMDP $\mathsf{M}= (S,{\bar{s}},A,P,R,\mathcal {O}, obs )$ is a function ${\sigma }: FPaths _\mathsf{M}{\rightarrow } { Dist }( A )$ such that:

• $\sigma$ is a strategy of the MDP $(S,{\bar{s}},A,P,R)$;

• for any paths $\pi =s_0 \xrightarrow {a_0}s_1 \xrightarrow {a_1}\cdots s_n$ and $\pi '=s_0' \xrightarrow {a_0'} s_1'\xrightarrow {a_1'} \cdots s_n'$ satisfying $obs (s_i)= obs (s_i')$ and $a_i=a_i'$ for all i, we have ${\sigma }(\pi )={\sigma }(\pi ')$.

Let ${\Sigma }_\mathsf{M}$ denote the set of all (observation-based) strategies of $\mathsf{M}$.

Key properties for MDPs and POMDPs are the probability of reaching a target and the expected reward cumulated until this occurs (where we assume that the expected value is infinite if there is a non-zero probability of the target not being reached). Let O denote the target (i.e., a set of states for an MDP and a set of observations for a POMDP). Under a specific strategy ${\sigma }$ of an MDP or POMDP $\mathsf{M}$, we denote these two properties by ${ Pr _{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)}$ and ${\mathbb {E}_{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)}$, respectively.

Usually, we are interested in the optimal (minimum or maximum) values $\smash {{ Pr _{\mathsf{M}}^{opt}({\texttt {F}\ }O)}}$ and $\smash {{\mathbb {E}_{\mathsf{M}}^{opt}({\texttt {F}\ }O)}}$, where $opt\in \{\min ,\max \}$. For MDP or POMDP $\mathsf{M}$:

$$\begin{aligned} \begin{array}{rclcrcl} &{}&{}{ Pr _{\mathsf{M}}^{\min }({\texttt {F}\ }O)} \mathop {=}\limits ^{\mathrm{def}}\inf \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} { Pr _{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)} &{}&{} {\mathbb {E}_{\mathsf{M}}^{\min }({\texttt {F}\ }O)} &{} \mathop {=}\limits ^{\mathrm{def}}&{} \inf \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} {\mathbb {E}_{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)} \\ &{}&{}{ Pr _{\mathsf{M}}^{\max }({\texttt {F}\ }O)}\mathop {=}\limits ^{\mathrm{def}}\sup \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} { Pr _{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)} &{}&{} {\mathbb {E}_{\mathsf{M}}^{\max }({\texttt {F}\ }O)} &{} \mathop {=}\limits ^{\mathrm{def}}&{} \sup \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} {\mathbb {E}_{\mathsf{M}}^{{\sigma }}({\texttt {F}\ }O)} \end{array} \end{aligned}$$

Note that the class of strategies ${\Sigma }_\mathsf{M}$ analysed in the above is different depending on whether $\mathsf{M}$ is an MDP or POMDP (see Definitions 2 and 4, respectively). In the case of MDPs, deterministic and memoryless strategies achieve optimal values. This allows the use of efficient computational techniques such as policy iteration, which builds a sequence of strategies until an optimal one is reached, and value iteration, which computes increasingly precise approximations to the optimal probability or expected value (see for example Puterman et al. 1994). However, in the case of POMDPs, this no longer holds. In fact, determining the optimal probabilities and expected rewards defined above is undecidable (Madani et al. 2003), making exact solution intractable. Instead, the optimal value can be approximated, for example via analysis of the belief MDP, whose construction we will discuss shortly.

Fig. 1

McCallum’s maze problem (McCallum 1993)

Example 1

As an example POMDP, we consider a maze, originally introduced by McCallum  (1993). The example concerns a robot being placed uniformly at random in a maze and then trying to find its way to a certain target location. The maze is presented in Fig. 1 and comprises 11 locations labelled from ‘0’ to ‘10’. There are four actions that the robot can perform in each location, corresponding to the four directions it can move: north, east, south and west. Performing such an action moves the robot one location in that direction (if moving in that direction means hitting a wall, the robot remains where it is). The robot cannot see its current location, but only what walls surround it. Therefore, for example, the locations labelled ‘5’, ‘6’ and ‘7’ yield the same observation, since the robot can only observe that there are walls to the east and west. The goal of the robot is to reach the target location labelled ‘10’, and hence we associate a distinct observation with this location.

We find that the optimal (minimum) expected number of moves to reach the target is 4.3. If we instead consider a fully observable model (i.e., an MDP), then the optimal expected number of moves is 3.9. Considering a strategy of the POMDP that achieves the optimal value, if the robot initially observes that the only walls are on the east and west, then the strategy believes with equal probability that the robot is in one of the locations labelled ‘5’, ‘6’ and ‘7’. The strategy moves the robot north which allows it to learn which of these states the robot is actually in. More precisely, if the robot was in the location labelled ‘5’, then, after moving north, it will observe walls to the north and west, if it was in the location ‘6’ it will next observe only a wall to the north and, for the location labelled ‘7’, next observe walls to the north and east.

Note that, if the strategy knew the robot was in the location labelled ‘6’, the optimal move would be south as opposed to north. When the robot initially observes walls to the north and south, the strategy does not know if it is in the location labelled ‘1’ or the one labelled ‘3’. Here the strategy can either choose east or west. When performing either action, the strategy will be able to learn the robot’s position, while moving the robot closer to the target in one case and further away in the other. Once the strategy knows the robot’s position, it can easily determine the optimal route for the robot to reach the target.

Beliefs   Given a POMDP $\mathsf{M}$ we can construct a corresponding belief MDP ${\mathcal {B}}(\mathsf{M})$: an equivalent (fully observable) MDP, whose (continuous) state space comprises beliefs, which are probability distributions over the state space of $\mathsf{M}$. Intuitively, although we may not know which of several observationally-equivalent states we are currently in, we can determine the likelihood of being in each one, based on the probabilistic behaviour of $\mathsf{M}$. The formal definition is given below, and we include details of the construction in Appendix.

Definition 5

(Belief MDP) Let $\mathsf{M}=(S,{\bar{s}},A,P,R,\mathcal {O}, obs )$ be a POMDP. The belief MDP of $\mathsf{M}$ is given by ${\mathcal {B}}(\mathsf{M})=({ Dist }(S),\delta _{{\bar{s}}},A,P^{\mathcal {B}},R^{\mathcal {B}})$ where, for any beliefs $b,b'\in { Dist }(S)$ and action $a\in A$:

$$\begin{aligned} P^{\mathcal {B}}(b,a)(b')= & {} \sum _{s \in S} \; b(s) \cdot \left( \sum _{o \in \mathcal {O}\wedge b^{a,o}=b'} \sum _{s' \in S \wedge obs (s')=o} \; P(s,a)(s') \right) \\ R^{\mathcal {B}}_S(b)= & {} {\sum _{s \in S}} \; R_S(s) \cdot b(s) \\ R^{\mathcal {B}}_A(b,a)= & {} {\sum _{s \in S}} \; R_A(s,a) \cdot b(s) \end{aligned}$$

and $b^{a,o}$ is the belief reached from b by performing action a and observing o, i.e.:

$$\begin{aligned} b^{a,o}(s') \; = \; \left\{ \begin{array}{ll} \frac{\sum _{s \in S} P(s,a)(s') \cdot b(s)}{\sum _{s \in S} b(s) \cdot \left( \sum _{s^{{\scriptstyle \prime \prime }} \in S \wedge obs (s^{{\scriptstyle \prime \prime }})=o} P(s,a)(s'') \right) } &{} \quad {if\,\, obs (s')=o} \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

The optimal values for the probability and expected reward to reach a target in the belief MDP equal those for the POMDP, which is formally stated by the following proposition.

Proposition 1

If $\mathsf{M}=(S,{\bar{s}},A,P, R ,\mathcal {O}, obs )$ is a POMDP and $O \subseteq \mathcal {O}$ a set of observations, then:

$$\begin{aligned} { Pr _{\mathsf{M}}^{{opt}}({\texttt {F}\ }O)} = { Pr _{{\mathcal {B}}(\mathsf{M})}^{{opt}}({\texttt {F}\ }T_O)} \; \; \text{ and } \;\; \; \; {\mathbb {E}_{\mathsf{M}}^{{opt}}({\texttt {F}\ }O)} = {\mathbb {E}_{{\mathcal {B}}(\mathsf{M})}^{{opt}}({\texttt {F}\ }T_O)} \end{aligned}$$

where $T_O = \{ b \in { Dist }(S) \, | \, \forall s \in S .\, (b(s){>}0 {\rightarrow } obs (s)\in O) \}$ and ${opt}\in \{\min ,\max \}$.

2.3 Parallel composition of POMDPs

To facilitate the modelling of complex systems, we introduce a notion of parallel composition for POMDPs, which allows us to define a system as set of interacting components. Our definition extends the standard definition for MDPs and probabilistic automata (Segala and Lynch 1995). It is based on multi-way synchronisation over the same action by several components, as used in the process algebra CSP (Roscoe 1997) and the PRISM model checker (Kwiatkowska et al. 2011; PRISM), but this can easily be generalised to incorporate more flexible definitions of synchronisation. We will use parallel composition of POMDPs for modelling the case studies that we present in Sect. 6.

Definition 6

(Parallel composition of POMDPs) Consider any POMDPs $\mathsf{M}_i=(S_i,{\bar{s}}_i,A_i,P_i, R _i,\mathcal {O}_i, obs _i)$, for $i=1,2$. The parallel composition of $\mathsf{M}_1$ and $\mathsf{M}_2$ is the POMDP:

$$\begin{aligned} \mathsf{M}_1 \Vert \mathsf{M}_2 = (S_1 \times S_2,({\bar{s}}_1,{\bar{s}}_2),A_1\cup A_2, R ,\mathcal {O}_1 \times \mathcal {O}_2, obs ) \end{aligned}$$

where, for any $s=(s_1,s_2)$ and $a \in A_1 \cup A_2$, we have:

• if $a \in A_1 \cap A_2$, then $a \in A(s_1,s_2)$ if and only if $a \in A(s_1) \cap A(s_2)$ with

  $$\begin{aligned} P(s,a)(s') = P_1(s_1,a)(s_1') {\cdot } P_2(s_2,a)(s_2') \end{aligned}$$

  for all $s' = (s_1',s_2') \in S_1 \times S_2$ and $R_{A}(s,a) = R_{A,1}(s_1,a) + R_{A,2}(s_2,a)$;

• if $a \in A_1 {\setminus } A_2$, then $a \in A(s_1,s_2)$ if and only if $a \in A(s_1)$ with

  $$\begin{aligned} P(s,a)(s') = \left\{ \begin{array}{ll} P_1(s_1,a)(s_1') &{} \quad {if\,\,s_2=s_2'} \\ 0 &{} \quad {otherwise} \end{array} \right. \end{aligned}$$

  for all $s' = (s_1',s_2') \in S_1 \times S_2$ and $R_{A}(s,a) = R_{A,1}(s_1,a_1)$;

• if $a \in A_2 {\setminus } A_1$, then $a \in A(s_1,s_2)$ if and only if $a \in A(s_2)$ with

  $$\begin{aligned} P(s,a)(s') = \left\{ \begin{array}{ll} P_2(s_2,a)(s_2') &{} \quad {if\,\,s_1=s_1'} \\ 0 &{} \quad {otherwise} \end{array} \right. \end{aligned}$$

  for all $s' = (s_1',s_2') \in S_1 \times S_2$ and $R_{A}(s,a) = R_{A,2}(s_2,a_2)$;

• $R_{S}(s) = R_{S,1}(s_1) + R_{S,2}(s_2)$;

• $obs (s) = ( obs _1(s_1) , obs _2(s_2))$.

As is standard in CSP-style parallel composition (Roscoe 1997), an action which is in the action set of both components can only be performed when both components can perform it. Formally, using Definition 6, we see that, for any state $s=(s_1,s_2)$ of $\mathsf{M}_1 \Vert \mathsf{M}_2$, we have $A((s_1,s_2)) = (A(s_1) \cap A(s_2)) \cup (A(s_1) {\setminus } A_2) \cup (A(s_2 {\setminus } A_1)$. It therefore follows that, for any states $s, s'$ of $\mathsf{M}_1 \Vert \mathsf{M}_2$ with $obs (s)= obs (s')$, the available actions A(s) and $A(s')$ are identical, thus satisfying the condition imposed on a POMDP’s actions and observability in Definition 3.

In Definition 6 we have used addition to combine the reward values of the component POMDPs. However, depending on the system being modelled and its context, it may be more appropriate to combine the rewards in a different way, for example using multiplication or taking the maximum.

3 Verification and strategy synthesis for POMDPs

We now present our approach for verification and strategy synthesis for POMDPs.

3.1 Property specification

First, we define a temporal logic for the formal specification of quantitative properties of POMDPs. This is based on a subset (we omit temporal operator nesting) of the logic PCTL (Hansson and Jonsson 1994) and its reward-based extension in Forejt et al. (2011).

Definition 7

(POMDP property syntax) The syntax of our temporal logic for POMDPs is given by the grammar:

$$\begin{aligned} \phi&:\,:=&{\texttt {P}}_{\bowtie p}[\psi ] \mid {\texttt {R}}_{\bowtie q}[ \rho ] \\ \alpha&:\,:=&\texttt {true}\mid o \mid \lnot \alpha \mid {\alpha }{\wedge }{\alpha } \\ \psi&:\,:=&\alpha {\texttt {U}^{\leqslant k}\ }\alpha \mid \alpha {\texttt {U}\ }\alpha \\ \rho&:\,:=&\texttt {I}^{=k} \mid \texttt {C}^{\leqslant k} \mid \texttt {F}\ {\alpha } \end{aligned}$$

where o is an observation, ${\bowtie }\in \{\leqslant ,{<}, \geqslant ,{>}\}$, $p \in \mathbb {Q}\cap [0,1]$, $q\in \mathbb {Q}_{\geqslant 0}$ and $k \in \mathbb {N}$.

A POMDP property $\phi$ is an instance of either the probabilistic operator ${\texttt {P}}_{\bowtie p}[\cdot ]$ or the expected reward operator ${\texttt {R}}_{\bowtie q}[ \cdot ]$. Intuitively, a state satisfies a formula ${\texttt {P}}_{\bowtie p}[\psi ]$ if the probability of the path formula $\psi$ being satisfied is ${\bowtie } p$, and satisfies a formula ${\texttt {R}}_{\bowtie q}[\rho ]$ if the expected value of the reward formula $\rho$ is ${\bowtie } q$.

For path formulae, we allow time-bounded ($\alpha {\texttt {U}^{\leqslant k}\ }\alpha$) and unbounded ($\alpha {\texttt {U}\ }\alpha$) until formulae, and adopt the usual equivalences such as $\texttt {F}\ {\alpha } \equiv \texttt {true}{\texttt {U}\ }\alpha$ (“eventually $\alpha$”). For reward formulae, we allow $\texttt {I}^{=k}$ (state reward at k steps), $\texttt {C}^{\leqslant k}$ (reward accumulated over the first k steps) and $\texttt {F}\ {\alpha }$ (the reward accumulated until $\alpha$ becomes true). The propositional formulae ($\alpha$) are Boolean combinations of observations of the POMDP.

We have omitted nesting of ${\texttt {P}}$ and ${\texttt {R}}$ operators in Definition 7 to allow consistent property specification for either verification or strategy synthesis problems [the latter is considerably more difficult in the context of nested formulae (Baier et al. 2004; Brázdil et al. 2006)].

Definition 8

(POMDP property semantics) Let $\mathsf{M}=(S,{\bar{s}},A,P,R,\mathcal {O}, obs )$ be a POMDP. We define satisfaction of a property $\phi$ from Definition 7 with respect to a strategy ${\sigma }\in {\Sigma }_\mathsf{M}$ as follows:

$$\begin{aligned} \begin{array}{lll} \mathsf{M},{\sigma }{\,\models \,}{\texttt {P}}_{\bowtie p}[\,{\psi }\,] &{} \ \Leftrightarrow &{} { Pr _{\mathsf{M}}^{{\sigma }}}(\{\pi \in IPaths _{\mathsf{M}}\ |\ \pi {\,\models \,}\psi \}) \bowtie p \\ \mathsf{M},{\sigma }{\,\models \,}{\texttt {R}}_{\bowtie q}[{\rho }]&{} \ \Leftrightarrow \ &{} \mathbb {E}_{\mathsf{M}}^{{\sigma }}({ rew ^{}({\rho })})\bowtie q \\ \end{array} \end{aligned}$$

and, for any state $s \in S$ and path $\pi = s_0 \xrightarrow {a_0} s_1 \xrightarrow {a_1} \cdots \in IPaths _\mathsf{M}$:

$$\begin{aligned} \begin{array}{rcl} s {\,\models \,}\texttt {true}&{} &{} {\text{ always }} \\ s {\,\models \,}o &{} \;\; \Leftrightarrow \;\; &{} o \in obs (s) \\ s {\,\models \,}\lnot \alpha &{} \;\; \Leftrightarrow \;\; &{} s {\,\not \models \,}\alpha \\ s {\,\models \,}\alpha _1 \wedge \alpha _2 &{} \;\; \Leftrightarrow \;\; &{} s {\,\models \,}\alpha _1 \;\; \text{ and } \;\; s {\,\models \,}\alpha _2 \\ \pi {\,\models \,}\alpha _1 {\texttt {U}^{\leqslant k}\ }\alpha _2 &{} \;\; \Leftrightarrow \;\; &{} \exists i \in \mathbb {N}.\, (\, i\leqslant k \wedge s_i {\,\models \,}\alpha _2 \wedge \forall j {<} i .\, ( s_j {\,\models \,}\alpha _1) \,) \\ \pi {\,\models \,}\alpha _1 {\texttt {U}\ }\alpha _2 &{} \;\; \Leftrightarrow \;\; &{} \exists i \in \mathbb {N}.\, (\, s_i {\,\models \,}\alpha _2 \wedge \forall j {<} i .\, ( s_j {\,\models \,}\alpha _1) \,) \\ { rew ^{}({\texttt {I}^{= k}})}(\pi ) &{} \;\;= \;\; &{} R _S(s_{k}) \\ { rew ^{}({\texttt {C}^{\leqslant k}})}(\pi ) &{} \;\;= \;\; &{} \sum \limits _{j=0}^{k-1} \big ( R _S(s_j) + R _A(s_j,a_j) \big ) \\ { rew ^{}({\texttt {F}\ {\alpha }})}(\pi ) &{} \;\; = \;\; &{} \left\{ \begin{array}{ll} \infty &{} \quad {if } \forall j\in \mathbb {N} .\, s_j {\,\not \models \,}\alpha \\ \sum \limits _{j=0}^{m_\alpha -1} \big ( R _S(s_j) + R _A(s_j,a_j) \big ) &{} \quad {otherwise} \end{array} \right. \end{array} \end{aligned}$$

where $m_\alpha =\min \{j \mid s_j {\,\models \,}\alpha \}$.

3.2 Verification and strategy synthesis for POMDPs

Given a POMDP $\mathsf{M}$ and property $\phi$, we are interested in solving the dual problems of verification and strategy synthesis.

Definition 9

(POMDP verification) The verification problem for a POMDP $\mathsf{M}$ is: given a property $\phi$, decide if $\mathsf{M},{\sigma }{\,\models \,}\phi$ holds for all strategies ${\sigma }{\in }{\Sigma }_{\mathsf{M}}$.

Definition 10

(POMDP strategy synthesis) The strategy synthesis problem for a POMDP $\mathsf{M}$ is: given a property $\phi$, find, if it exists, a strategy ${\sigma }{\in }{\Sigma }_{\mathsf{M}}$ such that $\mathsf{M},{\sigma }{\,\models \,}\phi$.

The verification and strategy synthesis problems for a POMDP $\mathsf{M}$ and property $\phi$ can be solved similarly, by computing optimal values (i.e., minimum or maximum) for either path or reward objectives:

$$\begin{aligned} \begin{array}{lllllll} { Pr _{\mathsf{M}}^{\min }}(\psi ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \inf \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} { Pr _{\mathsf{M}}^{{\sigma }}}(\psi ) &{} &{} \mathbb {E}_{\mathsf{M}}^{\min }(\rho ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \inf \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} \mathbb {E}_{\mathsf{M}}^{{\sigma }}(\rho ) \\ { Pr _{\mathsf{M}}^{\max }}(\psi ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \sup \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} { Pr _{\mathsf{M}}^{{\sigma }}}(\psi ) &{}&{} \mathbb {E}_{\mathsf{M}}^{\max }(\rho ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \sup \nolimits _{{\sigma }\in {\Sigma }_\mathsf{M}} \mathbb {E}_{\mathsf{M}}^{{\sigma }}(\rho ) \end{array} \end{aligned}$$

and, where required, also synthesising an optimal strategy. For example, verifying $\phi = {\texttt {P}}_{\geqslant p}[\,{\psi }\,]$ requires computation of ${ Pr _{\mathsf{M}}^{\min }}(\psi )$ since $\phi$ is satisfied by all strategies if and only if $\smash {{ Pr _{\mathsf{M}}^{\min }}(\psi ) \geqslant p}$. Dually, consider synthesising a strategy for which $\phi ' = {\texttt {P}}_{< p}[\,{\psi }\,]$ holds. Such a strategy exists if and only if $\smash {{ Pr _{\mathsf{M}}^{\min }}(\psi ) {<} p}$ and, if it does, we can use a strategy that achieves a value less than p. A common practice in probabilistic verification is to simply query the optimal values directly, by omitting the bounds ${\bowtie } p$ (for ${\texttt {P}}$) or ${\bowtie } q$ (for ${\texttt {R}}$) using numerical properties.

Definition 11

(Numerical POMDP property) Let $\psi$ and $\rho$ be as specified in Definition 7. A numerical POMDP property is of the form ${\texttt {P}}_{\min =?}[\,{\psi }\,]$, ${\texttt {P}}_{\max =?}[\,{\psi }\,]$, ${\texttt {R}}_{\min =?}[{\rho }]$ or ${\texttt {R}}_{\max =?}[{\rho }]$ and yields the optimal value for the probability or reward formula.

As mentioned earlier, when solving a POMDP, we may only be able to under- and over-approximate optimal values, which requires adapting the processes sketched above. For example, if we have determined lower and upper bounds $\smash {p^\flat \leqslant { Pr _{\mathsf{M}}^{\min }}(\psi ) \leqslant p^\sharp }$. We can verify that $\phi = {\texttt {P}}_{\geqslant p}[\,{\psi }\,]$ holds for every strategy if $p^\flat \geqslant p$ or ascertain that $\phi$ does not hold if $p \geqslant p^\sharp$. But, if $p^\flat< p < p^\sharp$, we need to refine our approximation to produce tighter bounds. An analogous process can be followed for the case of strategy synthesis. The remainder of this section therefore focuses on how to (approximately) compute optimal values and strategies for POMDPs.

3.3 Numerical computation algorithms

Approximate numerical computation of either optimal probabilities ${ Pr _{\mathsf{M}}^{opt}}(\psi )$ or expected reward values $\mathbb {E}_{\mathsf{M}}^{opt}(\rho )$ on a POMDP $\mathsf{M}=(S,{\bar{s}},A,P,R,\mathcal {O}, obs )$ is performed with the sequence of steps given below, each of which is described in more detail subsequently. We compute both an under- and an over-approximation. For the former, we also generate a strategy which achieves this value.

• (A) We modify POMDP $\mathsf{M}$, reducing the problem to computing optimal values for a probabilistic reachability or expected cumulative reachability property;

• (B) We build and solve a finite abstraction of the (infinite-state) belief MDP ${\mathcal {B}}(\mathsf{M})$ yielding an over-approximation;

• (C) We synthesise and analyse a strategy for $\mathsf{M}$, giving an under-approximation;

• (D) If required, we refine the abstraction’s precision and repeat (B) and (C).

(A) Property reduction Checking ${\texttt {P}}_{\bowtie p}[\psi ]$ or ${\texttt {R}}_{\bowtie q}[ \rho ]$ properties of the logic from Definition 7 can always be reduced to checking either a probabilistic reachability (${\texttt {P}}_{\bowtie p}[{\texttt {F}\ }\alpha ]$) or expected cumulative reachability reward (${\texttt {R}}_{\bowtie q}[{\texttt {F}\ }\alpha ]$) property on a modified POMDP $\mathsf{M}'=(S',{\bar{s}}',A',P',R',\mathcal {O}', obs ')$. For the reduction in the case of MDPs, see for example Puterman et al. (1994).

(B) Over-approximation We solve the modified POMDP $\mathsf{M}'$. For simplicity, here and below, we describe the case of maximum reachability probabilities (the other cases are very similar) and thus need to compute $\smash {{ Pr _{\mathsf{M}'}^{\max }({\texttt {F}\ }O)}}$. We first compute an over-approximation, e.g., for maximum reachability probabilities $\smash {{ Pr _{\mathsf{M}'}^{\max }({\texttt {F}\ }O)}}$, we would find an upper bound. This is computed from an approximate solution to the belief MDP ${\mathcal {B}}(\mathsf{M}')$, whose construction we outlined in Sect. 2. This MDP has a continuous state space: the set of beliefs ${ Dist }(S')$, where $S'$ is the state space of $\mathsf{M}'$.

To approximate its solution, we adopt the approach of Yu (2006) and Yu and Bertsekas (2004) which computes values for a finite set of representative beliefs G whose convex hull is ${ Dist }(S')$. Value iteration is applied to the belief MDP, using the computed values for beliefs in G and interpolating to get values for those not in G. The resulting values give the required upper bound. We use Yu (2006) and Yu and Bertsekas (2004) as it works with unbounded (infinite horizon) and undiscounted properties. There are many other similar approaches (Shani et al. 2013), but these are formulated for discounted or finite-horizon properties.

The representative beliefs can be chosen in a variety of ways. We follow Lovejoy et al. (1991), where $\smash {G = \{ \frac{1}{M} v \, | \, v \in \mathbb {N}^{|S'|} \wedge \sum _{i=1}^{|S'|} v(i) = M \}} \subseteq { Dist }(S')$, i.e. a uniform grid with resolution M. A benefit is that interpolation is very efficient, using a process called triangulation (Eaves 1984). A downside is that the grid size is exponential in M. Efficiency might be improved with more complex grids that vary and adapt the resolution (Shani et al. 2013), but we found that Lovejoy et al. (1991) worked well enough for a prototype implementation.

(C) Under-approximation Since it is preferable to have two-sided bounds, we also compute an under-approximation: here, a lower bound on $\smash {{ Pr _{\mathsf{M}'}^{\max }({\texttt {F}\ }O)}}$. To do so, we first synthesise a finite-memory strategy $\sigma ^*$ for $\mathsf{M}'$ (which is often a required output anyway). The choices of this strategy are built by stepping through the belief MDP and, for the current belief, choosing an action that achieves the values returned by value iteration in (B) above—see for example Shani et al. (2013). We then compute, by building and solving the finite discrete-time Markov chain induced by $\mathsf{M}'$ and $\sigma ^*$, the value ${ Pr _{\mathsf{M}'}^{{\sigma }^*}({\texttt {F}\ }O)}$ which is a lower bound for $\smash {{ Pr _{\mathsf{M}'}^{\max }({\texttt {F}\ }O)}}$.

(D) Refinement Finally, when the computed approximations do not suffice to verify the required property (or, for strategy synthesis, ${\sigma }^*$ does not satisfy the property), we refine, by increasing the grid resolution M and repeating steps (B) and (C). We note that no a priori bound can be given on the error between the generated under- and over-approximations (recall that the basic problem is undecidable). Furthermore, just incrementing the resolution is not guaranteed to yield tighter bounds and in fact can yield worse bounds.

However, the abstraction approach that we use Yu (2006, Chap. 7), does provide an asymptotic guarantee on convergence. More precisely, convergence is shown for the case of expected total cumulative reward over models with non-negative rewards under the assumption that the cumulative reward is always finite. The case of probabilistic reachability can easily be reduced to the case of cumulative reward by assigning a one-off reward of 1 once the target is reached. For probabilistic reachability, finiteness of the cumulated reward is immediate. For expected cumulative reachability, reward finiteness is achieved by performing qualitative reachability analysis to remove states with infinite expected reward, i.e. the states that do not reach the target with probability 1. This is the standard approach for verifying MDPs against expected reachability properties (Forejt et al. 2011) and is decidable for POMDPs (Baier et al. 2008).

Example 2

We return to the maze example from Example 1 and Fig. 1. We can query the minimum expected number of steps to reach the target using the property ${\texttt {R}}_{\min =?}[{{\texttt {F}\ }o_ target }]$, where $o_ target$ is the distinct observation corresponding to the target location labelled ‘10’. Following the approach described above, we obtain a precise answer (the bounds are [4.300, 4.300]) for grid resolution $M=2$ (for which the number of points in the grid is 19) and are able to synthesise the optimal strategy described in Example 1.

We now increase the size of the maze by adding an additional location to the southern end of each of the three north-south alignments of locations (i.e., to the locations labelled ‘8’, ‘9’ and ‘10’) and keep the target as the southern most location of the middle such alignment. The resulting POMDP has 14 states and the same observation set as the original POMDP. Again considering the optimal expected number of steps to reach the target, we obtain the following results as the grid resolution is refined during the analysis:

• $M=2$ yields 34 grid points and the bounds $[4.3846,\infty ]$;

• $M=3$ yields 74 grid points and the bounds [4.8718, 5.3077];

• $M=4$ yields 150 grid points and the bounds [4.8846, 5.3077];

• $M=5$ yields 283 grid points and the bounds [5.0708, 5.3077];

• $M=6$ yields 501 grid points and the bounds [5.3077, 5.3077].

The $\infty$ value for the case when $M=2$ follows from the fact that the synthesised strategy does not reach the target with probability 1, and hence the expected reward for this strategy is infinite (see Definition 8). As can be seen, the under-approximation (the upper bound, here), obtained from the value of the synthesised strategy in step (C), yields the optimal value almost immediately, while the over-approximation (the lower bound), obtained from the approximate solution to the belief MDP in step (B), takes more time to converge to the optimal value.

The synthesised optimal strategy is essentially the same as the one for the maze of Fig. 1. For example, if the robot observes only walls on the east and west sides, then the strategy chooses to move the robot north until it reaches a location labelled either ‘0’, ‘2’ or ‘4’. Then it knows where the robot is and the strategy can easily determine an optimal route to the target.

4 Partially observable probabilistic timed automata

In this section, we define partially observable probabilistic timed automata (POPTAs), which generalise the existing model of probabilistic timed automata (PTAs) with the notion of partial observability from POMDPs explained in Sect. 2. We define the syntax of a POPTA, explain some syntactic restrictions that we impose and formally define the semantics, which is given by a POMDP parameterised by a time domain $\mathbb {T}$. We also present a notion of parallel composition for POPTAs and give several illustrative examples of the model. The section begins with some background on the simpler model of PTAs and the notions used to define them. For more detailed tutorial material on this topic, we refer the interested reader to Norman et al. (2013).

4.1 Time, clocks and clock constraints

Let $\mathbb {T}\in \{ \mathbb {R}, \mathbb {N}\}$ be the time domain of either the non-negative reals or naturals. As in classic timed automata (Alur and Dill 1994), we model real-time behaviour using non-negative, $\mathbb {T}$-valued variables called clocks, whose values increase at the same rate as real time. Assuming a finite set of clocks $\mathcal {X}$, a clock valuation v is a function $v: \mathcal {X}{{\rightarrow }} \mathbb {T}$ and we write $\mathbb {T}^\mathcal {X}$ for the set of all clock valuations over the time domain $\mathbb {T}$. Clock valuations obtained from v by incrementing all clocks by a delay $t \in \mathbb {T}$ and by resetting a set $X\subseteq \mathcal {X}$ of clocks to zero are denoted $v+t$ and $v[X:=0]$, respectively, and we write $\mathbf{0}$ if all clocks take the value 0. A (closed, diagonal-free) clock constraint $\zeta$ is either a conjunction of inequalities of the form $x \leqslant c$ or $x \geqslant c$, where $x \in \mathcal {X}$ and $c \in \mathbb {N}$, or $\texttt {true}$. We write $v \models \zeta$ if clock valuation v satisfies clock constraint $\zeta$ and use $CC ({\mathcal {X}})$ for the set of all clock constraints over $\mathcal {X}$.

4.2 Syntax of POPTAs

To explain the syntax of POPTAs, we first consider the simpler model of PTAs and then show how it extends to POPTAs.

Definition 12

(PTA syntax) A probabilistic timed automaton (PTA) is a tuple $\mathsf{P}= ( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r )$ where:

• $L$ is a finite set of locations and $\overline{l}\in L$ is an initial location;

• $\mathcal {X}$ is a finite set of clocks;

• $A$ is a finite set of actions;

• $inv : L {\rightarrow } CC ({\mathcal {X}})$ is an invariant condition;

• $enab : L \times A {\rightarrow } CC ({\mathcal {X}})$ is an enabling condition;

• $prob : L \times A {\rightarrow }{ Dist }(2^{\mathcal {X}} \times L )$ is a probabilistic transition function;

• $r = ( r _{ L }, r _{ A })$ is a reward structure where $r _{ L }: L \rightarrow \mathbb {R}$ is a location reward function and $r _{ A }: L \times A {\rightarrow }\mathbb {R}$ is an action reward function.

A state of a PTA is a pair (l, v) of location $l\in L$ and clock valuation $v\in \mathbb {T}^\mathcal {X}$. Time $t\in \mathbb {T}$ can elapse in the state only if the invariant $inv (l)$ remains continuously satisfied while time passes and the new state is then $(l,v+t)$, which we denote $(l,v)+t$. An action a is enabled in the state if v satisfies $enab (l,a)$ and, if it is taken, then the PTA moves to location $l'$ and resets the clocks $X\subseteq \mathcal {X}$ with probability $prob (l,a)(X,l')$. PTAs have two kinds of rewards:

• location rewards, which are accumulated at rate $r _{ L }(l)$ while in location l;

• action rewards $r _{ A }(l,a)$, which are accumulated when taking action a in location l.

PTAs equipped with such reward structures are a probabilistic extension of linearly-priced timed automata (Behrmann et al. 2001), also called weighted timed automata (Behrmann et al. 2001; Alur et al. 2004).

We now introduce POPTAs which extend PTAs by the inclusion of an observation function over locations.

Definition 13

(POPTA syntax) A partially observable PTA (POPTA) is a tuple $\mathsf{P}= ( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L , obs _ L )$ where:

• $( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r )$ is a PTA;

• $\mathcal {O}_ L$ is a finite set of observations;

• $obs _ L : L \rightarrow \mathcal {O}_ L$ is a location observation function.

For any locations $l,l' \in L$ with $obs _ L (l)= obs _ L (l')$, we require that $inv (l)= inv (l')$ and $enab (l,a)= enab (l',a)$ for all $a \in A$.

The final condition of Definition 13 ensures the semantics of a POPTA yields a valid POMDP: recall states with the same observation are required to have identical available actions. Like for POMDPs, for simplicity, we also assume that the initial location is observable, i.e., there exists ${\bar{o}}\in \mathcal {O}_ L$ such that $obs _ L (l)={\bar{o}}$ if and only if $l=\overline{l}$.

The observability of clocks The notion of observability for POPTAs is similar to the one for POMDPs, but applied to locations. Clocks, on the other hand, are always observable. The requirement that the same choices must be available in any observationally-equivalent states, implies the same delays must be available in observationally-equivalent states, and so unobservable clocks could not feature in invariant or enabling conditions. The inclusion of unobservable clocks would therefore necessitate modelling the system as a game with the elapse of time being under the control of a second (environment) player. The underlying semantic model would then be a partially observable stochastic game (POSG), rather than a POMDP. However, unlike POMDPs, limited progress has been made on efficient computational techniques for this model [belief space based techniques, for example, do not apply in general (Chatterjee and Doyen 2014)]. Even in the simpler case of non-probabilistic timed games, allowing unobservable clocks requires algorithmic analysis to restrict the class of strategies considered (Cassez et al. 2007; Finkbeiner and Peter 2012).

Encouragingly, however, we will later show in Sect. 6 that POPTAs with observable clocks were always sufficient for our modelling and analysis.

Restrictions on POPTAs At this point, we need to highlight a few syntactic restrictions on the POPTAs treated in this paper.

Assumption 1

For any POPTA $\mathsf{P}$, all clock constraints appearing in $\mathsf{P}$, i.e., in its invariants and enabling conditions, are required to be closed (no strict inequalities, e.g. $x{<}c$) and diagonal-free (no comparisons of clocks, e.g., $x{<}y$).

Assumption 2

For any POPTA $\mathsf{P}=( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L , obs _ L )$, resets can only be applied to clocks that are non-zero. More precisely, for any $l,l' \in L$, $a \in A$ and $X \subseteq \mathcal {X}$, if $prob (l,a)(X,l'){>}0$ then for any $v \in \mathbb {R}^\mathcal {X}$ such that $v(x)=0$ for some $x \in X$ we have either $v \not \models inv (l)$ or $v \not \models enab (l,a)$.

Assumption 1 is a standard restriction when using the digital clocks discretisation (Kwiatkowska et al. 2006) which we work with in this paper. The reasoning behind Assumption 2 is demonstrated in Example 4. Checking both assumptions can easily be done syntactically—see Sect. 5.

4.3 Semantics of POPTAs

We now formally define the semantics of a POPTA $\mathsf{P}$, which is given in terms of a POMDP. This extends the standard semantics of a PTA (Kwiatkowska et al. 2006) with the same notion of observability we gave in Sect. 2 for POMDPs. The semantics, $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}$, is parameterised by a time domain $\mathbb {T}$, giving the possible values taken by clocks. Before giving the semantics for POPTAs we consider the simpler case of PTAs.

Definition 14

(PTA semantics) Let $\mathsf{P}=( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r )$ be a probabilistic timed automaton. The semantics of $\mathsf{P}$ with respect to the time domain $\mathbb {T}$ is the MDP $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}=(S,{\bar{s}}, A \cup \mathbb {T},P,R)$ such that:

• $S = \{ (l,v) \in L \times \mathbb {T}^\mathcal {X}\mid v \models inv (l)\}$ and ${\bar{s}}= (\overline{l},\mathbf {0})$;

• for any $(l,v) \in S$ and $a \in A \cup \mathbb {T}$, we have $P((l,v),a) = \mu$ if and only if one of the following conditions hold:

  • (time transitions) $a \in \mathbb {T}$, $\mu = \delta _{(l,v + a)}$ and $v + a \models inv (l)$ for all $0 \leqslant t' \leqslant a$;

  • (action transition) $a \in A$, $v \models enab (l,a)$ and for $(l',v') \in S$:

    $$\begin{aligned} \begin{array}{c} \mu (l',v') = \sum \limits _{X \subseteq \mathcal {X}\wedge v' = v[X:=0]} prob (l,a)(X,l') \end{array} \end{aligned}$$

• for any $(l,v) \in S$ and $a \in A \cup \mathbb {T}$:

  $$\begin{aligned} R _S(l,v)= & {} r _{ L }(l) \\ R _A((l,v),a)= & {} \left\{ \begin{array}{ll} r _{ L }(l){\cdot }a &{}\quad if a \in {\mathbb {T}} \\ r _{ A }(l,a) &{}\quad {if a \in { A }.} \end{array} \right. \end{aligned}$$

For the standard (dense-time) semantics of a PTA, we take $\mathbb {T}=\mathbb {R}$. Since the semantics of a PTA is an infinite-state model, for algorithmic analysis, we first need to construct a finite representation. One approach for this is to use the digital clocks semantics for PTAs (Kwiatkowska et al. 2006) which generalises the approach for timed automata (Henzinger et al. 1992). This approach discretises a PTA model by transforming its real-valued clocks to clocks taking values from a bounded set of integers.

Before we give the definition we require the following notation. For any clock x of a PTA, let ${\mathbf {k}}_x$ denote the greatest constant to which x is compared in the clock constraints of the PTA. If the value of x exceeds ${\mathbf {k}}_x$, its exact value will not affect the satisfaction of any invariants or enabling conditions, and thus not affect the behaviour of the PTA.

Definition 15

(Digital clocks semantics) The digital clocks semantics of a PTA $\mathsf{P}$, written $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}$, can be obtained from Definition 14, taking $\mathbb {T}$ to be $\mathbb {N}$ and redefining the operation $v+t$ such that for any clock valuation $v\in \mathbb {N}^{{\mathcal {X}}}$, delay $t\in \mathbb {N}$ and clock $x \in {\mathcal {X}}$ we have $(v+t)(x) = \min \{ v(x) + t , {\mathbf {k}}_x+1 \}$.

We now extend Definition 14 and define the semantics of a POPTA.

Definition 16

(POPTA semantics) Let $\mathsf{P}=( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L ,$ $obs _ L )$ be a POPTA. The semantics of $\mathsf{P}$, with respect to the time domain $\mathbb {T}$, is the POMDP $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}=(S,{\bar{s}}, A \cup \mathbb {T},P,R,\mathcal {O}_ L \times \mathbb {T}^\mathcal {X}, obs )$ such that:

• $(S,{\bar{s}}, A \cup \mathbb {T},P,R)$ is the semantics of the PTA $( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r )$;

• for any $(l,v) \in S$, we have $obs (l,v)=( obs _ L (l),v)$.

As for PTAs, we consider both the ‘standard’ dense-time semantics and the digital clocks semantics of a POPTA, by taking $\mathbb {T}=\mathbb {R}$ and $\mathbb {T}=\mathbb {N}$ respectively. The fact that the digital clocks semantics of a POPTA is finite, and the dense-time semantics is generally uncountable, can be derived from the definitions. Under the restrictions on POPTAs described above, as we will demonstrate in Sect. 5, the digital semantics of a POPTA preserves the key properties required in this paper, namely optimal probabilities and expected cumulative rewards for reaching a specified observation set.

Time divergence As for PTAs and classic timed automata we restrict attention to time-divergent (or non-Zeno) strategies. Essentially this means that we restrict attention to strategies under which there are no unrealisable executions in which time does not advance beyond a certain point. There are syntactic and compositional conditions for PTAs for ensuring all strategies are time-divergent by construction (Norman et al. 2013). These are derived from analogous results on timed automata (Tripakis 1999; Tripakis et al. 2005) and carry over to our setting of POPTAs.

4.4 Parallel composition of POPTAs

As we did for POMDPs in Sect. 2, to aid the modelling of complex system, we now define a notion of parallel composition for POPTAs.

Definition 17

(Parallel composition of POPTAs) Consider any POPTAs $\mathsf{P}_i=( L _i, \overline{l}_i, \mathcal {X}_i, A _i , inv _i, enab _i, prob _i, r _i, \mathcal {O}_{ L ,i}, obs _{ L ,i})$ for $i \in \{1,2\}$ such that $\mathcal {X}_1 \cap \mathcal {X}_2 = \varnothing$. The parallel composition of $\mathsf{M}_1$ and $\mathsf{M}_2$, denoted $\mathsf{P}_1 \Vert \mathsf{P}_2$ is the POPTA:

$$\begin{aligned} \mathsf{P}_1 \Vert \mathsf{P}_2 \,{=}\, ( L _1 \times L _2, (\overline{l}_1,\overline{l}_2), \mathcal {X}_1 \cup \mathcal {X}_2, A _1 \cup A _2 , inv , enab , prob , r , \mathcal {O}_{ L ,1} \times \mathcal {O}_{ L ,2}, obs _ L ) \end{aligned}$$

where for any $l=(l_1,l_2)$, $l'=(l_1',l_2') \in L _1 \times L _2$, $a \in A _1 \cap A _2$, $a_1 \in A _1 {\setminus } A _2$, $a_2 \in A _2 {\setminus } A _1$ and $X \subseteq \mathcal {X}_1 \cup \mathcal {X}_2$:

$$\begin{aligned} inv (l)= & {} inv _1(l_1) \wedge inv _2(l_2) \\ enab (l,a)= & {} enab _1(l_1,a) \wedge enab _2(l_2,a) \\ enab (l,a_1)= & {} enab _1(l_1,a_1) \\ enab (l,a_2)= & {} enab _2(l_2,a_2) \\ prob (l,a)(X,l')= & {} prob _1(l_1,a)(X\cap \mathcal {X}_1 , l_1') {\cdot } prob _2(l_2,a)(X \cap \mathcal {X}_2,l_2') \\ prob (l,a_1)(X,l')= & {} \left\{ \begin{array}{ll} prob _1(l_1,a_1)(X,l_1') &{} \quad {if l_2=l_2' and X \subseteq \mathcal {X}_1} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \\ prob (l,a_2)(X,l')= & {} \left\{ \begin{array}{ll} prob _2(l_2,a_2)(X,l_2') &{} \quad {if l_1=l_1' and X \subseteq \mathcal {X}_2} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \\ r _{ A }(l,a)= & {} r _{ A ,1}(l_1,a) + r _{ A ,2}(l_2,a) \\ r _{ A }(l,a_1)= & {} r _{ A ,1}(l_1,a_1) \\ r _{ A }(l,a_2)= & {} r _{ A ,2}(l_2,a_2) \\ r _{ L }(l)= & {} r _{ L ,1}(l_1) + r _{ L ,2}(l_2) \\ obs _{ L }(l)= & {} ( obs _{ L ,1}(l_1) , obs _{ L ,2}(l_2)) . \end{aligned}$$

For POPTAs, it follows from Definitions 17 and 13 that, for any locations $l,l'$ of $\mathsf{P}_1 \Vert \mathsf{P}_2$ such that $obs _{ L }(l)= obs _{ L }(l')$ and action a of $\mathsf{P}_1 \Vert \mathsf{P}_2$ we have $inv (l)= inv (l')$ and $enab (l,a)= enab (l',a)$. In addition the following lemma holds.

Lemma 1

If $\mathsf{P}_1$ and $\mathsf{P}_2$ are POPTAs satisfying Assumptions 1 and 2, then $\mathsf{P}_1 \Vert \mathsf{P}_2$ satisfies Assumptions 1 and 2.

Proof

Consider any POPTAs $\mathsf{P}_1$ and $\mathsf{P}_2$ which satisfy Assumptions 1 and 2. Since the conjunction of closed and diagonal-free clock constraints are closed and diagonal-free, it follows that $\mathsf{P}_1 \Vert \mathsf{P}_2$ satisfies Assumption 1.

For Assumption 2, consider any locations $l=(l_1,l_2)$ and $l'=(l_1',l_2')$, action a, set of clocks X and clock valuation v of $\mathsf{P}_1 \Vert \mathsf{P}_2$ such that $prob (l,a)(X,l'){>}0$ and $v(x)=0$ for some clock $x \in X$. We have the following cases to consider.

• If $a \in A _1 \cap A _2$, then since $X \subseteq \mathcal {X}_1 \cup \mathcal {X}_2$ either $x \in \mathcal {X}_1$ or $x \in \mathcal {X}_2$. When $x \in \mathcal {X}_1$, since $\mathsf{P}_1$ satisfies Assumption 2, it follows that $v \not \models inv _1(l_1)$ or $v \not \models enab _1(l_1,a)$. On the other hand, when $x \in \mathcal {X}_2$, since $\mathsf{P}_2$ satisfies Assumption 2, it follows that $v \not \models inv _2(l_2)$ or $v \not \models enab _2(l_2,a)$. In either case, if follows from Definition 17 that $v \not \models inv (l)$ or $v \not \models enab (l,a)$.

• If $a \in A _1$, then by Definition 17 and since $prob (l,a)(X,l'){>}0$ we have $X \subseteq \mathcal {X}_1$ and $prob (l_1,a)(X,l_1'){>}0$. Therefore $x \in \mathcal {X}_1$ using the fact that $\mathsf{P}_1$ satisfies Assumption 2 it follows that $v \not \models inv _1(l_1)$ or $v \not \models enab _1(l_1,a)$. Again using Definition 17 it follows that $v \not \models inv (l)$ or $v \not \models enab (l,a)$.

• If $a \in A _2$, then using similar arguments to the case above and the fact $\mathsf{P}_2$ satisfies Assumption 2 we have $v \not \models inv (l)$ or $v \not \models enab (l,a)$.

Since these are all the cases to consider, it follows that $\mathsf{P}_1 \Vert \mathsf{P}_2$ satisfies Assumption 2 as required. $\square$

Similarly to POMDPs (see Sect. 2), the reward values of the component POPTAs can be combined using alternative arithmetic operators depending on the system under study. As for PTAs (Kwiatkowska et al. 2006), the semantics of the parallel composition of two POPTAs corresponds to the parallel composition of their individual semantic POMDPs using Definition 6. Formally, for POPTAs $\mathsf{P}_1,\mathsf{P}_2$ and time domain $\mathbb {T}$, we have that $[ \! [ {\mathsf{P}_1 \Vert \mathsf{P}_2} ] \! ]_\mathbb {T}= [ \! [ {\mathsf{P}_1} ] \! ]_\mathbb {T}\Vert [ \! [ {\mathsf{P}_2} ] \! ]_\mathbb {T}$.

Additional modelling constructs to aid higher level modelling for PTAs also carry over to the case of POPTAs. These include discrete variables, urgent and committed locations and urgent actions. For further details, see Norman et al. (2013).

4.5 Example POPTAs

Finally in this section, we present two example POPTAs. The second of these demonstrates why we have imposed Assumption 2 on POPTAs when using the digital clocks semantics.

Fig. 2

Example of a partially observable PTA (see Example 3)

Example 3

Consider the POPTA in Fig. 2 with clocks x, y. Locations are grouped according to their observations, and we omit enabling conditions equal to $\texttt {true}$. We aim to maximise the probability of eventually observing $o_5$. If the locations were fully observable, i.e. the model was a PTA, we would leave the initial location $\overline{l}$ when $x=y=1$ and then, depending on whether the random choice resulted in a transition to location $l_1$ or $l_2$, wait 0 or 1 time units, respectively, before leaving the location. This would allow us to move immediately from the locations $l_3$ or $l_4$ to the location $l_5$, meaning we eventually observe $o_5$ with probability 1. However, in the POPTA, we need to make the same choice in $l_1$ and $l_2$ since they yield the same observation. As a result, at most one of the transitions leaving locations $l_3$ and $l_4$ is enabled when reaching these locations (the transition from $l_3$ will be enabled if we wait 0 time units before leaving both $l_1$ and $l_2$, while the transition from $l_4$ will be enabled if we wait 1 time units before leaving both $l_1$ and $l_2$), and hence the maximum probability of eventually observing $o_5$ is 0.5.

Fig. 3

Example POPTA for only resetting non-zero clocks (see Example 4)

Example 4

The POPTA $\mathsf{P}$ in Fig. 3 demonstrates why our digital clocks approach (Theorem 1) is restricted to POPTAs which reset only non-zero clocks. We aim to minimise the expected reward accumulated before observing $o_3$ (the non-zero reward values are shown in Fig. 3). If the model was a PTA and locations were fully observable, the minimum reward would be 0, achieved by leaving the initial location $\overline{l}$ immediately and then choosing $a_1$ in location $l_1$ and $a_2$ in location $l_2$. However, in the POPTA model, if we leave $\overline{l}$ immediately, the locations $l_1$ and $l_2$ are indistinguishable (we observe $(o_{1,2},(0))$ when arriving in either), so we must choose the same action in these locations. Since we must leave the locations $l_1$ and $l_2$ when the clock x reaches the value 2, it follows that, when leaving the initial location immediately, the expected reward equals 0.5.

Now consider the strategy that waits $\varepsilon \in (0,1)$ before leaving the initial location $\overline{l}$, accumulating a reward of $\varepsilon$. Clearly, since $\varepsilon \in \mathbb {R}{\setminus } \mathbb {N}$, this is possible only in the dense-time semantics. We then observe either $(o_{1,2},(\varepsilon ))$ when entering the location $l_1$, or $(o_{1,2},(0))$ when entering the location $l_2$. Thus, observing whether the clock x was reset, allows a strategy to determine if the location reached is $l_1$ or $l_2$, and hence which of the actions $a_1$ or $a_2$ needs to be taken to observe $o_3$ without accumulating any additional reward. This yields a strategy that accumulates a total reward of $\varepsilon$ before observing $o_3$. Now, since $\varepsilon$ can be arbitrarily small, it follows that the minimum (infimum) expected reward for $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {R}$ is 0. On the other hand, for the digital clocks semantics, we can only choose a delay of 0 or 1 before leaving the initial location $\overline{l}$. In the former case, the expected reward is 0.5, as described above; for the latter case, we can again distinguish which of the locations $l_1$ or $l_2$ was reached by observing whether the clock x was reset. Hence, we can choose either $a_1$ or $a_2$ such that no further reward is accumulated, yielding a total expected reward of 1. Hence the minimum expected reward for $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}$ is 0.5, as opposed to 0 for $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {R}$.

5 Verification and strategy synthesis for POPTAs

We now present our approach for verification and strategy synthesis for POPTAs using the digital clock semantics given in the previous section.

5.1 Property specification

Quantitative properties of POPTAs are specified using the following logic.

Definition 18

(POPTA property syntax) The syntax of our logic for POPTAs is given by the grammar:

$$\begin{aligned} \begin{array}{rclrcl} \phi &{} :\,:= &{} {\texttt {P}}_{\bowtie p}[\psi ] \mid {\texttt {R}}_{\bowtie q}[ \rho ] &{} \\ \alpha &{} :\,:= &{} \texttt {true}\mid \zeta \mid o \mid \lnot \alpha \mid {\alpha }{\wedge }{\alpha } \\ \psi &{} :\,:= &{} \alpha {\texttt {U}^{\leqslant k}\ }\alpha \mid \alpha {\texttt {U}\ }\alpha \\ \rho &{} :\,:= &{} \texttt {I}^{=k} \mid \texttt {C}^{\leqslant k} \mid \texttt {F}\ {\alpha } \end{array} \end{aligned}$$

where $\zeta$ is a clock constraint, o is an observation, ${\bowtie }\in \{\leqslant ,{<}, \geqslant ,{>}\}$, $p \in \mathbb {Q}\cap [0,1]$, $q\in \mathbb {Q}_{\geqslant 0}$ and $k \in \mathbb {N}$.

This property specification language is similar to the one we proposed earlier for POMDPs (see Definition 7), but we allow clock constraints to be included in propositional formulae. However, as for PTAs (Norman et al. 2013), the bound k in path formulae ($\alpha {\texttt {U}^{\leqslant k}\ }\alpha$) and reward formulae ($\texttt {I}^{=k}$ and $\texttt {C}^{\leqslant k}$) corresponds to a time bound, as opposed to a bound on the number of discrete steps.

In the case of POPTAs, omitting the nesting of ${\texttt {P}}$ and ${\texttt {R}}$ operators is further motivated by the fact that the digital clocks approach is not applicable to nested properties (see Kwiatkowska et al. 2006 for details). Before we give the property semantics for POPTAs, we define the duration and position of a path in a POPTA.

Definition 19

(Duration of a POPTA path) For a POPTA $\mathsf{P}$, time domain $\mathbb {T}$, path $\pi = s_0 \xrightarrow {a_0} s_1 \xrightarrow {a_1} \cdots \in IPaths _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}$ and $i \in \mathbb {N}$, the duration of $\pi$ up to the $(i+1)$th state is given by:

$$\begin{aligned} \begin{array}{c} dur _\pi (i) = \sum \limits _{0 \leqslant j < i \wedge a_j \in \mathbb {T}} a_j . \end{array} \end{aligned}$$

Definition 20

(Position of a POPTA path) For a POPTA $\mathsf{P}$, time domain $\mathbb {T}$ and path $\pi = s_0 \xrightarrow {a_0} s_1 \xrightarrow {a_1} \cdots \in IPaths _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}$, a position of $\pi$ is a pair $(i,t) \in \mathbb {N}\times \mathbb {T}$ such that $t \leqslant dur _\pi (i+1) {-} dur _\pi (i)$. We say that position $(j,t')$ precedes position (i, t), written $(j,t') \prec (i,t)$, if $j{<}i$ or $j=i$ and $t'{<}t$.

Definition 21

(POPTA property semantics) Let $\mathsf{P}$ be a POPTA and $\mathbb {T}$ a time domain. We define satisfaction of a property $\phi$ from Definition 18 with respect to a strategy ${\sigma }\in {\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}$ as follows:

$$\begin{aligned} \begin{array}{lll} { [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T},{\sigma }{\,\models \,}{\texttt {P}}_{\bowtie p}[\,{\psi }\,] &{} \ \Leftrightarrow \ &{} { Pr _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}^{{\sigma }}}(\{\pi \in IPaths _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}\ |\ \pi {\,\models \,}\psi \}) \bowtie p \\ { [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T},{\sigma }{\,\models \,}{\texttt {R}}_{\bowtie q}[{\rho }]&{} \ \Leftrightarrow \ &{} \mathbb {E}_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}^{{\sigma }}({ rew ^{}({\rho })})\bowtie q \\ \end{array} \end{aligned}$$

and for any state $(l,v) \in L \times \mathbb {T}^\mathcal {X}$ and path $\pi = s_0 \xrightarrow {a_0} s_1 \xrightarrow {a_1} \cdots \in IPaths _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {T}}$:

$$\begin{aligned} \begin{array}{rcl} (l,v) {\,\models \,}\texttt {true}&{} &{} {\text{ always }} \\ (l,v) {\,\models \,}o &{} \;\; \Leftrightarrow \;\; &{} o \in obs _ L (l) \\ (l,v) {\,\models \,}\zeta &{} \;\; \Leftrightarrow \;\; &{} v {\,\models \,}\zeta \\ (l,v) {\,\models \,}\lnot \alpha &{} \;\; \Leftrightarrow \;\; &{} (l,v) {\,\not \models \,}\alpha \\ (l,v) {\,\models \,}\alpha _1 \wedge \alpha _2 &{} \;\; \Leftrightarrow \;\; &{} (l,v) {\,\models \,}\alpha _1 \; \; \text{ and } \; \; (l,v) {\,\models \,}\alpha _2 \\ \\ \pi {\,\models \,}\alpha _1 {\texttt {U}^{\leqslant k}\ }\alpha _2 &{} \;\; \Leftrightarrow \;\; &{} {there\,\,exists\,\,a\,\,position\,\,(i,t)\,\,of\,\,\pi \,\,such\,\,that\,\,\pi (i)+t\,\,{\,\models \,}\alpha _2,} \\ &{}&{} { dur _\pi (i)+t \leqslant k and \pi (j)+t' {\,\models \,}\alpha _1 {\vee } \alpha _2} \\ &{}&{} {for\,\,all\,\,positions\,\,(j,t')\,\,{\prec }\,\,(i,t)\,\,of\,\,\pi }\\ \pi {\,\models \,}\alpha _1 {\texttt {U}\ }\alpha _2 &{} \;\; \Leftrightarrow \;\; &{} {there\,\,exists\,\,a\,\,position\,\,(i,t)\,\,of\,\,\pi \,\,such\,\,that \,\,\pi (i)+t\,\,{\,\models \,}\,\,\alpha _2} \\ &{}&{} {and \pi (j)+t' {\,\models \,}\alpha _1 {\vee } \alpha _2\;for\;all\; positions\;(j,t') {\prec } (i,t) of \pi } \\ { rew ^{}({\texttt {I}^{= k}})}(\pi ) &{} \;\;= \;\; &{} R _S(s_{m_k}) \\ { rew ^{}({\texttt {C}^{\leqslant k}})}(\pi ) &{} \;\;= \;\; &{} \sum \limits _{j=0}^{m_k-1} R _A(s_j,a_j) + R _S(s_{m_k}) {\cdot } (k {-} dur _\pi (m_k)) \\ { rew ^{}({\texttt {F}\ {\alpha }})}(\pi ) &{} \;\; = \;\; &{} \left\{ \begin{array}{ll} \sum \limits _{j=0}^{m_\alpha -1} R _A(s_j,a_j) + R _S(s_{m_\alpha }) {\cdot } t_\alpha &{} \quad {if (m_\alpha ,t_\alpha )\;exists} \\ \infty &{} \quad {otherwise} \end{array} \right. \end{array} \end{aligned}$$

where $m_0 = 0$ and $m_k = \max \{ j \mid dur _\pi (i) {<} k \}$ if $k{>}0$ and, when it exists, $(m_\alpha ,t_\alpha )$ is is the minimum position of the path $\pi$ under the ordering $\prec$ for which $s_{m_\alpha }\!+t_\alpha {\,\models \,}\alpha$.

In the case of the until operator, as for timed automata (Henzinger et al. 1994), due to the dense nature of time we require that the disjunction $\alpha _1 \vee \alpha _2$, as opposed to the formula $\alpha _1$, holds at all positions preceding the first position at which $\alpha _2$ is satisfied.

For a POPTA $\mathsf{P}$ and time domain $\mathbb {T}$, the action rewards of $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}$ (see Definitions 16 and 14) encode both the accumulation of state rewards when a time transition is taken and the action rewards of $\mathsf{P}$. It follows that for cumulative reward properties, we only need to consider the action rewards of $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}$ together with the reward accumulated in the location we are in when either the time bound or the goal is first reached.

5.2 Verification and strategy synthesis

Given a POPTA $\mathsf{P}$ and property $\phi$, as for POMDPs we are interested in solving the dual problems of verification and strategy synthesis (see Definitions 9 and 10) for the ‘standard’ dense-time semantics of $\mathsf{P}$:

• decide if ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R},{\sigma }{\,\models \,}\phi$ holds for all strategies ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}$;

• find, if it exists, a strategy ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}$ such that ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R},{\sigma }{\,\models \,}\phi$.

Again, in similar fashion to POMDPs, these can be solved by computing optimal values for either path or reward objectives:

$$\begin{aligned} \begin{array}{rclcrcl} { Pr _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{\min }}(\psi ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \inf \nolimits _{{\sigma }\in {\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}} { Pr _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{{\sigma }}}(\psi ) &{}&{} \mathbb {E}_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{\min }(\rho ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \inf \nolimits _{{\sigma }\in {\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}} \mathbb {E}_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{{\sigma }}(\rho )\\ { Pr _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{\max }}(\psi ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \sup \nolimits _{{\sigma }\in {\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}} { Pr _{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{{\sigma }}}(\psi ) &{}&{} \mathbb {E}_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{\max }(\rho ) &{} \mathop {=}\limits ^{\mathrm{def}}&{} \sup \nolimits _{{\sigma }\in {\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}} \mathbb {E}_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}^{{\sigma }}(\rho ) \end{array} \end{aligned}$$

and, where required, also synthesising an optimal strategy. The remainder of this section therefore focuses on how to (approximately) compute optimal values and strategies for POPTAs.

5.3 Numerical computation algorithms

Approximate numerical computation of either optimal probabilities or expected reward values on a POPTA $\mathsf{P}$ is performed with the sequence of steps given below, As for POMDPs we compute both an under- and an over-approximation. For the former, we also generate a strategy which achieves this value.

• (A) We modify POPTA $\mathsf{P}$, reducing the problem to computing optimal values for a probabilistic reachability or expected cumulative reward property (Norman et al. 2013);

• (B) We apply the digital clocks discretisation of Sect. 4 to reduce the infinite-state semantics $[ \! [ {\mathsf{P}} ] \! ]_{\mathbb {R}}$ of $\mathsf{P}$ to a finite-state POMDP $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}$;

• (C) We build and solve a finite abstraction of the (infinite-state) belief MDP ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {N})$ of the POMDP from (B), yielding an over-approximation;

• (D) We synthesise and analyse a strategy for $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}$, giving an under-approximation;

• (E) If required, we refine the abstraction’s precision and repeat (C) and (D).

(A) Property reduction As discussed in Norman et al. (2013) (for PTAs), checking ${\texttt {P}}_{\bowtie p}[\psi ]$ or ${\texttt {R}}_{\bowtie q}[ \rho ]$ properties of the logic from Definition 18 can always be reduced to checking either a probabilistic reachability (${\texttt {P}}_{\bowtie p}[{\texttt {F}\ }\alpha ]$) or expected cumulative reachability reward (${\texttt {R}}_{\bowtie q}[{\texttt {F}\ }\alpha ]$) property on a modified model. For example, time-bounded probabilistic reachability (${\texttt {P}}_{\bowtie p}[{\texttt {F}^{\leqslant t}\ }\alpha ]$) can be transformed into probabilistic reachability (${\texttt {P}}_{\bowtie p}[{\texttt {F}\ }(\alpha \wedge y\leqslant t)]$) where y is a new clock added to $\mathsf{P}$ which is never reset and does not appear in any invariant or enabling conditions. We refer to Norman et al. (2013) for full details.

(B) Digital clocks Assuming the POPTA $\mathsf{P}$ satisfies Assumptions 1 and 2, we can construct a finite POMDP $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}$ representing $\mathsf{P}$ by treating clocks as bounded integer variables. The correctness of this reduction is demonstrated below. The translation itself is relatively straightforward, involving a syntactic translation of the PTA (to convert clocks), followed by a systematic exploration of its finite state space. At this point, we also syntactically check satisfaction of the restrictions (Assumptions 1 and 2) that we require of POPTAs.

(C–E) POMDP analysis This follows the approach for analysing probabilistic and expected cumulative reachability queries of POMDPs given in Sect. 3.

5.4 Correctness of the digital clocks reduction

We now prove that the digital clocks reduction preserves optimal probabilistic and expected reachability values of POPTAs. A direct corollary of this is that, for the logic presented in Definition 21, we can perform both verification and strategy synthesis using the finite-state digital clocks semantics.

Theorem 1

If $\mathsf{P}$ is a POPTA satisfying Assumptions 1 and 2, then, for any set of observations $O_ L$ of $\mathsf{P}$ and ${opt} \in \{\min ,\max \}$, we have:

$$\begin{aligned} { Pr _{ [ \! [ {\mathsf{P}} ] \! ]_{\mathbb {R}}}^{opt}({\texttt {F}\ }O_ L )} = { Pr _{ [ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}}^{opt}({\texttt {F}\ }O_ L )} \text{ and } {\mathbb {E}_{ [ \! [ {\mathsf{P}} ] \! ]_{\mathbb {R}}}^{opt}({\texttt {F}\ }O_ L )} = {\mathbb {E}_{ [ \! [ {\mathsf{P}} ] \! ]_\mathbb {N}}^{opt}({\texttt {F}\ }O_ L )}. \end{aligned}$$

Corollary 1

If $\mathsf{P}$ is a POPTA satisfying Assumptions 1 and 2, and $\phi$ is a property from Definition 18, then:

• ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R},{\sigma }{\,\models \,}\phi$ holds for all strategies ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}$ if and only if ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N},{\sigma }{\,\models \,}\phi$ holds for all strategies ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N}}$;

• there exists a strategy ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}$ such that ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R},{\sigma }{\,\models \,}\phi$ if and only if there exists a strategy ${\sigma }' {\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N}}$ such that ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N},{\sigma }'{\,\models \,}\phi$;

• if a strategy ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N}}$ is such that ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {N},{\sigma }{\,\models \,}\phi$, then ${\sigma }{\in }{\Sigma }_{{ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R}}$ and ${ [ \! [ {\mathsf{P}} ] \! ]}_\mathbb {R},{\sigma }{\,\models \,}\phi$.

Proof

In each case, the proof follows straightforwardly from Norman et al. (2013) which demonstrates that checking a property $\phi$ of the logic given in Definition 18 can always be reduced to checking either a probabilistic reachability (${\texttt {P}}_{\bowtie p}[{\texttt {F}\ }\alpha ]$) or expected cumulative reachability reward (${\texttt {R}}_{\bowtie q}[{\texttt {F}\ }\alpha ]$) property and using Theorem 1. The generalisation of results in Norman et al. (2013) from PTAs to POPTAs relies on the fact that propositional formulae $\alpha$ in the logic are based on either observations or clock valuations, both of which are observable. $\square$

Before we give the proof of Theorem 1 we require the following definitions and preliminary result. Consider a POPTA $\mathsf{P}=( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L , obs _ L )$. If $v,v'$ are clock valuations and X, Y sets of clocks such that $X {\ne } Y$ and $v(x){>}0$ for any $x \in X \cup Y$, then $v[X:=0] {\ne } v[Y:=0]$. Therefore, since we restrict our attention to POPTAs which reset only non-zero clocks (see Assumption 2), for a time domain $\mathbb {T}$, if there exists a transition from (l, v) to $(l',v')$ in $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}$, then there is a unique (possibly empty) set of clocks which are reset when this transition is taken. We formalise this through the following definition. For any clock valuations $v,v' \in \mathbb {T}^\mathcal {X}$, let:

$$\begin{aligned} X_{[v \mapsto v']} \mathop {=}\limits ^{\mathrm{def}}\{ x \in \mathcal {X}\mid v(x){>}0 \wedge v'(x)=0 \} . \end{aligned}$$

(1)

Using (1), the probabilistic transition function of $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}$ is such that, for any $(l,v) \in S$ and $a \in A$, we have $P((l,v),a) = \mu$ if and only if $v \models enab (l,a)$ and for any $(l',v') \in S$:

$$\begin{aligned} \mu (l',v') = \left\{ \begin{array}{ll} prob (l,a)(X_{[v \mapsto v']},l') &{} \quad {if\,v[X_{[v \mapsto v']}:=0]=v'} \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

We next introduce the concept of a belief PTA.

Definition 22

(Belief PTA) If $\mathsf{P}= ( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L , obs _ L )$ is a POPTA, the belief PTA of $\mathsf{P}$ is given by the tuple:

$$\begin{aligned} {\mathcal {B}}(\mathsf{P}) = \left( { Dist }( L , obs _ L ), \delta _{\overline{l}}, \mathcal {X}, A , inv ^{\mathcal {B}}, enab ^{\mathcal {B}}, prob ^{\mathcal {B}}, r ^{\mathcal {B}}\right) \end{aligned}$$

where:

• ${ Dist }( L , obs _ L )$ denotes the subset of ${ Dist }( L )$ where $\lambda \in { Dist }( L , obs _ L )$ if and only if, for $l,l' \in L$ such that $\lambda (l){>}0$ and $\lambda (l'){>}0$ we have $obs _ L (l)= obs _ L (l')$;

• the invariant condition $inv ^{\mathcal {B}}: { Dist }( L , obs _ L ) {{\rightarrow }} CC ({\mathcal {X}})$ and enabling condition $enab ^{\mathcal {B}}: { Dist }( L , obs _ L ) \times A {\rightarrow } CC ({\mathcal {X}})$ are such that, for $\lambda \in { Dist }( L , obs _ L )$ and $a \in A$, we have $inv ^{\mathcal {B}}(\lambda )= inv (l)$ and $enab ^{\mathcal {B}}(\lambda ,a)= enab (l,a)$ where $l \in L$ and $\lambda (l){>}0$;

• the probabilistic transition function:

  $$\begin{aligned} prob ^{\mathcal {B}}: { Dist }( L , obs _ L ) \times A {\rightarrow }{ Dist }(2^{\mathcal {X}} \times { Dist }( L , obs _ L )) \end{aligned}$$

  is such that, for any $\lambda ,\lambda ' \in { Dist }( L , obs _ L )$, $a \in A$ and $X \subseteq \mathcal {X}$ we have:

  $$\begin{aligned} \begin{array}{c} prob ^{\mathcal {B}}(\lambda ,a)(\lambda ',X) = \sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{o \in O \wedge \lambda ^{a,o,X} = \lambda '} \sum \limits _{l' \in L \wedge obs _ L (l')=o} \!\!\!\!\!\! prob (l,a)(l',X) \right) \end{array} \end{aligned}$$

  and, for any $l' \in L$:

  $$\begin{aligned} \lambda ^{a,o,X}(l') = \left\{ \begin{array}{ll} \frac{\sum _{l \in L } prob (l,a)(l',X) {\cdot } \lambda (l)}{\sum _{l \in L } \lambda (l) {\cdot } \left( \sum _{l^{{\scriptstyle \prime }} \in L \wedge obs _{{\scriptstyle L }}(l^{{\scriptstyle \prime }})=o} prob (l,a)(l',X) \right) } &{} \quad {if\, obs _ L (l')=o} \\ 0 &{} \quad \text{ otherwise; } \end{array} \right. \end{aligned}$$

• the reward structure $r ^{\mathcal {B}}= ( r _{ L }^{\mathcal {B}}, r _{ A }^{\mathcal {B}})$ consists of a location reward function $r _{ L }^{\mathcal {B}}: { Dist }( L , obs _ L ) {\rightarrow }\mathbb {R}$ and action reward function $r _{ A }^{\mathcal {B}}: { Dist }( L , obs _ L ) \times A \rightarrow \mathbb {R}$ such that, for any $\lambda \in { Dist }( L , obs _ L )$ and $a \in A$:

  $$\begin{aligned} \begin{array}{c} r _{ L }^{\mathcal {B}}(\lambda ) = \sum _{l \in L } \lambda (l) \cdot r _{ L }(l) \qquad \text{ and } \qquad r _{ A }^{\mathcal {B}}(\lambda ,a) = \sum _{l \in L } \lambda (l) \cdot r _A(l,a) . \end{array} \end{aligned}$$

For the above to be well defined, we require the conditions on the invariant condition and observation function given in Definition 13 to hold. For any $\lambda \in { Dist }( L , obs _ L )$, we let $o_\lambda$ be the unique observation such that $obs _ L (l)=o_\lambda$ and $\lambda (l){>}0$ for some $l \in L$.

We now show that, for a POPTA $\mathsf{P}$, the semantics of its belief PTA is isomorphic to the belief MDP of the semantics of $\mathsf{P}$.

Proposition 2

For any POPTA $\mathsf{P}$ satisfying Assumption 2, time domain $\mathbb {T}$ we have that the MDPs $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$ and ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ are isomorphic.

Proof

Consider any POPTA $\mathsf{P}=( L , \overline{l}, \mathcal {X}, A , inv , enab , prob , r , \mathcal {O}_ L , obs _ L )$ which satisfies Assumption 2, time domain $\mathbb {T}$ and let $[ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}= (S,{\bar{s}}, A \cup \mathbb {T},P,R)$. To show the MDPs $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$ and ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ are isomorphic we first give a bijection between their state spaces and then use this bijection to show that the probabilistic transition and reward functions of $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$ and ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ are isomorphic.

Considering the belief MDP ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$, see Definitions 5 and 16, and using the fact that $obs (l,v)=( obs _ L (l),v)$, for any belief states $b,b'$ and action a:

$$\begin{aligned} P^{\mathcal {B}}(b,a)(b') = \sum \limits _{\begin{array}{c} (o,v_o) \in O\times \mathbb {T}^\mathcal {X}\\ b^{a,(o,v_o)}=b' \end{array}}\sum \limits _{(l,v) \in S} b(l,v) \cdot \left( \sum \limits _{l' \in L \wedge obs _ L (l')=o} P((l,v),a)(l',v_o) \right) \end{aligned}$$

where, for any belief b, action a, observation $(o,v_o)$ and state $(l',v')$, we have $b^{a,(o,v_o)}(l',v')$ equals:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\sum _{(l,v) \in S} P((l,v),a)(l',v') \cdot b(l,v)}{\sum _{(l,v) \in S} b(l,v) \cdot \left( \sum _{l^{{\scriptstyle \prime \prime }} \in L \wedge obs _{{\scriptstyle L }}(l^{{\scriptstyle \prime \prime }})=o} P((l,v),a)(l'',v') \right) } &{} \quad {\mathrm{if}\, obs _ L (l')=o\,\,\mathrm{and}\,\,v'=v_o} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

(2)

and $R^{\mathcal {B}}(b,a) =\sum _{(l,v) \in S} R((l,v),a) \cdot b(l,v)$. Furthermore, by Definition 16 and since $\mathsf{P}$ satisfies Assumption 2, if $a \in A$:

$$\begin{aligned} P((l,v),a)(l',v')= & {} \left\{ \begin{array}{ll} prob (l,a)(X_{[v \mapsto v']},l') &{} \quad {\mathrm{if}\; v[X_{[v \mapsto v']}:=0]=v'} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

(3)

while if $a \in \mathbb {T}$:

$$\begin{aligned} P((l,v),a)(l',v')= & {} \left\{ \begin{array}{ll} 1 &{} \quad {\mathrm{if}\; l'=l and v' = v + a} \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

(4)

We see that $b^{a,(o,v_o)}(l',v')$ is zero if $v' {\ne } v_o$, and therefore we can write the belief as $(\lambda ,v_o)$ where $\lambda \in { Dist }( L )$ and $\lambda (l) = b^{a,(o,v_o)}(l,v_o)$ for all $l \in L$. In addition, for any $l' \in L$, if $\lambda (l'){>}0$, then $obs _ L (l')=o$. Since the initial belief ${\bar{b}}$ can be written as $(\delta _{\overline{l}},\mathbf {0})$ and we assume $obs _ L (\overline{l}) {\ne } obs _ L (l)$ for any $l {\ne } \overline{l}\in L$, it follows that we can write each belief b of ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ as a tuple $(\lambda ,v) \in { Dist }( L ) \times \mathbb {T}^\mathcal {X}$ such that for any $l,l' \in L$, if $\lambda (l){>}0$ and $\lambda (l'){>}0$, then $obs _ L (l)= obs _ L (l')$. Hence, it follows from Definitions 22 and 14 that there is a bijection between the states of ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ and the states of $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$.

We now use this bijection between the states to show that the probabilistic transition function and reward functions of $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$ and ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ are isomorphic. Using Definitions 5 and 16, for the probabilistic transition and the action reward functions we have the following two cases to consider.

• For any belief states $(\lambda ,v)$ and $(\lambda ',v')$ and action $a \in A$:

  $$\begin{aligned}&P^{\mathcal {B}}((\lambda ,v),a)(\lambda ',v')\\&\quad = \, \sum \limits _{\begin{array}{c} o \in \mathcal {O}_ L \\ \lambda ^{a,(o,v^{{\scriptstyle \prime }})}=\lambda ' \end{array}}\sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{\begin{array}{c} l' \in L \\ \mathcal {O}(l')=o \end{array}} P((l,v),a)(l',v') \right) \\&\quad = \, \sum \limits _{\begin{array}{c} o \in \mathcal {O}_ L \\ \lambda ^{a,(o,v^{{\scriptstyle \prime }})}=\lambda ' \end{array}}\sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{\begin{array}{c} l' \in L \\ \mathcal {O}(l')=o \end{array}} prob (l,a)(X_{[v \mapsto v']},l') \right) \qquad \text{ by } (3) \\&\quad = \, \sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{\begin{array}{c} o \in \mathcal {O}_ L \\ \lambda ^{a,(o,v^{{\scriptstyle \prime }})}=\lambda ' \end{array}} \sum \limits _{\begin{array}{c} l' \in L \\ \mathcal {O}(l')=o \end{array}} prob (l,a)(X_{[v \mapsto v']},l') \right) \qquad \text{ rearranging } \end{aligned}$$

  where for any $l' \in L$:

  $$\begin{aligned}&\lambda ^{a,(o,v')}(l') \\&\quad = \; \left\{ \begin{array}{ll} \frac{\sum _{l \in L } P((l,v),a)(l',v') \cdot \lambda (l)}{\sum _{l \in L } \lambda (l) \cdot \left( \sum _{l^{{\scriptstyle \prime \prime }} \in L \wedge obs _{{\scriptstyle L }}(l^{{\scriptstyle \prime \prime }})=o} P((l,v),a)(l'',v') \right) } &{} \quad {if\; obs _ L (l')=o} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \\&\quad = \; \left\{ \begin{array}{ll} \frac{\sum _{l \in L } prob (l,a)(X_{[v \mapsto v']},l') \cdot \lambda (l)}{\sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{l^{{\scriptstyle \prime \prime }} \in L \wedge obs _{{\scriptstyle L }}(l^{{\scriptstyle \prime \prime }})=o} prob (l,a)(X_{[v \mapsto v^{{\scriptstyle \prime }}]},l') \right) } &{} \quad {if\; obs _ L (l')=o} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \qquad \text{ by } (3)\\&\quad = \; \lambda ^{a,o,X_{[v \mapsto v']}} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text{ by } \text{ Definition }~(22). \end{aligned}$$

  Using this result, together with Definitions 22 and 14, it follows that the probabilistic transition functions are isomorphic in the case. For the action reward functions, we have:

  $$\begin{aligned} \begin{array}{c} R ^{\mathcal {B}}_A((\lambda ,v),a) = \sum \limits _{l\in L } r _ A (l,a) {\cdot } \lambda (l) \end{array} \end{aligned}$$

  which, again from Definitions 22 and 14, shows that the reward functions are isomorphic in this case.

• For any belief states $(\lambda ,v)$ and $(\lambda ',v')$ and time duration $t \in \mathbb {T}$:

  $$\begin{aligned} P^{\mathcal {B}}((\lambda ,v),t)(\lambda ',v')&= \; \left\{ \begin{array}{ll} \sum \limits _{l \in L } \lambda (l) \cdot P((l,v),a)(l,v') &{} \quad {if\; \lambda ^{t,(o_\lambda ,v')}=\lambda '} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

  where for any $l' \in L$:

  $$\begin{aligned} \lambda ^{t,(o_\lambda ,v')}(l')&= \left\{ \begin{array}{ll} \frac{\lambda (l')}{\sum \limits _{l \in L } \lambda (l)} &{} \quad {if\; v'=v + t} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \\&= \left\{ \begin{array}{ll} \lambda (l') &{} \quad {if \;v'=v + t} \\ 0 &{} \quad \text{ otherwise } \end{array} \right.&{\mathrm{since}\; \lambda \;\text {is a distribution}.} \end{aligned}$$

  Substituting this expression for $\lambda ^{t,(o_\lambda ,v')}$ into that of $P^{\mathcal {B}}((\lambda ,v),t)$ we have:

  $$\begin{aligned}&{P^{\mathcal {B}}((\lambda ,v),t)(\lambda ',v')} \\&\quad = \; \left\{ \begin{array}{ll} \sum \limits _{l \in L } \lambda (l) \cdot \left( \sum \limits _{l' \in L } P((l,v),a)(l',v') \right) &{} \quad \text{ if }\; \lambda =\lambda ' \;\mathrm{and}\; v'=v + t \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \\&\quad = \; \left\{ \begin{array}{ll} \sum \limits _{l \in L } \lambda (l) &{} \quad \text{ if }\; \lambda =\lambda '\; \mathrm{and}\; v'=v + t \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \qquad \text{ by }(4) \\&\quad = \; \left\{ \begin{array}{ll} 1 &{} \quad \text{ if }\; \lambda =\lambda '\; \mathrm{and}\; v'=v + t \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \qquad \text{ since } \;\lambda \; \text {is a distribution} \end{aligned}$$

  which, from Definitions 22 and 14, shows the probabilistic transition functions are isomorphic. For the action reward function of ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$, we have $R ^{\mathcal {B}}_A((\lambda ,v),t) = \sum _{l\in L } ( r _ L (l) {\cdot } t ) {\cdot } \lambda (l)$ and, from Definitions 22 and 14, this implies that the action reward functions are isomorphic.

Since these are the only cases to consider, both the probabilistic transition and action reward functions of ${\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ and $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}$ are isomorphic.

To complete the proof it remains to show that the state reward functions are isomorphic. Since, by Definition 5, for any belief state $(\lambda ,v)$, we have $R ^{\mathcal {B}}_S(\lambda ,v) = \sum _{l\in L } r _ L (l) {\cdot } \lambda (l)$, the result follows from Definitions 22 and 14. $\square$

We are now in a position to present the proof of Theorem 1.

Proof of Theorem 1

Consider any POPTA $\mathsf{P}$ satisfying Assumptions 1 and 2 and set of observables $O_ L$ of $\mathsf{P}$. Since the PTA ${\mathcal {B}}(\mathsf{P})$ satisfies Assumption 1, using results presented in Kwiatkowska et al. (2006), we have that:

$$\begin{aligned} { Pr _{ [ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {R}}^{opt}({\texttt {F}\ }T_{O_ L })}= & {} { Pr _{ [ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {N}}^{opt}({\texttt {F}\ }T_{O_ L })} \end{aligned}$$

(5)

$$\begin{aligned} {\mathbb {E}_{ [ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {R}}^{opt}({\texttt {F}\ }T_{O_ L })}= & {} {\mathbb {E}_{ [ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {N}}^{opt}({\texttt {F}\ }T_{O_ L })} \end{aligned}$$

(6)

for ${opt}\in \{\min ,\max \}$ and where $T_{O_ L } = \{ (l,v) \in L \times \mathbb {T}^\mathcal {X}\mid obs (l) \in O_ L \}$. Note that, although Kwiatkowska et al. (2006) considers only PTAs with a finite set of locations, the proofs corresponding to the above results do not rely this fact, and hence the results carry over to ${\mathcal {B}}(\mathsf{P})$ which has an uncountable number of locations.

Due to the relationship we have given between the optimal probabilistic and expected reachability values of a POMDP and its belief MDP (see Proposition 1), it follows that:

$$\begin{aligned} { Pr _{ [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}}^{{opt}}({\texttt {F}\ }O_ L )} = { Pr _{{\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})}^{{opt}}({\texttt {F}\ }T_{O_ L })} \text{ and } {\mathbb {E}_{ [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T}}^{{opt}}({\texttt {F}\ }O_ L )} = {\mathbb {E}_{{\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})}^{{opt}}({\texttt {F}\ }T_{O_ L })} . \end{aligned}$$

(7)

Using Proposition 2 and, since $\mathsf{P}$ satisfies Assumption 2, it follows therefore that $[ \! [ {{\mathcal {B}}(\mathsf{P})} ] \! ]_\mathbb {T}={\mathcal {B}}( [ \! [ {\mathsf{P}} ] \! ]_\mathbb {T})$ for $\mathbb {T}\in \{ \mathbb {R}, \mathbb {N}\}$. Combining this result with (5), (6) and (7), the theorem follows. $\square$

6 Implementation and case studies

We have built a prototype tool for verification and strategy synthesis of POMDPs and POPTAs as an extension of the PRISM model checker (Kwiatkowska et al. 2011; PRISM). Models are described in an extension of the existing PRISM modelling language, described in Sect. 6.1 below. For a specified POMDP or POPTA and property, the tool performs the steps outlined in Sects. 3 and 5, computing a pair of bounds for a given property and synthesising a corresponding strategy.

We have developed a number of POMDP and POPTA case studies, from a variety of different application domains, to evaluate the tool and techniques. In each case, partial observability, nondeterminism, probability and, in the case of POPTAs, real-time behaviour are all essential aspects required for the analysis. The case studies are described in detail in Sects. 6.2–6.7, and we summarise the experimental results from these examples in Sect. 6.8.

The software, details of all case studies, parameters and properties are available from www.prismmodelchecker.org/files/rts-poptas/. Also available through this link are the details for the POMDPs in Examples 1 and 2 and the POPTAs in Examples 3 and 4.

6.1 Modelling POMDPs and POPTAs in PRISM

Models in PRISM are specified in a high-level language based on guarded commands, which is a variant of Reactive Modules (Alur and Henzinger 1999). A model is constructed as a set of modules which can interact with each other. A module contains a number of finite-valued variables which define the module’s state. It’s behaviour is described by a set of guarded commands containing an (optional) action label, a guard and a probabilistic choice between updates:

$$\begin{aligned} \mathtt {[<\!\!action\!\!>]<\!\!guard\!\!> \; \rightarrow \;{<\!\!prob\!\!> \; : \;<\!\!update\!\!> \; + \; \cdots \; + \;<\!\!prob\!\!> \; : \; <\!\!update\!\!>};} \end{aligned}$$

A guard is a predicate over the variables of all modules and an update specifies, using primed variables, how the module’s own variables are updated. Interaction is both through the guards (guards can refer to variables of other modules) and the action labels (which allow modules to synchronise over commands). PRISM includes support for reward structures through reward items of the form:

$$\begin{aligned} \begin{array}{c} \texttt {{<}guard{>}\,:\,{<}reward{>};} \quad \text{ or } \quad \texttt {[{<}action{>}] \; {<}guard{>}\,:\,{<}reward{>};} \end{array} \end{aligned}$$

representing state and action rewards respectively. In the case of real-time models, modules can also contain $\texttt {clock}$ variables which can appear in guards and be reset by updates. In addition, the $\texttt {invariant}$ keyword is used to allow for the specification of location invariants.

We have extended the existing modelling language for MDPs and PTAs to allow specification of which variables are observables (the unspecified variables are considered hidden) through the keyword $\texttt {observables}$.

6.2 Wireless network scheduling

Our first case study is based on Yang et al. (2011) and concerns the wireless downlink scheduling of traffic to a number of different users with hard deadlines and where packets have priorities. The system is time-slotted: time is divided into periods and each period is divided into an equal number of slots. The system is parameterised by the total number of time periods (K) and the number of slots (T) per time period. At the start of each time period, a new packet is generated for each user with a priority assigned randomly. The goal of scheduling is to, in each period, deliver the packets to each user before the period ends. Packets not delivered by the end of a period are dropped.

There are c users and each one has a separate channel which can be in two states: one in which it is able to decode packets and one where it cannot. The state of each channel remains fixed within a time slot and between slots is Markovian, i.e., it changes randomly based only on the state in the previous slot. It is assumed that the conditions of the channels are unavailable to the system when scheduling packets. This corresponds to the real world situation where perfect channel information is not normally available since it requires non-negligible network resources.

Fig. 4

Initial fragment of the PRISM model for the network scheduling case study

Fig. 5

PRISM module for the scheduler in the network scheduling case study

The system is modelled in PRISM as a POMDP through the parallel composition of $3{\cdot }c+1$ modules (one module for the packet, priority and status of each channel and one module representing the scheduler). We show here the PRISM code for the case of $c=3$ users (and hence 3 channels). Figure 4 presents the first parts of the corresponding PRISM model. This defines the model type (POMDP), states which variables are observable and defines some constants used to describe the model. All variables except those representing the status of the channels are defined as observable, and hence the scheduler can observe the elapsed time, which packets need to be sent and their priorities. The constants include the numbers of time periods (K), of slots per period (T), and the probabilities that the channels change state after each time slot.

The module for the scheduler is presented in Fig. 5. The scheduler has two local states: in the first (when $sched =0$), it updates the timing variables, i.e., either moves to the next slot or to the next period; in the second local state (when $sched =1$), it decides which packet to schedule for delivery in the current time slot by (nondeterministically) selecting one of the actions $send1$, $send2$ and $send3$ corresponding to the three channels. The scheduler can also choose not to try and send a packet by instead choosing the action $idle$.

Fig. 6

PRISM modules for the channels in the network scheduling case study

The modules for the channels are presented in Fig. 6. Each channel has three modules representing:

• if the packet for the current time period has been sent;

• the priority of the current packet to be sent;

• the status of the channel.

As can be seen in Fig. 6, we only give the full specification of the modules for the first channel; the modules for the remaining channels are defined through renaming. In the module $packet1$, commands labelled by the action $send1$ are only enabled when $pack1 =1$, and hence, as the modules synchronise, the scheduler can only choose to send a packet if it has not yet been delivered. This module also specifies that, if a packet is sent and the channel is down ($chan1 =0$), the packet does not get delivered and still needs to be sent. In the modules $packet1$ and $priority1$, we can see that at the start of each period there is a new packet to send on each channel and the priority of these packets is chosen at random. The module $channel1$ specifies that in the initial state the status of the channel is selected uniformly at random and after this the status of the channel follows the probabilities given in Fig. 4.

Finally, the reward structures for the model are presented in Fig. 7. The first reward structure is used to count the number of dropped packets, i.e., the number of packets that remain to be sent at the end of each period. This is achieved by counting the number of the variables $pack1$, $pack2$ and $pack3$ that equal 1 when a time period ends. The second reward structure is used to accumulate the priorities of delivered packets, and therefore each time a packet gets delivered we assign an action reward equal to the corresponding priority.

Fig. 7

PRISM specification of reward structures for the network scheduling case study

For this case study, we synthesise strategies that maximise the expected cumulative reward based on the priorities of the packets using the reward structure of Yang et al. (2011) and, for a simpler model where the priorities of packets are not considered (by removing the modules $priority1$, $priority2$ and $priority3$ and related reward structure), that minimise the expected number of dropped packets. These requirements can be specified in PRISM as follows:

• $\texttt {R}\{{``} priority {''}\}\texttt {max}=?[\texttt {F} \; ( sched =0 \; \& \; t = T {-}1 \; \& \; k = K {-}1) \; ]$;

• $\texttt {R}\{{``} dropped\_packets {''}\}\texttt {min}=?[\texttt {F} \; ( sched =0 \; \& \; t = T {-}1 \; \& \; k = K {-}1) \; ]$.

In Yang et al. (2011) the analysis is through handwritten proofs while here we construct a formal model and perform automated analysis, in addition in Yang et al. (2011) discounted objectives are considered while we analyse undiscounted reachability objectives.

In Yang et al. (2011) it is demonstrated that, due to hard deadlines and unknown channel status, idling, i.e. not sending a packet in certain slots even when there is a packet to send, is the optimal choice in certain situations. The reasoning given is that this allows the scheduler to learn the status of the channels and then improve the success of future transmissions of packets. Our analysis confirms this to be the case when priorities are considered. For example, when $T=3$ and $K=2$ which are the parameter values (Yang et al. 2011) use, we find that disallowing the scheduler to idle causes the maximum expected accumulated reward interval to decrease from [36.322, 36.324] to [36.316, 36.318] when the grid resolution is 48.

Our results also demonstrate that, when priorities of packets are not considered, idling is not an optimal choice. By using the presented approach this analysis was easy to perform as we only needed to make a simple change to the PRISM model removing the option for the scheduler to idle unless all packets in the current slot have been delivered, i.e. in the module for the scheduler (see Fig. 5) the command labelled by the action $idle$ becomes:

$$ \begin{aligned} \begin{array}{c} \quad [ idle ] sched =1 \; \& \; pack1 =0 \; \& \; pack2 =0 \; \& \; pack3 =0 \; \rightarrow \; ( sched' =0); \end{array} \end{aligned}$$

Fig. 8

Processor task graph for computing $D \times (C \times (A + B)) + ((A+B)+(C \times D))$

6.3 Task-graph scheduler

Next, we consider a task-graph scheduling problem adapted from Bouyer et al. (2011), where the goal is to minimise the time or energy consumption required to evaluate the arithmetic expression $D \times (C \times (A + B)) + ((A+B)+(C \times D))$ using two processors ($P_1$ and $P_2$) that have different speed and energy requirements. Figure 8 presents a task graph for this computation showing the tasks that need to be performed and the dependencies between the tasks. The specification of the processors, as given in Bouyer et al. (2011), is as follows:

• time for addition 2 and 5 picoseconds for processors $P_1$ and $P_2$;

• time for multiplication 3 and 7 picoseconds for processors $P_1$ and $P_2$;

• idle energy usage 10 and 20 Watts for processors $P_1$ and $P_2$;

• active energy usage 90 and 30 Watts for processors $P_1$ and $P_2$.

The system is formed as the parallel composition of three timed automata: one for each processor and one for the scheduler. In Fig. 9 we give the timed automaton representing $P_1$. The labels $p1\!\_add$ and $p1\!\_ mult$ on the transitions represent an addition and multiplication task being scheduled on $P_1$ respectively, while the label $p1\!\_done$ indicates that the current task has been completed. The timed automaton includes the clock $x_1$ which is used to keep track of the time that a task has been running. It is reset when a task starts and the invariants and guards correspond to the time required to complete the tasks of addition and multiplication for $P_1$. The reward structure for computing the expected energy consumption associates a reward of 10 with the $stdby$ location and reward 90 with the locations $add$ and $mult$ (corresponding to the energy usage of process $P_1$ when idle and active respectively) and all action rewards are 0.

The timed automaton and reward structure for processor $P_2$ are similar except that the names of the labels, invariants, guards and reward values correspond to the specification of $P_2$. The automata for the scheduler keeps track of the tasks that have been completed and nondeterministically decides how tasks get allocated to processes, subject to meeting the dependencies between tasks. After forming the parallel composition, the reward structure for the expected energy consumption then includes the addition of the reward structures for energy consumption of $P_1$ and $P_2$. The reward structure for computing the expected time associates a reward of 1 with all locations of the composed system.

Fig. 9

Original timed automaton of processor $P_1$ from Bouyer et al. (2011)

Fig. 10

POPTA of processor $P_1$ with a low power state

We extend both the basic model of Bouyer et al. (2011) described above and the extension from Norman et al. (2013) which uses PTAs to model probabilistic task execution times. In both models we extend the processor $P_1$ with a new ‘low power’ state allowing it to save energy when not in use, but which incurs a delay of 4 picoseconds when waking up to execute a new task. This state is entered with probability $sleep$ after each task is completed. We assume that the scheduler cannot observe whether the processor enters this lower power state, and hence the model is a POPTA. The POPTA for $P_1$ including this lower power state (labelled $low$) is given in Fig. 10. We model the scheduler inability to observe if the processor is in the standby or lower power state by assigning the same observation ($o_{idle}$) to the locations labelled $stdby$ and $low$. To model the 4 picosecond delay when waking from the low power state, we introduce the locations $wake _1$ and $wake _2$ corresponding to waking up to perform an add and a multiplication operation respectively. Not included in Fig. 10 is the initial location, from which we immediately move, by adding the guard $x=0$ to this location, to either the location $low$ or $stby$ each with probability 0.5. The PRISM module representing $P_1$ is given in Fig. 11 with the variable $sleep1$ specified as unobservable. The PTA model with probabilistic task execution times given in Norman et al. (2013) can be extended similarly. For both models, we generate optimal schedulers (minimising expected execution time or energy usage) using strategy synthesis.

Fig. 11

PRISM module of processor $P_1$ with a low power state

6.4 The NRL pump

The NRL (Naval Research Laboratory) pump (Kang et al. 1998) is designed to provide reliable and secure communication over networks of nodes with ‘high’ and ‘low’ security levels. It prevents a covert channel leaking information from ‘high’ to ‘low’ through the timing of messages and acknowledgements. Communication is buffered and probabilistic delays are added to acknowledgements from ‘high’ in such a way that the potential for information leakage is minimised, while maintaining network performance. A PTA model is considered in Lanotte et al. (2014).

We model the pump as a POPTA using a hidden variable for a secret value $z\in \{0,1\}$ (initially set uniformly at random) which ‘high’ tries to covertly communicate to ‘low’. The model is the parallel composition of three POPTAs representing ‘high’, ‘low’ and the pump. This communication is attempted by adding a delay of $h_0$ or $h_1$, depending on the value of z, whenever sending an acknowledgement to ‘low’. In the model, ‘low’ sends N messages to ‘high’ and tries to guess z based on the time taken for its messages to be acknowledged. We consider the maximum probability ‘low’ can (either eventually or within some time frame) correctly guess z. We also study the expected time to send all messages and acknowledgements. These properties measure the security and performance aspects of the pump. Results are presented in Fig. 12 varying $h_1$ and N (we fix $h_0=2$). They show that increasing either the difference between $h_0$ and $h_1$ (i.e., increasing $h_1$) or the number N of messages sent improve the chance of ‘low’ correctly guessing the secret z, at the cost of a decrease in network performance. On the other hand, when $h_0=h_1$, however many messages are sent, ‘low’, as expected, learns nothing of the value being sent and at best can guess correctly with probability 0.5.

Fig. 12

Analysing security/performance of the NRL pump: a maximum probability of covert channel success; b maximum expected transmission time

6.5 Non-repudiation protocol

The next case study is a non-repudiation protocol for information transfer due to Markowitch and Roggeman  (1999). It is designed to allow an originator O to send information to a recipient R while guaranteeing non-repudiation, that is, neither party can deny having participated in the information transfer. The initialisation step of the protocol requires O to randomly select an integer N in the range $1,\dots ,K$ that is never revealed to R during execution.

In previous analyses (Lanotte et al. 2005; Norman et al. 2013), modelling this step was not possible since no notion of (non-)observability was used. We resolve this by building a POPTA model of the protocol including this step, thus matching Markowitch and Roggeman’s original specification. In particular, we include a hidden variable to store the random value N. The model is the parallel composition of two component POPTAs representing the originator and the recipient.

We build two POPTA models: a basic model, where R’s only malicious behaviour corresponds to stopping early; and a more complex model, where R also has access to a decoder. We also consider a simpler discrete-time POMDP model where the timing information is abstracted and R’s only malicious behaviour corresponds to stopping early. We compute the maximum probability that R gains an unfair advantage (obtains the information from O while being able to deny participating). Our results (see Tables 1, 2) show that, for the basic models, this probability equals 1 / K when convergence is achieved and that R is more powerful in the complex model.

6.6 The dining cryptographers protocol

This protocol, due to Chaum  (1988), solves the following problem. A group of N cryptographers are having dinner at their favourite restaurant. The waiter informs them that arrangements have been made for the bill to be paid anonymously: one of the cryptographers might be paying for the dinner, or it might be their master. The cryptographers respect each other’s privacy, but would like to know if the master is paying for dinner. The protocol proceeds as follows.

Table 1 Experimental results from verification/strategy synthesis of POMDPs

Table 2 Experimental results from verification/strategy synthesis of POPTAs

• Each cryptographer flips an unbiased coin and only informs the cryptographer on the right of the outcome.

• Each cryptographer states whether the two coins that it can see (the one it flipped and the one the left-hand neighbour flipped) are the same (‘agree’) or different (‘disagree’). However, if a cryptographer actually paid for dinner, then the cryptographer instead states the opposite (‘disagree’ if the coins are the same and ‘agree’ if the coins are different).

An even number of ‘agrees’ indicates the master paid, an odd number that a cryptographer paid. But this provides no additional information as to which cryptographer actually paid.

We model the protocol as a parallel composition of POMDPs: one for each cryptographer and one representing the master. The observable behaviour of the POMDP is with respect to a specific cryptographer. In particular, all the ‘agree’ and ‘disagree’ announcements are visible to this cryptographer, but only the values of its own and its left-hand neighbour’s coins are visible.

In the model we do not impose any requirement on the ordering in which the cryptographers state ‘agree’ or ‘disagree’, in case this can be used to provide information to the specific cryptographer as to who actually pays. In the initialisation phase, we assume that the master selects, uniformly at random, one of the other cryptographers to pay.

We analyse both the minimum and maximum probability that the specified cryptographer can guess which of the other cryptographers actually pays. We find that, when the approach converges, the maximum probability that the cryptographer can correctly guess which of the other cryptographers pays is the same both before and after the protocol is run, i.e., by selecting one of the other cryptographers uniformly at random. Hence we have demonstrated that the protocol does indeed satisfy the privacy requirement in these cases. Privacy had previously been analysed with PRISM using MDPs (see PRISM), however in this work an exponential number of properties needed to be verified, as opposed to the single maximum probabilistic reachability property required when modelling the protocol as a POMDP.

6.7 Grid-world robot

The final case study is based on the POMDP example given in Littman et al. (1995). There is a robot placed randomly an $n \times n$ grid and its goal is to reach the south east corner location. All locations of the grid look identical, i.e., have the same observation, except the target. The robot can perform four different actions corresponding to moving in the four compass directions. There is no change in location if the chosen action would take the robot off the grid. We have constructed POMDP models for the cases when n equals 3 and 4. For both models we have synthesised a controller that optimises (i.e., minimises) the expected number of steps to reach the target and a controller that optimises (i.e., maximises) the probability of reaching the target within k steps.

6.8 Experimental results

Tables 1 and 2 summarise a representative set of experimental results from the analysis of the POMDP and POPTA case studies, respectively. All were run on a 2.8 GHz PC with 8GB RAM. The table shows the parameters used for each model (see www.prismmodelchecker.org/files/rts-poptas/ for details), the property analysed and various statistics from the analysis: the size of the POMDP (in the case of POPTAs this is the POMDP that is obtained through the digital clocks semantics); number of observations; number of hidden values (i.e., the maximum number of states with the same observation); the grid size (resolution M and total number of points); the time taken; and the results obtained. For comparison, in the rightmost column, we show what result is obtained if the POMDP or POPTA is treated as an MDP or PTA (by making everything observable).

On the whole, we find that the performance of our prototype is good, especially considering the complexity of the POMDP solution methods and the fact that we use a relatively simple grid mechanism. We are able to analyse POPTAs whose integer semantics yields POMDPs of up to 60,000 states, with experiments usually taking just a few seconds and, at worst, 20 minutes. These are, of course, smaller than the standard PTA or MDP models that can be verified, but we were still able to obtain useful results for several case studies.

The values in the rightmost column of Tables 1 and 2 illustrate that the results obtained with POMDPs and POPTAs would not have been possible using an MDP or PTA model, i.e., where all states of the model are observable. In the $wireless\;network$ case study in the MDP model the scheduler can see the status of the channels, and hence use this information to decrease the number of dropped packets and increase the cumulate reward based on the priorities of packets. In the $crypt$ and $pump$ case studies, the MDP and PTA give probability 1 of guessing correctly (e.g., in the $pump$ example, ‘low’ can simply read the value of the secret). Similarly, for the nrp models, the PTA gives probability 1 of unfairness because the recipient can read the random value the originator selects. For the $scheduler$ example, the PTA model gives a scheduler with better time/energy consumption but which cannot be implemented in practice since the power state is not visible. In similar fashion, for the $grid$ example, we see that optimal strategy is improved if the precise location on the grid is available.

Another positive aspect is that, in many cases, the bounds generated are very close (or even equal, in which case the results are exact). For the $pump$ and $scheduler$ case studies, we included results for the smallest grid resolution M required to ensure the difference between the bounds is at most 0.001. In many cases, this is achieved with relatively small values (for the $scheduler$ case study, in particular, M is at most 4). For the cases we were unable to do this we have instead included the results for the largest grid resolution for which POMDP solution was possible: higher values could not be handled within the memory constraints of our test machine. We anticipate being able to improve this in the future by adapting more advanced approximation methods for POMDPs (Shani et al. 2013). For the $crypt$ case study, as we increase the number of cryptographers, we find that the over approximations obtained through the approximate solution of the belief MDP are coarse (0.0 and 1.0 for minimum and maximum probabilities, respectively) while the under approximations obtained through synthesis are precise. This appears to be the due to large number of hidden values in the POMDP compared to the other case studies and our prototype implementation using only a basic approximation method.

7 Conclusions

We have proposed novel methods for the verification and control of partially observable, probabilistic systems for both discrete and dense models of time. We have used temporal logics to define probabilistic, timed properties and reward measures. For discrete-time models, the techniques developed are based on a belief space approximation. For dense-time models we have demonstrated that the digital clocks discretisation preserves the properties of interest, which allows us to employ the techniques developed for the discrete-time case. We have implemented this work in an extension of the probabilistic model checker PRISM and demonstrated the effectiveness on several case studies.

Future directions include more efficient approximation schemes, zone-based implementations and development of the theory for unobservable clocks. Allowing unobservable clocks, as mentioned previously, will require moving to partially observable stochastic games and restricting the class of strategies.

Appendix: Construction of the belief MDP

For the convenience of the reader, we have included below, the construction of the belief MDP for a POMDP $\mathsf{M}= (S,{\bar{s}},A,P, R ,\mathcal {O}, obs )$ (see Definition 5). We use the standard notation from the POMDP literature, for example $\mathbf {Pr}[ \, s' ,a,b \, ]$ denotes the probability that the next state is $s'$, the action a is performed and the current belief is b and $\mathbf {Pr}[\, o \, | \, a,b \, ]$ denote the probability of observing o conditioned on the action being a is performed and that the current belief state is b.

First, let us suppose we are in a belief state b, perform action a and observe o. Based on this new information we move to a new belief state $b^{a,o}$ using the observation function of $\mathsf{M}$. Let us now construct this new belief state. First, by construction, we have for any $s' \in S$:

$$\begin{aligned} b^{a,o}(s')&= \; \mathbf {Pr}[\, s' \, | \, o,a,b \, ] \\&= \frac{\mathbf {Pr}[ \, s' ,o,a,b \, ]}{\mathbf {Pr}[ \, o,a,b \, ]}&\text{ by } \text{ definition } \text{ of } \text{ conditional } \text{ probabilities } \\&= \; \left\{ \begin{array}{ll} \dfrac{\mathbf {Pr}[ \, s' ,a,b \, ]}{\mathbf {Pr}[ \, o,a,b \, ]} &{}\quad {\mathrm{if}\,\, obs (s')=o} \\ 0 &{} \quad \text{ otherwise } \end{array} \right. \!\!\!\!\!\!\!\!\!\!&\text{ by } \text{ definition } \text{ of } obs \text{. } \end{aligned}$$

Now considering the numerator in the first case, since the value of $s'$ is dependent on the other values:

$$\begin{aligned} \mathbf {Pr}[ \, s' ,a,b \, ]&= \; \mathbf {Pr}[ \, s' \, | \, a,b \, ]\cdot \mathbf {Pr}[ \, a,b \, ] \\&= \; \mathbf {Pr}[ \, s' \, | \, a,b \, ]\cdot 1&\text{ since } \text{ b } \text{ and } \text{ a } \text{ are } \text{ fixed } \\&= \; {\sum _{s \in S}} \mathbf {Pr}[ \, s' \, | \, a,s \, ] \cdot b(s)&\text{ definition } \text{ of } \,\,b \\&= \; {\sum _{s \in S}} P(s,a)(s') \cdot b(s)&\text{ definition } \text{ of } \,\,P. \end{aligned}$$

For the denominator since o is dependent on b and a we have:

$$\begin{aligned} \mathbf {Pr}[ \, o,a,b \, ]&= \; \mathbf {Pr}[ \, o \, | \, a,b \, ] \cdot \mathbf {Pr}[ \, a,b \, ] \\&= \; \mathbf {Pr}[ \, o \, | \, a,b \, ] \cdot 1&\text{ since }\,\,b \,\,\mathrm{and}\,\,a\,\,\mathrm{are\,\, fixed} \\&= \; {\sum _{s \in S}} \mathbf {Pr}[ \, o \, | \, a,s \, ] \cdot b(s)&\text{ by } \text{ definition } \text{ of }\,\, \,b \\&= \; {\sum _{s \in S}} \left( \sum _{s' \in S} \mathbf {Pr}[ \, o \, | \, s',a \, ] \cdot P(s,a)(s') \right) \cdot b(s)&\text{ by } \text{ definition } \text{ of } \,\,\,P \\&= \; {\sum _{s \in S}} \left( \sum _{s' \in S \wedge obs (s')=o} P(s,a)(s') \right) \cdot b(s)&\text{ by } \text{ definition } \text{ of }\, obs . \end{aligned}$$

Combining these results (and rearranging) we have:

$$\begin{aligned} b^{a,o}(s') \; = \; \left\{ \begin{array}{ll} \frac{\sum _{s \in S} P(s,a)(s') \cdot b(s)}{\sum _{s \in S} b(s) \cdot \left( \sum _{s^{{\scriptstyle \prime \prime }} \in S \wedge obs (s^{{\scriptstyle \prime \prime }})=o} P(s,a)(s'') \right) } &{} \quad {\mathrm{if}\,\, obs (s')=o} \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

Now using this we can define the probabilistic transition function of the belief MDP ${\mathcal {B}}(\mathsf{M})$. Suppose we are in a belief state b and we perform action a. Now the probability we move to belief $b'$ is given by:

$$\begin{aligned} P^{\mathcal {B}}_T(b,a)(b') = \mathbf {Pr}[ \, b' \, | \, a,b \, ] \; = \; \sum _{o \in O} \mathbf {Pr}[ \, b' \, | \, o,a,b \, ] \cdot \mathbf {Pr}[ \, o \, | \, a,b \, ] . \end{aligned}$$

The first term in the summation ($\mathbf {Pr}[ \, b' \, | \, o,a,b \, ]$) is the probability of being in belief $b'$ after being in belief b, performing action a and observing o. Therefore by definition of $b^{a,o}$, this probability will equal 1 if $b'$ equals $b^{a,o}$ and 0 otherwise.

For the second term, as in the derivation of the denominator above, we have:

$$\begin{aligned} \mathbf {Pr}[ \, o \, | \, a,b \, ] = {\sum _{s \in S}} b(s) \cdot \left( \sum _{s' \in S \wedge obs (s')=o} P(s,a)(s') \right) \end{aligned}$$

This completes the construction of the transition function of the belief MDP.

It remains to construct the reward structure $R^{\mathcal {B}}$ of the belief MDP. In this case, we just have to take the expectation of the state and action reward functions with respect to the current belief, i.e. for any belief state b and action a:

$$\begin{aligned} R^{\mathcal {B}}_S(b)= & {} {\sum _{s \in S}} R_S(s) \cdot b(s) \\ R^{\mathcal {B}}_A(b,a)= & {} {\sum _{s \in S}} R_A(s,a) \cdot b(s) . \end{aligned}$$