Abstract
The general idea of guilt aversion is that agents may be motivated to avoid letting others down, even at the expense of their own material payoff. Several experimental studies have documented behavior that is consistent with agents exhibiting guilt averse motivations in social interactions. However, there are strategic implications of guilt aversion, which can impact economic outcomes in important ways, that have yet to be explored. I introduce a game that admits the possibility for agents to induce guilt upon others in a manner consistent with the method posited by Baumeister et al. (Psychol Bull 115:243–267, 1994). This game enables me to experimentally test whether agents attempt to exploit the guilt aversion of others by inducing guilt upon them, and whether agents are actually susceptible to this exploitation. Additionally, the design enables me to test whether agents exhibit higher degrees of trust when they are given such an opportunity to exploit the guilt aversion of others. The data suggest that agents do not attempt to fully exploit the guilt aversion of other agents by inducing guilt upon them; however, the data suggest that agents would have been susceptible to guilt induction.



Similar content being viewed by others
Notes
For a more thorough discussion of the psychological foundations of guilt, I refer interested readers to Hoffman (1982), Tangney (1990), Tangney and Fischer (1995), Baumeister et al. (1994, 1995), and Tangney and Dearing (2002). Formal game theoretic models of guilt aversion have been developed by Dufwenberg (2002), for a specific game, and later by Battigalli and Dufwenberg (2007) for a general class of games.
Other studies documenting guilt averse behavior include Nelissen et al. (2011) in an ultimatum game, and Dufwenberg et al. (2011) in a public goods game. Relatedly, Bellemare et al. (2011) document direct evidence of agents willing to pay (positive monetary amounts) to avoid letting others down. On the contrary, Ellingsen et al. (2010) Kawagoe and Narita (2014) find little experimental support for guilt aversion.
Sub-standard effort by employees is likely to result in lower profits for a firm. Assuming that bonuses are increasing in firm profits, then lower profits would lead to lower bonuses for all employees. Thus, shirking by one employee could adversely affect the well-being of other employees.
This example was inspired by an editor who revealed to me that some assistant professors do actually inform the editor, at the time of submission, about such an upcoming tenure review!
I note here that I am by no means implying that these two conditions are necessary for an agent to feel guilt, as is evident by prior studies that have effectively studied guilt in games that have no private information. Rather, my claim is that these two conditions are necessary for one agent to induce guilt upon another agent, i.e., for one agent to increase the amount of guilt another agent may feel from acting in an undesirable way.
A study by Fong et al. (2007) uses a trust game with private information. However, the authors incorporate private information as a means of testing their model of guilt driven reciprocity. Additionally, their trust game features private information for the second mover, while I will consider a trust game with private information for the first mover, as will be shown in the next section. Güth et al. (2014) consider a trust game with uncertain payoffs, but not private information, as a way of testing how payoff uncertainty impacts trust and reciprocity.
I use the term “guilt induction” when referring to this type of strategic attempt by Player A to exploit the guilt aversion of Player B and influence the behavior of Player B. I do this to remain consistent with the psychological foundations and terminology outlined by BSH (1994). However, in relation to the Battigalli and Dufwenberg (2007) model of guilt, it may be more pedagogical to think of this strategic behavior from Player A as “counterfactual” guilt induction. Essentially, Player A is trying to increase the amount of guilt that Player B would feel as a result of choosing an action that is undesirable for Player A. This makes the guilt counterfactual in the sense that Player B may never experience the guilt if he/she chooses an action that complies with Player A’s desired action.
B&D also model a second form of guilt, “guilt from blame.” However, in this paper I will consider only simple guilt and, therefore, for the remainder of the paper when I refer to the guilt model of B&D, I am implicitly referring to the model of simple guilt. The B&D model is an application of the authors’ more general theoretical framework developed in Battigalli and Dufwenberg (2009), which extends the psychological game theory framework pioneered by Geanakopolos et al. (1989).
Namely, a game where the first mover has an opportunity to choose an action that creates the possibility of mutual benefit if the other person cooperates, but a risk of lower payoffs to oneself if the other person defects. Such an action taken by the first mover is consistent with the behavioral definitions of trust presented in Cox (2004) and Fehr (2009).
In \(\Gamma _{\mathrm{PPT}},\) there is a multiplicity of Perfect Bayesian Equilibria for selfish players that depend on the specification of Player B’s beliefs at the information set where no information is conveyed regarding the value of X. However, regardless of Player B’s beliefs, it is rational for him/her to choose Left and subsequently, it is sequentially rational for Player A to choose Out. Therefore, the unique equilibrium outcome of \(\Gamma _{\mathrm{PPT}}\) is the game ending with Player A choosing Out.
The notation of \({\widehat{m}}_{A}\) is consistent with the notation used in the B&D model of guilt aversion and anticipates the upcoming application of the model to \(\Gamma _{\mathrm{PPT}}\).
Note, if all Player As (who chose In) were revealed the value of X (as opposed to only 80 % of them), then it would be possible, even probable, for Player B’s belief about the value of X when it is not conveyed to be \(X=6.\) Such a belief would be consistent with Player B thinking that only a Player A for whom \(X=6\) would choose Not Convey. Under this belief structure, the degree to which Player A suffers from Player B’s choice of Left, from Player B’s perspective, would be equal when \(X=6\) is conveyed and when X is not conveyed. Furthermore, if Player A anticipated beliefs of this sort from Player B, then Player A would be indifferent between conveying and not conveying \(X=6\); at least as far as attempted guilt induction is concerned. Hence, the inclusion of the move by Nature to reveal the value of X to Player A with \(\hbox {prob}=4/5\) ensures that Player As who want to attempt to induce guilt upon Player B are motivated to Not Convey \(X=6\) (according to the BSH 1194 method).
Note, if all Player As attempt to induce guilt, then \(X=6\) would never actually be conveyed to Player B; thus, no data would be generated on the proportion on Player Bs choosing Right after \(X=6\) was conveyed. In this case, H2 would just reduce down to the binary comparison of the proportion of Player Bs choosing Right after \(X=0\) was conveyed to when the value of X was not conveyed. However, as we will see in the Results section, some Player As do convey \(X=6,\) so the necessary data are generated to test H2 as it is stated.
To illustrate, consider the application of the Fehr and Schmidt (1999) model to Player B in \(\Gamma _{\mathrm{PPT}}\). An inequality averse Player B playing \(\Gamma _{\mathrm{PPT}}\) always prefers the payoff vector (X, 6) to the payoff vector (10, 4) \(\forall X\in [0,6].\) To see this, note that for the extreme case where \(X=0,\) we have that \(6-\beta (6-0)>4-\alpha (10-4)\) \(\forall \beta \in [0,1)\) and \(\alpha \ge \beta ,\) where the LHS represents an inequality averse Player B’s utility from choosing Left and the RHS represents the utility from choosing Right. For the other extreme case where \(X=6,\) we have that \(6>4-\alpha (10-4)\) \(\forall \alpha \ge 0,\) where the LHS represents an inequality averse Player B’s utility from choosing Left and the RHS represents the utility from choosing Right. The constraints that \(\beta \in [0,1)\) and \(\alpha \ge \beta \) in the above inequalities are assumed a priori in the FS model.
In my view it is even much less plausible that this could confound the inference regarding Player A’s attempted guilt induction of Player B (H1). Specifically, this argument would require Player A to somehow anticipate that Player B had inequality averse preferences based on relative payoffs shares (e.g., the Bolton and Ockenfels model), as well as then reason through that conveying \(X=0\) induces a payoff vector where such an inequality averse Player B would then be more motivated to choose Right. That being said, I do acknowledge that this is a possible confound and shortcoming of the experimental design.
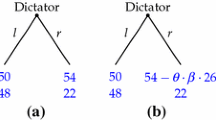
This approach of controlling for the possible reciprocity concerns of Player B in the trust game (\(\Gamma _{\mathrm{PPT}}\)) by using the corresponding dictator game (\(\Gamma _{\mathrm{PPD}}\)) was inspired by the triadic design approach developed and implemented in Cox (2004).
Alternatively, a simple probit regression, with Right as the dependent variable and the conveyance state as the independent variable (where \(X=6\) is coded as a zero, \(X=NC\) is coded as a one, and \(X=0\) is coded as a two) also yields a significantly positive coefficient \((p = 0.001)\) on the conveyance state variable.
Some factors that may have contributed to the higher levels of conveyance in the PPD treatment include, but are not limited to: (i) lack of the selection effect that could have been present in the PPT treatment, since all Player As were forced to make a conveyance decision in PPD, (ii) that inability to signal trust in PPD, which may have prompted Player As to be more likely to attempt to signal honesty by conveying X in hopes of increasing the likelihood of Player B choosing the kind allocation, and/or (iii) activity bias/experimenter demand effects for Player As in the PPD treatment.
The 38 and 52 % observed rates of trust are largely consistent with findings in prior studies that have implemented variations of binary choice trust games. For example, Bohnet and Huck (2004) document a range of trust rates from 19–59 %, Charness and Dufwenberg (2006) from 23–74 %, Charness and Dufwenberg (2011) from 44–80 %, and Charness et al. (2011) from 25–54 %.
I thank two anonymous reviewers for aptly calling attention to these possible alternative explanations.
I note, however, that agents may be motivated by non-material incentives to align their ex post beliefs about guilt perceptions with their behavior. An example of such a motivation would be to avoid the disutility or discomfort associated with the inconsistency between beliefs and actions, a phenomenon that psychologists generally refer to as cognitive dissonance. Hence, the maintained disclaimer about interpreting these questionnaire results with caution.
Because of the way the questionnaire was programmed in z-tree and administered, it was possible for subjects to fail to submit an answer for each question. A total of 5 of 98 Player As who had the value of X revealed to them failed to answer at least one of the questions related to their beliefs of Player B’s guilt feelings. Therefore, the aggregate data in Table 4 reflect the responses of 93 Player As who did answer both questions.
One seemingly inconsistent pattern that emerges from Table 4 is the comparison of the average level of reported guilt that Player A thought Player B would feel from choosing Left when “Player B did not know X” (column 2), depending on whether Player As were revealed \(X=0\) (Panel 1) or \(X=6\) (Panel 2). In the former case, the average reported level of guilt is approximately 1.85 (aggregated over Player As who did and did not convey X), which is significantly lower than in the latter case, where the average reported level of guilt is approximately 2.35. I speculate that this difference is the result of an anchor/adjustment process. Specifically, Player As for whom \(X=0\) report a high level of guilt that Player B would feel from choosing Left if \(X=0\) was known (the anchor point), and then adjust this level downward if X was unknown. Those Player As for whom \(X=6\) report a low level of guilt that Player B would feel from choosing Left if \(X=6\) was known (the anchor point), and then adjust this level upward if X was unknown. Thus, the difference is post-adjusted levels of reported guilt is likely a result of the initial anchoring level and the corresponding magnitude of the adjustment. That said, the analysis of the questionnaire data was done using a sign rank test of matched data for each participant, and the identified effects are based on the relative differences in the participants’ reported level of guilt across the two questions. As a result, possible anchoring effects that may distort the absolute level of reported guilt, do not invalidate the matched pairs analysis based on the relative comparison of guilt across questions.
A total of 7 of 124 of the Player Bs did not answer at least one of the questions related to their guilt feelings. Therefore, the aggregate data in Table 5 reflect the responses of 117 Player Bs who did answer both questions.
Specifically, Dufwenberg and Gneezy (2000), Charness and Dufwenberg (2006), Bacharach et al. (2007), and Dufwenberg et al. (2011) elicited second-order beliefs and test for a positive correlation between elicited second-order expectations and actions. However, because these studies provide only a correlation between elicited second-order beliefs and actions, anchoring and false consensus effects cannot be ruled out as possible explanations. Alternatively, Reuben et al. (2009) and Ellingsen et al. (2010) elicit first-order expectations of subjects, convey those expectations to the subject’s partner, and test for correlations between expectations and actions. However, the possibility of untruthful reporting of beliefs and skepticism of conveyed beliefs arise with this approach, as noted by Reuben et al.
Evidence of such opportunistic behavior by experts in credence goods has been found in a recent field experiment by Balafoutas et al. (2013). In particular, the authors find evidence of systematic over-charging and over-treating of passengers by taxi drivers in Greece.
That is, building a trustworthy reputation through prior trustworthy actions, that are observable to other agents, induces agents to trust you in the future. Many experimental studies have found evidence consistent with this “indirect reciprocity” including Bohnet and Huck (2004), Bolton et al. (2005), Greiner and Levati (2005), Seinen and Schram (2006), Duffy et al. (2008), Engelmann and Fischbacher (2009), and Huck et al. (2012). Charness et al. (2011) provide a thorough review of much of this literature as well as provide experimental evidence that a reputation of trusting behavior can foster trust.
B&D model two types of guilt for a general class of extensive form games, simple guilt and guilt from blame. With simple guilt, an agent suffers disutility proportional to how much he/she lets down another agent. However, with guilt from blame, an agent suffers disutility proportional to how much the other agent blames him/her for being let down. Thus, the main difference between the two models is the extent to which an agent can be blamed for letting down another agent. With respect to \(\Gamma _{\mathrm{PPT}},\) the two models are equivalent. Player A can unambiguously identify the action of Player B, which implies that Player B will receive all the blame for letting Player A down. Although either of these models of guilt could be used for this analysis, I opt to apply the less complex model of simple guilt for clarity.
I refer the reader to the authors’ more general paper, Battigalli and Dufwenberg (2009), for a formal equilibrium analysis of dynamic psychological games. The authors extend the concept of sequential equilibrium by incorporating hierarchies of conditional beliefs.
This assumption that Player A (the trustor) does not experience guilt is consistent with the model of “role-dependent guilt” developed by Attanasi et al. (2015). Because participants are randomly drawn from the same population to play the role of Player A or Player B, this assumption is consistent with the idea that the guilt sensitivity of a participant becomes an actual tendency when they are assigned the role of Player B, as asserted by Attanasi et al. (2015). This assumption that the trustor is not affected by guilt, which is common knowledge, is also employed by Attanasi et al. (2013).
I thank an anonymous reviewer for calling my attention to this paper, as well as making several apt suggestions of how to incorporate its main insights into the theoretical guilt aversion analysis of \(\Gamma _{\mathrm{PPT}}\).
I refer interested readers to Attanasi et al. (2015) for the formal development of the incomplete information model of guilt aversion and the corresponding exhaustive equilibrium analysis.
The condition that Player Bs need to have sufficiently low \(\theta _{B}\)s to ensure the “selfish” equilibrium outcome is a result of the fact that \(\Gamma _{\mathrm{PPT}}\) has a chance move. If there were no chance moves, then we would have existence of the selfish equilibrium for all types of Player As and Player Bs (see, specifically, Remark 1 in Attanasi et al. 2015 and Observation 2 from B&D more generally). However, because of the chance move in \(\Gamma _{\mathrm{PPT}}\) it is possible for Player A to still be let down from B’s choice of Left (if chance were to chose \(X=0\)), even if Player B believes that Player A expected him/her to choose Left. For the specific parameterization of \(\Gamma _{\mathrm{PPT}}\), assuming all Player Bs have \(\theta _{B}\le \frac{2}{3}\) would be sufficient for the existence of the selfish equilibrium for all types.
References
Attanasi, G., Battigalli, P., & Manzoni, E. (2015). Incomplete information models of guilt aversion in the trust game. Management Science, forthcoming.
Attanasi, G., Battigalli, P., & Nagel, R. (2013). Disclosure of belief-dependent preferences in a trust game. IGIER Working Paper No. 506, Bocconi University.
Bacharach, M., Guerra, G., & Zizzo, D. (2007). The self-fulfilling property of trust: An experimental study. Theory and Decision, 63, 349–388.
Balafoutas, L., Beck, A., Kerschbamer, R., & Sutter, M. (2013). What drives taxi drivers? A field experiment on fraud in a market for credence goods. Review of Economic Studies, 80, 876–891.
Battigalli, P., & Dufwenberg, M. (2007). Guilt in games. American Economic Review, 97, 170–176.
Battigalli, P., & Dufwenberg, M. (2009). Dynamic psychological games. Journal of Economic Theory, 144, 1–35.
Baumeister, R., Stillwell, A., & Heatherton, T. (1994). Guilt: An interpersonal approach. Psychological Bulletin, 115, 243–267.
Baumeister, R., Stillwell, A., & Heatherton, T. (1995). Personal narratives about guilt: Role in action control and interpersonal relationships. Basic and Applied Social Psychology, 17, 173–198.
Beck, A., Kerschbamer, R., Qiu, J., & Sutter, M. (2013). Shaping beliefs in experimental markets for expert services: Guilt aversion and the impact of promises and money-burning options. Games and Economic Behavior, 81, 145–164.
Bellemare, C., Sebald, A., & Strobel, M. (2011). Measuring the willingness to pay to avoid guilt: Estimation using equilibrium and stated belief models. Journal of Applied Econometrics, 26, 437–453.
Bellemare, C., Kröger, S., & Van Soest, A. (2008). Measuring inequity aversion in a heterogeneous population using experimental decisions and subjective probabilities. Econometrica, 76, 815–839.
Berg, J., Dickhaut, J., & McCabe, K. (1995). Trust, reciprocity and social history. Games and Economic Behavior, 10, 122–142.
Bohnet, I., & Huck, S. (2004). Repetition and reputation: Implications for trust and trustworthiness when institutions change. American Economic Review Papers and Proceedings, 94, 362–366.
Bolton, G., Katok, E., & Ockenfels, A. (2005). Cooperation among strangers with limited information about reputation. Journal of Public Economics, 89, 1457–1468.
Bolton, G., & Ockenfels, A. (2000). A theory of equity, reciprocity, and competition. American Economic Review, 90, 166–193.
Brandts, J., & Charness, G. (2003). Truth or consequences: An experiment. Management Science, 49, 116–130.
Charness, G., Du, N., & Yang, C. (2011). Trust and trustworthiness reputations in an investment game. Games and Economic Behavior, 72, 361–375.
Charness, G., & Dufwenberg, M. (2006). Promises and partnership. Econometrica, 74, 1579–1601.
Charness, G., & Dufwenberg, M. (2010). Bare promises: An experiment. Economics Letters, 107, 281–283.
Charness, G., & Dufwenberg, M. (2011). Participation. American Economic Review, 101, 1211–1237.
Charness, G., & Rabin, M. (2002). Understanding social preferences with simple tests. Quarterly Journal of Economics, 117, 817–869.
Cox, J. (2004). How to identify trust and reciprocity. Games and Economic Behavior, 46, 260–281.
De Hooge, I. E., Nelissen, R., Breugelmans, S. M., & Zeelenberg, M. (2011). What is moral about guilt? Acting “prosocially” at the disadvantage of others. Journal of Personality and Social Psychology, 100, 462.
Duffy, J., Lee, Y., & Xie, H. (2008). Social norms, information, and trust among strangers: An experimental study. Columbia: Mimeo.
Dufwenberg, M. (2002). Marital investments, time consistency, and emotions. Journal of Economic Behavior and Organization, 48, 57–69.
Dufwenberg, M., Gächter, S., & Hennig-Schmidt, H. (2011). The framing of games and the psychology of play. Games and Economic Behavior, 73, 459–478.
Dufwenberg, M., & Gneezy, U. (2000). Measuring beliefs in an experimental lost wallet game. Games and Economic Behavior, 30, 163–182.
Dufwenberg, M., & Kirchsteiger, G. (2004). A theory of sequential reciprocity. Games and Economic Behavior, 47, 268–298.
Dufwenberg, M., Smith, A., & Van Essen, M. (2013). Hold-up: With a vengeance. Economic Inquiry, 51, 896–908.
Dulleck, U., & Kerschbamer, R. (2006). On doctors, mechanics, and computer specialists: The economics of credence goods. Journal of Economic Literature, 44, 5–42.
Dulleck, U., Kerschbamer, R., & Sutter, M. (2011). The economics of credence goods: On the role of liability, verifiability, reputation and competition. American Economic Review, 101, 526–555.
Ellingsen, T., Johannesson, M., Tjotta, S., & Torsvik, G. (2010). Testing guilt aversion. Games and Economic Behavior, 68, 95–107.
Engelmann, D., & Fischbacher, U. (2009). Indirect reciprocity and strategic reputation building in an experimental helping game. Games and Economic Behavior, 67, 399–407.
Engelmann, D., & Strobel, M. (2004). Inequality aversion, efficiency, and maximin preferences in simple distribution experiments. American Economic Review, 94, 857–869.
Erat, S., & Gneezy, U. (2012). White lies. Management Science, 58, 723–733.
Fehr, E. (2009). On the economics and biology of trust. Journal of the European Economic Association, 7, 235–266.
Fehr, E., & Schmidt, K. (1999). A theory of fairness, competition, and cooperation. Quarterly Journal of Economics, 114, 817–868.
Fischbacher, U. (2007). z-Tree, toolbox for readymade economic experiments. Experimental Economics, 10, 171–178.
Fong, Y., Huang, C., & Offerman, T. (2007). Guilt driven reciprocity in a psychological signaling game. Working Paper.
Geanakopolos, J., Pearce, D., & Stacchetti, E. (1989). Psychological games and sequential rationality. Games and Economic Behavior, 1, 60–79.
Gneezy, U. (2005). Deception: The role of consequences. American Economic Review, 95, 384–394.
Gneezy, U., & Imas, A. (2014). Materazzi effect and the strategic use of anger in competitive interactions. Proceedings of the National Academy of Sciences, 111(4), 1334–1337.
Greiner, B., & Levati, V. (2005). Indirect reciprocity in cyclical networks: An experimental study. Journal of Economic Psychology, 26, 711–731.
Güth, W., Mugera, H., Musau, A., & Ploner, M. (2014). Deterministic versus probabilistic consequences of trust and trustworthiness: An experimental investigation. Journal of Economic Psychology, 42, 28–40.
Hoffman, M. L. (1982). Development of prosocial motivation: Empathy and guilt. In N. Eisenberg (Ed.), The development of prosocial behavior (pp. 281–313). New York: Academic Press.
Huck, S., Lünser, G., & Tyran, J.-R. (2012). Competition fosters trust. Games and Economic Behavior, 76, 195–209.
Kawagoe, T., & Narita, Y. (2014). Guilt aversion revisited: An experimental test of a new model. Journal of Economic Behavior & Organization, 102, 1–9.
Lee, S. Y. (2010). Economics of Guanxi as an interpersonal investment game. Review of Development Economics, 14, 333–342.
Nelissen, R., Leliveld, M. C., van Dijk, E., & Zeelenberg, M. (2011). Fear and guilt in proposers: Using emotions to explain offers in ultimatum bargaining. European Journal of Social Psychology, 41, 78–85.
Rabin, M. (1993). Incorporating fairness into game theory and economics. American Economic Review, 83, 1281–1302.
Reuben, E., Sapienza, P., & Zingales, L. (2009). Is mistrust self-fulfilling? Economic Letters, 104, 89–91.
Sapienza, P., & Toldra, A. & Zingales, L. (2013). Understanding trust. The Economic Journal, 123, 1313–1332.
Seinen, I., & Schram, A. (2006). Social status and group norms: Indirect reciprocity in a helping experiment. European Economic Review, 50, 581–602.
Tangney, J. (1990). Assessing individual differences in proneness to shame and guilt: Development of the self-conscious affect and attribution inventory. Journal of Personality and Social Psychology, 59, 102–111.
Tangney, J., & Dearing, R. (2002). Shame and guilt. New York: Guilford Press.
Tangney, J., & Fischer, K. (1995). Self-conscious emotions: Shame, guilt, embarrassment, and pride. New York: Guilford Press.
Vangelisti, A., Daly, J., & Rudnick, J. (1991). Making people feel guilty in conversations: Techniques and correlates. Human Communication Research, 18, 3–39.
Wang, C. S., Galinsky, A. D., & Murnighan, J. K. (2009). Bad drives psychological reactions, but good propels behavior responses to honesty and deception. Psychological Science, 20, 634–644.
Wang, C. S., & Leung, A. K. Y. (2010). The cultural dynamics of rewarding honesty and punishing deception. Personality and Social Psychology Bulletin, 36, 1529–1542.
Acknowledgments
E. Cardella would like to thank the editor and three anonymous reviewers for helpful comments. E. Cardella also thanks Pierpaolo Battigalli, Anna Breman, Gary Charness, Martin Dufwenberg, Price Fishback, Paul Heidhues, Tamar Kugler, Alec Smith, John Wooders, participants at the ESA conference in Tucson, participants from BABEEW at Santa Clara University, and seminar participants at the University of Arizona, Rochester Institute of Technology, University of Mississippi and Bowdoin College for valuable discussion and additional helpful comments. This project was funded by the Economic Science Laboratory (ESL) and the National Science Foundation (NSF) (Grant # SES-0819780).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Application of B&D model of guilt
In this Appendix, I formalize the arguments put forth in Sect. 2.3 regarding the connection between the posited method by BSH (1994) of how guilt is induced and the formal model of guilt developed by B&D. In doing so, I first provide a brief outline of the B&D model of guilt, followed by its application to \(\Gamma _{\mathrm{PPT}}\). I then derive conditions under which the BSH (1994) method is consistent with predictions of the B&D model of guilt. I conclude by showing that the BSH (1994) method can be supported as an equilibrium in \(\Gamma _{\mathrm{PPT}}\) under the framework of the B&D model. I conclude by briefly discussing the recent extension of the B&D model developed by Attanasi et al. (2015) that incorporates incomplete information about guilt sensitivities, and how incomplete information about guilt sensitivities can impact behavioral predictions in \(\Gamma _{\mathrm{PPT}}\).
1.1 B&D model of guilt applied to \(\Gamma _{\mathrm{PPT}}\)
Before I proceed in formally applying the B&D model of guilt to \(\Gamma _{\mathrm{PPT}},\) I first provide a general overview of the B&D model of simple guilt.Footnote 30 What follows is only a simplified outline of the model. Interested readers should refer to B&D for the full, technical presentation of the model including illustrative examples. Informally, the model posits that agents suffer disutility, in the form of guilt, from failing to live up to others’ expectations. This is captured by modeling an agent’s utility as a function of his/her own material payoffs and the extent to which he/she let other agents down.
Formally, simple guilt is modeled by specifying a utility function for player i given by:
In this expression, \(m_{i}\) represents player i’s material payoff, and \(\underset{j\ne i}{\sum }\theta _{ij}\cdot D_{j}\) represents player i’s disutility from simple guilt. The latter component is composed of two pieces. The first, \(\theta _{ij}\), is an exogenously given constant that measures player i’s sensitivity of feeling guilty toward player j. The second, \(D_{j}\), represents the amount by which player i lets player j down, as a result of player i’s strategy. \(D_{j}=E_{j}-m_{j}\) is expressed as the difference between the material payoff that player j was expecting, \(E_{j}\), and the material payoff that player j actually receives, \(m_{j}.\) \(E_{j}\) itself is a function of player j’s strategy, and player j’s vector of “first-order” beliefs regarding the strategies of the other players. Note, player i does not actually observe \(D_{j}\), as it is a function of player j’s first-order beliefs. Therefore, it is assumed that player i maximizes the expected value of \( u_{i}^{\mathrm{SG}}\), given player i’s first-order beliefs regarding player j’s strategy, and player i’s “second-order” belief regarding player i’s first-order beliefs.
In proceeding with the application of the B&D model of simple guilt to \( \Gamma _{\mathrm{PPT}}\), I derive the guilt that Player B would experience from choosing Left in \(\Gamma _{\mathrm{PPT}}\) at each of the three possible conveyance states (histories): (i) \(X=0\) was conveyed, which I denote \(C^{0}\), (ii) \(X=6\) was conveyed, which I denote \(C^{6}\), and (iii) the value of X was not conveyed, which I denote \(C^{N}\). A strategy for Player B is a probability distribution over Player B’s possible actions, {Left, Right}, at each of the three possible conveyance states. In deriving this guilt that Player B would suffer from choosing Left, it is necessary to first derive Player A’s material expectation. Before Player A makes her initial In or Out decision, Player A forms an initial first-order belief regarding Player B’s strategy, which can be represented as the probabilities that Player B would choose Right at each of the three conveyance states; I denote this vector of probabilities as \({\varvec{\alpha }}_{A}=(\Pr ({ Right }|C^{0}),\Pr ({ Right }|C^{N}),\Pr ({ Right }|C^{6})).\) For a given strategy, Player A forms an initial expectation, which I denote \(E_{A},\) weighted over \({\varvec{\alpha }}_{A}\) and moves by Nature, of her material payoff.
Player B experiences disutility from simple guilt when he chooses a strategy that yields a payoff to Player A that is lower than \(E_{A}\). However, Player B does not observe \(E_{A}.\) Therefore, Player B must form an expectation of \(E_{A},\) conditional on the conveyance state. I define this conditional expectation of \(E_{A}\) as \(E_{B}|h\) where \(h\in \{C^{0},C^{N},C^{6}\}\), which is implicitly a function of Player B’s conditional second-order beliefs regarding \({\varvec{\alpha }}_{A}\). The guilt that Player B would suffer from choosing Left is proportional to the difference between \(E_{B}|h\) and \(m_{A},\) where \(m_{A}\) is the material payoff that Player A actually receives as a result of Player B’s Left decision. Let \(\theta _{B}\ge 0\) denote Player B’s sensitivity to feeling guilty. Below is the amount of simple guilt that Player B would suffer from choosing Left at each of the three possible conveyance states.
-
\(X=0\) was conveyed: Because the conveyance is credible, Player B knows that if he chooses Left, Player A will receive a payoff of \(m_{A}=0\). Player B’s expectation of Player A’s expectation is \(E_{B}|C^{0}.\) By choosing Left, Player B will suffer disutility from guilt equal to \(\theta _{B}\cdot (E_{B}|C^{0}-0).\) Thus, Player B’s utility from choosing Left, after \(X=0\) was conveyed, is equal to:
$$\begin{aligned} 6-\theta _{B}\cdot (E_{B}|C^{0}-0) \end{aligned}$$ -
\(X=6\) was conveyed: Because the conveyance is credible, Player B knows that if he chooses Left, Player A will receive a payoff of \(m_{A}=6\). Player B’s expectation of Player A’s expectation is \(E_{B}|C^{6}.\) By choosing Left, Player B will suffer disutility from guilt equal to \(\theta _{B}\cdot (E_{B}|C^{6}-6).\) Thus, Player B’s utility from choosing Left, after \(X=0\) was conveyed, is equal to:
$$\begin{aligned} 6-\theta _{B}\cdot (E_{B}|C^{6}-6) \end{aligned}$$ -
Value of X not conveyed: If the value of X is not conveyed, then Player B must think about the expected material payoff that Player A would receive if he chooses Left. Let \({\widehat{m}}_{A}=E_{B}[m_{A}|C^{N}]\) denote this expectation. As I have previously shown (see Sect. 2.1), \({\widehat{m}}_{A}\in [1,5]\). Player B’s expectation of Player A’s expectation is \(E_{B}|C^{N}.\) By choosing Left, Player B will suffer disutility from guilt equal to: \(\theta \cdot (E_{B}|C^{N}-{\widehat{m}}_{A})\) where \({\widehat{m}}_{A}\in [1,5].\) Thus, Player B’s utility from choosing Left, after the value of X was not conveyed, is equal to:
$$\begin{aligned} 6-\theta _{B}\cdot (E_{B}|C^{N}-{\widehat{m}}_{A})\quad \hbox {where } {\widehat{m}}_{A}\in [1,5] \end{aligned}$$
1.2 Guilt induction in \(\Gamma _{\mathrm{PPT}}\) via the B&D model of guilt
Based on the BSH (1994) method for how an agent can induce guilt upon another, it was derived that Player A could attempt to induce guilt upon Player B in \(\Gamma _{\mathrm{PPT}}\) by choosing to Convey \(X=0\) and Not Convey \(X=6\). In what follows, I derive conditions under which this is consistent with predictions of the B&D model of simple guilt. From the previous section, we derived that the disutilities, from feeling guilt, that Player B would suffer from choosing Left at each of the three possible conveyance states are:
-
\(X=0\) was conveyed: \(\theta _{B}\cdot (E_{B}|C^{0}-0)\)
-
\(X=6\) was conveyed: \(\theta _{B}\cdot (E_{B}|C^{6}-6)\)
-
Value of X not conveyed: \(\theta _{B}\cdot (E_{B}|C^{N}-{\widehat{m}}_{A})\) where \({\widehat{m}}_{A}\in [1,5]\)
According to B&D, Player B would suffer more disutility from choosing Left when \(X=0\) was conveyed, compared to when the value of X was not conveyed, when:
Similarly, Player B would suffer more disutility from choosing Left when the value of X was not conveyed, compared to when \(X=6\) was conveyed, when:
Essentially, Condition 1 states that Player B’s second-order belief of Player A’s expectation after \(X=0\) is conveyed, \(E_{B}|C^{0},\) is not too much lower than Player B’s second-order belief of Player A’s expectation after the value of X is not conveyed, \(E_{B}|C^{N}.\) Similarly, Condition 2 states that Player B’s second-order belief of Player A’s expectation after the value of X is not conveyed, \(E_{B}|C^{N},\) is not too much lower than Player B’s second-order belief of Player A’s expectation after \(X=6\) is conveyed, \(E_{B}|C^{6}.\) Conditions 1 and 2 would certainly be satisfied if we assumed that Player B does not update his belief of Player A’s expectation (i.e., \(E_{B}|C^{0}=E_{B}|C^{N}=E_{B}|C^{6}\)), which would be satisfied in an equilibrium. However, making the assumption that \(E_{B}|C^{0}=E_{B}|C^{N}=E_{B}|C^{6}\) is clearly stronger than is needed for Condition 1 and 2 to be satisfied.
If Conditions 1 and 2 are satisfied, then the B&D model predicts that Player B would feel more guilt from choosing left after \(X=0\) was conveyed and the value of X was not conveyed, compared to when the value of X was not conveyed and \(X=6\) was conveyed, respectively. Therefore, if Condition 1 and 2 hold, then according to the B&D model, Player A can induce guilt upon Player B by choosing to Convey \(X=0\) and Not Convey \(X=6\), which is consistent with the BSH (1994) method for inducing guilt.
1.3 Guilt induction as an equilibrium of \(\Gamma _{\mathrm{PPT}}\)
Next, I show that effective guilt induction in \(\Gamma _{\mathrm{PPT}}\) can be supported as sequential equilibrium (SE) of \(\Gamma _{\mathrm{PPT}}\) under the framework of B&D.Footnote 31 The intuition behind this rests in the fact that in an SE, an assessment (profile of behavioral strategies and conditional hierarchical beliefs) will be consistent. Battigalli and Dufwenberg (2009) show that in equilibrium, “players never change their beliefs about the conditional beliefs that the opponents would hold at each h (history)” (pp. 16). Thus, in equilibrium, there is no belief updating. It follows that \(E_{B}|C^{0}=E_{B}|C^{N}=E_{B}|C^{6}\), which implies that Conditions 1 and 2 from above would be satisfied in an equilibrium. In this equilibrium analysis, I will assume that there is complete information regarding Player B’s guilt sensitivity, \(\theta _{B}\). While this assumption may be unrealistic, and not a feature of the design, it is common in the extant literature related to belief-dependent motivations (e.g., Charness and Dufwenberg 2006, 2011; Dufwenberg et al. 2013); furthermore, it allows me to focus on the motivation of this analysis, which is to establish that guilt induction can be supported as an equilibrium, without the information complexities that would otherwise need to be addressed. I also assume that Player A is not guilt averse, i.e., Player A’s guilt sensitivity is zero.Footnote 32
Guilt induction by Player A in \(\Gamma _{\mathrm{PPT}}\) is characterized by the choice to Convey \(X=0\) and Not Covey \(X=6\). Therefore, the strategy (In, Convey \(X=0\), Not Convey \(X=6\)) for Player A is consistent with attempted guilt induction. Effective guilt induction is characterized by Player B choosing Right as a response to the guilt induction by Player A. The following two strategies for Player B are consistent with responding in kind to Player A’s guilt induction: (Right \(\vert C^{0}\), Right \(\vert C^{N}\), Left \(\vert C^{6}\)), and (Right \(\vert C^{0}\), Left \(\vert C^{N}\), Left \(\vert C^{6}\)). Thus, the strategy profiles ((In, Convey \(X=0\), Not Convey \(X=6\)), (Right \(\vert C^{0}\), Right \(\vert C^{N}\), Left \(\vert C^{6}\))), and ((In, Convey \(X=0\), Not Convey \(X=6\)), (Right \(\vert C^{0}\), Left \(\vert C^{N}\), Left \(\vert C^{6}\))) are the candidate equilibrium profiles for effective guilt induction in \(\Gamma _{\mathrm{PPT}}\). In Claims 1 and 2 below, I show that each of these strategy profiles can be supported as an equilibrium of \(\Gamma _{\mathrm{PPT}}\).
Claim 1
The strategy profile ((In, Convey \(X=0\), Not Convey \(X=6\)), (Right \(\vert C^{0}\), Right \(\vert C^{N}\), Left \(\vert C^{6}\))) can be supported as a SE of \(\Gamma _{\mathrm{PPT}}\) for \(\theta _{B}\in [\frac{2}{5}, \frac{1}{2}]\).
To verify that this strategy profile is an equilibrium, we need to check that neither player has a profitable deviation. For Player A, this is rather trivial. By following the equilibrium strategy, Player A earns a payoff of 10, which is the highest payoff of the game. Therefore, Player A has no profitable deviation. For Player B, we need to consider deviations at each of the possible conveyance states. Given consistent beliefs in equilibrium, we have that \({\varvec{\alpha }}_{A}={\varvec{\beta }}_{B}=(1,1,0), E_{A}=E_{B}|h=10\ \forall h\in \{C^{0},C^{N},C^{6}\},\) and \({\widehat{m}}_{A}=5.\) Player B will not deviate to Right \(\vert C^{6}\) so long as: \(6-\theta _{B}\cdot [10-6]\ge 4\Leftrightarrow \theta _{B}\le \frac{1}{2}.\) Player B will not deviate to Left \(\vert C^{N}\) so long as: \(4\ge 6-\theta _{B}\cdot [10-5]\Leftrightarrow \theta _{B}\ge \frac{2}{5}.\) Similarly, Player B will not deviate to Left \(\vert C^{0}\) so long as: \( 4\ge 6-\theta _{B}\cdot [10-0]\Leftrightarrow \theta _{B}\ge \frac{1}{5}\) which is satisfied if \(\theta _{B}\ge \frac{2}{5}\).
Claim 2
The strategy profile ((In, Convey \(X=0\), Not Convey \(X=6\)), (Right \(\vert C^{0}\), Left \(\vert C^{N}\), Left \(\vert C^{6}\))) can be supported as a SE of \(\Gamma _{\mathrm{PPT}}\) for \(\theta _{B}\in [\frac{2}{7} ,1]\).
Again, to verify that this strategy profile is an equilibrium, we need to check that neither player has a profitable deviation. For Player A, playing the equilibrium strategy yields an expected payoff of 7; therefore, Player A cannot profitably deviate to Out. Player A would not deviate and Not Convey \(X=0\), which would result in a payoff of 0 compared to a payoff of 10 from following the equilibrium strategy to Convey \(X=0\). Player A is indifferent between Convey \(X=6\) and Not Convey \(X=6.\) Therefore, Player A has no profitable deviation from the prescribed equilibrium strategy. For Player B, we need to consider deviations at each of the possible conveyance states. Given consistent beliefs in equilibrium, we have that \({\varvec{\alpha }}_{A}={\varvec{\beta }}_{B}=(1,0,0), E_{A}=E_{B}|h=7\ \forall h\in \{C^{0},C^{N},C^{6}\},\) and \({\widehat{m}}_{A}=5.\) Player B will not deviate to Right \(\vert C^{6}\) so long as: \(6-\theta _{B}\cdot [7-6]\ge 4\Leftrightarrow \theta _{B}\le 2\). Player B will not deviate to Right \(\vert C^{N}\) so long as: \(6-\theta _{B}\cdot [7-5]\ge 4\Leftrightarrow \theta _{B}\le 1.\) Similarly, Player B will not deviate to Left \(\vert C^{0}\) so long as: \(4\ge 6-\theta _{B}\cdot [7-0]\Leftrightarrow \theta _{B}\ge \frac{2}{7}\).
1.4 Incomplete information regarding sensitivity to guilt
As I stated in the previous section, equilibrium Claims 1 and 2 assume common knowledge of Player B’s sensitivity to guilt, \(\theta _{B}.\) In a recent paper, Attanasi et al. (2015) have extended the B&D model to allow for incomplete information regarding guilt sensitivities in a 2-player trust game.Footnote 33 A formal application of their model to \(\Gamma _{\mathrm{PPT}}\) would require extensive theoretical preliminaries regarding the formulation of hierarchies of beliefs for each player via “type” structures, which is beyond the scope of this paper and would not add a proportionate increase in the main conclusions drawn. In addition, because I do not elicit any information about beliefs or types in the experiment (as the sessions were run prior the Attanasi et al. 2015 paper), I would be unable to derive precise predictions of the incomplete information model. As a result, I forgo a formal equilibrium analysis of \(\Gamma _{\mathrm{PPT}}\) under incomplete information; rather, I appeal to insights from the Attanasi et al. (2015) paper to provide some general discussion regarding how incomplete information about types could impact behavior in \(\Gamma _{\mathrm{PPT}}.\) Footnote 34
The main difference between the complete information and incomplete information extension of the guilt aversion model (as is most relevant to the discussion that follows) is that in an incomplete information setting where Player As and Player Bs are matched at random (as in the current experimental procedure), it is likely that participants hold heterogeneous and dispersed beliefs (Attanasi et al. 2013, p. 18). The important behavioral implication is that under complete information, there is likely to be much more polarization of behavior because the common knowledge of \(\theta _{B}\) enables coordination. Specifically, if \(\theta _{B}\) is small enough then Player B will not be susceptible to guilt induction and will choose Left, and Player A will choose Out (the standard payoff maximizing equilibrium outcome); on the other hand, if \(\theta _{B}\) is sufficiently large then Player B will be susceptible to guilt induction by Player A, and Player A could increase his/her payoff by choosing In and then inducing guilt (consistent with Claims 1 and 2 above).
However, with incomplete information about \(\theta _{B}\) (a reasonable assumption with regard to Player As in the experiment) more dispersion in beliefs and mis-coordination can arise, which can possibly lead to interesting patterns of behavior in \(\Gamma _{\mathrm{PPT}}\). Namely, many Player As could have held beliefs that Player Bs were not sensitive to guilt (i.e., low \(\theta _{B}\)), which may have motivated them to choose Out, which could explain why there was only a marginal 14 % increase in In rates between \(\Gamma _{\mathrm{PPT}}\) and \(\Gamma _{\mathrm{UPT}}.\) Additionally, for those Player As that did choose In (for other possible reasons besides attempting to exploit the guilt aversion of Player B), they would not be motivated to convey \(X=0\) and/or not convey \(X=6\) as a means of inducing guilt, as it would not be effective given their beliefs about \(\theta _{B}\) (which is consistent with the analysis of the questionnaire data in Table 4); these Player As may opt, for example, to Convey \(X=6\) to display honesty to Player B, consistent with the discussion in Sect. 4.3. On the other extreme, some Player As could have believed that Player Bs were very sensitive to feeling guilt (i.e., high \(\theta _{B}\)), such that Player B would be motivated to choose Right regardless of the conveyance state; in this case, these Player As would, again, not necessarily be motivated to convey \(X=0\) and/or not convey \(X=6\) as a means of inducing guilt, as it would not be necessary to motivate Player B to choose Right.
If we assume that Player As have incomplete information about Player B’s guilt sensitivity, \(\theta _{B},\) then multiple equilibria can arise in \(\Gamma _{\mathrm{PPT}}\), as in the case with perfect information. In particular, the “selfish” equilibrium exists that results in Player A always choosing Out since Player B would always choose Left, if Player Bs have sufficiently low \(\theta _{B}\)s.Footnote 35 In addition, by placing some restrictions on the distribution of \(\theta _{B}\) (e.g., assuming \(\theta _{B}\in [\frac{2}{7},1]\)), equilibria that correspond to effective guilt induction (those specified in Claims 1 and 2 above) can also arise. However, with incomplete information regarding \(\theta _{B}\), players do not have the ability to coordinate based on \(\theta _{B}\); hence, it is much more likely to observe heterogeneity in behavior because of the dispersion in beliefs (as shown by Attanasi et al. 2013). As a result, the fact that participants playing the role of Player A posses incomplete information regarding Player B’s sensitivity to guilt could explain some of the observed patterns in the data; namely, why only marginally more Player As chose In in \(\Gamma _{\mathrm{PPT}}\), as well as the conveyance behavior inconsistent with attempted guilt induction, where Player As choose to Not Convey \(X=0\) and Convey \(X=6\).
Appendix B.1: Copy of experimental instructions
1.1 Sample instructions: PPT treatment
Welcome and thank you for participating. Your participation is VOLUNTARY, and you may leave at any time. Feel free to raise your hand and ask questions at any time, and you may refer back to these instructions at any time during the session. Please remain seated and quiet for the remainder of the session. All decisions are to be completed individually and interaction with other participants is strictly PROHIBITED. Thank you for your cooperation.
Each person will receive a $5 show-up payment for participating. In addition, you can receive additional compensation based on the decision(s) that are made in the decision task described below. After the task is complete, you will be privately paid the amount of money you have earned. Upon completions of the decision task, please remain quietly seated in your carrel until you have been paid.
1.1.1 The decision task
You will be participating in a 2-person decision task. Each person will be randomly and anonymously paired with another person in the lab. In each of the 2-person decision making pairs, one person will be randomly assigned the role of PLAYER A and the other person will be randomly assigned the role of PLAYER B. You will remain in your assigned role for the entire session. The earnings of each Player will depend on the decision(s) he/she makes, and/or the decision(s) of the Player with whom they are paired. A brief outline of steps of the decision task will first be provided, followed by a detailed description of each step and the corresponding earnings for Player.
Step 1: PLAYER A begins by first choosing IN or OUT
-
If PLAYER A chooses OUT, the task ends
-
If PLAYER A chooses IN, then the task proceeds to Step 2
Step 2: PLAYER A might privately learn some payoff information that was initially unknown to both players. If PLAYER A does learn the information, the PLAYER A will then have an opportunity to convey the information to PLAYER B. Then the task will proceed to Step 3.
Step 3: PLAYER B chooses between RIGHT or LEFT, and the task ends
A full description of each step and the corresponding earnings for Player follows:
-
1.
PLAYER A first chooses between IN or OUT.
-
If PLAYER A chooses OUT, then the decision task ends. PLAYER A will receive $6 and PLAYER B will receive $2.
-
If PLAYER A chooses IN, the task proceeds to step (2) where PLAYER A might privately learn the unknown information, and then have an opportunity to convey that information to PLAYER B. After step (2), the task will proceed to step (3) where PLAYER B will then be asked to decide between RIGHT or LEFT.
-
-
2.
I postpone the details about the information that PLAYER A can possible learn, and convey to PLAYER B until after step (3) is described. Describing step (3) first will help clarify step (2).
-
3.
If PLAYER A chooses IN, at step (1), then PLAYER B must choose between RIGHT or LEFT.
-
If PLAYER B chooses RIGHT, then the decision task ends. PLAYER A will receive $10 and PLAYER B will receive $4.
-
If PLAYER B chooses LEFT, then the decision task ends and PLAYER A will receive $X and PLAYER B will receive $6. There is a 50 % chance that X \(=\) $0 and a 50 % chance that X \(=\) $6. That is, X \(=\) $0 and X \(=\) $6 are equally likely.
-
NOTE: When the decision task begins, neither PLAYER A nor PLAYER B knows the value of X. Therefore, PLAYER A does not know the value of X when he/she decides between IN or OUT in step (1).
Back to the description of step (2):
-
2.
If PLAYER A chooses IN, there is an 80 % chance that PLAYER A will privately learn the value of X, and a 20 % chance that PLAYER A will not privately learn the value of X.
-
If PLAYER A does learn the value of X (80 % chance), then PLAYER A must then decide whether or not to convey the value of X to PLAYER B before PLAYER B makes his/her decision in step (3).
-
If PLAYER A does convey the value of X, then PLAYER B will know the value of X before he/she decides between RIGHT or LEFT in step (3).
-
If PLAYER A does not convey the value of X, then PLAYER B will not know the value of X before he/she decides between RIGHT or LEFT in step (3).
-
-
If PLAYER A does not learn the value of X (20 % chance), then PLAYER A will not have an opportunity to convey the value of X to PLAYER B. The task will proceed to step (3) where PLAYER B will then choose between RIGHT or LEFT without knowing the value of X.
-
If PLAYER A chose to convey the value of X, then when PLAYER B makes his/her decision in step (3), the following message will appear on PLAYER B’s screen:
“PLAYER A has chosen to convey the value of X to you”
“The value of X is: [actual value of X]”
If either (a) PLAYER A did not learn the value of X after choosing IN, or (b) PLAYER A did learn the value of X but chose not to convey the value of X, then when it is time for PLAYER B to make his/her decision in step (3), the following message will appear on PLAYER B’s screen:
“The value of X remains unknown”
Payoff Table:
The table below summarizes the earnings of each Player for each of the possible outcomes in the decision task:
DECISION OUTCOME | Earnings of PLAYER A | Earnings of PLAYER B |
|---|---|---|
PLAYER A chooses OUT | $6 | $2 |
PLAYER A first chooses IN and then: | ||
PLAYER B chooses RIGHT | $10 | $4 |
PLAYER B chooses LEFT | $X | $6 |
There is a 50 % chance X = 0 and a 50 % chance X = 6 | ||
Each person will participate in this decision making task ONE time. After the task has ended, the decision(s) of each Player and the corresponding earnings of each Player will be revealed to both Players. Additionally, the value of X will be revealed to both PLAYER A and PLAYER B regardless of the decisions made in the task. You will then be asked to fill out a short questionnaire that will take about 3 min to complete. Your answers to the questionnaire are confidential and will not be shared with any other participants. After completion of the questionnaire, an Experimenter will then come by and privately pay you your total experimental earning which equals your earnings from the decision task PLUS the $5 show-up payment. After you have been paid, you may quietly exit the lab.
1.2 Appendix B.2: Sample screen shots
Player A’s Initial In/Out Decision

Player A’s Conditional Convey/Not Convey Decision

Player B’s Conditional Left/Right Decision (X Known)

Player B’s Conditional Left/Right Decision (X Unknown)

Rights and permissions
About this article
Cite this article
Cardella, E. Exploiting the guilt aversion of others: do agents do it and is it effective?. Theory Decis 80, 523–560 (2016). https://doi.org/10.1007/s11238-015-9513-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-015-9513-0