Flow assignment (FA) and capacity and flow assignment (CFA) problems for survivable overlay multicasting in dual homing networks

Abstract

Overlay multicasting providing live streaming services became crucial service in contemporary Internet. In this paper, we focus on applying the overlay multicasting for delivering of critical data that require to be transmitted safely, intact and with as little delay as possible. To improve survivability of the overlay multicasting, we propose to use dual homing approach, i.e., each peer is connected to the overlay by two separate access links. We consider the following network failures: overlay link failure, uploading node failure and ISP interconnection failure. The main goal of our experiments is to determine the additional cost of providing survivability to the overlay multicasting network with dual homing technology for both flow assignment and capacity and flow assignment problems. Our studies indicate that the additional survivability requirements do not have a substantial impact on the overlay multicasting system expressed as streaming cost or network cost.

1 Introduction

Nowadays, we are observing a rapid growth in popularity of multimedia streaming in the Internet [1]. To emphasize the growing popularity of various video streaming services, we need to quote [2] where the authors claim that Video on Demand traffic will triple and Internet TV will be increased 17 times by 2015. The total share of all forms of video (already mentioned) and P2P will grow continuously to make up approximately 90 % of all global consumer traffic in the next 3 years. Useful services like Video on Demand, internet radio, IPTV and high definition video or audio streaming very often require a lot of bandwidth, which can be costly [3]. The main advantages of using the overlay network approach are scalability, adaptability, low deployment cost, and optimal content distribution [4], which are crucial to meet that demand. The overlay multicasting technology is based on a multicast delivery tree consisting of peers (end hosts). The overlay multicasting can transmit either streaming content with additional requirements like bit rate etc. or data files [5]. We are addressing a situation where the overlay system is static (peers stay connected to the system for a long time), e.g., Content Delivery Network (CDN) like Akamai Technologies.

The problem of optimum network design in order to satisfy a predefined set of system requirements (such as traffic demands, timing constraints, reliability issues, desired level of security, quality of service and so on) while minimizing the total network cost, arises in many application areas, especially in computer and telecommunication networks. We apply the overlay multicasting in a dual homing architecture to improve the network survivability. One of main assumptions of our work is that the overlay multicasting is applied to deliver crucial information that needs to be transferred fast and intact, e.g., hurricane warnings, financial information, critical updates in large IT systems etc. To meet that demand we propose a survivable overlay multicasting approach. This is motivated by the fact, that nowadays we can observe growing interest in cost effective and reliable streaming services. Dual homing topology requires that all hosts (nodes) have two disjoint links (homes) to the network. Network protection is provided because of link redundancy. The main contribution of the paper consists of: (i) Integer Linear Programming (ILP) formulations of survivable overlay multicasting systems with additional survivability constraints using dual homing architecture for flow assignment problem. (ii) ILP formulations of survivable overlay multicasting systems with additional survivability constraints using dual homing architecture for capacity and flow assignment problem. (iii) Numerical experiments based on ILP models showing results for both problems and performance of various survivability constraints.

The rest of this paper is organized in the following way. In Sect. 2, we present previous research on overlay multicasting and dual homing. Section 3 introduces the concept of survivable overlay multicasting based on the dual homing method. In Sect. 4, we formulate ILP models for flow assignment problem. Moreover, numerical experiments and their results are presented. Analogously, Sect. 5 introduces ILP models for capacity and flow assignment along with experiments results. Finally, we conclude this paper in Sect. 6.

This paper is an extended version of the paper [6], presented at 4th International Workshop on Reliable Networks Design and Modeling RNDM 2012, held in St. Petersburg on October 3–5, 2012. This extended paper contains the following new results. (i) A ILP formulations of survivable overlay multicasting in dual homing networks for capacity and flow assignment. (ii) Results and conclusions of extensive numerical experiments. To the best of our knowledge, this work is the first one that addresses the problem of CFA in overlay networks with dual homing protection. Note that the concept of overlay multicasting protection by dual homing has been introduced in our recent papers [6–8].

2 Related works

In this section, we present previous papers related to dual homing, overlay multicasting, and network survivability.

Dual homing is a subject of several articles. The authors of [9] created the multicast protection scheme based on a dual homing architecture where each destination host is connected to two edge routers. Under such an architecture, the two paths from the source of the multicast session to the two edge routers provide protection for the traffic from the source to the destination. This paper addresses the problem of offline optimization and authors’ protection scheme is applied in lower layers of ISO/OSI model resulting in less flexibility.

Another field of application for dual homing technology are self-healing ring networks [10, 11], where new network design methods and routing algorithms are designed and developed. An integer programming formulation and the NP-completeness of the problem is presented. In [12], the authors introduce a concept of partial protection for the multicast dual homing network and a new algorithm PAS for finding the best partial multicast protection tree is proposed. The authors claim that simulation results show that the PAS algorithm achieves performance very close to the computed lower bounds. The authors of [13] studied IP-over-WDM network survivability with a dual homing infrastructure. The paper focuses on a problem of adding survivability to IP WDM multicasting networks for both static and dynamic traffic. The authors created and evaluated coordinated protection design. A scalable multicast protection scheme based on the dual homing architecture was introduced in [14]. The solution proposed by the authors can be used to choose dynamically two edge routers for a multicast host. The authors of [15] addressed disjoint multipath routing in the dual homing network problem. An algorithm for constructing colored trees in dual-homing using colored trees is proposed.

Overlay multicast (application-layer multicast) [16] is a technology, which uses the overlay network topology, that enables multicast functionality for end hosts instead of routers. The authors propose a proactive tree recovery mechanism to make the overlay multicast resilient to peer failures. Simulations are used to prove that the proactive method can recover from node failures much faster than reactive methods. Authors of [17] deal with problem of modeling and optimization of maximum flow survivable overlay multicast with predefined routing trees. They present linear formulation derived from fractional tree packing problems based on predefined topologies, which may route multicast traffic. Moreover, heuristic searches dedicated to optimization of maximum flow survivable overlay multicast networks are designed and evaluated. In [18], the authors propose a novel protocol named Efficient Overlay Multicast Routing (EOMR), in which multilayer multicast methods are integrated and the conversion among these methods is performed dynamically. Moreover, a Multicast Address and Port Translation (MAPT) protocol is used to achieve low-level overlay forwarding in intermediate systems, while the application-level multicast can only be implemented in end systems. Authors claim the overhead of EOMR is relatively low while maintaining comparative forwarding performance to pure IP multicast protocols. The Virtual Direction Multicast (VDM), which aims to minimize network usage and disconnection time for video multicast applications on overlay networks, is proposed in [19]. Authors compared VDM against a Closest Node Multicast (CNM) protocol and simulation results show that our proposed technique VDM consistently outperforms CNM under different churn rates. The authors of [20] deal with a problem of joint optimization of 2-tier dual homing for NodeBs and RNCs in UMTS networks. They combined the optimization problems across the two tiers, mapped the joint dual homing optimization problem into a classical search problem, and used two metaheuristic techniques to solve the above problem. Results of the experiments reveal that the joint dual homing performs considerably better than individual dual homing that attacks NodeB level and RNC level separately and independently. In [21], the authors address the problem of network survivability in the context of anycast communications. To assure the network survivability, they use the single backup path approach. Authors formulate new ILP models to find the optimal paths for anycast and unicast connections, as well as to find the optimal location of replica servers. To test the proposed approach, they run extensive numerical experiments using CPLEX solver on four example network topologies with different scenarios of replica server count and the proportion between unicast and anycast traffic.

In our previous work [6], we proposed four different ILP models that allow us to create link, node, and ISP disjoint multicast trees. We introduced a Simulated Annealing (SA) algorithm for the considered optimization problem and compared it with optimal results provided by CPLEX solver. We also introduced several distributed tree construction strategies and conducted simulation experiments to investigate problems of providing survivability to both static and dynamic types of the network.

3 Survivability of overlay multicasting

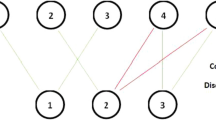
In this paper, we are studying the network survivability problem for dual homing architecture. In Fig. 1, we present a simple example to illustrate our concept.

Fig. 1

Simple overlay multicast scheme

There are two disjoint multicast trees A, B that connect 7 nodes—$a,b,c,d,e,f$, and g. In the case of tree $A$, nodes $a,d$ and $f$ are uploading nodes, while remaining ones are leafs. Term level is used to describe location of nodes in the multicast tree. For example, node $a$ is situated on first level of tree $B$, nodes $b$ and $e$ are on second level of tree $B$, while rest of the nodes are on third level.

The overlay multicasting is done in the application layer, i.e., end hosts are connected using the overlay network. Connections between peers are established as unicast connections over the underlying physical layer. Each peer is connected to the overlay by an access link. We propose to use the dual homing approach to protect the system against a failure of the access link. The main idea is to create two disjoint overlay multicasting trees guaranteeing that each of access links carries traffic of only one of the trees. Since each node has two, physically disjoint, access links (dual homing), it receives streaming data from both trees on two separate links. Note that, both access links should be placed separately along different physical paths. This follows mainly from the fact that if some links are physically routed together in a duct and a failure occurs (e.g., digging, cut) both links are affected simultaneously [22]. In case of failure of one of access links, the node still is connected to the stream. Moreover, it can upload the data to succeeding peers located in the multicast tree.

The overlay system we consider is assumed to be protected against the following types of failures:

• Overlay link failure it comprises breakdown of a link between two nodes (both directed links between the node pair are down),

• Uploading node failure this failure impacts all successors of the failed peer in the tree,

• ISP link failure all overlay links between peers of first ISP and the second ISP are not available.

4 Flow assignment (FA)

In the flow assignment problem, for the given set of demands (described by: demand volume, origin node, destination node, and optionally candidate paths) the goal is to select the routing, i.e., determine network paths used for transmission of demands. The most important constraint is related to the limited link capacity. Since the network is fixed, the total flow on each link cannot exceed the given physical link capacity. In this section, we address the flow assignment problem in the context of survivable overlay multicasting in dual homing networks.

4.1 ILP models

The notation as in [23] is used to formulate the problem. ILP models presented below are based on the formulation shown in [7]. However, the models are enhanced with additional survivability constraints following from considered failure scenarios and were introduced in [6]. Let indices $v,w=1,2,{\ldots },V$ denote peers—nodes of the overlay network. There are $K$ peers (clients) indexed $k=1,2,{\ldots },K$ that want to receive the data stream and are not root nodes in any trees. Index $t=~1,2,{\ldots },T$ denotes streaming trees. In our work, we assume that $T=2$. Nodes are situated on levels $l=1,2,{\ldots },L$ in the multicast trees. That gives us possibility to set a limit on the maximum depth of the tree. Setting this additional constraint gives us the possibility to improve the Quality of Service (QoS) parameters of the overlay multicasting, e.g., transmission delay and network reliability. If node $v$ is the root of the tree $t$, then $r_{vt}=1$, otherwise $r_{vt}=0$. Constant $c_{wv}$ denotes the streaming cost on an overlay link $(w,v)$ that can be interpreted as a network delay or a transmission cost.

We introduce constant $\tau (v)$, which adds a virtual node associated with the node $v$. Together they form a primal node. Every primal node has in fact four capacity parameters—constants $u_{v}$ and $d_{v}$ are respectively upload and download capacity of the node $v$ and constants $u_{\tau (v)}$ and $d_{\tau (v)}$ are parameters of the virtual node $\tau (v)$. We propose additional constraints to protect not only from the overlay link failure, but also to protect against uploading node and ISP interconnection link failures.

Figure 2 depicts an example of the dual homing modeling. Dual homes are marked with a pattern of sequential lines and dots. It is shown that streaming trees are using different connections to nodes. The objective function in the FA problem is the streaming cost (cost of all multicast trees).

Fig. 2

Modeling dual homing

4.1.1 Level streaming cost—no survivability (LSC-NS)

First, we formulate a basic ILP model that does not include additional survivability constraints. To model overlay multicasting we use a set of binary variables. First variable $x_{vt}$ is 1, if an access link of node $v$ is used to upload or download flow of the multicast tree $t$; 0, otherwise. Variable $x_{wvt}$ is set to 1, if a link from node $w$ to node $v$ (no other peer nodes in between) is established in the multicast tree $t$; 0 otherwise. Finally, variable $x_{wvtl}$, is 1 when in the multicast tree $t$ there is an overlay link $(w,v)$ (no other peer nodes in between) and $w$ is located on level $l$ of the tree $t$; 0 otherwise.

Indices

$v,w,b=1,2,{\ldots },V$ :

overlay nodes (peers)

$k=1,2,{\ldots },K$ :

receiving nodes (peers)

$t=1,2,{\ldots },T$ :

streaming tree index

$l=1,2,{\ldots },L$ :

levels of the tree

Constants

$d_{v}$ :

download capacity of node $v$ (kbps)

$u_{v}$ :

upload capacity of node $v$ (kbps)

$r_{vt}$ :

= 1, if node $v$ is the root (streaming node) of tree $t$; 0, otherwise

$q$ :

the streaming rate (kbps)

$c_{wv}$ :

streaming cost on overlay link from node $w$ to node $v$

$M$ :

large number

Variables

• $x_{wvtl} = 1$, there is an overlay link $(w,v)$ (no other peer nodes in between) in multicast tree $t$ and $w$ is located on level $l$ of tree $t$; 0, otherwise (binary)

• $x_{wvt} = 1$, if link from node $w$ to node $v$ (no other peer nodes in between) is in multicast tree $t$; 0, otherwise (binary)

• $x_{vt} = 1$, if access link of node $v$ is used to download or upload flow of multicast tree $t$; 0, otherwise (binary)

Objective

$$\begin{aligned} \hbox {Minimize}\quad {\sum }_w {\sum }_v {\sum }_{t} x_{wvt} c_{wv} \end{aligned}$$

(1)

Constraints

$$\begin{aligned}&{\sum }_{w} {\sum }_{t} {\sum }_{l} x_{wvtl} =0\quad v=1,2,\ldots ,V\quad r_{vt} =1\end{aligned}$$

(2)

$$\begin{aligned}&{\sum }_{k} x_{wkt1} q\le u_{w} r_{wt} \quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned}&{\sum }_{w} {\sum }_l x_{wktl} =x_{kt} \quad k=1,2,\ldots ,K\quad t=1,2,\ldots ,T\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}&x_{wvt(l+1)} \le {\sum }_{b} x_{bwtl} \quad v=1,2,\ldots ,V\quad w=1,2,\ldots ,V\nonumber \\&\quad t=1,2,\ldots ,T\quad l=1,2,\ldots ,L-1.\end{aligned}$$

(5)

$$\begin{aligned}&{\sum }_{t} {\sum }_{l} x_{vvtl} =0\quad v=1,2,\ldots ,V\end{aligned}$$

(6)

$$\begin{aligned}&{\sum }_{l} x_{wvtl} \le x_{wvt} \quad v=1,2,\ldots ,V\quad w=1,2,\ldots ,v\nonumber \\&\quad t=1,2,\ldots ,T\end{aligned}$$

(7)

$$\begin{aligned}&{\sum }_{w} {\sum }_{t} x_{wvt} q\le d_{v} \quad v=1,2,\ldots ,V\end{aligned}$$

(8)

$$\begin{aligned}&{\sum }_{v} {\sum }_{t} x_{wvt} q\le u_{w} \quad w=1,2,\ldots ,V\end{aligned}$$

(9)

$$\begin{aligned}&{\sum }_{w} x_{wvt} +{\sum }_{w} x_{vwt} \le M\quad x_{vt} v=1,2, \ldots ,V\nonumber \\&\quad t=1,2,\ldots ,T\end{aligned}$$

(10)

$$\begin{aligned}&{\sum }_{t} x_{vt} =1v=1,2,\ldots ,V \end{aligned}$$

(11)

Since in overlay multicasting, the root node does not receive any data (it is located on the first level of the tree) we add to the model constraint (2). Constraint (3) assures that only the root node is allowed to upload on the first level of the tree. Condition (4) binds variables $x_{wvtl}$ and $x_{vt}$. Constraint (5) assures that the node can upload data on the level ($l+1$) only when it is downloading on the level $l$. We add condition (6) to ensure that internal flow of the node equals zero. Constraint (7) forces that a connection between $(w,v)$ denoted by variable $x_{wvt}$ exists in the tree $t$, when there is a transmission between nodes $(w,v)$ on any level $l$ of the tree $t$. This constraint guarantees that in each tree there is at most one transmission per overlay link $(w,v)$. (8) and (9) are respectively the upload and download capacity constraints. Condition (10) defines the $x_{vt}$ variable. Finally, constraint (11) assures, that multicast trees are separate—each node $v$ (access link) can only be used in one tree $t$.

Model (1)–(11) is a basic model of overlay multicasting in dual homing networks. Below we introduce additional constraint to formulate new survivability models taking into account the following types of network failures:

• Overlay link failure,

• Uploading node,

• ISP link failure.

4.1.2 Level streaming cost—link disjoint (LSC-LD)

Constants (additional)

$\tau (v)$ :

index of node associated with node $v$ (virtual node)

Constraints (1)–(11) and

$$\begin{aligned}&x_{vt} +x_{\tau \left( v \right) t} =1\quad v=1,2,\ldots ,V\quad t=1,2,\ldots ,T\end{aligned}$$

(12)

$$\begin{aligned}&{\sum }_{t} x_{v\tau \left( v \right) t} =0\quad v=1,2,\ldots ,V \end{aligned}$$

(13)

Survivable constraints (12), (13) state, that only one node from the primal node can belong to tree $t$ and there cannot be connection within primal node, e.g., between node $v$ and $\tau (v)$. Those constraints ensure that every primal node is connected to both multicast trees and each tree is using different access link of the primal node e.g. represented by nodes $v$ and $\tau (v)$. Note that such a configuration protects the system against a single overlay link failure.

Below we introduce a new ILP model related to a node disjoint dual homing network. To be able to denote if a particular node is uploading in a given multicast tree, new variable $y_{vt}$ is introduced.

4.1.3 Level streaming cost—node disjoint (LSC-ND)

Variables (additional)

• $y_{vt} = 1$, if node $v$ is uploading in multicast tree $t$; 0,otherwise (binary)

Constraints (1)–(13) and

$$\begin{aligned}&{\sum }_{v} x_{wvt} \le My_{wt} ,\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T\end{aligned}$$

(14)

$$\begin{aligned}&y_{wt} \le {\sum }_{v} x_{wvt} ,\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T\end{aligned}$$

(15)

$$\begin{aligned}&{\sum }_{t} (y_{vt} +y_{\tau \left( v \right) t} )\le 1,\quad r_{vt} \ne 1\quad r_{\tau \left( v \right) } \ne 1\quad v=1,2,\ldots ,V\nonumber \\ \end{aligned}$$

(16)

Constraints (14)–(15) are used to define the new variable $y_{vt}$. Constraint (16) assures that from nodes forming the primal node at most only one node can upload data in the multicast tree.

Lastly, we introduce an ILP model that addresses the problem of ISP link failure.

4.1.4 Level streaming cost—ISP disjoint (LSC-ID)

Indices (additional)

$p,m =1,2,{\ldots },P$ :

Internet Service Providers (ISPs)

Constants (additional)

• $\alpha (v,p) = 1$, if node $v$ belongs to ISP $p$; 0, otherwise

Variables (additional)

• $z_{pmt} =1,$ if in multicast tree $t$ there is at least one link from a node located in ISP $p$ to a node located in ISP $m$ or in opposite direction; 0, otherwise (binary)

Constraints (1)–(13) and

$$\begin{aligned}&{\sum }_{w:\alpha \left( {w,p} \right) =1} {\sum }_{v:\alpha \left( {v,m} \right) =1} \left( {x_{wvt} +x_{vwt} } \right) \le Mz_{pmt}\nonumber \\&\quad p=1,2,\ldots ,P \nonumber \\&\quad m=1,2,\ldots ,P\quad p\ne m\quad t=1,2,\ldots ,T \end{aligned}$$

(17)

$$\begin{aligned}&z_{pmt} \le {\sum }_{w:\alpha \left( {w,p} \right) =1} {\sum }_{v :\alpha \left( {v,m} \right) =1} \left( {x_{wvt} +x_{vwt} } \right) \nonumber \\&\quad p=1,2,\ldots ,P \nonumber \\&\quad m=1,2,\ldots ,P\quad p\ne m \quad t=1,2,\ldots ,T \end{aligned}$$

(18)

$$\begin{aligned}&{\sum }_{t} z_{pmt} \le 1\quad p=1,2,\ldots ,P\quad m=1,2,\ldots ,P \end{aligned}$$

(19)

Note that the ISP link failure includes the failure of both directed ISP links, i.e. $(p,m)$ and $(m,p)$. Constraints (17)–(18) define the new variable $z_{pmt}$, while the last condition (19) assures that each ISP link is applied in at most one tree.

The considered optimization problem is complex and NP-hard, since it can be reduced to the hop-constrained minimum spanning tree problem, which is known to be NP-hard [25]. Due to that fact, branch-and-bound or branch-and-cut methods have to be applied to obtain optimal solution.

4.2 Simulation results

The main goal of our experiments is to determine the additional cost of providing survivability to the overlay multicasting network with dual homing technology. We randomly generated networks with 10 and 20 primal nodes and two disjoint trees. Results for network with 50 nodes were achieved only for the heuristic algorithm proposed in [6]. To solve ILP models in an optimal way, we use CPLEX solver v12.4 [14]. We created at random networks with link costs in range 1–50, streaming rates $q =128$, 256, 384, 512 kbps, level limit $L$ in range from 2 to 5 and with asymmetric nodes (1 Mbps/512 kbps, 2 Mbps/512 kbps, 6 Mbps/512 kbps, 10/1 Mbps, 20/1 Mbps, 50/2 Mbps). Number of ISPs $P$ was set to 5. We assume that node $v=1$ is the streaming node for tree $t=1$ and node $\tau$(1) is the streaming node for tree $t=2$. To achieve results in a reasonable time, we set timemax value to 3600 s, limiting the execution time of CPLEX. The goal of numerical experiments is threefold:

• Checking how the streaming rate q and different L values would affect the overall streaming cost,

• Checking how the size of the network and given survivability scenario would affect the processing time of CPLEX and the gap to optimality.

• Checking the influence of introducing survivability to the overlay multicasting.

The first goal of the experiments was to test how the streaming rate $q$ and the $L$ value affect the streaming cost for network with 10 primal nodes and various survivability scenarios. In Fig. 3, we can observe, that the streaming cost grows with increase of the streaming rate. An opposite dependence can be noticed when increasing the $L$ level limit (Fig. 4). The experiment was conducted for $L$ values in range from 2 to 5, but for $L=2$ given network was infeasible for all survivability scenarios. Node disjoint survivability is the most expensive one in terms of the streaming cost in both experiments. This is implied by the fact that ND requirements reduce solution space significantly and consequently the cost of feasible solutions grows.

Fig. 3

Streaming cost as a function of steaming rate $q$ for network with 10 primal nodes and $L=3$—the FA problem

Fig. 4

Streaming cost as a function level limit $L$ for network with 10 primal nodes and $q=512$ kbps—the FA problem

In Table 1, we present results related to the second goal of the experiments. For networks with 10 primal nodes, CPLEX was able to find the optimum in a short period of time—1, 3, 7, and 10 s for NS, LD, ND and ID survivability scenarios respectively.

Table 1 Average cplex processing time and optimality gap for networks with 10 and 20 primal nodes and different survivability scenarios—the FA problem

In case of networks with 20 primal nodes, CPLEX processing time was much larger, from 1384 s for NS scenario to 3025 s for ISP Disjoint survivability. Note that, all CPLEX results presented for the FA problem are optimal.

Finally, we address the third goal of the experiments—Tables 2 and 3 report results showing the comparison between all four survivability scenarios. Both Tables illustrate dependencies, that are in harmony with our previous conclusions—for all survivability scenarios and network parameters, streaming cost is increasing with the streaming rate $q$ and decreasing with more number of levels $L$ in the multicast tree. 12 unique experiments were conducted for each network size (combination of 3 different streaming rates $q$ and 4 $L$ values). Column Diff shows the percentage difference of the particular survivability scenario in comparison to the basic model without survivability constraints. The relative additional cost of providing additional survivability for 10-node and 20-node networks was: 22.8 and 21.7 % in the case of the link disjoint constraint; 34.3 and 35.5 % for the node disjoint constraint; 33.3 and 40.4 % in the case of the ISP disjoint constraint. The cost of providing ISP disjoint multicast trees grows with the ratio of the number of nodes to the number of ISPs.

Table 2 Additional cost of providing survivability for all types of network with 10 primal nodes—the FA problem

Table 3 Additional cost of providing survivability for all types of network with 20 primal nodes—the FA problem

5 Capacity and flow assignment (CFA)

The CFA problem consists in finding such a multicommodity flow and capacity modules allocation that satisfies conditions arising from network topology, traffic matrix, etc. [23]. In this section, we focus on the CFA problem in the context of survivable overlay multicasting in dual homing networks. In more detail, with a given set of ISPs and candidate links with specified download and upload capacities along with cost (Euro/month) we try to minimize overall network cost understood as total cost of all candidate access links assigned to network nodes. The solution has to meet the requirement of not exceeding given maximum streaming cost.

Figure 5 depicts an example of the capacity and flow assignment problem. The main difference between the FA and CFA is an additional phase, where ISPs and the corresponding candidate access links are assigned to network nodes. For example, ISP 1 and candidate link 2 was assigned to node $a$, ISP 2 and candidate link 3 to node $\tau (a)$ etc.

Fig. 5

Capacity and flow assignment scheme

Below we introduce four novel ILP models based on the corresponding ones for the flow assignment problem.

5.1 ILP models

5.1.1 CFA—no survivability—(CFA-NS)

Firstly, analogously to the FA models, we describe basic ILP model with no survivability constraints. We add indice $a=1,2{\ldots },A_{p}$, which denotes candidate link types for given ISP $p$. Constants $d_{ap}$ and $u_{ap}$ are respectively download and upload capacities of access link type $a$ of ISP $p$. Parameter $n$ allows us to set an upper bound on the maximum streaming cost of all overlay links. Constant $e_{vp}$ is set to 1, if ISP $p$ is available for node $v$; otherwise $e_{vp}=0$. Additional binary variable $g_{vap}$ is set to 1, when candidate access link $a$ of ISP $p$ is selected for node $v$, otherwise it is set to 0. The objective function for the CFA problem (20) is the overall cost of all access links assigned to the nodes in the network (network cost).

Indices (additional)

$a=1,2{\ldots },A_{p}$ :

candidate link types for ISP $p$

Constants (additional)

$d_{ap}$ :

download capacity of access link type $a$ of ISP $p$ (kbps)

$u_{ap}$ :

upload capacity of access link type $a$ of ISP $p$ (kbps)

$\xi _{ap}$ :

cost of access link type $a$of ISP $p$ (Euro/month)

$n$ :

maximum overall streaming cost

$e_{vp}$ :

= 1, if ISP $p$ is available for node $v$; 0, otherwise

Variables (additional)

• $g_{vap} =1$, if link type $a$ of ISP $p$ is selected for node $v$; 0, otherwise (binary)

Objective

$$\begin{aligned} \hbox {minimize}\quad {\sum }_{v} {\sum }_{a} {\sum }_{p} g_{vap} \xi _{ap} \end{aligned}$$

(20)

Constraints (2), (4)–(7), (10)–(11) and

$$\begin{aligned}&{\sum }_k x_{wkt1} q\le {\sum }_{a} {\sum }_{p} u_{ap} g_{wap} r_{wt} \quad w=1,2,\ldots ,V\nonumber \\&\quad t=1,2,\ldots ,T\end{aligned}$$

(21)

$$\begin{aligned}&{\sum }_{w} {\sum }_{t} x_{wvt} q\le {\sum }_{a} {\sum }_{p} d_{ap} g_{vap} \quad v=1,2,\ldots ,V \end{aligned}$$

(22)

$$\begin{aligned}&{\sum }_{v} {\sum }_{t} x_{wvt} q\le {\sum }_{a} {\sum }_{p} u_{ap} g_{wap} \quad w=1,2,\ldots ,V \end{aligned}$$

(23)

$$\begin{aligned}&{\sum }_{p} {\sum }_{a} g_{vap} e_{vp} =1\quad v=1,2,\ldots ,V\end{aligned}$$

(24)

$$\begin{aligned}&{\sum }_{w} {\sum }_{v} {\sum }_{t} x_{wvt} c_{wv} \le n \end{aligned}$$

(25)

Constraints (21)–(23) are based on the corresponding constraints from the LSC-NS model. Constraint (24) assures that the candidate link $a$ is chosen only from ISP $p$ available for node $v$. Constraint (25) sets the upper bound on the overall streaming cost of all the links in the multicast trees.

5.1.2 CFA—link disjoint (CFA-LD)

The second ILP model provides Link Disjoint survivability. It utilizes already mentioned constant $\tau (v)$.

Constraints (2), (4)–(7), (10)–(11), (12), (13), (20)–(25) and

$$\begin{aligned} {\sum }_{a} \left( {g_{vap} +g_{\tau \left( v \right) ap} } \right) \le 1\quad v=1,2\ldots ,V\quad p=1,2\ldots ,P\nonumber \\ \end{aligned}$$

(26)

Condition (26) assures, that both nodes $v$ and $\tau (v)$ belong to different ISPs. That constraint is crucial for the survivability in the CFA problem. When both nodes are in the same ISP, failure of a single Internet provider can fully disconnect primal node from the network. An important difference between the FA and the CFA problems is that in the FA all the nodes are already assigned to a specific ISP, whereas in the CFA assignment ISPs to nodes is a part of the optimization problem.

5.1.3 CFA—node disjoint (CFA-ND)

Additional survivability constraints for providing Node Disjoint survivability are the same as (14)–(16) in LSC-ND model. Accordingly, we introduce variable $y_{vt}$ to the model.

Constraints (2), (4)–(7), (10)–(11), (12), (13), (20)–(26)

5.1.4 CFA—ISP disjoint (CFA-ID)

Finally, the ILP model providing ISP disjoint survivability is presented. Variable $g_{vp}$ is set to 1 if node $v$ belongs to ISP $p$, otherwise it equals 0. $g_{wvpm}$ equals 1, if pair of nodes $w$ and $v$ belong to IPSs $p$ and $m$.

Variables (additional)

• $g_{vp}=1$, if node $v$ belongs to IPS $p$; 0, otherwise (binary)

• $g_{wvpm}=1$, if pair of nodes $w$ and $v$ belong to ISPs $p$ and $m$, respectively; 0, otherwise (binary)

Constraints (2), (4)–(7), (10)–(11), (12), (13), (20)–(26) and

$$\begin{aligned}&{\sum }_{a} g_{vap} =g_{vp} \quad v=1,2,\ldots ,V\quad p=1,2,\ldots ,P\end{aligned}$$

(27)

$$\begin{aligned}&g_{wp} \!+\!g_{vm} \le 1\!+\!g_{wvpm} \quad p\!=\!1,2,\ldots , P\quad m\!=\!1,2,\ldots P \nonumber \\&\quad v=1,2,\ldots ,V\quad w=1,2,\ldots ,V \end{aligned}$$

(28)

$$\begin{aligned}&g_{wvpm} \le g_{wp} \quad p=1,2,\ldots ,P\quad m=1,2,\ldots P \nonumber \\&\quad v=1,2,\ldots ,V\quad w=1,2,\ldots ,V \end{aligned}$$

(29)

$$\begin{aligned}&g_{wvpm} \le g_{vm} \quad p=1,2,\ldots ,P\quad m=1,2,\ldots P \nonumber \\&\quad v=1,2,\ldots ,V\quad w=1,2,\ldots ,V \end{aligned}$$

(30)

$$\begin{aligned}&g_{wvpm} +x_{wvt} \le 1+z_{pmt} \quad p=1,2,\ldots ,P\nonumber \\&\quad m=1,2,\ldots P \quad p\ne m\quad v=1,2,\ldots ,V\nonumber \\&\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T \end{aligned}$$

(31)

$$\begin{aligned}&2z_{pmt} \le {\sum }_w {\sum }_{v} (g_{wvpm} +x_{wvt} )\quad p=1,2,\ldots ,P\nonumber \\&\quad m=1,2,\ldots P \quad p\ne m\quad v=1,2,\ldots ,V\nonumber \\&\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T \end{aligned}$$

(32)

$$\begin{aligned}&g_{wvmp} +x_{wvt} \le 1+z_{pmt} \quad p=1,2,\ldots ,P\nonumber \\&\quad m=1,2,\ldots P \quad p\ne m\quad v=1,2,\ldots ,V\nonumber \\&\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T \end{aligned}$$

(33)

$$\begin{aligned}&2z_{pmt} \le {\sum }_w {\sum }_{v} (g_{wvmp} +x_{wvt} )\quad p=1,2,\ldots ,P\nonumber \\&\quad m=1,2,\ldots P \quad p\ne m\quad v=1,2,\ldots ,V\nonumber \\&\quad w=1,2,\ldots ,V\quad t=1,2,\ldots ,T \end{aligned}$$

(34)

Constraint (27) defines a new variable $g_{vp}$. Analogously, set of constraints (28)–(30) define new variable $g_{wvpm}$. Finally, constraints (31)–(34) are used to define the new variable $z_{pmt}$. Note that (32)–(34) are introduced because of the fact, that $z_{pmt}$ needs to be 1 in case when there is connection between ISPs $p$ and $m$ and also in the opposite direction.

5.2 Simulation results

For simulations related to the CFA problem, we used networks with 10 primal nodes generated for the FA problem. We did not use networks with 20 and 50 primal nodes, because the CFA problem is more complex than the FA problem and in result, we were not able to achieve even feasible solutions for those networks. We chose the same values of streaming rate $q$, level limit $L$ and range of link costs $c_{wv}$. Additionally, maximum overall streaming cost parameter equals $n=50$, 75, 100, 125, 150 and 200. We created 5 ISPs, based on the current offer of ISPs in Poland (Orange, Netia, Dialog, Multimedia, UPC), each with 6 candidate link types with different download and upload capacities as well as cost expressed in Euro per month. Overall, we generated 96 networks (combination of 4 different streaming rates $q$, 4 $L$ values and 6 maximum streaming cost limits $n$) for each survivability scenario. This time we set timemax value for 3 h (10,800 s), because the CFA problem is much more complex and harder to solve than the FA.

As in the case of FA simulation, there were three main goals of the experiments:

• Checking how the different values of streaming rate $q$, level limit $L$ and streaming cost limit $n$ would affect the network cost for different survivability scenarios,

• Checking how given survivability scenario would affect the processing time of CPLEX and gap to optimality.

• Checking the influence of introducing survivability to the overlay multicasting for the CFA problem.

The first goal was to test influence of different values of streaming rate $q$, level limit $L$ and streaming cost limit $n$ on network cost. Figures 6, 7, and 8 depict result of our simulation experiments. We can observe that the overall network cost grows with increase of the streaming rate (Fig. 6) and drops with increase of the $L$ value (Fig. 7) for networks with and without survivability constraints. Those results are in harmony with our previous observations related to the FA problem. With the increase in limit of the maximum overall streaming cost $n$, network cost is dropping. For every network there is a point, from which increasing the $n$ value does not decrease the objective function (Fig. 8).

Fig. 6

Network cost as a function of steaming rate $q$ for network with 10 primal nodes, $L=3$ and $n=125$—the CFA problem

Fig. 7

Network cost as a function of level limit $L$ for network with 10 primal nodes, $q=512$ and $n=125$—the CFA problem

Fig. 8

Network cost as a function of maximum streaming cost $n$ for network with 10 primal nodes, $L=3$ and $q=512$—the CFA problem

Additionally, in Table 4 we present number of feasible solutions (meaning there exists solution that satisfies all of the constraints) for scenarios with and without survivability. We can observe, that survivable scenarios achieved much lower number of infeasible solutions—up to 48 of total number of 96 generated networks. Additional survivability constraints cause strongly constrained networks (e.g. low $L$ limit or $n$ maximum streaming cost) to become infeasible.

Table 4 Number of feasible solutions for NS, LD, ND and ID models—the CFA problem

In Table 5, we present results for the experiment testing how given survivability scenario is affecting the processing time of CPLEX and gap to optimality for the CFA problem. Comparing to the FA problem, the processing time is much larger for network with 10 primal nodes—hours instead of seconds. That proves high complexity of the CFA problem. Analogously, optimality gap is bigger—from $\sim$1 % for NS, LD and ND scenarios to 4.5 % for ISP disjoint network.

Table 5 Average cplex processing time and optimality gap for network with 10 primal nodes and different survivability scenarios—the CFA problem

Analogously to the experiments related to the FA problem, we summarize with Table 6, where all the results of research on the CFA problem are gathered. Note that results are averaged for all the overall streaming cost limit $n$ values. Network cost is similarly correlated with streaming rate $q$ and level limit $L$ as the streaming cost (the FA). Table 6 depicts the average difference over 48 experiments (for which we were able to achieve feasible results for all scenarios) of the particular survivability scenarios in comparison to the basic model without survivability constraints in terms of the network cost. The additional cost of providing link disjoint survivability was 5 % of the network cost, for the node disjoint constraints that value was 5.5 % and for the ISP disjoint constraints it was 6.8 %. These values are significantly lower than those from FA problem. This can be explained by the fact that survivability constraints affect directly the overall streaming cost (by forbidding connections between certain ISPs), while their influence on the network cost (cost of physical links in the network) is only indirect (through $n$ parameter). ISP disjoint constraints impact strongly the process of choosing the ISPs and, in effect, the cost of candidate links. That is the reason why additional cost of providing ISP disjoint constraints is the highest for CFA problem, where candidate links are assigned to network nodes.

Table 6 Additional cost of providing survivability for all types of network with 10 primal nodes–the CFA problem

6 Conclusion

In this paper, we addressed the problem of survivable overlay multicasting in dual homing networks. Four novel ILP models of survivable overlay multicasting systems with additional survivability constraints using dual homing architecture for the capacity and flow assignment problem were introduced. The main goal of experiments was to examine how the additional survivability constraints influence the overall streaming cost (flow assignment problem) and the network cost (capacity and flow assignment problem). Moreover, experiments testing the impact of streaming rate and number of levels on the objective functions were conducted. The results of experiments indicate that the streaming rate $q$ and the level limit $l$ have an impact on both the overall streaming cost and the network cost. The results of numerical experiments showed that the additional cost required in the network to introduce extra survivability constraints is relatively small, i.e., for FA problem it was 22.8, 34.3 and 33.3 % for link, node and ISP disjoint multicast trees, respectively and for CFA those values were even lower—5, 5.5 and 6.8 % correspondingly.

For future work, we are planning to develop, implement, and test heuristic algorithms for the CFA problem including constructive algorithms as well as metaheuristic approaches like Tabu Search and Simulated Annealing That should enable us to examine dual homing survivability for networks much larger than 10 hosts.