Abstract
The use of Aloha-based random access protocols is interesting when channel sensing is either not possible or not convenient and the traffic from terminals is unpredictable and sporadic. In this paper an analytic model for packet interference calculation in asynchronous random access protocols using diversity is presented. The aim is to provide a tool that avoids time-consuming simulations to evaluate packet loss and throughput in case decodability is still possible when a certain interference threshold is not exceeded. Moreover the same model represents the groundbase for further studies in which iterative interference cancellation is applied to received frames.






Similar content being viewed by others
Notes
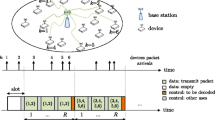
In this work all burst durations are assumed to be equal.
With the term normalized MAC channel load we refer to the load generated from different packets regardless of the number of copies generated for each packet.
As claimed in [9], even though this threshold is quite optimistic it can be considered valid for moderate to high SNIR. Nevertheless the developed model can be easily adapted by simply substituting a different value for the threshold.
References
Yue, W., & Matsumoto, Y. (2000). Output and delay of multi-channel slotted ALOHA systems for integrated voice and data transmission. Telecommunication Systems, 13(2–4), 147–165.
Tian, X., Chen, X., Ideguchi, T., & Okuda, T. (2008). Improving protocol capacity by scheduling random access on WLANs. Telecommunication Systems, 37(1–3), 19–28.
Del Rio Herrero, O., & De Gaudenzi, R. (2008). A high efficiency scheme for quasi-real-time satellite mobile messaging systems. In Proceedings of 10th international workshop on signal processing for space communications (SPSC), 1–9.
Meloni, A., & Murroni, M. (2014). Random Access in DVB-RCS2: Design and dynamic control for congestion avoidance. IEEE Transactions on Broadcasting, 60(1), 16–28. doi:10.1109/TBC.2013.2293920.
Abramson, N. (1970). The Aloha system: Another alternative for computer communications. In Proceedings of the 1970, fall joint computer Conference, AFIPS Conference. 37, 281–285.
Roberts, L.G. (1972). ALOHA packet systems with and without slots and capture. ARPANET System Note 8 (NIC11290).
Choudhury, G. L., & Rappaport, S. S. (1983). Diversity ALOHA - A random access scheme for satellite communications. IEEE Transactions on Communications, 31, 450–457.
Casini, E., De Gaudenzi, R., & del Rio, Herrero O. (2007). Contention resolution dversity slotted ALOHA (CRDSA): An enhanced random access Schemefor satellite access packet networks. IEEE Transactions on Wireless Communications, 6(4), 1408–1419.
Kissling, C. (2011). Performance enhancements for asynchronous random access protocols over satellite. In IEEE international conference on communications (ICC), 1–6.
Clazzer, F., & Kissling, C. (2013). Enhanced contention resolution Aloha—ECRA. In Proceedings of the 9th international ITG conference on systems, communications and coding (SCC).
Meloni, A., & Murroni, M. (2013). On the stability of asynchronous random access schemes. In Proceedings of the 9th international wireless communications and mobile computing conference (IWCMC), 843–848.
Liva, G. (2011). Graph-based analysis and optimization of contention resolution diversity slotted ALOHA. IEEE Transactions on Communications, 59(2), 477–487.
Kumar, A., & Patil, D. (1997). Stability and throughput analysis of unslotted CDMA-ALOHA with finite number of users and code sharing. Telecommunication Systems, 8(2–4), 257–275.
Meloni, A., & Murroni, M. (2012). CRDSA, CRDSA++ and IRSA: Stability and performance evaluation. In Proceedings of advanced satellite multimedia systems conference (ASMS) and 12th signal processing for space communications workshop (SPSC), 220–225.
Lauwens, B., Scheers, B., & Capelle, A. (2010). Performance analysis of unslotted CSMA/CA in wireless networks. Telecommunication Systems, 44(1–2), 109–123.
Zorzi, M. (1995). Mobile radio slotted ALOHA with capture and diversity. Wireless Networks, 1(2), 227–239.
Meloni, A., & Murroni, M. (2013). Average Power Limitations in Sliding Window Contention Resolution Diversity Slotted Aloha. In Proceedins of the 9th international wireless communications and mobile computing conference (IWCMC), 7–12.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this section, the validity of the interference model is proven by demonstrating that the sum of all contributions is equal to 1. For simplicity, the demonstration is cut in four parts, each corresponding to the probability that the first event was (A), (B), (C) or (D) respectively and considering the union of the events for the second DP’s copy. Therefore
Any of the four terms are thoroughly discussed in the followings.
-
(i)
$$\begin{aligned} Pr\{(A,CD)_{\tau '}\}=\frac{1}{T_F'-\tau '+1} \end{aligned}$$(30)
represents the case in which the first copy of the DP entirely interfered with the CC. In this case, the two possible events for the second DP’s copy are (C) and (D). This quantity has already been calculated and explained in Eq. (13).
-
(ii)
$$\begin{aligned}&\sum _{x'=1}^{\tau '}Pr\{(B,BCD)_{x'}\} = Pr\{(B,B)_{\tau '}\} \nonumber \\&\quad +\sum _{x'=1}^{\tau '-1}Pr\{(B,CD)_{x'}\} +\sum _{x'=1}^{\tau '-1}Pr\{(B,B)_{x'}\} \end{aligned}$$(31)
represents the case in which the first copy of the DP partially interfered with the CC. In this case, the possible events for the second DP’s copy are three: (B), (C) and (D). Substituting the values from Eqs. (17), (19), (20) and considering the common factors
$$\begin{aligned}&\sum _{x'=1}^{\tau '}Pr\{(B,BCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{T_F'-\tau '+1}\cdot \frac{2}{T_F'-\tau '+1-(2\tau '-1)}\Bigg ] \nonumber \\&\qquad \cdot \Bigg [(\tau '-1) \!+\! \sum _{x'=1}^{\tau '-1} \big [T_F'-\tau '+1-(2\tau '-1)-(\tau '-x')\big ] \nonumber \\&\qquad +\sum _{x'=1}^{\tau '-1} (x'-1)\Bigg ] \end{aligned}$$(32)that can be rewritten as
$$\begin{aligned}&\sum _{x'=1}^{\tau '}Pr\{(B,BCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{T_F'-\tau '+1}\cdot \frac{2}{T_F'-\tau '+1-(2\tau '-1)}\Bigg ]\cdot \nonumber \\&\qquad \left[ (\tau '-1) + (\tau '-1)\cdot \left[ T_F'-\tau '+1-(2\tau '-1)\right] \right. \nonumber \\&\qquad \left. -\sum _{x'=1}^{\tau '-1}(\tau '-x') + \sum _{x'=1}^{\tau '-1} (x'-1)\right] \end{aligned}$$(33)Considering that
$$\begin{aligned} -\sum _{x'=1}^{\tau '-1}(\tau '-x')=-(\tau '-1)-\sum _{x'=1}^{\tau '-1} (x'-1) \end{aligned}$$(34)Equation (36) becomes
$$\begin{aligned}&\sum _{x'=1}^{\tau '}Pr\{(B,BCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{T_F'-\tau '+1}\cdot \frac{2}{T_F'-\tau '+1-(2\tau '-1)}\Bigg ]\cdot \nonumber \\&\qquad \times \Bigg [(\tau '-1)\cdot [T_F'-\tau '+1-(2\tau '-1)]\Bigg ] \end{aligned}$$(35)Therefore
$$\begin{aligned} \sum _{x'=1}^{\tau '}Pr\{(B,BCD)_{x'}\}=\frac{2(\tau '-1)}{T_F'-\tau '+1} \end{aligned}$$(36) -
(iii)
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(C,ABCD)_{x'\}} = Pr\{(C,A)_{\tau '}\} \nonumber \\&\quad + \sum _{x'=1}^{\tau '-1}Pr\{(C,B)_{x'}\} +Pr\{(C,CD)_{0}\} \end{aligned}$$(37)
represents the case in which the first copy of the DP did not interfere with the CC and did not change the number of possible interference outcomes. In this case, the possible events for the second DP’s copy are still four: (A), (B), (C) and (D). Substituting the values from Eqs. (16), (21), (24) and considering the common factors
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(C,ABCD)_{x'\}} = \Bigg [\frac{T_F'-\tau '+1-(4\tau '-1)}{T_F'-\tau '+1}\Bigg ] \nonumber \\&\cdot \Bigg [\frac{1+\sum _{x'=1}^{\tau '-1}2+[T_F'-\tau '+1-2(2\tau '-1)]}{T_F'-\tau '+1-(2\tau '-1)}\Bigg ] \end{aligned}$$(38)With some simple mathematical passages it can be seen that the term on the second big square brackets equals \(1\), therefore
$$\begin{aligned} \sum _{x'=0}^{\tau '}Pr\{(C,ABCD)_{x'\}}=\frac{T_F'-\tau '+1-(4\tau '-1)}{T_F'-\tau '+1}\nonumber \\ \end{aligned}$$(39) -
(iv)
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(D,ABCD)_{x'}\} = Pr\{(D,A)_{\tau '}\} \nonumber \\&\quad + \sum _{x'=1}^{\tau '-1}Pr\{(D,B)_x'\} + Pr\{(D,CD)_0\} \end{aligned}$$(40)
represents the case in which the first copy of the DP did not interfere with the CC but the number of possible interference outcomes is modified. In this case, the possible events for the second DP’s copy are (A), (B), (C) and (D). Substituting the values gathered from Eqs. (16), (22), (25) and considering the common factors
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(D,ABCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{[T_F'-\tau '+1]\cdot [T_F'-\tau '+1-(2\tau '-1)]}\Bigg ] \nonumber \\&\qquad \cdot \left[ 2\tau ' + \sum _{x'=1}^{\tau '-1} 2x' + \sum _{x'=1}^{\tau '-1} 4(\tau '-x')\right. \nonumber \\&\qquad \left. \quad + \sum _{x'=1}^{\tau '-1} 2[T_F'-\tau '+1-(3\tau '+x'-1)]\right] \end{aligned}$$(41)Considering that
$$\begin{aligned} \sum _{x'=1}^{\tau '-1} x' = \sum _{x'=1}^{\tau '-1} (\tau '-x') = \frac{(\tau ')\cdot (\tau '-1)}{2} \end{aligned}$$(42)Equation (41) can be rewritten as
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(D,ABCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{[T_F'-\tau '+1]\cdot [T_F'-\tau '+1-(2\tau '-1)]}\Bigg ]\cdot \nonumber \\&\qquad \left[ 2\tau ' +2\frac{(\tau ')\cdot (\tau '-1)}{2} + 4\frac{(\tau ')\cdot (\tau '-1)}{2} \right. \nonumber \\&\qquad \left. +\,2\tau '\cdot [T_F'-\tau '+1-(3\tau '-1)] - 2\frac{(\tau ')\cdot (\tau '-1)}{2}\right] \nonumber \\ \end{aligned}$$(43)from which
$$\begin{aligned}&\sum _{x'=0}^{\tau '}Pr\{(D,ABCD)_{x'}\} \nonumber \\&\quad = \Bigg [\frac{1}{[T_F'-\tau '+1]\cdot [T_F'-\tau '+1-(2\tau '-1)]}\Bigg ]\cdot \nonumber \\&\qquad \times \Bigg [2\tau ' \cdot [T_F'-\tau '+1-(2\tau '-1)]\Bigg ] \end{aligned}$$(44)and simplifying
$$\begin{aligned} \sum _{x'=0}^{\tau '}Pr\{(D,ABCD)_{x'}\}=\frac{2\tau '}{T_F'-\tau '+1} \end{aligned}$$(45)
It can be seen that the sum of the terms found in Eqs. (30),(36),(39) and (45) is equal to 1. This validates Eq. (29).
Rights and permissions
About this article
Cite this article
Meloni, A., Murroni, M. Interference calculation in asynchronous random access protocols using diversity. Telecommun Syst 63, 45–53 (2016). https://doi.org/10.1007/s11235-015-9970-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11235-015-9970-3