Is the conjunction fallacy tied to probabilistic confirmation?

Abstract

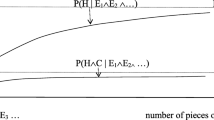
Crupi et al. (2008) offer a confirmation-theoretic, Bayesian account of the conjunction fallacy—an error in reasoning that occurs when subjects judge that Pr(h ₁ & h ₂|e) > Pr(h ₁|e). They introduce three formal conditions that are satisfied by classical conjunction fallacy cases, and they show that these same conditions imply that h ₁ & h ₂ is confirmed by e to a greater extent than is h ₁ alone. Consequently, they suggest that people are tracking this confirmation relation when they commit conjunction fallacies. I offer three experiments testing the merits of Crupi et al.’s account specifically and confirmation-theoretic accounts of the conjunction fallacy more generally. The results of Experiment 1 show that, although Crupi et al.’s conditions do seem to be causally linked to the conjunction fallacy, they are not necessary for it; there exist cases that do not meet their three conditions in which subjects still tend to commit the fallacy. The results of Experiments 2 and 3 show that Crupi et al.’s conditions, and those offered by other confirmation-theoretic accounts of the fallacy, are not sufficient for the fallacy either; there exist cases that meet all three of CFT’s conditions in which subjects do not tend to commit the fallacy. Additionally, these latter experiments show that such confirmation-theoretic conditions are at best only weakly causally relevant to the presence of the conjunction fallacy. Given these findings, CFT’s account specifically, and any general confirmation-theoretic account more broadly, falls short of offering a satisfying explanation of the presence of the conjunction fallacy.