APPLE: approximate path for penalized likelihood estimators

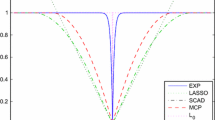
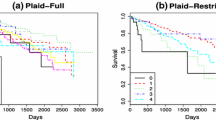
Abstract

In high-dimensional data analysis, penalized likelihood estimators are shown to provide superior results in both variable selection and parameter estimation. A new algorithm, APPLE, is proposed for calculating the Approximate Path for Penalized Likelihood Estimators. Both convex penalties (such as LASSO) and folded concave penalties (such as MCP) are considered. APPLE efficiently computes the solution path for the penalized likelihood estimator using a hybrid of the modified predictor-corrector method and the coordinate-descent algorithm. APPLE is compared with several well-known packages via simulation and analysis of two gene expression data sets.

Appendices

Appendix A: Logistic regression

1.1 A.1 LASSO

In logistic regression, we assume (x _i , y _i ), i=1,…,n are i.i.d. with $\mathbb{P}(y_{i}=1|\boldsymbol{x}_{i})=p_{i}=\exp(\boldsymbol{\beta}'\boldsymbol{x}_{i})/(1+\exp(\boldsymbol{\beta}'\boldsymbol{x}_{i}))$. Then the target function for the LASSO penalized logistic regression is defined as

The KKT conditions are given as follows.

We define active set A _k as

$$A_k=\bigg\{j: \bigg|\frac{1}{n}\sum_{i=1}^n \biggl\{y_i-\frac{\exp({\widehat {\boldsymbol{\beta}}}^{(k)'} \boldsymbol{x}_i)}{1+\exp({\widehat {\boldsymbol{\beta}}}^{(k)'}\boldsymbol{x}_i)}\biggr\}x_{ij}\bigg|\ge \lambda_k \bigg\} \cup \{0\}. $$

To update, we define

(11)

then $\boldsymbol{s}^{(k)} = (0, \boldsymbol{s}^{(k)'}_{-0})'$, $\boldsymbol{d}^{(k)} = (0, \boldsymbol{d}^{(k)'}_{-0})'$, where

To correct,

1.2 A.2 MCP

For MCP penalized logistic regression, we define the target function as

The KKT conditions are given as follows.

For a given λ _k , define the active set A _k as

$$A_k=\{A_{k-1}\cup N_k\}\setminus D_k, $$

where

and

To perform adaptive rescaling on γ, define

To update, the derivatives are defined as follows,

(12)

(13)

(14)

(15)

and

To correct we use

$${\widehat {\boldsymbol{\beta}}}^{(k,j+1)}_{A_k}={\widehat {\boldsymbol{\beta}}}^{(k,j)}_{A_k}-\bigg(\frac{\partial^2 L^{(k)}}{\partial \boldsymbol{\beta}_{A_k}\partial \boldsymbol{\beta}_{A_k}^T}\bigg)^{-1} \bigg(\frac{\partial L^{(k)}}{\partial \boldsymbol{\beta}_{A_k}}\bigg), $$

where

(16)

(17)

and

(18)

Appendix B: Poisson regression

2.1 B.3 LASSO

In Poisson regression, we assume (x _i , y _i ), i=1,…,n are iid with $\mathbb{P}(Y=y_{i})=e^{-\lambda_{i}}\lambda_{i}^{y_{i}}/(y_{i})!$, where logλ _i =β′x _i . Then criterion for the LASSO penalized Poisson regression is defined as

$$L(\boldsymbol{\beta})=\frac{1}{n}\sum_{i=1}^n \big\{\exp(\boldsymbol{\beta}'\boldsymbol{x}_i)-y_i(\boldsymbol{\beta}'\boldsymbol{x}_i)\big\}+\lambda\sum_{j=1}^p |\beta_j|. $$

The KKT conditions are given as follows.

For a given λ _k , we define the active set A _k as follows.

$$A_k=\Biggl\{j:~ \Bigg|\frac{1}{n}\sum_{i=1}^n \{y_i-\exp({\widehat {\boldsymbol{\beta}}}^{(k)'}\boldsymbol{x}_i)x_{ij}\}\Bigg|\ge \lambda_k\Biggr\}\cup \{0\}. $$

To update, we define

then

and

To correct,

2.2 B.4 MCP

For MCP penalized Poisson regression, we define the target function as

The KKT conditions are,

For a given λ _k , the active set is defined as

$$A_k=\{A_{k-1}\cup N_k\}\setminus D_k, $$

where

and

To update, the derivatives are defined as follows,

and

To correct we use

where

(19)

(20)

and

(21)